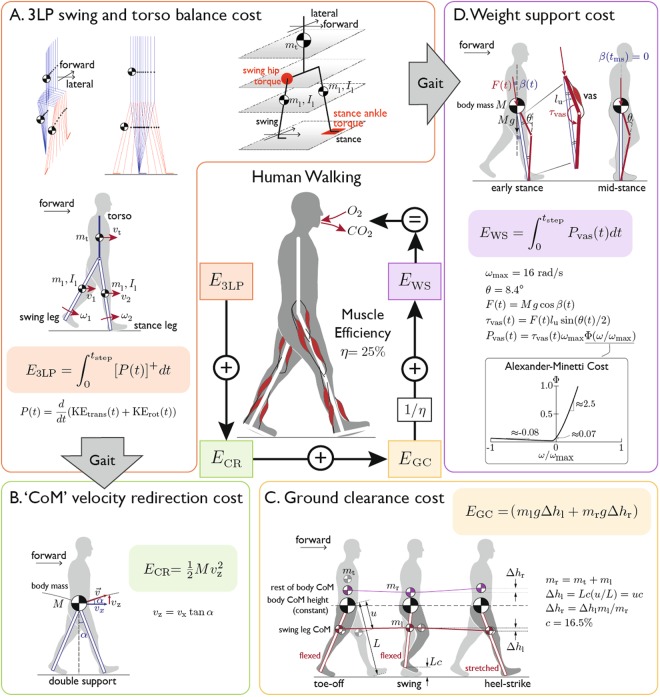
Figure 3.

The four energy components of the metabolic cost model and their formulations. The cost components are from (A) 3LP dynamics, (B) CoM velocity redirection, (C) ground clearance, and (D) weight support. (A) 3LP is composed of three linear pendulums (blue), two represent the legs and one for the trunk. Translational and rotational kinetic energies are calculated from the linear and angular velocities of each segment. The 3LP cost is the integral of the positive component of the kinetic energy change rate. (B) CoM velocity redirection cost accounts for the vertical work to change CoM velocity at the step-to-step transitions, which is not accounted for by the 3LP model. Similar to Kuo⁴⁸, the magnitude of the velocity redirection, and thus kinetic energy, depends on geometry (i.e. the angle α between the legs). This angle comes from 3LP geometry (represented in blue). (C) Ground clearance cost is the potential energy to lift the leg. We used a constant c of 16.5% of leg length for lift height. Since the vertical CoM displacement must be constant, there is a corresponding penalty to move the ‘rest of body’ mass down. (D) Supporting the body during stance requires extensor muscular force to keep the leg from collapsing. The metabolic cost of the vasti muscles performing leg extension is calculated from the Alexander-Minetti curve⁵², following the work of Srinivasan⁵¹. The leg angle β(t) is derived from 3LP geometry (blue), and we used a constant knee angle θ of 8.4 degrees.