Temporal Dynamics of Hippocampal and Medial Prefrontal Cortex Interactions During the Delay Period of a Working Memory-Guided Foraging Task

Abstract

Connections between the hippocampus (HC) and medial prefrontal cortex (mPFC) are critical for working memory; however, the precise contribution of this pathway is a matter of debate. One suggestion is that it may stabilize retrospective memories of recently encountered task-relevant information. Alternatively, it may be involved in encoding prospective memories, or the internal representation of future goals. To explore these possibilities, simultaneous extracellular recordings were made from mPFC and HC of rats performing the delayed spatial win-shift on a radial maze. Each trial consisted of a training-phase (when 4 randomly chosen arms were open) and test phase (all 8 arms were open but only previously blocked arms contained food) separated by a 60-s delay. Theta power was highest during the delay, and mPFC units were more likely to become entrained to hippocampal theta as the delay progressed. Training and test phase performance were accurately predicted by a linear classifier, and there was a transition in classification for training-phase to test-phase activity patterns throughout the delay on trials where the rats performed well. These data suggest that the HC and mPFC become more strongly synchronized as mPFC circuits preferentially shift from encoding retrospective to prospective information.

Introduction

Working memory is characterized by the ability to transiently maintain and manipulate information used to guide a forthcoming response (Baddeley and Hitch 1974). Working memory tasks typically consist of 3 phases; an initial training-phase where task-relevant information is sampled, a delay phase where the information is transiently retained and/or manipulated, and a final test/response phase where previously acquired information is used to guide a forthcoming response. Increases in neural firing in prefrontal cortex (PFC) during the delay period of these tasks have been interpreted as the neural basis for the transient storage of a mnemonic trace necessary to guide behavior (Goldman-Rakic 1996; Funahashi 2015). However, other explanations for this delay-period activity have been advanced (Tsujimoto and Postle 2012; Lara and Wallis 2015), including the suggestion that these firing patterns may be involved in the allocation of cognitive resources through the monitoring and selection of task-relevant representations in other brain regions (Curtis and D'Esposito 2003; Postle 2006). Accordingly, activity in PFC is critical for the maintenance of mnemonic and spatial representations in posterior parietal cortex or hippocampus (HC) (Chaffe and Goldman-Rakic 2000; Kyd and Bilkey 2003; Harvey et al. 2012).

Two cognitive strategies have been implicated in the efficient allocation of cognitive resources throughout a delay. The first is a retrospective strategy by which subjects retain a memory of previously acquired information that can subsequently be used to deduce the correct action during test/response phase, while the second is a prospective strategy where subjects formulate a future action plan and maintain it throughout the delay (Cook et al. 1985). These separate strategies appear to involve common neural circuits, including the PFC and HC in humans (Mok 2012; Brown et al. 2016) and rats (Kesner 1989; Floresco et al. 1997; Ferbinteanu and Shapiro 2003; Churchwell and Kesner 2011; Horst and Laubach 2012; Han et al. 2013). Furthermore, neurophysiological data are consistent with both retrospective and prospective code in the 2 regions as the persistent delay-period activity in the rat and primate PFC contains information about previously presented stimuli as well as anticipated stimuli, goals, or actions (Rainer et al. 1999; Watanabe and Funahashi 2004; Luk and Wallis 2009; Horst and Laubach 2012; Hyman et al. 2013; Matsushima and Tanaka 2013). Likewise, rat hippocampal place cells “replay” past maze locations (Louie and Wilson 2001; Foster and Wilson 2006; Karlsson and Frank 2009) and fire in anticipation of future choice trajectories (Ferbinteanu and Shapiro 2003; Itskov et al. 2008; Pfeiffer and Foster 2013; Catanese et al. 2014; Redish 2016). Neurons in the rat mPFC also represent future trajectories on a maze (Ito et al. 2015) suggesting that prospective coding of spatial locations may be simultaneously maintained in both regions.

Information transfer between the HC and mPFC is likely to require synchronized neural activity, especially in the theta-band. Theta-band coherence and entrainment of mPFC firing to HC theta oscillations (~7–8 Hz; phase-locking) is enhanced during the delay and choice periods of working memory tasks (Johnson et al. 2007; Hyman et al. 2010; Jadhav et al. 2012; Hallock et al. 2016). It has been argued that this type of entrainment may mainly subserve a retrospective memory function, acting to stabilize mnemonic representations in cortex (Colom et al. 1988; Paré and Gaudreau 1996; Frank et al. 2001; Berke et al. 2004; Siapas et al. 2005; Kayser et al. 2009). Alternatively, other data are more consistent with a prospective coding function as rat mPFC neurons exhibit robust phase-locking to HC rhythms during choice epochs just prior to the initiation of responses (Johnson et al. 2007; Hyman et al. 2010), which coincides with prospective activity in hippocampal place cells (Johnson et al. 2007), therefore, suggesting a prospective role. Likewise, in humans, the covariance of HC and PFC activity is associated with the representation of future goal locations (Bähner et al. 2015; Brown et al. 2016). While HC–mPFC interactions have been implicated in both retrospective and prospective memory functions, the question of how retrospective versus prospective information is parsed and dynamically transferred between the areas is unknown.

In the present study, rats were implanted with arrays of electrodes in both the dorsal HC and the anterior cingulate cortex (ACC) portion of the mPFC, and the temporal dynamics of the interactions across these brain regions were analyzed during the performance of a delayed spatial win-shift (DSWS) task on a radial arm maze. The DSWS task was chosen because the memory load required to complete the task is high and retrospective and prospective strategies act to help reduce the load at different points during the task. Although seeking equivalence between frontal cortical areas among mammalian species is “unrealistic” (Passingham and Wise 2012), the rat mPFC does appear to exhibit certain aspects of functional homology with both the ACC and dorsolateral PFC of primates (Seamans et al. 2008). On this task, inactivation of the connection between the HC and mPFC severely disrupts performance (Floresco et al. 1997). Here, we assessed how HC rhythms interacted with the activity of mPFC neurons during the delay period of the DSWS and evaluated whether information carried by this pathway during the delay period was more consistent with a retrospective versus prospective memory code.

Materials and Methods

Behavior and Recordings

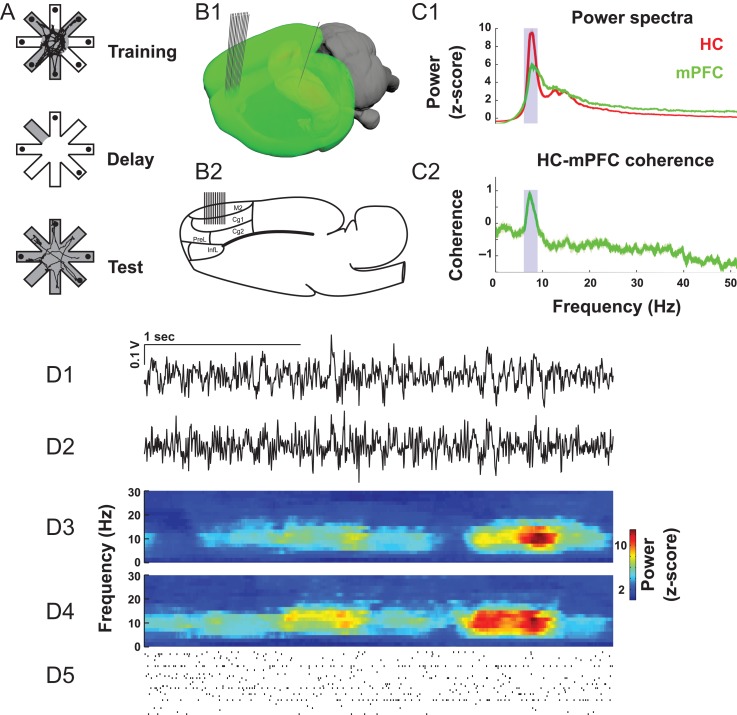
Data acquisition and behavioral assessments were performed as previously described (Lapish et al. 2008). Animals were treated in accordance with the ethical guidelines endorsed by the University of British Columbia and Canadian Council for Animal Care. Briefly, the DSWS consisted of 3 phases (Fig. 1A). Prior to the start of a trial, 4 arms were randomly selected and baited with 125 μl of chocolate milk placed in plastic food cups located at the ends of the arms. The remaining 4 arms were blocked by removable doors. Configurations containing 3 or more adjacent open or blocked arms were never used. In the first phase of the task, known as the training-phase, the animals collected the rewards from the 4 open arms. Upon visiting the last baited arm, the arm door closed behind the animal locking them in this arm for the ensuing 60- to 90-s “delay” phase with the room lights extinguished. After the delay phase, the room lights were illuminated and the “test phase” commenced. In the test phase, all arms were open but only those previously blocked during the training-phase contained chocolate milk reward.

Figure 1.

Task description and examples of theta-band activity. (A) In the DSWS task, 4 of the 8 maze arms are open during the training-phase. After all available rewards are consumed, and after a 60–90 s delay, the previously blocked arms are opened during the test phase. (B) 24 single wires were implanted in mPFC and one LFP electrode in HC. (C) Both mPFC and HC field potentials feature a strong peak in theta-band (blue shading) power (C1) and coherence (C2). (D) Example LFPs (D1, D2), time-frequency decompositions (D3, D4), and spike trains (D5).

After performing the task for 2 consecutive days with 1 error or less, rats were implanted with the recording arrays. In total, 5 male Long–Evans rats had static 2 × 12 arrays of single electrodes (diameter = 25 μm, impedance = 150–300 kOhm, California Fine Wire) implanted into the mPFC spanning 1.8 mm of anterior–posterior axis of the structure Cg1 field (A/P 2.2 mm, M/L 0.8 mm, D/V 2.5 mm to bregma and offset 10° from the vertical). A single electrode was also implanted in dorsal HC CA1 field (AP −3.6 mm, ML 2.0 mm, DV −2.5 mm). This location was chosen to be consistent with previous studies of HC-PFC synchrony (Jones and Wilson 2005; Siapas et al. 2005; Hyman et al. 2010) as well as in accordance with data indicating a stronger association of dorsal HC function with cognitive processing (Fanselow and Dong 2010).

After recovery, the arrays were connected via a pre-amplifer headstage, tether and commutator to Lynx 8 amplifiers and a Neuralynx Cheetah 32 channel recording system (Neuralynx). Voltage data were sampled at 30 303 Hz and amplified 10 000×. The mPFC electrode with the least spiking activity was selected for LFP recordings and referenced to a distal ground screw placed posterior to lambda. The remaining electrodes were referenced locally. The threshold for spike detection was set to 50 μV, which corresponded to ~5× of the RMS portion of the voltage signal. The movement of the animal on the maze was detected via image processing software (Noldus EthoVision) that captured the center of mass of the animal in x–y coordinates and transferred this information via voltage signals fed directly into the Neuralynx recording system. Movement data were sampled at 6 Hz.

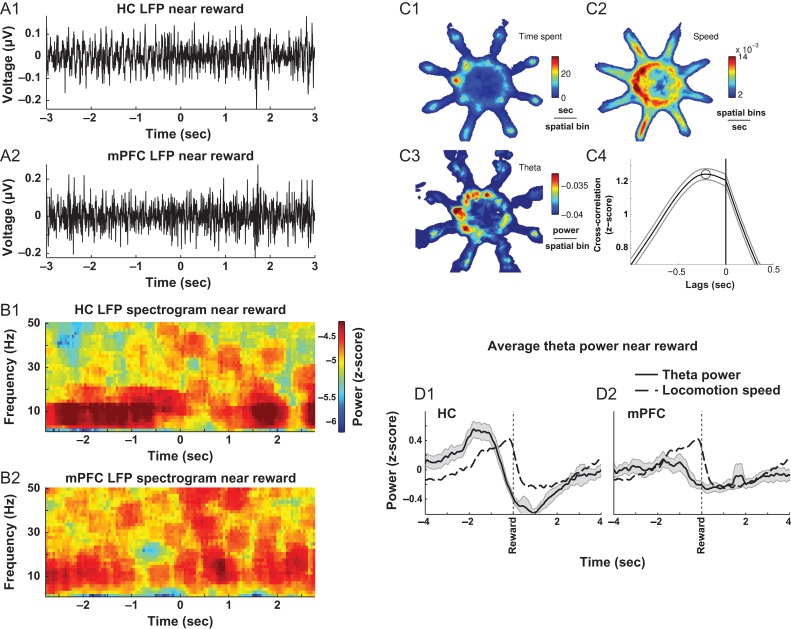
All behavior was analyzed offline. The “reward time” was defined as the latency to travel from an arm door threshold (i.e., the corner between the center platform and the arm) to the reward cup at the end of the arm (Fig. 2C1). Movement velocity was calculated as Euclidean distance between adjacent coordinates of the rat location in Cartesian space per second (Fig. 2C2). Errors during the test phase were defined as any entry into arms visited previously during the training-phase or any arm re-entry during the test phase (Seamans et al. 1995). In order to examine the factors associated with poor performance on the maze, trials were split into those with poor versus good performance. Trials on which rats made 3 or more errors during the test phase or trials in which the combined duration of training and test phases exceeded 5 min were classified as poor performance trials (Lapish et al. 2015). Twenty-seven of 48 trials were classified as good performance trials (3 from rat 1, 5 from rat 2, 7 from rat 3, 7 from rat 4, and 5 from rat 5), whereas the remaining were classified as poor performance trials (9 from rat 1, 1 from rat 2, 3 from rat 3, 4 from rat 4, and 4 from rat 5).

Figure 2.

Theta power increases during putative choice epochs and precedes peak in movement velocity. (A) Sample hippocampal (A1) and mPFC (A2) LFP traces where increases in theta oscillation are observed immediately prior to obtaining a reward (−2–0 s). (B) Time-frequency decomposition of traces in (A). (C) Average spatial representation of time spent in a given location on the maze (C1), the running speed at a given location on the maze (C2), HC power in the theta-band is highest near arm entrances, while velocity is frequently elevated inside arms when approaching reward locations (C3). Theta-velocity cross-correlation suggests that during the 8-s window surrounding reward acquisition, peak in theta precedes the peak in velocity by ~0.21 s (dashed line in C4; mean ± 95% confidence interval). (D) Changes in theta power and movement velocity measured during putative “choice” epochs preceding reward in the HC (D1) and mPFC (D2) (mean ± 95% confidence interval).

Analysis of Neural Activity

Summary

Briefly, raw neural recordings were split into 2 analysis pipelines. In one pipeline, spikes were extracted to obtain timelines of activation for individual single units. In the other pipeline, raw data were down-sampled, detrended, and denoised to obtain the local field potential signals. Multitaper spectrograms were constructed to quantify the power of theta oscillation, and the phase of theta at the times of spikes was collected to quantify phase-locking.

Spike Sorting and Denoising

Spikes were sorted offline using a combination of principal component analysis (PCA), wavelet, and spike characterization features using Simpleclust software (github.com/open-ephys/simpleclust). Since we used single wire electrodes, only well-isolated single units were included in the analysis. To obtain local field potentials, raw data were down-sampled by decimation to 6000 Hz and filtered using inverse fast Fourier transform to remove line noise at 60, 120, and 180 Hz ± 2 Hz (Zanos et al. 2011). Finally, a running line fit was subtracted from data denoised in this manner using local linear regression with a moving window of 100 ms and step of 5 ms (Mitra and Bokil 2007) in order to remove any slow changes in voltage that could affect the estimation of theta phase and power. These steps were performed to ensure that the signal used for estimation of phase and power was as free of artifacts or noise.

Spectral Analysis

For spectral analyses including power and coherence, multitaper decomposition was applied to detrended and denoised data using 5 tapers and time-bandwith product of 3 using the “chronux” software package for MATLAB (Mitra and Bokil 2007). A moving window with a width of 10 s and a 0.2 s step was used for extraction of theta-band components between 7 and 8.5 Hz, which matched the observed theta peak in HC and mPFC spectra (Fig. 1C1–2), as well as coherence (black horizontal lines, Fig. 3A–D). Two-dimensional histograms of average theta and running speed were smoothed for plotting using 2-dimensional splines (Fig. 2C1–3) (Garcia 2010). The relationship between movement velocity and theta power (Fig. 2C4) was examined on data from all experiments excluding one outlier (n = 51) by computing the autocorrelation normalized cross-correlation via the “xcorr” function in MATLAB. The mean power in these frequency bands was used as a measure of theta power over time. To standardize the amount of time included in the analyses across data sets, each analysis was restricted to the shortest amount of time (across all animals) taken to complete the training or test phase (13.5 s). Inclusion of all the data did not change the pattern of theta power (not shown). Bins in which overall power exceeded 2.5 standard deviations of mean values, possibly indicating transient movement-related noise, were excluded. Comparisons of power and coherence by task-phase were based on mean values of z-scored theta multitaper values over the entire epochs, and were analyzed across task phases by repeated measures ANOVA. In order to track long-term changes in theta power throughout delay periods, the delay theta-band LFP power was divided into 1-s bins. Slopes of changes of power across the delay were quantified using linear regression.

Figure 3.

Robust increases in theta-band power and coherence are observed on good performance trials. (A–C) Average spectrograms and coherence during a period of time including delay and ~10 s of the training and test phases. Theta power and coherence are maximal during second half of delay. (D) Left and center, theta power and coherence are low during training and first half of delay and high during second half of delay and test phases. Right, HC–mPFC coherence is highest during the second half of delay (Tukey's multiple-comparisons test, *P < 0.05, **P < 0.01, ***P < 0.001). (E) Theta power during all trials shows a gradual increase from beginning to end of delay in good (E1) but not poor (E2) performance trials. (F) Average z-scored theta power increases gradually during delay. (G) Theta power slopes are lower in poor performance trials, indicating that an optimal foraging strategy is associated with more robust increases in theta power across the delay.

Phase-Locking

For phase analysis, field potentials were filtered between 5 and 10 Hz using a forward and reverse Parks–McClellan finite impulse response filter in order to preserve theta wave shape (Siapas et al. 2005). Arctangent of the real and imaginary parts of Hilbert transform provided instantaneous phase information with 6 kHz resolution, and the instantaneous phases were collected at the times when spikes occurred. Phase-locking was quantified by computing Rayleigh's Z statistic and the associated P-value (Berens 2009). First, significantly entrained units (P < 0.05) were identified using data from the entire delay period. Then, Rayleigh's Z statistic was computed for the first and last 30 s of the delay period on these units as follows: $Z=\frac{{\left(nR\right)}^2}{n}$, where n is the number of spikes and R is the resultant vector length of theta angles, $R=\frac{\left|\sum \left(w^{⁎}\exp \left(i\mathrm{\alpha }\right)\right)\right|}{\sum w}$, where w is number of incidences of angles, α.

Principal Components Analysis

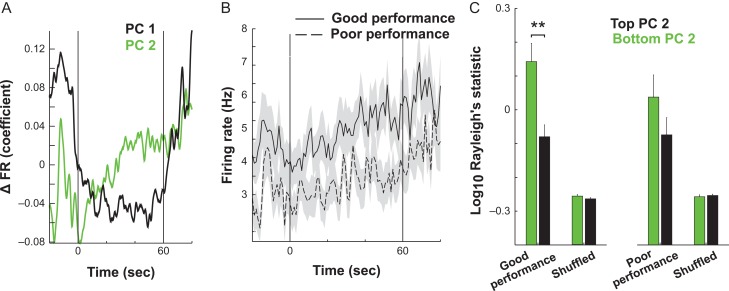
In order to identify the main patterns of firing rate variance across the delay, the task was subdivided into the last 20 s of the training-phase, the entire delay period, and the initial 20 s of the test phase. These periods were then separated into 1 ms bins and each bin was assigned either a value of one if it contained a spike or a 0 if it did not. This binary spike count vector for each neuron was then convolved with a Gaussian kernel having a standard deviation of 100 ms. Convolved spike count vectors from all neurons within a trial were then combined and subjected to PCA. PC1 and 2 captured the main patterns of firing rate variance across the neurons through time. Neurons most strongly exhibiting PC1 and PC 2 firing rate patterns were identified as those expressing absolute loadings on PCs 1 and 2 that were in the top 33% of the population. Phase-locking of these neurons was analyzed separately from the rest of the population and these data are presented in Figure 5C1 and C2. For comparison of broad firing rate trends in PC 2-affiliated units during delay in good and poor performance trials (Fig. 5B), spike times were binned at 1 s and subjected to a repeated measures ANOVA. A baseline estimate of how much phase-locking would be expected by chance was achieved by shifting spike trains in a circular manner at a random time intervals and repeating the phase-locking analyses 100 times for every unit.

Figure 5.

During good performance trials, a subpopulation of mPFC units transition to a reconfigured, theta-dominated state during delay. (A) The neural activity pattern captured by the first PC identified neurons that decrease firing during the delay (black line, −20–0 s and 60–80 s). In contrast, another activity pattern was identified by PC 2 that initially decline at the onset of delay (0 s) and then continuously increased until the second half of delay (~30 s). (B) Neurons were split by task performance, and firing rates were quantified in neurons that most heavily loaded onto PC 2, revealing a performance × time interaction. This indicates that increases in firing in PC 2-associated neurons are most robust on good performance trials. (C). Units that most heavily load onto PC 2 are more entrained to theta than those that load most weakly. This distinction is not evident in poor performance trials (main effect of PC, Tukey multiple-comparisons test, P < 0.01), thus indicating that the emergence of phase-locking in this neural population is important for task performance. Data in B and C are presented as mean ± SEM.

Decoding

To determine whether ensemble activity during the delay period represented information about past training-phase choices (i.e., retrospective coding) or forthcoming test-phase choices (i.e., prospective coding), the following decoding analyses were employed. Spike trains across the entire trial were first binned at 1 ms and convolved with a Gaussian kernel with a standard deviation of 50 ms. The decreased bandwidth of the Gaussian kernel relative to the previous analysis was chosen in order to detect faster changes in the neural trajectories. The spike count vector for each neuron formed a single axis of a multiple single-unit activity (MSUA) space and each point in this MSUA space represented the spike count values of all neurons during a single 1 s time bin of the task. Time bins were then assigned to one of 2 classes depending on whether they were extracted from the training (class 1) or the test (class 2) phases. Linear discriminant analysis (LDA) was then applied to these data in order to find the set of axes that maximally separated the 2 classes.

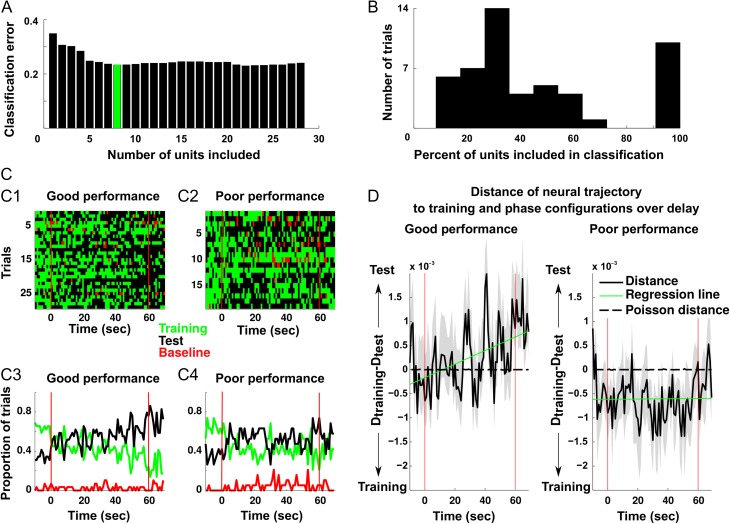
LDA when performed on data with multiple features (i.e., single units) can be prone to over-fitting when trained on a subset of data. The weighting of the potentially irrelevant features may slightly improve the classification of one subset of data while impairing the classification of other subsets (Kohavi and Kohavi 1997). In order to identify the subset of single units encoding the training/test phase distinction, while preventing over-fitting, we performed forward sequential feature selection using the “sequentialfs” function in MATLAB. Units were randomly selected and sequentially added to an LDA classifier, which was trained using a random subset of data. Its performance was evaluated using a different random subset (Kohavi and Kohavi 1997; Lapish et al. 2008). The addition of units was terminated when a classification error reached its first minimum (e.g., green bar in Fig. 6A). In order to obtain the random subsets, 10-fold cross-validation was performed via the “sequentialfs“, “crossval”, and “cvpartition” functions in MATLAB and implemented as follows. About 3877 time bins from training-phase and 3877 from test phase over 55 recording trials were used for classification. Each time bin contained the average activation of every recorded neuron over a 1-s time window. The spike counts for all neurons in these time bins were then submitted to LDA classification. The classifier was trained on 9 of the training/test phase time bin clusters and was then used to predict whether the remaining time bin was extracted from the training or test phase. This classification was performed 50 times to obtain an estimate of classification accuracy. The entire process was then repeated 300 times using randomly selected subgroupings of neurons. Each repetition yielded 300 predictions about task-phase membership for each time bin, based on the differences in ensemble spike count patterns for the training and test phases. The number of times the classifier made the correct predictions was counted and the subgrouping of neurons that achieved the highest prediction accuracy was identified (e.g., Fig. 6A, green bar). Final classification accuracy was reported after 50 more repetitions of 10-fold cross-validation on the identified subgroup. The trained classifier was then used to predict whether the spiking patterns for time bins extracted from the delay phase were more similar to patterns found in the training-phase versus the test phase.

Figure 6.

mPFC units that encode the distinction between training and test configuration gradually approach the test configuration during delay. (A) A representative example of a data set with 28 units where feature selection was used to identify a subset of units that optimally decode the training and test phases. In this example, the first 8 units minimized classification error (green). (B) The distribution of the number of units required to minimize classification error in all of the data sets. (C) The outcome of the classification for every second of the delay period is shown for good (C1) and poor (C2) performance trials and corresponding average classification across trials (C3, C4). Black squares and lines indicate that a neural activity pattern most resembling the test phase was identified in the 1 s window. Conversely, green squares/lines indicate a neural activity pattern most representative of the training-phase. Finally, red squares/lines represent classification as similar to firing before start of the trial. (D) To identify if a neural activity pattern at a given time during delay more closely resembled the training or test phase configuration, the Euclidean distance from each was quantified for 1 s windows in the delay. To determine which task-phase the neural activity pattern most closely resembled, the difference between each of the preceding values was computed. In good performance trials, the units transitioned from a training-phase configuration to the test phase configuration, but not on poor performance trials, thus indicating that remapping at the end of the delay was important for optimal task performance.

To further verify LDA classification results, the same data were analyzed using another independent means of classification. For this analysis, we used vectors of neural activity patterns from each data set independently in 1-s time windows (t) over the delay (v_t). To determine if mPFC activity during the delay more closely resembled a training or test phase configuration, we compared each vector in trials where more than 3 single units were recorded simultaneously (n = 28 trials) to the average neural activity patterns during the training and test phases. In order to do this, the Euclidean distance (d_t) from every vector (v_t) to the average training configuration $\stackrel{\circledR }{{\mathit{v}}_{\mathrm{training}}}$ was compared to the distance to the average test configuration $\stackrel{\circledR }{{\mathrm{v}}_{\mathit{test}}}$: ${\mathit{d}}_t=\Vert {\mathrm{v}}_t-\stackrel{\circledR }{{\mathrm{v}}_{\mathrm{training}}}\Vert -\Vert {\mathrm{v}}_t-\stackrel{\circledR }{{\mathrm{v}}_{\mathrm{test}}}\Vert$. The distance ${\mathrm{d}}_t$ indicated whether the delay vector at time t was more similar to the training or test phase activity patterns. This was used to characterize delay phase activity during poor versus good performance trials (Fig. 6D). Slopes of change throughout the delay were compared via ANCOVA for good and poor performance trials. For comparison, theoretical Poisson processes exhibiting the identical firing rate means and variances as the recorded neurons were generated 100 times for poor and good performance trials using standard fitting functions and again compared using an ANCOVA.

Results

Theta Activity Increased to Arm Choices and Reward Approach

Theta-band activity was prominent in HC and mPFC throughout the task (Figs 1C1, 2A1–2A2) and field potentials in both regions were highly coherent at the theta frequency (Fig. 1C2). Increases in HC theta power were observed throughout the task but were not precisely correlated with the time spent in a given location (Fig. 2C1). However, a temporally delayed relationship was observed related to the animal's movement velocity (Fig. 2C2). Bouts of theta tended to occur near the entrances to maze arms and during movement from the entrance to the reward cup (Fig. 2C3). Cross-correlation analysis of 10-s windows centered on reward revealed that changes in HC theta power throughout the entire task preceded peaks in movement velocity by approximately 0.21 s (Fig. 2C4, maximum value of average cross-correlation function). Peaks in HC theta power tended to precede arrival at the food cup by about 2 s (Fig. 2D1,D2; FDR-corrected 1-sample T-tests (H_o: μ = 0), P's < 0.05 at all times except when z-scored power approaches zero at ~ −0.75 s before reward).

Theta Power, Coherence and Phase-Locking Increased Throughout the Delay Period

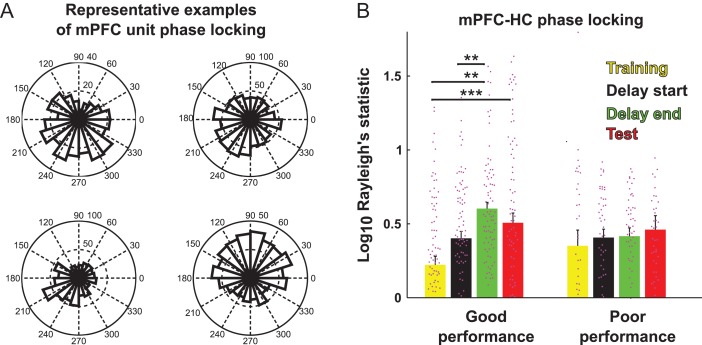
Theta power was highest during the second half of delay period and the test phase (Fig. 3D, main effect of task-phase, RMANOVA, HC: F_3,78 = 11.233, P = 3.33 × 10⁻⁶, mPFC: F_3,78 = 13.7, P = 2.84 × 10⁻⁷). Similarly, HC–mPFC coherence was also highest in the second half of the delay (Fig. 3D, main effect of task-phase, RMANOVA F_3,78 = 4.16, P = 0.00871). Furthermore, 20% of mPFC units (n = 180) were significantly phase-locked to the HC theta rhythm (Fig. 4A) and similar to theta power and HC–mPFC theta coherence, the phase-locking was also higher during the second half of delay than the first half or during the training-phase (Fig. 4B). Therefore, the largest changes in power and coherence during the task arose specifically during the delay period. This was the case even though the rats were locked in an arm during the delay and their movements were constrained.

Figure 4. m.

PFC units entrain to hippocampal theta in the second half of delay periods. (A) Example rose plots of mPFC units significantly entrained to hippocampal theta. Data from entire trials with good performance are included. (B) mPFC units significantly entrained to HC theta get progressively more entrained as trial progresses to the second half of delay. This occurred only on trials with good test performance (B, left) but not poor test performance (B, right, Tukey's multiple-comparisons test, *P < 0.01, **, ***, P < 0.001).

Delay-dependent changes were most prominent during trials where the animal's performance was good (Fig. 3F). The slopes of the of the regression line fit to theta power values recorded throughout the delay were more positive on trials with one or fewer test-phase errors (good performance trials) than on trials with 3 or more test phase errors (poor performance trials) (Fig. 3G, 2-way ANOVA, F_1,94 = 8.24, P = 0.0051). Likewise the increase in mPFC phase-locking to HC theta was only observed on good performance trials (Fig. 4B, RMANOVA, main effect of time, F_{3 ,417} = 6.45, P = 0.000281, performance × time interaction, F_{3 ,417} = 2.75, P = 0.0427). Therefore, if the animals were performing optimally, mPFC and HC theta became stronger and more robustly synchronized later in the delay period.

Distinct Network States are Observed in mPFC during Delay and Test Phases

Since the relationship between HC and mPFC activity became more robust during the second half of delay, we used PCA to explore whether the main firing rate patterns of mPFC neurons also evolved throughout the delay. PCA was performed on the matrix containing all neurons from all trials (n = 710 single units). The 2 top principal components (PCs) reflected distinct temporal patterns of neural firing that changed throughout the delay period. Specifically, the activity of neurons loading positively onto PC1 (Fig. 5A, black) were most prominent prior to delay onset and again after test onset. In contrast, those positively loading onto PC 2 (Fig. 5A, green) changed their firing rates progressively throughout the delay.

Since PCA was run once on the data from all neurons and trials, it was possible to compare how an individual PC varied from one trial to the next. Overall, neural activity associated with PC 2 activation was greater on good performance trials as compared with poor performance trials (Fig. 5B, RMANOVA, main effect of time, F_{5 9,13 865} = 3.16, P = 5 × 10⁻¹⁵, time × performance interaction, F_{5 9,13 865} = 1.34, P = 0.041). We then tested whether units most strongly contributing to this pattern also tended to be those that were phase-locked to HC theta. Indeed, those single units exhibiting the top one-third (33%) highest absolute loadings on PC 2 (n = 237 single units) had higher phase-locking values than neurons exhibiting the one-third lowest absolute loadings on PC 2 (33%, n = 237 single units) (Fig. 5C, RMANOVA, main effect of loading, F_{1 ,704} = 10.4, P = 0.0013). Thus, in trials where performance was good, a unique activity pattern emerged that was dominated by neurons whose spike rate and phase-locking to HC theta increased progressively throughout the delay.

Evolution of Task-Phase Encoding Throughout the Delay Period

The data presented above showed that firing and theta phase-locking tended to increase throughout the delay, but did not indicate whether the content of the information represented also changed dynamically throughout the delay. To address this issue, a LDA-based classification was implemented that classified the patterns of activity across neurons in each trial as being more similar to the activity expressed during the training (class 1), the test (class 2), or the baseline (class 3) phase of the task. A cross-validation procedure was used whereby the time bins used to train the classifier were different from those used to test it (see “Materials and Methods” section). Overall the classifiers were good at determining which class (i.e., task-phase) a given randomly chosen time bin belonged (Fig. 6A). In order to extract the neurons that most accurately encoded task-phase, a procedure known as sequential feature selection was used in which classifier performance was evaluated when neurons were substituted into and out of the ensemble. The results of sequential feature selection classification procedure yielded a specific subset of single units from each data set that optimally encoded task-phase with an accuracy above 70% (Fig. 6A,B). Across all data sets this resulted in 256 units that contributed to optimal classification. Of these 256 neurons, 59 were those identified above that also loaded strongly onto PC 2 and exhibited significant phase-locking in the latter half of the delay. Given that the chances of finding a neuron that loaded strongly onto PC 2 and that exhibited significant phase-locking was 0.140 (n = 35) in the general population, 59 neurons are no more than what would be expected by chance in a population of 256 (1-tailed binomial test, P = 0.311). In other words, neurons accurately encoding task-phase information were no more likely to exhibit an increase in firing and HC phase-locking throughout the delay than neurons in the general population.

The preceding analysis identified a set of 256 neurons that optimally encoded task-phase information when the bins to be classified were derived from the baseline, training or test phases of the task. Since a main goal of the present study was to determine how information was encoded during the delay phase of the task, we next used the trained classifiers to ask which of these 3 task periods did activity during the delay most resemble. The assumption was that firing patterns resembling those recorded during the training-phase would be indicative of retrospective code whereas firing patterns resembling those emerging in the test phase would be indicative of prospective code. To ensure that classification accuracy was not confounded by variations in behavior, trials were first divided based on the task performance. The results revealed that activity during the delay resembled both training-phase and test-phase activity patterns to varying degrees across trials, but rarely resembled baseline activity (Fig. 6C). The fact that activity rarely resembled baseline activity indicated that both training and task-phase patterns were truly unique and classifications were not being made randomly. Overall across trials, bins early in the delay period were essentially equally likely to be classified as belonging to class 1 (i.e., like the training-phase activity pattern) as class 2 (i.e., like the test-phase activity pattern). Yet later in the delay, it was more likely that bins would be classified as being more similar to the test-phase than training-phase pattern (Fig. 6C). A similar shift was not detectable on trials where performance was poor as both patterns were equally represented across the delay period. This suggested that in trials where the animals performed well, there was a shift from a mixed retrospective/prospective code to more of a pure prospective code throughout the delay.

To statistically quantify this result, a different procedure was used in which we calculated the Euclidean distance in the MSUA spaces between the 2 task-phase activity-state clusters on a trial by trial basis (see “Materials and Methods” section). When these distances were compared using an ANCOVA, time (F_{1 ,1736} = 4.46, P = 0.035) and time × performance interaction effects (F_{1 ,1736} = 4.68, P = 0.031) were observed. In good performance trials, significantly more bins were classified as resembling the training-phase pattern in the first (n = 348) than the second half of the delay (n = 300, χ²_(N=837,DF=1) = 5.80, P = 0.0016) whereas there were more bins classified as belonging to the test phase pattern in the second half of the delay (n = 490) than the first (n = 440, χ²_(N=837,DF=1) = 6.05, P = 0.014). Therefore, a transition from the encoding of training to encoding of test information appeared to be associated with successful task performance in this subgroup of neurons. Finally, we created a surrogate data set using a theoretical Poisson process that generated a spike count matrix exhibiting the identical means/variances to those of the recorded neurons during the training and test phases of the task. While the first and second moments of the spike count distributions were identical, the firing patterns across the neurons at each time bin were random. We then calculated the Euclidean distances between the theoretical “training” and “test phase” clusters in the MSUA space and compared them to the distances between the actual training-phase and test phase clusters (Fig. 6D, dotted lines). Note that the means of these randomly generated distances remained close to zero but were different from those of single units (FDR-corrected paired t-test, P < 0.05 in 96% of the time bins). On the other hand, mean distances of actual data during good performance trials (Fig. 6D left, solid line) increased steadily, indicating a gradual shift in the ensembles to the test phase configuration during the delay period (ANCOVA, time (F_{1 ,1736} = 4.46, P = 0.035) and time × performance interaction effects (F_{1, 1736} = 4.68, P = 0.031)).

Discussion

The current study is the first to explicitly examine mPFC-HC dynamics reflected retrospective versus prospective coding of information during a delay period of a working memory task. These data add to a number of previous studies that examined the firing properties of neurons in the mPFC of animals performing similar tasks (Jung et al. 1998; Pratt and Mizumori 2001; Lapish et al. 2008, 2015; Balaguer-Ballester et al. 2011). Results showed that a subpopulation of mPFC neurons increased their firing and became entrained to HC theta rhythms during the second half of the delay period. As the delay progressed, ensemble activity also began to resemble the activity-state patterns that would emerge during the forthcoming test phase. These changes were only observed in trials with good behavioral performance and, therefore, may represent a preparatory process in which previously acquired information is used to generate an optimal prospective foraging strategy.

Optimal foraging involves a mixture of both retrospective and prospective coding strategies that depend on task demands (Cook et al. 1985). A retrospective strategy is sufficient to perform a single phase working memory task without a delay, as the rat need only remember the arms it visited previously within the trial. Likewise, delayed working memory tasks that involve only 2 choice alternatives could also be effectively solved using primarily a retrospective strategy. However, using an exclusively retrospective strategy to solve the 8-arm DSWS task would be difficult as the rat would have hold in memory each of the arms it visited during the training-phase as well as the arms it visited during the test phase. To reduce memory load, it is more efficient to maintain a prospective memory of the 4 previously blocked arms that are to be visited during the forthcoming test phase. This could then be augmented by using retrospective memory to keep track of recent arm choices.

A long-standing view derived from the study of primate dorsolateral PFC neurons, is that delay-period activity represents the online maintenance of previously acquired information (Funahashi et al. 1989; Baeg et al. 2003). In support of this view, a recent study in rodents reported that inactivation of HC–mPFC projection impairs task performance when delivered prior to the sample but not choice phase of a delayed nonmatch to position task (Spellman et al. 2015). However, other studies have raised questions about the importance of mneumonic representations in rat medial frontal cortex neurons (Horst and Laubach 2012; Hyman et al. 2013) as well as whether working memory arguments derived from the study of the primate dorsolateral PFC should be applied to the rat mPFC since the areas are not strictly homologous (Passingham and Wise 2012). Our past studies have shown that transient lesions of either the prelimbic or anterior cingulate subregions of mPFC delivered at the end of a 30-min delay period on the DSWS task both disrupted test phase performance whereas the same lesions delivered immediately before or after the training-phase had no effect (Seamans et al. 1995). Transient asymmetric inactivations of the prelimbic cortex and HC at the end of the delay period also produced the same impairment (Floresco et al. 1997). Therefore, during performance of complex tasks that utilize prospective encoding of multiple items, information does appears to be transferred between the HC and prelimbic cortex at the end of the delay, just prior to the choice event. In the present study, when task performance was optimal we observed that theta power and synchrony between the HC and ACC were greatest at the end of the delay period (Figs 3 and 4). Collectively, these data imply that synchrony between the HC and both the prelimbic and ACC subregions of mPFC are critical for optimal performance when choices are made at the end of extended delay periods. Thus, the changes in neural activity and synchrony observed herein may reflect a preparatory process during the test phase as distinct from earlier encoding of information or the maintenance of a retrospective working memory trace. While this preparatory process could reflect the formation of a trace of the to-be-selected test phase arms it may also provide a much broader function. For example, an animal preparing to forage at the end of the delay would be required to use the rules of the task (e.g., win-shift) to guide the selection of arms in the test phase. In this way, the changes in neural activity patterns in mPFC at the end of the delay might provide a mechanism to translate goal-states (e.g., obtain food) into the action plans required to achieve them.

At a mechanistic level, increases in theta-band synchrony at the end of the delay could optimize the information transfer between the HC and mPFC (see Lisman and Idiart 1995). Specifically, the synchronous neural firing of HC and mPFC neurons along a theta cycle could promote spike time dependent plasticity and the formation of functional assemblies across the 2 brain regions (Miller 1991; Siapas et al. 2005; Benchenane et al. 2010). Given the importance of the HC in the memory for places, enhanced connectivity could transmit the locations of the previously baited training-phase arms to the mPFC. It is also possible that the HC provides more abstract information to the mPFC about future options. For example, multiple studies provided evidence of anticipatory activity in the HC (Ferbinteanu and Shapiro 2003; Itskov et al. 2008; Pfeiffer and Foster 2013; Catanese et al. 2014; Redish 2016). During this “vicarious trial and error” encoding, HC place cells fire in a manner consistent with “imagining” possible behavioral paths at decision points of a maze (Johnson et al. 2007). This is similar to the phenomenon observed here (Fig. 6) as the activity of mPFC ensembles began to progressively resemble the patterns that would emerge as the animal successfully foraged during the forthcoming test phase and would be precisely the type of coding necessary to form a prospective memory trace. Alternatively, or in addition, progressive increases in firing throughout a delay (Fig. 6) are thought to provide a “ramping”-based mechanism for interval timing (Durstewitz 1999; Reutimann et al. 2004; Narayanan 2016). If this timing mechanism were to integrate information from the HC about imagined paths, it would allow mPFC ensembles to determine the likely path and transit time to forthcoming rewards, which could be provide vital information for optimizing foraging decisions. In this sense, interactions between the HC and mPFC in the form of delay period synchrony and the emergence of test-phase activity-state patterns may reflect the neural basis of “working with memory” (Moscovitch and Winocur 1992) or the ability to take previously acquired information and use it to flexibly generate a prospective plan of action.

Funding

This work was supported by National Institute on Alcohol Abuse and Alcoholism (grants AA022821, AA023786, and P60-AA007611 to C.C.L.) and Canadian Institutes of Health Research (grants MOP-93784 and MOP-84319 to A.G.P.; MOP-93784 and MOP-84319 to J.K.S.).