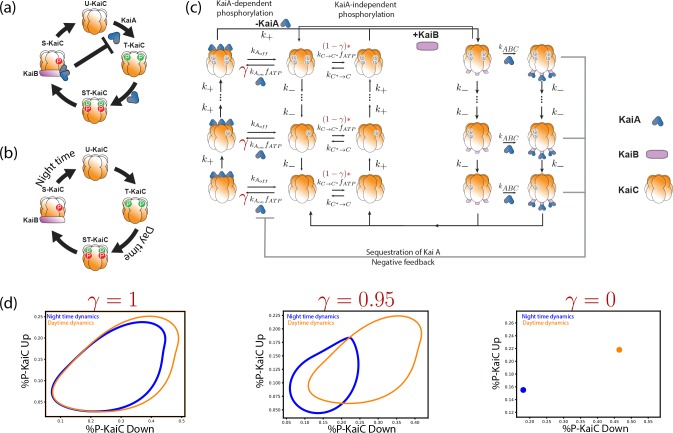
Appendix 1—figure 1. Explicit biochemical KaiABC model simulated using the Gillespie algorithm.

(a) The experimentally well-characterized clock in S. elongatus consists of a negative feedback-enabled self-sustained oscillator. KaiBC complexes sequester KaiA, preventing runaway KaiC molecules from going through the cycle independently. (b) The genome of P. marinus lacks kaiA. We assume a minimal model consistent with known facts (Rust et al., 2007) about this clock; KaiC phosphorylation proceeds without KaiA and hence different KaiC hexamers can proceed independently through the cycle. (c) We combine both clocks in one model with an interpolating parameter $\gamma$ that selects between an S. elongatus-like KaiA-dependent pathway and an P. marinus-like KaiA-independent pathway. All reactions shown are assumed to be first order mass-action kinetics. We simulate such a system at different overall copy numbers $N$ using the Gillespie algorithm. (d) We find limit cycles for $\gamma >0.9$. The resulting limit cycles for $\gamma =1,0.95$ violate the simplifying assumptions used in our dynamical systems (e.g., non-circular cycles of different size); and yet our results are qualitatively validated by this model (Figure 1d from the main text).