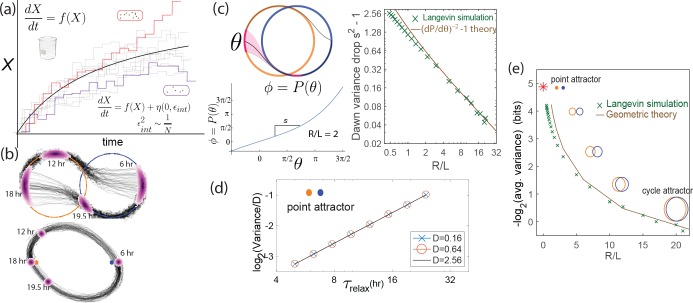
Figure 5. Internal fluctuations severely affect continuous attractors but not point attractors.

(a) We model fluctuations due to finite copy number $N$ as Langevin noise with mean zero and standard deviation ${ϵ}_{\text{int}}$, resulting in a diffusion constant ${ϵ}_{int}^2\sim 1/N$ for the clock state. (b) The flat direction of limit cycles cannot contain diffusion, leading to large increases ${ϵ}_{int}^2{T}_{day}$ in population variance of clock state during each day (and night). In contrast, point attractor dynamics have constant curvature at all times, leading to a constant population variance over time. (c) The variance drops ${\sigma }^2\to {\sigma }^2/s^2$ at dawn and dusk for limit cycles during the off-attractor dynamics between the day and night cycles. As with external noise, the variance drop is predicted by the slope $dP(\theta )/d\theta$ of the circle map between the cycles. This dawn/dusk drop goes to zero for large $R/L$ limit cycles but variance still increases during the day and night. (d) The variance for point attractors is $D{\tau }_{relax}$, a constant determined by the curvature ${\tau }_{relax}^{-1}$ of the harmonic potential. (e) Thus, with only internal noise present, the precision of limit cycle clocks increases with increasing separation $L/R$, asymptotically approaching the performance of point attractors.