Figure 1.

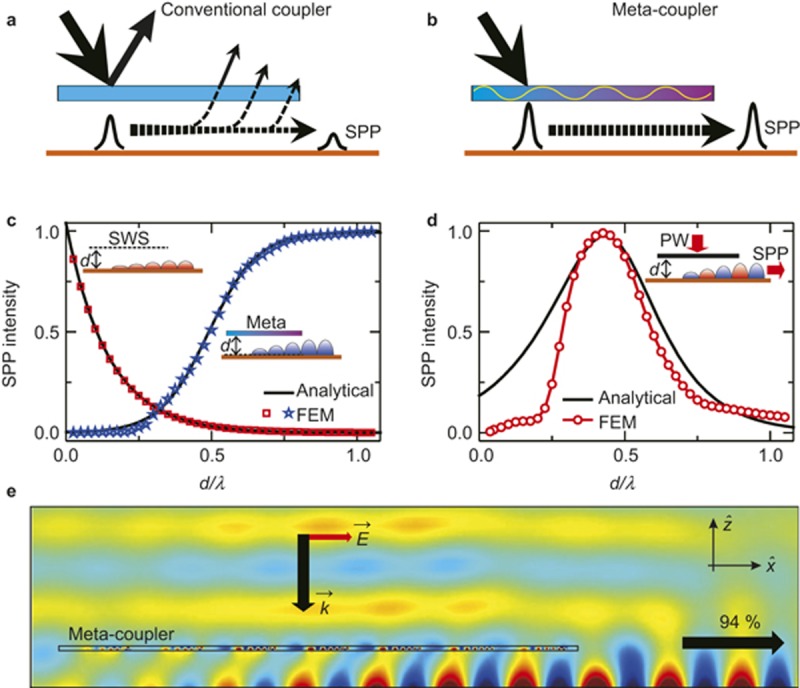
Device configuration, working principle, and coupling efficiency of the SPP meta-coupler. (a) Key factors that degrade the efficiencies of conventional SPP couplers (such as grating couplers and prism couplers): the initial reflection at the device surface and the decoupling from SPPs to free space. (b) Configuration of our SPP meta-coupler: a transparent gradient metasurface is placed at a distance d above the target plasmonic metal. The incident wave is first converted into a driven SW bound on the metasurface and is then resonantly coupled to the eigen SPP wave on the plasmonic metal. Neither reflection at the metasurface nor decoupling from the SPP to free space occurs. (c) FEM-stimulated intensities of SPP waves generated on the plasmonic metal versus the distance d in the excitation (red symbols) and scattering (blue symbols) processes compared with those calculated using the analytical formulas given in Equations (1) and (2) with k₁= 210 m^-1, α = 357.8, and k₂=368 m^-1 (lines). (d) Excited SPP intensities as a function of d when the meta-coupler is illuminated by an impinging wave with constant power, obtained via FEM simulations of the effective-medium model (symbols) and analytical calculations based on Equations (1) and (2) (line). (e) FEM-simulated (H_y) field distribution in the case of SPP excitation by our meta-coupler in an optimized configuration (with d_c = 14.3 mm), showing that the highest SPP coupling efficiency is 94%. The ε_M(x) and μ_M(x) profiles are modified at the device corners and supercell boundaries to smooth the sharp discontinuities. In (c–e), the plasmonic metal (with ε_r = −4.33) supports an eigen SPP with k_SPP = 1.14k₀ at a working frequency of 9.2 GHz.