Tomographic flow cytometry by digital holography

Abstract

High-throughput single-cell analysis is a challenging task. Label-free tomographic phase microscopy is an excellent candidate to perform this task. However, in-line tomography is very difficult to implement in practice because it requires a complex set-up for rotating the sample and examining the cell along several directions. We demonstrate that by exploiting the random rolling of cells while they are flowing along a microfluidic channel, it is possible to obtain in-line phase-contrast tomography, if smart strategies for wavefront analysis are adopted. In fact, surprisingly, a priori knowledge of the three-dimensional position and orientation of rotating cells is no longer needed because this information can be completely retrieved through digital holography wavefront numerical analysis. This approach makes continuous-flow cytotomography suitable for practical operation in real-world, single-cell analysis and with a substantial simplification of the optical system; that is, no mechanical scanning or multi-direction probing is required. A demonstration is given for two completely different classes of biosamples: red blood cells and diatom algae. An accurate characterization of both types of cells is reported, despite their very different nature and material content, thus showing that the proposed method can be extended by adopting two alternate strategies of wavefront analysis to many classes of cells.

Introduction

To date, one of the most powerful imaging tools for analyzing biological samples is tomography, which is able to furnish complete characterizations in three-dimensional (3D)¹. Various classes of tomographic concepts exist, such as X-ray computed tomography, optical coherence tomography^{2, 3} and tomographic phase microscopy (TPM)^{4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}. TPM is based on quantitative phase imaging techniques for the accurate 3D refractive index (RI) mapping of cells, as demonstrated by Feld’s group at MIT⁴, or even by white light sources applied to red blood cells (RBCs), as shown by Popescu’s group^{7, 8}. Park and coworkers demonstrated a reconstruction of a 3D RI distribution employing sparse angle illumination^{5, 9, 11}. Ozcan’s group proposed a lens-free holographic microscope, which enables the imaging of a very large volume (tens of mm²) and the possibility to perform an optical in-flow tomography by exploiting a pixel super-resolution technique^{12, 13, 14}. Recently, Psaltis’ group proved a smart learning method for building tomographic structures^{15, 16}. TPM set-ups require the sample to be observed along different directions with respect to the probing beam. Recording is often accomplished by adopting beam deflection^{5, 14, 17}; however, in this case, some problems arise because the angles are limited to 150°, thus affecting the accuracy of the tomographic reconstruction. Alternatively, direct mechanical rotation of the sample⁶ is problematic because mechanically manipulating the biological specimen introduces the risk of altering the sample. Tomographic arrangements occasionally use holographic optical tweezers¹⁸ to rotate the sample without mechanical contact^{19, 20, 21}; unfortunately, they do not allow high-throughput and in-line useful conditions for continuous in-flow tomography. In another case, Heng et al.²² adopted an optofluidic microscope, for which the flow was used to provide a scanning mechanism; however, the sample rotation was considered an undesired effect.

In summary, to date, all tomographic methods require a high-precision, opto-mechanical and/or optoelectronic device to acquire a set of many images by probing the sample along a large number of controlled directions. Moreover, to successfully apply the tomography algorithms, each recorded image must be tagged with the correct cell’s rotation angle with respect to the probing beam, thus requiring robust and effective control of the angular positions. Overcoming such difficulties represents the main critical issue in all tomographic approaches and, in practice, limits the implementation of tomography, especially at the microscopic scale, because the current approaches are very cumbersome and unsuitable for widespread use in the life sciences. Here we present a technological improvement by demonstrating an in-line TPM approach that simplifies the optical set-up, thus opening a route for a real-world tool in the life sciences for single-cell analysis in continuous flow. Essentially, we show for the first time that the wavefront transmitted by the cells intrinsically carries information beyond the optical path lengths (OPLs) to obtain quantitative phase-contrast maps (QPMs). In fact, we prove that a wavefront transmitted through the cell also contains information on the value of its angular position with respect to the direction of the probing laser beam. We explain below how the angles can be extracted numerically from the QPMs by intelligent numerical processing through two different strategies, thus allowing TPM that is suitable for all types of cells by using a single laser beam without mechanical or electro-optical scanning.

The two strategies for angle recovery are conceived on the basis of the inner structure of cells. In particular, the rolling angles of cells with a homogeneous RI distribution are calculated by exploiting the biolens effect²³. Alternatively, rolling angles of cells with inhomogeneous RI are obtained by observing the QPMs’ mirror symmetry around the axis of rotation.

The proposed innovative approach has been tested with two different classes of biological samples having relevant impact in our life, that is, RBCs^{24, 25} (with homogeneous RI) and diatoms algae (DAs)^{26, 27} (with inhomogeneous RI). Note that RBCs and DAs have completely different external shapes and inner structures, although they are all quite simple. Moreover, RBC and DA are made of diverse materials.

Although RBCs and DAs are very different from a biological perspective, they have some features in common. In fact, RBCs and DAs have a crucial role in the health of the human body and our planet, respectively. Moreover, these materials are characterized by their high abundance: RBCs account for nearly a quarter of the total number of cells in the human body, and diatoms are responsible for over 40% of the photosynthesis that occurs in the world’s oceans, and without them, the ocean would be unable to support the amount of life that it does. Furthermore, diatoms are useful tools for monitoring environmental conditions and are commonly used in studies of water quality, and the morphology and content of RBCs (that is, hemoglobin) are important biomarkers for many severe blood diseases²⁸.

An accurate study of the full 3D structure and the content of such diverse types of cells is of vital importance for human health (regarding RBCs) and for the earth’s ecosystem (regarding diatoms); as a result, a simple diagnostic tool that can operate in a high-throughput mode is highly desirable to, for example, find and identify rare cells in blood or contaminants in oceans.

Here we exploit the random self-rotation of the cells while they are flowing along microfluidic channels^{29, 30, 31}, thereby avoiding the direct rotation of the cells or the use of laser-beam angular scanning. Furthermore, we demonstrate that a priori knowledge of the rotation angle in 3D is no longer necessary because it can be accurately retrieved from the intelligent processing of the QPMs. The only requirement is to have one full angular revolution of the cells inside the field of view of the microscope while they are flowing. We named this proposed approach Rolling-TPM (R-TPM). Moreover, this approach allows fast single-cell analysis in high-throughput modality because no mechanical or electro-optical angular scanning of the laser beam is required.

Regarding RBCs^{32, 33}, we demonstrate their full characterization in terms of several metrics, such as 3D morphology, corpuscular hemoglobin (CH), volume (V) and RI. Moreover, we demonstrate both identification and sorting capabilities for anemia blood disease, in which some of the RBCs parameters differ slightly from healthy ones. Regarding DA, we instead show the capability to obtain the outer structure and the detailed 3D inner structure of auto-fluorescent chloroplasts via whole R-TPM imaging without the recurring use of fluorescent imaging.

Materials and methods

Blood preparation and isolation of erythrocytes

Human blood (~4.0 mL) was collected in a 7.2-mg K₂ EDTA vacutainer tube (BD, Plymouth, UK) from a healthy volunteer. Blood was centrifuged at room temperature at 2500 r.p.m. for 15 min to separate RBCs at the bottom of the sterile centrifugation tube from the plasma and buffy coat. After centrifugation, the plasma and buffy coat were discarded, and the RBC pellet (~1.5 mL) was washed with a saline solution of 0.90% w/v of sodium chloride (NaCl) in sterile water in a 1:1 ratio and re-centrifuged at room temperature at 2500 r.p.m. for 10 min. After the second centrifugation, the supernatant fraction was removed, and an aliquot of isolated RBCs (~100 μL) was diluted in 10 mL of the saline solution of 0.90% w/v of NaCl in sterile water with a final osmolarity of 308 mOs mL⁻¹ to maintain the osmotic pressure of the RBCs. For the experiments, a final volume of diluted RBCs (~100 μL) was used. Altered RBC shapes were obtained by changing the buffer osmolarity, and a buffer of 205 and 410 mOs mL⁻¹ was used to perform experiments under hypotonic and hypertonic conditions, respectively.

Diatoms preparation

The two strains of diatoms (T. rotula CCMP 3264 and S. marinoi CCMP 2092) were purchased from the National Center for Marine Algae and Microbiota (Bigelow Laboratory for Ocean Sciences, East Boothbay, ME, USA). Microalgae were cultured in 75 cm² flasks in sterile f/2 medium at 20.0±1.0 °C. The artificial light illumination (100 μmol photons m⁻² s⁻¹) was provided by daylight fluorescent tubes with a 14:10 h light:dark photoperiod. Then, 5-mL subsamples of each culture were collected with serological pipettes under the fume hood and transferred to 15-mL falcons. Highly concentrated cultures were diluted with filtered (0.22 μm) sterile seawater and maintained at room temperature until the analyses/measurements were performed.

Holographic recording and reconstructions

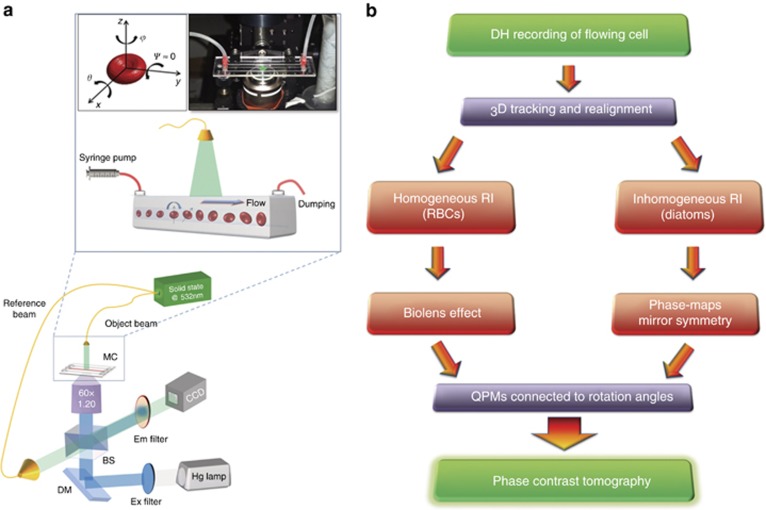
We built an optofluidic platform (depicted in Figure 1) to provide high-resolution images of both flowing and rotating samples. The DH modulus is made with a 400 mW fiber-coupled laser at 532 nm acting as the source for a Mach-Zehnder interferometer, whose main beam (in green) is directed into a customized inverted microscope equipped with a water-immersion 60 × objective, numerical aperture 1.20 microscope objective, thus allowing bright-field imaging of the cells. The reference beam (also in green) is recombined with the first beam by a beam splitter generating interference fringe patterns (the digital holograms) of the samples that are recorded by a 2048 × 2048 CCD camera (USB 3.0 u-eye, from IDS), recording at 75 fps in full frame. The optical lateral resolution is ~360 nm, and the axial resolution is ~170 nm³⁴. In our case, different from Cotte et al.³⁴, we are limited by the minimum detectable angle of rotation, that is, ~1° for this optical set-up.

Figure 1.

Working principles of the R-TPM approach. (a) Sketch of the experimental R-TPM set-up. Cells are injected into a microfluidic channel and tumble while flowing along the y-axis (inset of a). At the same time, a holographic image sequence is acquired. In the top-left corner of the inset, the reference system for cell tumbling is reported; in the top-right corner, a photo of the real set-up is shown. Rotation occurs around the x and z axes. BS, beam splitter; DM, dichroic mirror; MC, microchannel. (b) Flow chart representing the main steps of the two proposed algorithms for angle recovery and tomographic reconstruction.

The holographic recordings and reconstructions³³ occur as follows. First, through a digital holography apparatus, several out-of-focus digital holograms of cells (obtained while the cells are tumbling in the microfluidic channel) are acquired for different angular positions of the cell. Next, for each acquired hologram, the corresponding QPI is numerically calculated via the angular spectrum technique³⁵, which is a standard propagation algorithm that reconstructs the complex wavefield in terms of both amplitude and phase diffracted by the object at a certain distance from the hologram plane. The channel (by Microfluidic Chip Shop) is made of PMMA polymer and has dimensions of 1000 μm × 200 μm (width × height). At the bottom, the cover lid is 140 μm thick, which allows the use of the oil-immersion objective. The sample is injected into the channel by a syringe and capillary tubes furnished by the Microfluidic Chip Shop. For the experiments with diatoms, we added a fluorescence modulus (Figure 1a). Light from a fluorescence lamp (X-cite series 120 pc Lumen Dynamics) is directed onto the sample (blue path); a combination of excitation (GFP) and emission (Tritc) filters, which are suitable for detecting the diatom’s chlorophyll, is used, together with a dichroic mirror.

Fluid dynamic conditions for cells tumbling

After the preparation is completed, the cells are injected into a microfluidic channel by a syringe pump. In our experiment, the deformation of the RBCs is negligible. Theoretical studies and numerical simulations by G Gompper and coworkers describe the different ways that an RBC moves inside a microchannel, depending on the confinement and flow strength³⁶. In our experiment, with a very small confinement and flow strength, we observe the tumbling condition; that is, each RBC undergoes a rotation and can be approximated by a rigid body. By estimating the number of cells accomplishing a complete rotation (360°) in the field of view, we observe more than 150 rolling cells per minute. This throughput is several times larger than that obtained with classical TPM methods⁹.

Tomographic reconstruction

We use optical projection tomography³⁷, where the inputs of the filtered back-propagation algorithm are the aligned-oriented QPMs, and the rotation angles are around the x-axis, θ. The number of QPMs for each imaged cell in the field of view is ~200 for our camera with a frame rate of 75 fps. If the number of recordings decreases, then the resolution becomes worse, but the final shape reconstructions can be overlapped up to a lower recording limit of ~80 holograms. The calculation of the slices, which corresponds to the RI distribution of the sample along the planes orthogonal to the plane x–y, is performed through the inverse Radon transform. More specifically, for a given coordinate of the rotating axis in the plane x–y, the corresponding values of the QPMs along the orthogonal direction to the x-axis are collected for all rotation angles and are used together to calculate the corresponding slices by using the inverse Radon transform. Finally, these slices are joined together and processed to obtain a tomographic representation of the cell, that is, the 3D RI distribution. All numerical processing is performed off-line. By considering ~200 images, the angle recovery step requires a computational time of 11.2 s for RBCs and 16.8 s for DAs, and the projection tomography step requires 1.8 and 4.2 s for RBCs and DAs, respectively. Video-rate processing in tomographic phase microscopy has been recently demonstrated by using Nvidia’s CUDA C platform³⁸. An informal high-level description (that is, pseudo-code) of the operating principle of the whole tomographic reconstruction process, including the holographic 3D tracking step, rotating angle calculation using the two proposed methods and tomographic reconstruction algorithm, is reported in the Supplementary Information.

Results and discussion

The working conditions and the adopted optical system are depicted in Figure 1a. Cells tumble while flowing along a microfluidic chip probed by a single fixed laser beam. A second beam is used as a reference to generate interference fringes on the CCD camera. More details regarding the optical set-up are given in Materials and methods.

Hundreds of cells per minute have been analyzed; for each one, the hologram’s sequence is recorded, and the corresponding QPMs is retrieved. First, 3D holographic tracking is performed to re-align each cell with respect to its center of mass^{39, 40, 41}. Next, the rotation angles are numerically estimated using two strategies, the choice of which depends on the type of the cell under analysis. In Figure 1b, we report the conceptual block diagram summarizing the main steps of the two proposed strategies. In particular, the cells are classified according to their RI distribution (homogeneous and inhomogeneous). By this taxonomy, almost all classes of cells can be tagged, and the performance of the two proposed algorithms depends on their bio-physical features. To demonstrate the effectiveness of the two proposed strategies, we focus on RBCs as cells with homogeneous RI and DAs as cells with a more complex inner structure, that is, with inhomogeneous RI.

Specifically, RBCs can be modeled as optofluidic microlenses²³; thus, Zernike polynomials are used to quantify their aberrations. The flow direction occurs along the y-axis (see the reference coordinates system in Figure 1a), thus allowing the contribution of rotation angle ψ to be neglected. The other two orientations (θ and φ) are calculated by aberration analyses using Zernike fitting and are computed for each QPM. We reveal here that the trend of the focus shift term C₄ can be fitted by the square cosine function of the rotation angle θ and that the orientation φ can be retrieved from the tilt terms C₁ and C₂.

In Equation (1), r is the spatial coordinates vector, i(θ) denotes the ith QPM and corresponds to a specific rotating angle θ, Z_k is the Zernike basis functions and C_k is the corresponding Zernike coefficients. Each QPM is re-oriented to the first one of an angle equal to −φ.

For cells that have complex inner structures, such as DAs, we exploit an alternate intelligent image processing strategy. In fact, such cells have a detectable RI inner structure. It can be argued that a spatial symmetry exists in the reconstructed QPMs as a function of rotation angle. In particular, each QPM is compared with all others in the reconstruction sequence by searching for a twin-mirror QPM that maximizes their spatial correlation coefficient (SCC) because in these two directions, the OPLs should be equal for each pair of mirror pixels. Specifically, when the SCC of two QPMs is >0.95, if θ is in the range [0°, 90°], then we assign θ and 180°−θ as the rotating angles, whereas if θ is in the range [180°, 270°], then we assign θ and 540°−θ as the rotating angles.

In Equation (2), i and j with j>i are the ith and jth QPMs, respectively. Because not all QPMs may have a corresponding mirror QPM, we tag the remaining QPMs by assuming uniform angular rotation.

Finally, we use the optical projection tomography method to calculate the 3D RI distribution of the sample³², where the inputs of the filtered back-propagation algorithm are the aligned-oriented QPMs and the rotation angles around the x-axis, θ. Complete proofs of both mathematical relationships for retrieving the angles are reported in the Supplementary Information together with the holographic 3D tracking algorithm.

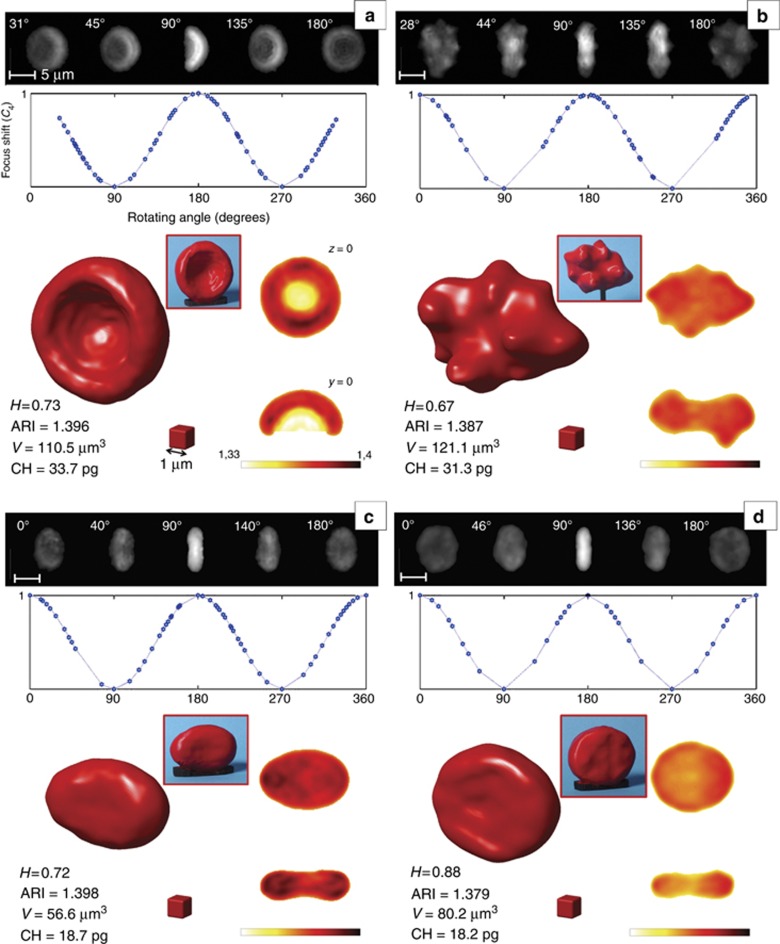
The results of R-TPM, as applied to RBCs, are reported in Figure 2 and Supplementary Movie 1. Four interesting cases are revealed. In particular, we examined both healthy (Figure 2a and 2b) and pathological (Figure 2c and 2d) RBCs, such as iron deficiency anemia and thalassemia, which are two highly diffused blood disorders. Specifically, some of the QPMs with the corresponding measured angles are illustrated on the top row of each panel of Figure 2. The inner plots show the rotating angle recovery approach, which was obtained from Equation (1). The final cytotomography results are displayed on the bottom side together with a picture of the correspondent central slices (z=0 and y=0 planes). In addition, the red boxes in the insets report a plastic model obtained by a 3D printer for educational purposes. In particular, we report the complete 3D RI distribution, and Supplementary Movie 1 display slice-by-slice the tomogram reconstructions and the inner RI map corresponding to the hemoglobin distribution. Figure 2a shows an abnormal RBC detected in the healthy sample, and a one-side concavity is present resembling the shape typically observed in hereditary stomatocytosis. Figure 2b shows one of the RBCs analyzed for the healthy sample in hypertonic solution, where the shape modification, as induced by the medium, provides the typical burr shape. We compare real cases with the simulated one (Supplementary Information) by means of the healthiness parameter, H, that is, the correlation coefficient between the measured and ideal 3D RI distributions. We assume that for 0.9⩽H⩽1, a RBC can be considered normal; otherwise, the deviation from the discocyte shape is not negligible. H values are reported for all of the cases presented in Figure 2 together with other global morphometric parameters, namely, the average RI, bio-volume (V) and CH (see Supplementary Information for details).

Figure 2.

R-TPM for RBCs. (a–d) Results of R-TPM, applied on RBCs presenting morphological anomalies (H<0.9) with respect to the ideal healthy one: (a) one-side concavity, (b) speculated, (c) iron deficiency anemic and (d) thalassemic RBC. For each RBC, we report the QPIs and the mathematical dependence of the defocus coefficient from the rotation angle and the tomogram retrieved by the QPIs and the RI distributions at the z=0 and y=0 planes. ARI, V and CH are also reported together with the plastic 3D representations realized by a 3D printer. The maximum measured standard deviation of the RI obtained by this technique is 0.003.

To verify the accuracy of the proposed approach, we have tested the R-QPM for two highly diffused blood disorders. The first sample, as shown in Figure 2c, is from a patient affected with iron refractory iron deficiency anemia (IRIDA) caused by mutations in the TMPRSS6 gene (L63Pfs13-W590R in compound heterozygosity)⁴². The second sample, in Figure 2d, is from a patient affected with alpha-thalassemia caused by a heterozygous deletional event of both in-cis HBA1 genes (—CAMPANIA in heterozygosity)⁴³. CBC reveals that MCVs are equal to 62.6 and 67.5 fl and that MCHs are 18.5 and 21 pg for the two patients, respectively. (Analysis performed by DAI.Med.Lab AOU Federico II University, Naples, Italy). In the case of anemia caused by an inherited defect in iron metabolism and thalassemia, the CH and V values are in good agreement with the analysis reported in the literature and, by comparison, with the CBC from patients with a similar genotype^{42, 43, 44}. Under our experimental conditions, the deformations of RBCs are negligible compared to the rotations they undergo, and the approximation of a rigid body is achieved^{36, 45} (see Materials and methods for details).

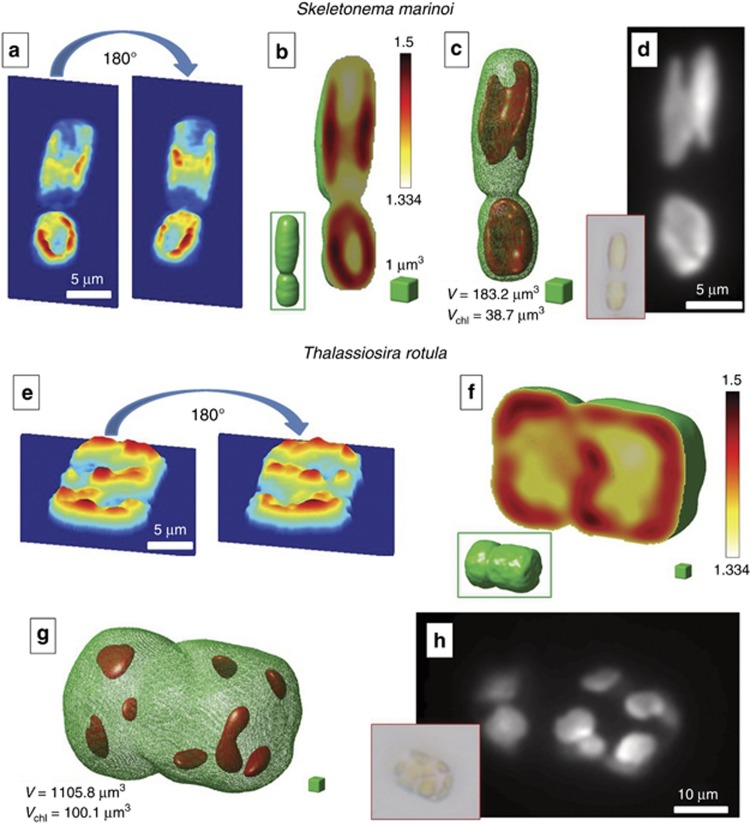
The second class of cells we investigated are DAs. These cells have a much more complex inner structure^{26, 27}. As a test case, we analyzed the Skeletonema marinoi and the Thalassiosira rotula diatoms, as shown in Figure 3 and Supplementary Movies 5 and 6. Figure 3a and 3e shows two mirror QPMs recovered by SCC maximization. The retrieved 3D RI distributions of diatoms are depicted in Figure 3b and 3f, where the external shape, labeled in green, is used to identify the whole occupied volume. The fascinating result for DAs is that by choosing the proper RI threshold, the tomographic algorithm reveals the real shape and dimensions of the chloroplasts and their location (Figure 3c and 3g), in perfect agreement with the corresponding fluorescence images (Figure 3d and 3h). In other words, the fluorescence acquisition or labeling of cells is, in principle, no longer necessary for R-TPM.

Figure 3.

R-TPM for DA. (a–d) Skeletonema marinoi and (e–h) Thalassiosira rotula. (a, e) Two mirror QPMs used to define the rotating angle retrieval rule. (b, f) Calculated tomograms, where the central slices are shown (the complete tomographic scan is provided in Supplementary Movies 5 and 6). Inset figures in the green boxes show the whole tomogram shapes, highlighting the volume occupied by diatoms given by the parameter V. (c, g) are obtained from (b, f), respectively, by applying a RI threshold to extract the 3D distribution of the chloroplasts and their volume (V_chl). (d, h) Fluorescence images used for comparison. Inset figures in the red boxes show the typical bright-field microscope images of the two diatoms.

The corresponding calculated volumes are V_tot=183.2 μm³ and V_chlor=38.7 μm³ for the Skeletonema, V_tot=1105.8 μm³ and V_chlor=100.1 μm³ for Thalassiosira. Note that the chloroplasts (which correspond to the fluorescence part of the cell) represent only a fraction of the entire volume. The tomographic reconstruction allows us to exactly identify their location and dimensions. This achievement is a key point as variations in chloroplast shape and location may be used in diagnostics at the genus level. Moreover, diatom chloroplasts are the main targets of some water contaminants, such as fluoranthene, which is one of the principal constituent of PAH-contaminated aquatic systems, and copper. It has been demonstrated that in the presence of these elements, chloroplasts show signs of structural rupture or even disintegration. Consequently, disturbances in the chloroplasts’ integrity could lead to an inhibition of photosynthesis, thus leading to a reduction in the amount of energy that is available to the cells. Due to structural damage, the function of the chloroplast may be affected; hence, algal cells will not be able to produce sufficient energy for growth and reproduction²⁷. As a result, the abundance of diatoms is commonly considered a valid indicator of ecosystem health.

Conclusions

In conclusion, the R-TPM approach is a single-cell analysis tool that allows the study of hundreds of cells and supplies as output their complete morphologic classification in 3D via the self-rotation of cells in microfluidic channels. Technological improvement obtained in the practical implementation of tomography is challenging because the wavefront analysis of the sample along different directions intrinsically carries not only QPM information on the OPL of the cell but also information about the rotation angles. An intelligent numerical process can easily extract the data of angles, thus allowing accurate phase-contrast cyto-tomography. This avoids cumbersome calibration and the use of any mechanical and/or optoelectronic device to control the rotation, thereby enormously simplifying the experimental system compared with the current state of the art^{4, 5, 8, 21}. By exploiting this concept, we have shown that it is possible to furnish a full 3D RI distribution for many types of cells flowing along a microchannel with a relatively simple internal RI distribution. Similar algorithms are under study to adapt the technique to more general cases, such as inhomogeneous RI cells with little symmetry.

The technique has been proved for cells with different shapes and characteristics, such as RBCs and DA. The R-TPM is simple, quick and reliable. A route for full screening at the single-cell level can be a quite challenging achievement by means of the proposed approach. Applications are foreseen, for example, in the isolation and characterization of ‘foreign’ cells in the blood stream and in revealing specific oceanic contaminants that threaten the ecosystem via the analysis of damaged chloroplasts.