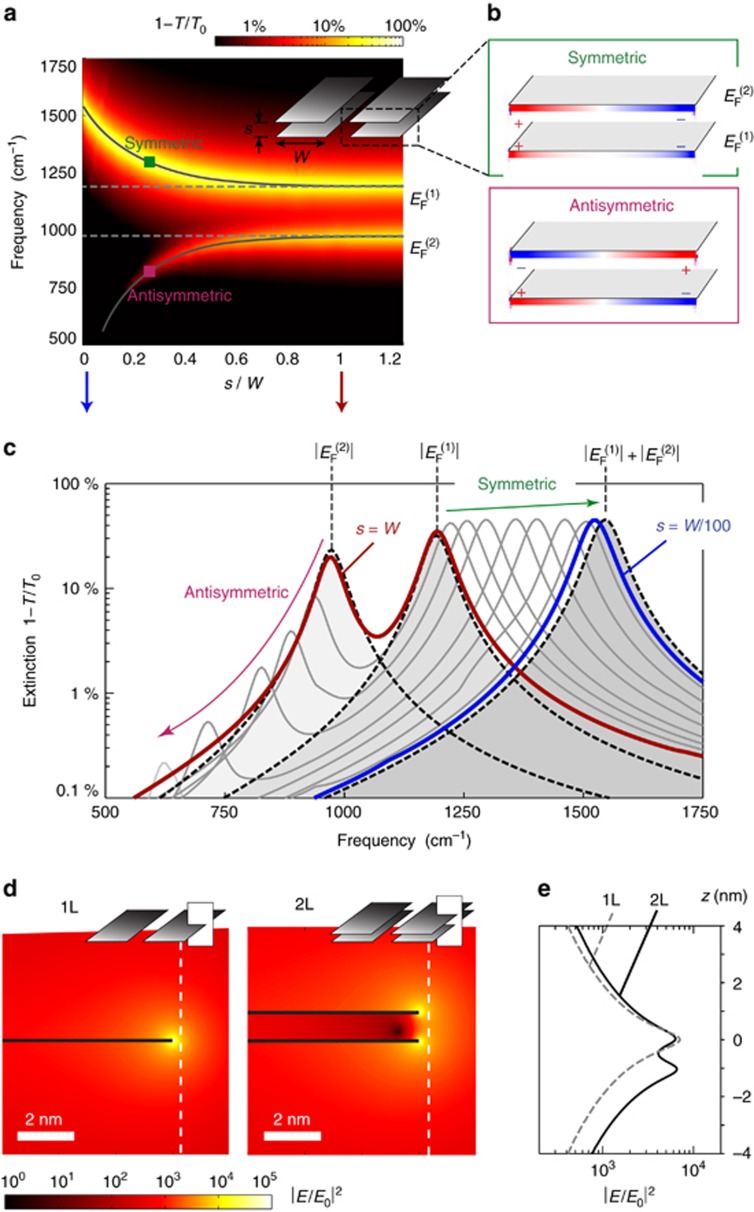
Figure 3.

Physical mechanisms and hybridization in 2L-GNRAs. (a) Simulated extinction coefficient of a 2L-GNRA for a variable interlayer separation s. The two graphene layers have Fermi levels |E_F⁽¹⁾|=0.3 eV and |E_F⁽²⁾|=0.2 eV, relaxation time τ=100 fs, the width of ribbons is W=40 nm and are embedded in a dielectric with refractive index n=1.4. Solid curves represent the resonance frequencies of the 2L-GNRA and dashed curves stand for the resonance of each individual layer, which correspond to the resonance of a 1L-GNRA with Fermi level |E_F⁽¹⁾| or |E_F⁽²⁾|. (b) Electric charge distribution across the ribbons for the 2L-GNRA with s=W/4 at the two resonance frequencies indicated in the figure. The high- (low-) resonance corresponds to a symmetric (antisymmetric) mode. (c) Simulated extinction spectra of the 2L-GNRA (solid curves) for an interlayer separation varying from s=W (red curve) to s=W/100 (blue curve). Dashed curves represent the extinction spectra of 1L-GNRAs with Fermi levels |E_F⁽¹⁾|, |E_F⁽²⁾| and |E_F⁽¹⁾|+|E_F⁽²⁾|. (d) Field enhancement distribution at resonance frequency for 1L-GNRA (|E_F|=0.3 eV) and for the symmetric mode of a 2L-GNRA (|E_F⁽¹⁾|=0.3 eV, |E_F⁽²⁾|=0.2 eV) with a separation s=1 nm. The field is presented for the cross-section indicated in the inset. (e) Field enhancement for the 1L- and 2L-GNRAs along the white dashed line in subfigure d.