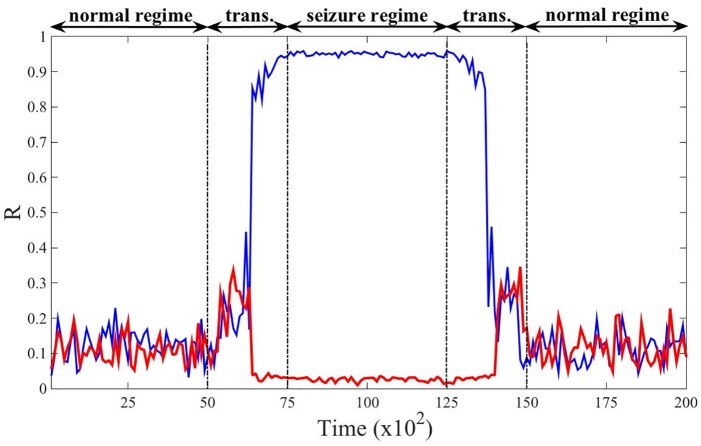
Fig 5. Onset of an epileptic seizure in the Kuramoto-like neuron population and the outcome of the controlled system.

We represent the order parameter R (blue curve for the KM model and red curve for the controlled version) as a function of time for N = 100 coupled oscillators linked using a Newman-Watts small-world network [55] with parameter p = 0.85 and M = 20 microelectrodes for the controlled case (γ/4 = 4.25). To smooth the results, each curve is the average over 20 independent realisations. We assume K to be small in the interval [0, 5000] fluctuating around the average value 0.1, during this period of time both systems behave similarly and do not exhibit synchronisation. Then we assume the coupling parameter starts to increase, t ∈ [5000, 7500], to eventually remain quite large, 0.5 on average, for t ∈ [7500, 125000]; we can observe that the KM falls in a synchronised state while the controlled one still does not exhibit synchronisation. Once the coupling parameter decreases and fluctuates again around a small value, 0.1, both systems recover the same non-synchronised state.