Fig. 2. Magnetic feSMs.

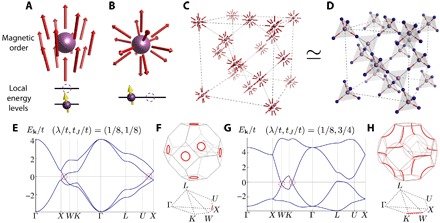
(A and B) Symmetries of a magnetic order can prohibit AIs at odd-site fillings. (A) The magnetic point group symmetries of a ferromagnetic arrangement are compatible with nondegenerate local energy levels. (B) However, those of the depicted hedgehog defect force all the energy levels to exhibit even degeneracies, which forbids AIs when a lone electron is localized to the purple site. (C) When hedgehog and antihedgehog defects are arranged into a diamond lattice, the previous argument suggests that no AI is allowed whenever the site fillings at the defect cores are odd. (D) The hypothetical magnetic structure in (C) could be realizable in spinel structures if the diamond sites are occupied by atoms with odd atomic numbers (purple) and the magnetic atoms (blue) at the pyrochlore sites exhibit an all-in-all-out magnetic order. (E to H) feSMs arising from the magnetically ordered Fu-Kane-Mele model (Eq. 6). (E) When the magnetically modulated hopping t_J is weak compared to the spin-orbit coupling λ, the fermiology is governed by rings of gap closing (circled in red), growing out from the original Dirac points at X when t_J = 0. (F) The positions of the rings in the Brillouin zone are shown in red. (G and H) For ${\mathit{t}}_{\mathit{J}}\ge 2\sqrt{2}\mathrm{\lambda }$, the nodal rings become connected at the momentum W. Thin lines indicate copies of the gapless momenta in the repeated zone scheme, included to illustrate the connectivity of the rings.