Figure 1.

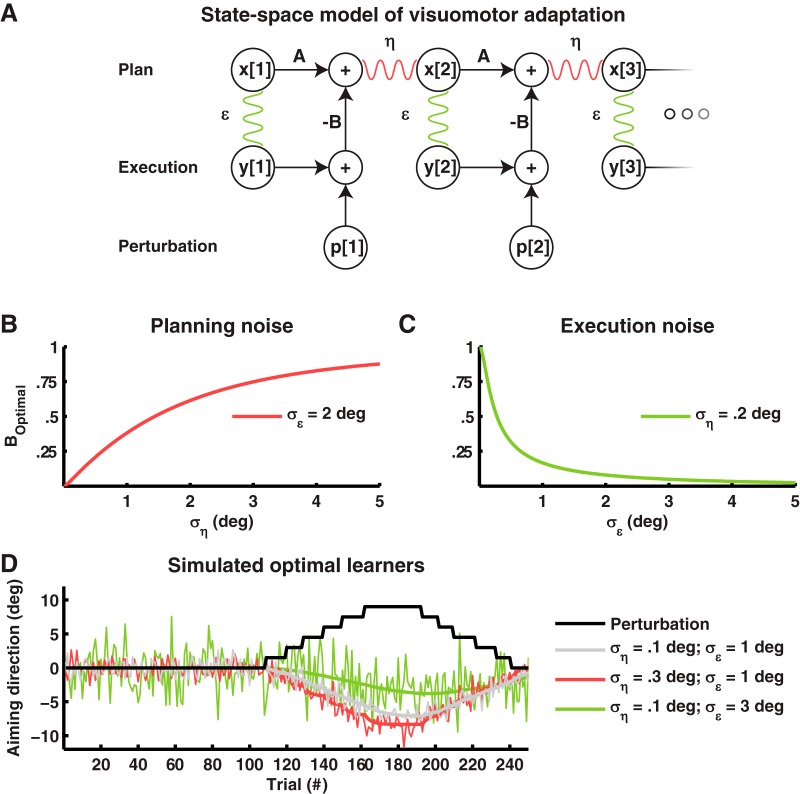
Planning and execution noise have opposing effects on visuomotor adaptation. A, State-space model of visuomotor adaptation. The aiming angle on trial 2 $x\left[2\right]$ is a linear combination of the aiming angle on the previous trial $x\left[1\right]$ multiplied by a retentive factor $A$ minus the error $e\left[1\right]$ on the previous trial multiplied with adaptation rate $B$. In addition, the aiming angle is distorted by the random process $\eta$ (planning noise). The actual movement angle $y\left[2\right]$ is the aiming angle $x\left[2\right]$ distorted by the random process $ϵ$ (execution noise). The error $e\left[1\right]$ is the sum of the movement direction $y\left[1\right]$ and the external perturbation $p\left[1\right]$. B, Planning noise and optimal adaptation rate $B_{Optimal}$ (defined as the Kalman gain). The optimal adaptation rate increases with planning noise ${\sigma }_{\eta }$. In this figure, ${\sigma }_{ϵ}$ was kept constant at $2°$. C, Execution noise and optimal adaptation rate $B_{Optimal}$ (defined as the Kalman gain). The optimal adaptation rate decreases with execution noise ${\sigma }_{ϵ}$. In this figure, ${\sigma }_{\eta }$ was kept constant at $0.2°$. D, Simulated optimal learners. At trial 110, a perturbation (black line) is introduced that requires the optimal learners to adapt their movement. The gray learner has low planning noise ${\sigma }_{\eta }=0.1°$ and execution noise ${\sigma }_{ϵ}=1°$. The red learner has a higher planning noise ${\sigma }_{\eta }=0.3°$ than the gray learner ${\sigma }_{\eta }=0.1°$. This causes the red learner to adapt faster. The green learner has a higher execution noise than the gray learner ${\sigma }_{ϵ}=3°$. This causes the green learner to adapt more slowly. For all learners, the thick line shows the average, and the thin line, a single noisy realization.