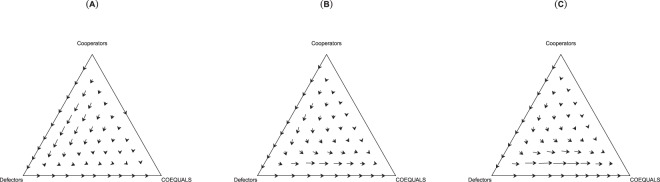
Figure 1.

Evolutionary dynamics of COEQUALS, defectors, and cooperators. Figure 1 presents phase diagrams reporting evolutionary dynamics in the baseline model when b = 2 [Panel (A)], b = 3 [Panel (B)], and b = 4 [Panel (C)], and all other parameters—save for population size—are set to their median values. In Panels (A–C), simplex vertices represent states in which all agents in the population adopt the adjacently listed strategy. Points along a simplex’s edges signify states in which agents adopt some combination of two strategies, whereas points within the simplex represent states in which agents adopt some combination of three strategies. Arrows indicate the population’s trajectory and the length of an arrow’s tail indicates the speed of population change, with longer tails signifying faster population change. Panel (A) indicates that the population gravitates toward COEQUALS more rapidly when a substantial portion of the population consists of defectors. For instance, when b = 2, P^D_g = 0.1, and P^C_g = 0.8, the proportion of the population adopting COEQUALS grows by only 1% over a generation. However, when b = 2, P^D_g = 0.8, and P^C_g = 0.1, the proportion of the population adopting COEQUALS grows by roughly 15% over a generation. Indeed, even when b = 2, COEQUALS grows to fixation from a state of universal defection (P^D_g = 1, P^C_g = 0). As Panel (B and C) indicate, when the gains to cooperation increase, agents adopt COEQUALS at a faster rate and a smaller proportion of defectors in the population are needed for a rapid advance toward universal adoption. In comparison with the above analysis, Panel (B) indicates that when b = 3, the proportion of COEQUALS adopters grows by 15% over a generation when P^D_g = 0.50 and the proportion of COEQUALS adopters grows by 33% when P^D_g = 0.80 and P^C_g = 0.1. When b = 4 [Panel (C)], the percent growth of COEQUALS adopters reaches 15% when P^D_g = 0.39. At P^D_g = 0.80 and P^C_g = 0.10, COEQUALS grows by 53% over the course of a generation.