Significance
Spontaneously formed nanoblisters are almost inevitable when transferring 2D crystals to a substrate. We hypothesize that those nanoblisters are filled with liquid according to our time-lapse atomic force microscopy scans and reasonable estimation of adhesion energy. We show that the liquid-filled nanoblisters form as a result of competition between the elastic energy of the deformed 2D crystal, the interfacial energy associated with van der Waals interactions, and surface tension of the liquid contents. Besides pointing to solutions for controlling their shape and internal pressure, our analysis provides a method to estimate the work of adhesion of 2D material interfaces by simply measuring the aspect ratios of the blisters, which is essential for the design and fabrication of 2D crystal-based applications.
Keywords: 2D materials, heterostructures, nanoblisters, adhesion, membrane theory
Abstract
Layered systems of 2D crystals and heterostructures are widely explored for new physics and devices. In many cases, monolayer or few-layer 2D crystals are transferred to a target substrate including other 2D crystals, and nanometer-scale blisters form spontaneously between the 2D crystal and its substrate. Such nanoblisters are often recognized as an indicator of good adhesion, but there is no consensus on the contents inside the blisters. While gas-filled blisters have been modeled and measured by bulge tests, applying such models to spontaneously formed nanoblisters yielded unrealistically low adhesion energy values between the 2D crystal and its substrate. Typically, gas-filled blisters are fully deflated within hours or days. In contrast, we found that the height of the spontaneously formed nanoblisters dropped only by 20–30% after 3 mo, indicating that probably liquid instead of gas is trapped in them. We therefore developed a simple scaling law and a rigorous theoretical model for liquid-filled nanoblisters, which predicts that the interfacial work of adhesion is related to the fourth power of the aspect ratio of the nanoblister and depends on the surface tension of the liquid. Our model was verified by molecular dynamics simulations, and the adhesion energy values obtained for the measured nanoblisters are in good agreement with those reported in the literature. This model can be applied to estimate the pressure inside the nanoblisters and the work of adhesion for a variety of 2D interfaces, which provides important implications for the fabrication and deformability of 2D heterostructures and devices.
Two-dimensional (2D) crystals are atomically thin, layered materials with strong bonding in the crystal plane and weak bonding via van der Waals (vdW) interactions between the layers (1, 2). Discovery of 2D crystals has fueled extensive fundamental and applied research due to their remarkable electronic, mechanical, optical, and magnetic properties. Rapidly emerging experimental and modeling results indicate that mechanical strains can strongly perturb the band structure of 2D crystals (3–5). In the nanoscale regime, the vdW interactions between the monolayer 2D crystal and its substrate can have strong influences on the mechanical behavior of 2D materials (6–8). Consequently, the performance of 2D-crystal–based devices relies heavily on the vdW interfaces. In reality, however, the vdW attraction between the 2D crystal and its substrate may cause adsorbed ambient molecules to lump together in the interface, resulting in micro- or nanoblisters which often degrade device performance (9, 10). Interfacial blisters are also frequently seen in vdW heterostructures (i.e., stacks of 2D crystals), causing significant charge inhomogeneity and limiting the carrier mobilities of a device (1, 2). Alternatively, due to the strong electromechanical coupling, nanoblisters have been applied for strain engineering of 2D materials (5, 11). Moreover, interface-confined chemistry was explored within 2D material blisters leveraging their high internal pressure (12–19). To either control or avoid blisters for the 2D materials, it is imperative to understand the formation mechanism for these nanoblisters and reveal the key parameters.
Many studies have been carried out recently to explore various aspects of nanoblisters, including the effects of heat (10), blister content (12), humidity dependence (20), and their shape characteristics (13). Although there is no consensus on whether the blisters are filled with air, liquid, or solid (21, 22), adhesion is one of the well-accepted governing parameters for the formation of blisters. In fact, interfacial blisters have been used as indicators of good adhesion between the constituents of vdW heterostructures (1), since blisters are energetically favorable only when the adhesion between layers is relatively high. Mechanics models have been developed and widely used to relate gas-filled blister profiles to interfacial adhesion (12, 20, 23–25). However, the subtle nature of the content inside the blisters may render the assumption of a gas content inappropriate. Direct application of this ad hoc model has led to unrealistically small adhesion values for graphene interfaces compared with well-established adhesion measurements (20).
In this work, we tracked the height of graphene blisters on SiO2 over the course of 3 mo. Extremely slow deflation of the blisters was observed, indicating that they are likely filled with liquid instead of gas content. We therefore developed a scaling law and a more rigorous analytical model based on the elastic membrane theory for liquid-filled nanoblisters. Compared with gas-filled blisters assuming ideal gas law for the content, the liquid blister theory assumes that the liquid inside the blister is nearly incompressible. However, the shape characteristics of the blister may vary depending on how the liquid interacts with the membrane and the substrate. Our analytical model is then compared with molecular dynamics (MD) simulations to provide a verification from the atomistic level. Like the gas blister theory, our liquid blister theory can also be utilized to quantitatively characterize the adhesion properties for the 2D materials based on the measured blister profiles. Alternatively, the blister shape, strain, and pressure characteristics can be controlled by tuning adhesion properties and trapped contents, which provides a viable guideline for the design of 2D material blisters for various applications.
Results
Shape Characteristics of Blisters.
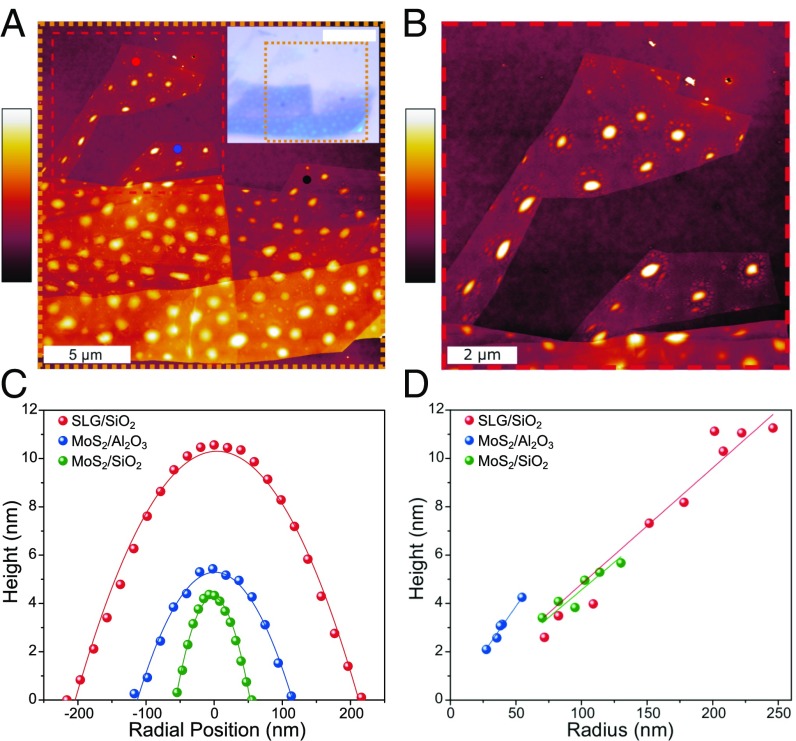
In this work, our experiments focus on the characteristics of nanoblisters that form at the graphene–SiO2 and 2D MoS2–SiO2 interfaces, as graphene and MoS2 are two of the most prevalent 2D materials so far. Additionally, we find blisters that form when chemical-vapor–deposited MoS2 is transferred to Al2O3. After mechanically exfoliating highly ordered pyrolytic graphite (HOPG) onto silicon wafer with native SiO2 (26), we identified single-layer graphene (SLG) areas that show a remarkably large number of blisters (Fig. 1A). The same procedure was also used to exfoliate 2D MoS2 flakes from its bulk crystal onto SiO2 (SI Appendix, Fig. S1B). For both samples, monolayer regions were identified using Raman spectroscopy (SI Appendix, Fig. S1) (27). Blisters trapped by SLG and few-layer graphene (FLG) in the optical micrograph appear as light-blue, circular regions, and are scattered throughout the flake (Fig. 1A, Inset). Using tapping-mode atomic force microscopy (AFM) (Fig. 1B), we can obtain the height profiles of the blisters. We denote the center height of the blister by h and its radius by a, such that the aspect ratio is given as h/a. The height and radius of the blisters are calculated by curve-fitting the assumed deflection profile for a pressurized membrane,
| [1] |
to the measured data (Fig. 1C). Further information on the experimental procedure for creating and characterizing blisters is provided in SI Appendix, section 1. To use the aspect ratio of a blister as a characterization method, the in-plane shape of the blister should be approximately circular such that the aspect ratio is reasonably consistent (see SI Appendix, section 1 for more information on the characterization of the nanoblister ellipticity). The shape of the blister may become distorted due to its local environment, causing the aspect ratio to become anisotropic. For example, in Fig. 1B blisters near the edges of graphene are elongated in the direction parallel to the edge leading to an elliptical instead of circular shape. Blisters with an elliptical shape can also be found along step edges in the FLG areas.
Fig. 1.
Interfacial blisters between 2D crystals and their supporting substrates. (A) Tapping-mode AFM reveals the complex distribution of HOPG-SiO2 blisters. (Inset) Bright-field optical micrograph where the orange dashed region corresponds with the large AFM image. (White scale bar: 10 μm.) The red, blue, and black dots indicate where Raman measurements were taken for SI Appendix, Fig. S2A. The color bar represents 0–17 nm. (B) A closer look at two monolayer regions from the red dashed region of Fig. 1A. Blisters close to the edges of the graphene are distorted from the typical circular shape. The color bar represents 0–13 nm. (C) By extracting the height profile of each blister, the height and radius is calculated by curve fitting a parabolic function. (D) Blisters for a specific interface show a consistent aspect ratio that is independent of volume.
Focusing on approximately circular blisters, the measured height vs. radius in Fig. 1D suggests that the aspect ratios of each type of the blisters are independent of the volume of the blister, with an average aspect ratio (h/a) of 0.049 ± 0.003 for the graphene–SiO2 blisters, 0.046 ± 0.004 for the MoS2–SiO2 blisters, and 0.083 ± 0.016 for the MoS2–Al2O3 blisters. A constant aspect ratio for a given 2D crystal–substrate pair has also been observed for other blisters reported in the literature (13, 20), indicating that the blister aspect ratio is a key dimensionless parameter for the material system.
Evidence of Confined Liquid.
The mechanical behavior of the blister is not only dictated by the 2D crystal–substrate interaction, but also by the interactions between the trapped content and the 2D crystal/substrate. However, so far there is no consensus or direct measurement of the blister content. While several previous studies applied the gas models to analyze those blisters (12, 20, 23, 28, 29), Geim and coworkers (13, 21) strongly advocated that the blisters are filled with hydrocarbons and liquid water. Emerging observations in literature imply that the blister content is likely to be water because those blisters are found to be highly dependent on temperature (especially beyond 100 °C) and humidity (10, 20). For example, Cao et al. (22) noted that the number density and size of blisters at the graphene–HOPG interface were reduced when exfoliation was carried out in a low-humidity environment compared with exfoliation in ambient conditions. In another case, Pizzocchero et al. (10) demonstrated that blister-free interfaces for heterostructures are possible only when the 2D crystal is transferred at 110 °C, and suggested adsorbed water is the most likely candidate for the contents of the interfacial blisters.
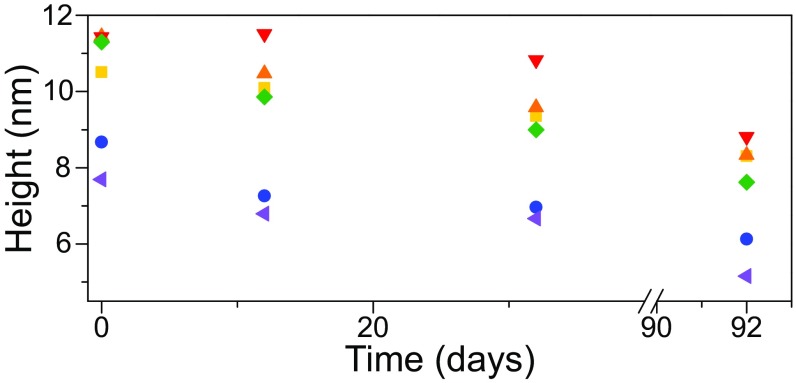
Here we monitor the time-dependent behavior of a selected number of blisters from Fig. 1A. As noted in previous studies, graphene–SiO2 interfacial blisters pressurized with gas typically deflate within 10 h for H2-filled blisters, and 7 d for N2-filled blisters (30–32). Since graphene is impermeable to even the smallest gas molecules (33), it was concluded that the majority of the gas content inside the blister escaped through the graphene–SiO2 interface. Over a period of 92 d, we performed AFM scans over the same sample using consistent scanning parameters and cantilever tips. Our data show that the blisters in the SLG regions exhibit deflation at different rates, with some showing little overall change in their height (Fig. 2), which is drastically different from the time-dependent behaviors of gas blisters. Hence our experiment offers evidence against the possibility of gas inside the blisters. We therefore suggest that the content inside the blisters is mostly liquid water, likely mixed with a certain amount of hydrocarbon contaminants. Following such hypothesis, in the following we present a liquid-filled blister model and adopt water as the most likely representative liquid for quantitative analysis.
Fig. 2.
Height measurements of SLG nanoblisters measured over a period of 92 d. All blisters show signs of gradual deflation, which indicates that the contents of the blister can escape through the SLG–SiO2 interface, but at a much slower rate than trapped gas molecules.
Modeling.
Although 2D crystals are atomically thin membranes, continuum mechanics has proven to be applicable when bending is negligible (34–36). We therefore employ an elastic membrane model to establish a direct relation between the aspect ratio of the blister and the material properties of the 2D membrane and substrate. Unlike gas-filled blisters considered in previous works (23, 29), where the ideal gas law was used to relate the pressure to the blister volume, we assume that the liquid inside the blister is nearly incompressible, but the aspect ratio () may vary depending on how the liquid interacts with the membrane and the substrate. We begin by using a simple scaling approach for determining the properties of axisymmetric blisters. The membrane over a liquid-filled blister of radius and height at its center is subject to a stretching strain from elementary geometry. With an in-plane elastic stiffness , the stretching energy in the membrane scales as . The bending energy of the membrane is negligible due to the thinness of the 2D membrane and relatively small aspect ratios. The adhesion energy required to form the blister is simply the energy change per unit area, , multiplied by the blister area, which scales as . If the volume of liquid () remains a constant in the blister, the elastic energy decreases and the interfacial energy increases with increasing . The competition leads to an equilibrium blister radius that minimizes the total free energy (), with . The scaling relation for the aspect ratio () is identical to that for gas-filled blisters (23, 29). However, the change of interfacial energy is different. For a gas-filled blister, is simply taken as the adhesion energy between the membrane and the substrate (). For a liquid-filled blister, considering the interfaces between the liquid, the membrane, and the substrate, the change of the interfacial energy can be written as
| [2] |
where , , and are the energy densities (per unit area) for the membrane–liquid interface, substrate–liquid interface, and the membrane–substrate interface, respectively. For blisters filled with liquid water, the Young–Dupré equations (37, 38) further lead to
| [3] |
In Eq. 3, is the work of adhesion (or adhesion energy) of the membrane–substrate interface, is the surface tension of water (∼0.072 J/m2) (38, 39), and and are the water contact angles of the substrate and the membrane, respectively. Thus, the scaling analysis predicts the aspect ratio for a liquid-filled blister as
| [4] |
where the dimensionless coefficient has to be determined by a detailed analysis (SI Appendix, section 2).
Clearly, by Eq. 4, the aspect ratio of a water-filled blister depends on the elastic property of the membrane, the adhesion of the membrane to the substrate, and the hydrophobicity of the membrane and the substrate. In addition, it should also depend on the shear interactions between the membrane and the substrate in the bonded region surrounding the blister. In previous studies of graphene blisters (8, 23, 25, 29), the edge of the blister is often assumed to be fully clamped onto the substrate due to adhesion and strong shear interactions that prevent sliding along the interface. However, a recent study (31) found that the shear interactions can be fairly weak between graphene and its substrate so that sliding may occur at the edge of the blister. As a result, the elastic deformation of the membrane depends on the shear interactions with the substrate, which means the coefficient in Eq. 4 depends on the shear interactions as well. By a simple membrane analysis (SI Appendix, section 2), we found that for the limiting case with no sliding at the edge, that is, the strong shear limit for the membrane–substrate interface; is the Poisson’s ratio of the membrane material. Alternatively, is predicted for the weak shear limit when the membrane–substrate interface is essentially frictionless. In this case, the elastic energy in the membrane is reduced by sliding. Compared with the strong shear limit, the weak shear limit predicts a larger aspect ratio for the blister, about 20% higher for graphene () in particular.
To further examine the effect of a finite interfacial shear stress on the aspect ratio of the blisters, we performed a more rigorous analysis for the liquid-filled blisters following Hencky’s approach (31, 40). Assuming a finite interfacial shear stress () between the membrane and the substrate, an annular sliding zone () develops outside the edge of a circular blister where ρ is a dimensionless coefficient. The blister radius () and the extent of the sliding zone () are both determined by minimizing the total free energy under the condition of a constant liquid volume. For a given liquid volume (), we define a length scale as . The normalized blister radius () can be obtained as a function of three dimensionless parameters: , and . The aspect ratio () can also be derived (SI Appendix, Eq. S30). It is found that, for a membrane–substrate interface with or , the aspect ratio of the blister agrees closely with the predictions by Eq. 4 for the strong shear or the weak shear limit, respectively, especially under small deflection (SI Appendix, Fig. S8). In reality, for most 2D membranes, including graphene on SiO2, the interfacial shear stress is fairly small as summarized in SI Appendix, Table S1. The weak shear limit can be used as a good approximation as long as the liquid volume in the blister or the aspect ratio is relatively small ( nm or ). Moreover, considering the finite lateral size of the membrane (SI Appendix, Fig. S9), the Hencky’s analysis is slightly modified to account for the boundary conditions (more details in SI Appendix, section 2), with which we find that the finite size effect is typically negligible as long as the blister is not located close to the edge of a membrane (allowing ).
MD Simulations.
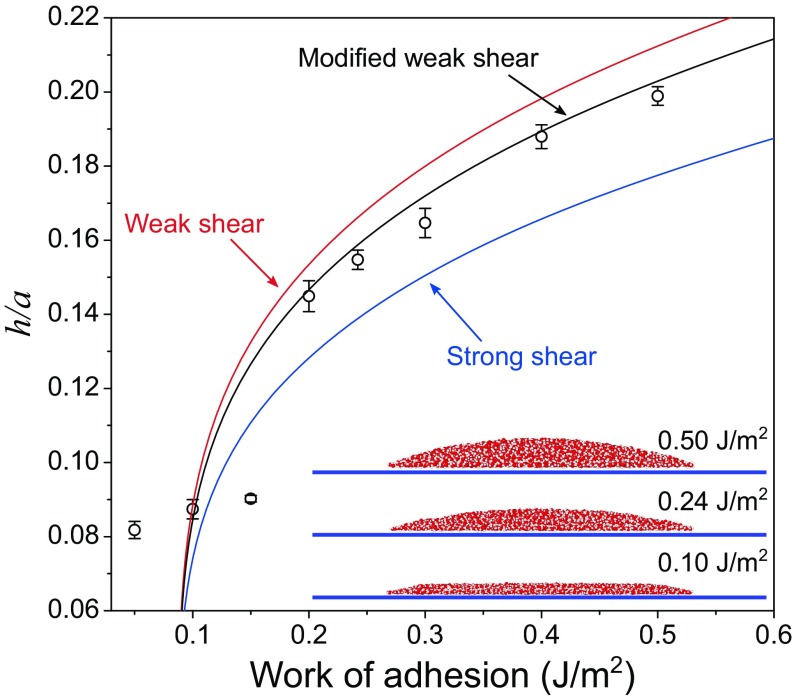
As a verification for our analytical model, MD simulations were conducted to simulate water-filled blisters trapped between a monolayer graphene membrane and a rigid substrate (see SI Appendix, section 3 for details). As predicted by Eq. 4, the aspect ratio of the blister depends on the graphene-to-substrate adhesion energy (Γ) and the two water contact angles ( and ). For the MD simulations, we set to be 60° and to be 40° by selecting proper parameters for the interaction potentials between water and graphene and between water and the substrate. The interaction parameters between graphene and the substrate are varied to simulate graphene blisters with different aspect ratios as a result of different adhesion energy Γ. It is noted that it may not be possible to fully capture the mechanics, wetting, and surface chemistry by using the empirical force fields in the present study. Fig. 3 plots the MD results in comparison with the analytical predictions, along with three snapshots for the trapped water molecules (n = 2,700). When the adhesion energy is relatively large (Γ > 0.2 J/m2), the water molecules take the shape of a spherical cap as assumed in the continuum model. In this case, the aspect ratio increases with increasing adhesion energy, in close agreement with the analytical prediction assuming a frictionless interface. As expected, the results are bounded by the strong shear limit [] and the weak shear limit () for an infinitely large membrane. The weak shear limit overestimates the aspect ratio in MD due to the periodic boundary conditions employed in the MD simulations, and the strong shear limit underestimates the aspect ratio due to the assumption of no sliding. Interestingly, for the case of a lower adhesion energy (Γ < 0.2 J/m2), the top of the blister is nearly flat, and the water molecules form a distinct bilayer structure instead of a spherical cap. As a result, the continuum assumption breaks down, and the aspect ratio becomes nearly independent of the adhesion energy for the same number of water molecules (n = 2,700). It is found that the breakdown of the continuum model depends on the adhesion energy (Γ) and the number of water molecules (n). As shown in SI Appendix, Fig. S13, for Γ = 0.242 J/m2 the continuum model remains applicable for n > 1,600. However, for Γ = 0.1 J/m2, our MD simulations predict a bilayer water structure for n up to 4,500. Hence, for n < 4,500 as limited by the computational cost of MD simulations, we could not simulate a graphene blister in the continuum regime for Γ = 0.1 J/m2. Nevertheless, the analytical prediction based on the continuum model is confirmed by the MD simulations for the cases when the adhesion energy and the number of water molecules combine to yield a blister in the shape of a spherical cap, such as Γ > 0.2 J/m2 and n = 2,700 in Fig. 3.
Fig. 3.
Modeling and MD simulations of water-filled blisters. MD simulation results (circular markers) best agree with our simplified model assuming a frictionless, sliding interface (modified weak shear). The deviations, especially under small height or aspect ratio, are attributed to the size limitation of MD, which can induce discrete behaviors. (Inset) The figure demonstrates how the shape of the blister changes for different values of the work of adhesion.
Discussion and Conclusions
Having verified our theoretical analysis with MD simulations, we now apply the model to experimentally measured aspect ratio data to extract the adhesion energy for a variety of 2D material interfaces, as well as elaborate on the implications of the data for 2D material systems.
Adhesion Energy for 2D Material Interfaces.
The family of 2D materials has grown appreciably in recent years (1, 2). The emergence of each new material brings demands for exploring its vdW interactions with various types of substrates and 2D materials, as many exciting applications of these materials come from stacking them into multilayers and heterostructures. Because of the significance of vdW interactions, many experimental studies have been carried out to measure the adhesion energy of 2D material interfaces, e.g., pressurized blister (8), buckling-based metrology (41–43), and double-cantilever method (44, 45), as summarized in recent review papers (3, 46). However, it is tedious or impossible to determine the adhesion energy for every pair of 2D material interfaces. Based on the present work, we propose that adhesion energy of a 2D material interface can be readily estimated by measuring the aspect ratio of spontaneously formed nanoblisters (if present). To calculate the adhesion energy, Eq. 4 is rewritten as
| [5] |
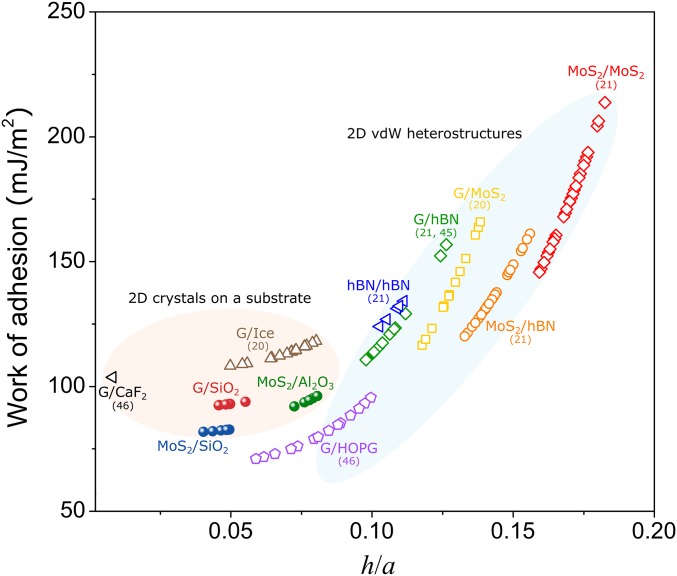
which suggests that once the relevant material properties are available, the adhesion energy can be determined by just measuring the aspect ratio of a blister. We take by the weak interface model due to the typically weak interfacial shear resistance for most of 2D material interfaces (SI Appendix, Table S1). Note that the strong interface model gives a smaller prefactor (), thus overestimating the adhesion energy. Assuming water is trapped in the blisters, in Fig. 4, we calculated the graphene–SiO2, MoS2–SiO2, and MoS2–Al2O3 work of adhesion by using our measurements in Fig. 1. Our values are in reasonable agreement with values determined in similar systems via alternative methods (0.1–0.4 J/m2 for graphene–SiO2 and 0.04 J/m2 for MoS2–SiO2) (32, 47, 48). We attribute our slightly lower adhesion values to: (i) previously neglected, but significant, interfacial sliding; (ii) the slight amount of contaminants which can influence the surface tension and contact angle terms for water in Eq. 3; and (iii) the rough substrate surface (197 ± 19 pm in our sample) which is believed to cause scattering in adhesion measurements with SiO2 (8). For our Al2O3 substrate, the surface roughness was measured to be 251 ± 10 pm. Notably, nanoblisters found in our samples often exhibit some degree of ellipticity (SI Appendix, Fig. S2). Therefore, only approximately circular blisters with minor-to-major axis ratios larger than 0.85 are used for the adhesion energy calculations. The resulting uncertainty in adhesion energy is calculated to be at most 1, 1, and 5 mJ/m2 for graphene–SiO2, MoS2–SiO2, and MoS2–Al2O3 interfaces, respectively.
Fig. 4.
Work of adhesion values for various 2D material interfaces estimated according to blister profiles, including many interfaces found in 2D heterostructures. Solid markers indicate our own experiments while open markers are for blisters reported in the literature.
We further provide a survey of the relevant parameters from several studies of water-filled blisters in the literature (13, 20, 49). The material properties used in adhesion energy calculations are summarized in SI Appendix, section 4. By substituting these values into Eq. 5, we are able to estimate the interfacial adhesion energies for a variety of interfaces (Fig. 4, also summarized in Table 1). If the affinity between the 2D crystal and its substrate is smaller than the affinity of the 2D crystal to the entrapped liquid, then the energetically favorable configuration should be the one that maximizes the contact between the 2D crystal and the liquid. To achieve this configuration, the liquid would spread out and form a layered, ice-like structure with almost zero h/a. Our model can hence predict an upper limit for the adhesion energy of these 2D material interfaces as (noted as the yellow region in Table 1). This simple relation also quantitatively offers a criterion for the interesting observation of room-temperature ice formation in a 2D nanochannel (50–56). This formula can also help explain the so-called self-cleaning mechanism (formation of blisters) which is typically observed at atomically smooth, hydrophobic 2D heterostructure interfaces such as graphene–V2O5 (9).
Table 1.
Estimation of adhesion energy via blister profiles
| Interface type | Materials (ref) | Adhesion energy (mJ/m2) |
| 2D crystal vdW heterostructures | MoS2–MoS2 (13) | 174 ± 18 |
| G–MoS2 (20) | 140 ± 26 | |
| MoS2–hBN (13) | 136 ± 11 | |
| hBN–hBN (13) | 129 ± 4 | |
| G–hBN (13, 49) | 126 ± 20 | |
| G–HOPG (22) | 86 ± 16 | |
| 2D crystal on a substrate | G-Ice (20) | 124 ± 30 |
| G–CaF2 (28) | 104 | |
| MoS2–Al2O3* | 101 ± 15 | |
| G–SiO2* | 93 ± 1 | |
| MoS2–SiO2* | 82 ± 1 | |
| Graphene interfaces without blisters | G–V2O5 (9) | ≤108 |
| G–sapphire (50) | ≤107 | |
| G–Mica (51–54) | ≤102 | |
| G–Si (55) | ≤72 | |
| G–SiC (56) | ≤57 |
Knowing the adhesion values of various vdW interfaces of 2D crystals is very beneficial to the fabrication of 2D crystal-based devices. The fabrication typically involves either exfoliation of 2D layers from bulk crystal or transfer of synthesized 2D crystals from a donor substrate to a target substrate. Such processes rely on the competing adhesion energies between the 2D crystal and its “stamp,” and the various surfaces that it contacts. For example, Brennan et al. (43) reported the adhesion of MoS2 to polydimethylsiloxane is 18 ± 2 mJ/m2, which is relatively weak compared with the adhesion between MoS2 and SiO2, or MoS2 and graphene, as estimated in Fig. 4. As a result, delivering 2D MoS2 to those substrates from an elastomeric stamp is mechanically viable (57–60). Therefore, the adhesion energy values obtained by our blister metrology (Fig. 4) can help guide and optimize the transfer of 2D materials.
Implications for Applications of 2D Material Blisters.
We conclude by highlighting some of the implications of our work for the applications of 2D material blisters. In addition to adhesion energy, our liquid-filled blister model can also predict the confinement pressure, , inside the blisters and the strain distribution in the 2D membrane. The confinement pressure was previously estimated by capturing pressure-sensitive molecules trapped inside the blister, studying molecular structural and conformational changes, and observing the specific chemistry inside the blister (17, 19). Our model offers a direct relation between the confinement pressure and the geometry of the blisters (SI Appendix, section 2), namely
| [6] |
where for a graphene blister with a strong shear interface and for a weak shear interface. Note that unlike the adhesion energy, which only depends on the aspect ratio of the blister, the confinement pressure given in Eq. 6 depends on the size of the blister and has to be estimated with both the height and radius known. For a particular 2D material and interface, the aspect ratio (h/a) is a constant and the confining pressure is inversely proportional to the blister radius. For the water-filled nanoblisters confined between MoS2 and Al2O3 in our experiment (e.g., h = 4 nm, a = 50 nm), we estimate the confinement pressure to be around 7 MPa. Note that the strain distribution in the blisters can also be estimated based on our analysis (Eqs. S4 and S5 in SI Appendix, section 2).
Furthermore, in applications of 2D material blisters it is vital that the blister shape and confinement conditions can be controlled. Eq. 3 provides a direct guidance to the aspect ratio of the blisters. For a given interface with fixed adhesion, trapping different types of liquids with different surface energies and contact angles can tune the blister shape and membrane strain. In fact, a recent study by Neek-Amal and coworkers (12) demostrated the dependence of the shape of graphene nanoblisters on trapped substance. Our proposed strategies are also consistent with our MD simulations in Fig. 3.
Materials and Methods
The monolayer graphene and MoS2 samples were mechanically exfoliated from their respective bulk crystals onto a 300-nm SiO2/Si substrate. The MoS2–Al2O3 sample fabrication and characterization details are in a previous work (60). Further detail is provided in SI Appendix, section 1.
Supplementary Material
Acknowledgments
Z.D. acknowledges the Warren A. and Alice L. Meyer Endowed Scholarship in Engineering. N.L. and D.A.S. thank Prof. Xiaoqin Li and Mr. Kha Tran [The University of Texas at Austin (UT Austin)] for the discussions about exfoliating and transferring 2D materials. D.A.S. acknowledges Dr. Raluca Gearba and Dr. Andrei Dolocan (UT Austin) for their assistance in using the Texas Material Institute facilities. This work is supported by the NSF Division of Civil, Mechanical and Manufacturing Innovation (CMMI) under Grants 1351875 and 1562820. D.A.S. acknowledges support from the NSF Graduate Research Fellowship Program; the Graduate Education for Minorities Fellowship; the T. W. Whaley, Jr. Friends of Alec Endowed Scholarship of the NSF Nanosystems Engineering Research Center (NERC) for Nanomanufacturing Systems for Mobile Computing and Mobile Energy Technologies (NASCENT); and the Virginia and Ernest Cockrell, Jr. Fellowship of UT Austin.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1801551115/-/DCSupplemental.
References
- 1.Novoselov KS, Mishchenko A, Carvalho A, Castro Neto AH. 2D materials and van der Waals heterostructures. Science. 2016;353:aac9439. doi: 10.1126/science.aac9439. [DOI] [PubMed] [Google Scholar]
- 2.Geim AK, Grigorieva IV. Van der Waals heterostructures. Nature. 2013;499:419–425. doi: 10.1038/nature12385. [DOI] [PubMed] [Google Scholar]
- 3.Akinwande D, et al. A review on mechanics and mechanical properties of 2D materials—Graphene and beyond. Extreme Mech Lett. 2017;13:42–77. [Google Scholar]
- 4.Klimov NN, et al. Electromechanical properties of graphene drumheads. Science. 2012;336:1557–1561. doi: 10.1126/science.1220335. [DOI] [PubMed] [Google Scholar]
- 5.Levy N, et al. Strain-induced pseudo-magnetic fields greater than 300 tesla in graphene nanobubbles. Science. 2010;329:544–547. doi: 10.1126/science.1191700. [DOI] [PubMed] [Google Scholar]
- 6.Koren E, Lörtscher E, Rawlings C, Knoll AW, Duerig U. Surface science. Adhesion and friction in mesoscopic graphite contacts. Science. 2015;348:679–683. doi: 10.1126/science.aaa4157. [DOI] [PubMed] [Google Scholar]
- 7.Kitt AL, et al. How graphene slides: Measurement and theory of strain-dependent frictional forces between graphene and SiO2. Nano Lett. 2013;13:2605–2610. doi: 10.1021/nl4007112. [DOI] [PubMed] [Google Scholar]
- 8.Koenig SP, Boddeti NG, Dunn ML, Bunch JS. Ultrastrong adhesion of graphene membranes. Nat Nanotechnol. 2011;6:543–546. doi: 10.1038/nnano.2011.123. [DOI] [PubMed] [Google Scholar]
- 9.Kretinin AV, et al. Electronic properties of graphene encapsulated with different two-dimensional atomic crystals. Nano Lett. 2014;14:3270–3276. doi: 10.1021/nl5006542. [DOI] [PubMed] [Google Scholar]
- 10.Pizzocchero F, et al. The hot pick-up technique for batch assembly of van der Waals heterostructures. Nat Commun. 2016;7:11894. doi: 10.1038/ncomms11894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lloyd D, et al. Band gap engineering with ultralarge biaxial strains in suspended monolayer MoS2. Nano Lett. 2016;16:5836–5841. doi: 10.1021/acs.nanolett.6b02615. [DOI] [PubMed] [Google Scholar]
- 12.Ghorbanfekr-Kalashami H, Vasu KS, Nair RR, Peeters FM, Neek-Amal M. Dependence of the shape of graphene nanobubbles on trapped substance. Nat Commun. 2017;8:15844. doi: 10.1038/ncomms15844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Khestanova E, Guinea F, Fumagalli L, Geim AK, Grigorieva IV. Universal shape and pressure inside bubbles appearing in van der Waals heterostructures. Nat Commun. 2016;7:12587. doi: 10.1038/ncomms12587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chen Z, et al. Interface confined hydrogen evolution reaction in zero valent metal nanoparticles-intercalated molybdenum disulfide. Nat Commun. 2017;8:14548. doi: 10.1038/ncomms14548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lim CHYX, et al. A hydrothermal anvil made of graphene nanobubbles on diamond. Nat Commun. 2013;4:1556. doi: 10.1038/ncomms2579. [DOI] [PubMed] [Google Scholar]
- 16.Lu J, Neto AH, Loh KP. Transforming Moiré blisters into geometric graphene nano-bubbles. Nat Commun. 2012;3:823. doi: 10.1038/ncomms1818. [DOI] [PubMed] [Google Scholar]
- 17.Vasu KS, et al. Van der Waals pressure and its effect on trapped interlayer molecules. Nat Commun. 2016;7:12168. doi: 10.1038/ncomms12168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zamborlini G, et al. Nanobubbles at GPa pressure under graphene. Nano Lett. 2015;15:6162–6169. doi: 10.1021/acs.nanolett.5b02475. [DOI] [PubMed] [Google Scholar]
- 19.Lim CHYX, Nesladek M, Loh KP. Observing high-pressure chemistry in graphene bubbles. Angew Chem Int Ed Engl. 2014;53:215–219. doi: 10.1002/anie.201308682. [DOI] [PubMed] [Google Scholar]
- 20.Bampoulis P, Teernstra VJ, Lohse D, Zandvliet HJ, Poelsema B. Hydrophobic ice confined between graphene and MoS2. J Phys Chem C. 2016;120:27079–27084. [Google Scholar]
- 21.Haigh SJ, et al. Cross-sectional imaging of individual layers and buried interfaces of graphene-based heterostructures and superlattices. Nat Mater. 2012;11:764–767. doi: 10.1038/nmat3386. [DOI] [PubMed] [Google Scholar]
- 22.Cao P, Xu K, Varghese JO, Heath JR. The microscopic structure of adsorbed water on hydrophobic surfaces under ambient conditions. Nano Lett. 2011;11:5581–5586. doi: 10.1021/nl2036639. [DOI] [PubMed] [Google Scholar]
- 23.Yue K, Gao W, Huang R, Liechti KM. Analytical methods for the mechanics of graphene blisters. J Appl Phys. 2012;112:083512. [Google Scholar]
- 24.An H, et al. Graphene nanobubbles produced by water splitting. Nano Lett. 2017;17:2833–2838. doi: 10.1021/acs.nanolett.6b05183. [DOI] [PubMed] [Google Scholar]
- 25.Falin A, et al. Mechanical properties of atomically thin boron nitride and the role of interlayer interactions. Nat Commun. 2017;8:15815. doi: 10.1038/ncomms15815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Huang Y, et al. Reliable exfoliation of large-area high-quality flakes of graphene and other two-dimensional materials. ACS Nano. 2015;9:10612–10620. doi: 10.1021/acsnano.5b04258. [DOI] [PubMed] [Google Scholar]
- 27.Ferrari AC, et al. Raman spectrum of graphene and graphene layers. Phys Rev Lett. 2006;97:187401. doi: 10.1103/PhysRevLett.97.187401. [DOI] [PubMed] [Google Scholar]
- 28.Temmen M, Ochedowski O, Schleberger M, Reichling M, Bollmann T. Hydration layers trapped between graphene and a hydrophilic substrate. New J Phys. 2014;16:053039. [Google Scholar]
- 29.Wang P, Gao W, Cao Z, Liechti KM, Huang R. Numerical analysis of circular graphene blisters. J Appl Mech. 2013;80:040905. [Google Scholar]
- 30.Drahushuk LW, Wang L, Koenig SP, Bunch JS, Strano MS. Analysis of time-varying, stochastic gas transport through graphene membranes. ACS Nano. 2016;10:786–795. doi: 10.1021/acsnano.5b05870. [DOI] [PubMed] [Google Scholar]
- 31.Wang G, et al. Measuring interlayer shear stress in bilayer graphene. Phys Rev Lett. 2017;119:036101. doi: 10.1103/PhysRevLett.119.036101. [DOI] [PubMed] [Google Scholar]
- 32.Boddeti NG, et al. Graphene blisters with switchable shapes controlled by pressure and adhesion. Nano Lett. 2013;13:6216–6221. doi: 10.1021/nl4036324. [DOI] [PubMed] [Google Scholar]
- 33.Berry V. Impermeability of graphene and its applications. Carbon. 2013;62:1–10. [Google Scholar]
- 34.Ahmadpoor F, Wang P, Huang R, Sharma P. Thermal fluctuations and effective bending stiffness of elastic thin sheets and graphene: A nonlinear analysis. J Mech Phys Solids. 2017;107:294–319. [Google Scholar]
- 35.Gao W, Huang R. Thermomechanics of monolayer graphene: Rippling, thermal expansion and elasticity. J Mech Phys Solids. 2014;66:42–58. [Google Scholar]
- 36.Lee C, Wei X, Kysar JW, Hone J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science. 2008;321:385–388. doi: 10.1126/science.1157996. [DOI] [PubMed] [Google Scholar]
- 37.Israelachvili J. Intermolecular and Surface Forces. 2nd Ed Academic; London: 1991. [Google Scholar]
- 38.Rafiee J, et al. Wetting transparency of graphene. Nat Mater. 2012;11:217–222. doi: 10.1038/nmat3228. [DOI] [PubMed] [Google Scholar]
- 39.Seemann R, Herminghaus S, Jacobs K. Dewetting patterns and molecular forces: A reconciliation. Phys Rev Lett. 2001;86:5534–5537. doi: 10.1103/PhysRevLett.86.5534. [DOI] [PubMed] [Google Scholar]
- 40.Fichter WB. 1997. Some solutions for the large deflections of uniformly loaded circular membranes (National Aeronautics and Space Administration, Langley Research Center, Hampton, VA), NASA Technical Paper 3658.
- 41.Jiang T, Huang R, Zhu Y. Interfacial sliding and buckling of monolayer graphene on a stretchable substrate. Adv Funct Mater. 2013;24:396–402. [Google Scholar]
- 42.Dai Z, et al. Mechanical behavior and properties of hydrogen bonded graphene/polymer nano-interfaces. Compos Sci Technol. 2016;136:1–9. [Google Scholar]
- 43.Brennan CJ, Nguyen J, Yu ET, Lu N. Interface adhesion between 2D materials and elastomers measured by buckle delaminations. Adv Mater Interfaces. 2015;2:1500176. [Google Scholar]
- 44.Yoon T, et al. Direct measurement of adhesion energy of monolayer graphene as-grown on copper and its application to renewable transfer process. Nano Lett. 2012;12:1448–1452. doi: 10.1021/nl204123h. [DOI] [PubMed] [Google Scholar]
- 45.Na SR, Suk JW, Ruoff RS, Huang R, Liechti KM. Ultra long-range interactions between large area graphene and silicon. ACS Nano. 2014;8:11234–11242. doi: 10.1021/nn503624f. [DOI] [PubMed] [Google Scholar]
- 46.Bunch JS, Dunn ML. Adhesion mechanics of graphene membranes. Solid State Commun. 2012;152:1359–1364. [Google Scholar]
- 47.Lloyd D, et al. Adhesion, stiffness, and instability in atomically thin MoS2 bubbles. Nano Lett. 2017;17:5329–5334. doi: 10.1021/acs.nanolett.7b01735. [DOI] [PubMed] [Google Scholar]
- 48.Zong Z, Chen C-L, Dokmeci MR, Wan K-t. Direct measurement of graphene adhesion on silicon surface by intercalation of nanoparticles. J Appl Phys. 2010;107:026104. [Google Scholar]
- 49.Uwanno T, Hattori Y, Taniguchi T, Watanabe K, Nagashio K. Fully dry PMMA transfer of graphene on h-BN using a heating/cooling system. 2D Mater. 2015;2:041002. [Google Scholar]
- 50.Komurasaki H, Tsukamoto T, Yamazaki K, Ogino T. Layered structures of interfacial water and their effects on Raman spectra in graphene-on-sapphire systems. J Phys Chem C. 2012;116:10084–10089. [Google Scholar]
- 51.He KT, Wood JD, Doidge GP, Pop E, Lyding JW. Scanning tunneling microscopy study and nanomanipulation of graphene-coated water on mica. Nano Lett. 2012;12:2665–2672. doi: 10.1021/nl202613t. [DOI] [PubMed] [Google Scholar]
- 52.Shim J, et al. Water-gated charge doping of graphene induced by mica substrates. Nano Lett. 2012;12:648–654. doi: 10.1021/nl2034317. [DOI] [PubMed] [Google Scholar]
- 53.Ochedowski O, Bussmann BK, Schleberger M. Graphene on mica–Intercalated water trapped for life. Sci Rep. 2014;4:6003. doi: 10.1038/srep06003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Xu K, Cao P, Heath JR. Graphene visualizes the first water adlayers on mica at ambient conditions. Science. 2010;329:1188–1191. doi: 10.1126/science.1192907. [DOI] [PubMed] [Google Scholar]
- 55.Gowthami T, Tamilselvi G, Jacob G, Raina G. The role of ambient ice-like water adlayers formed at the interfaces of graphene on hydrophobic and hydrophilic substrates probed using scanning probe microscopy. Phys Chem Chem Phys. 2015;17:13964–13972. doi: 10.1039/c5cp01703c. [DOI] [PubMed] [Google Scholar]
- 56.Kazakova O, Panchal V, Burnett TL. Epitaxial graphene and graphene–based devices studied by electrical scanning probe microscopy. Crystals (Basel) 2013;3:191–233. [Google Scholar]
- 57.Wang G, et al. Biaxial compressive behavior of embedded monolayer graphene inside flexible poly (methyl methacrylate) matrix. Carbon. 2015;86:69–77. [Google Scholar]
- 58.Wang G, et al. Tuning the interfacial mechanical behaviors of monolayer graphene/PMMA nanocomposites. ACS Appl Mater Interfaces. 2016;8:22554–22562. doi: 10.1021/acsami.6b03069. [DOI] [PubMed] [Google Scholar]
- 59.Wang G, et al. Degradation and recovery of graphene/polymer interfaces under cyclic mechanical loading. Compos Sci Technol. 2017;149:220–227. [Google Scholar]
- 60.Brennan CJ, et al. Out-of-plane electromechanical response of monolayer molybdenum disulfide measured by piezoresponse force microscopy. Nano Lett. 2017;17:5464–5471. doi: 10.1021/acs.nanolett.7b02123. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.