Fig. 4. Emergent electromagnetic fields for dynamically generated deformed skyrmion strings.

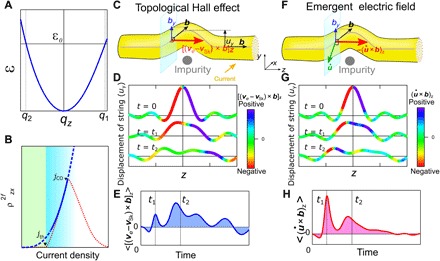
(A) Dispersion relation of the low-energy excitation (ε) of SkL with a propagating vector along the external magnetic field direction (q_z). (B) Schematic for the current dependence of nonreciprocal nonlinear (second-harmonic) Hall resistivity. The solid blue line represents the theoretical calculation, which is valid for the current density between j_th and j_CO, and the broken blue line denotes the square of the current density and is simply a guide to the eyes. The red line indicates the experimentally observed current profile (see also Fig. 3B). (C and F) Schematics of emergent electromagnetic fields for the deformation of a skyrmion string when it collides with point-like impurity. u represents the displacement vector of a skyrmion string. The red arrows denote the z components of the topological Hall electric field [(v_e − v_Sk) × b]_z (C) and the emergent electric field ${\mathit{e}}_{\mathit{z}}=-{[\widehat{\mathbf{u}}\times \mathbf{b}]}_{\mathit{z}}$ (F). (D and G) Position (z) dependence of the displacement of skyrmion strings shown together with the color map of the z components of both (v_e − v_Sk) × b (D) and $\mathit{e}=-\widehat{\mathbf{u}}\times \mathbf{b}$ (G) at several time points. (E and H) Time dependence of the average z components of both (v_e − v_Sk) × b (E) and $\mathbf{e}=-\widehat{\mathbf{u}}\times \mathbf{b}$ (H) over the skyrmion string.