An assessment of the effectiveness of virginiamycin on liver abscess incidence and growth performance in feedlot cattle: a comprehensive statistical analysis

Abstract

The judicious use of commercial products in livestock operations can be part of a sustainable and environmentally friendly production scenario. This study was designed to gather published data of virginiamycin (VM) used in feedlot conditions of the United States and analyze its effectiveness and optimum dosage in reducing the liver abscess incidence (LAI). The dataset contained 26 studies that evaluated more than 7,156 animals of diverse breeds fed in several regions in the United States under different management. Statistical analyses included contingency tables to assess the nonparametric independence of the LAI, meta regression analysis to remove study effects and to evaluate LAI and animal performance, broken-line analysis to determine thresholds of VM dosage on LAI, and residual-based shading mosaic plots to illustrate the contingency analysis. There were 1,391 of 5,430 animals with LAI scores 1, 2, or 3 (LAI_1–3) and 651 of 4,690 animals with LAI A+ (score 3). Our analyses suggested that there was a significant dependency (χ²P-value < 0.001) and significant asymmetry (McNemar’s test P-value < 0.001) between LAI and VM treatment for both LAI_1–3 and LAI A+. For the LAI_1–3 group, only 22.5% of the treated animals had liver abscesses compared with 31.7% of the control animals. The metaregression analysis indicated that LAI_1–3 was linearly reduced (P < 0.001) by about 0.42% per mg/kg of DM of VM. The lower 95% confidence interval of the intercept for LAI_1–3 and LAI A+ obtained with a generalized nonlinear mixed regression was 18.7 and 20.3 mg/kg of DM, respectively. The broken-line regression analysis identified 2 thresholds for LAI (23.9 and 12.3 mg/kg of DM) at which the reduction in total LAI_1–3 and LAI A+, respectively, would decrease faster as VM dosage increases (from 2.14% to 6% and from 1.91% to 4.33% per mg of VM per kg of DM, respectively). Additionally, our analyses indicated that after accounting for the study effects, VM significantly increased ADG at 2.08 g BW/d per mg/kg DM compared with 0.92 g BW/d per mg/kg DM for monensin (P < 0.001), suggesting that VM was about 2.3 times more effective in increasing ADG for the same dosage and feeding period length. All analyses yielded consistent results that led us to conclude that VM is effective in reducing LAI when fed between approximately 12 and 24 mg/kg of DM, and the maximum reduction might occur at approximately 24 mg/kg of DM or higher.

INTRODUCTION

Within the sustainable production concept, the judicious use of feed additives in livestock production is necessary not only to maximize productivity, but also to improve animal welfare and health, and to reduce environmental contamination (Bartelt-Hunt et al., 2012). The benefits of ionophores and growth-enhancing antibiotics to the livestock industry have been stablished for a long time (Nagaraja, 1995; Tedeschi et al., 2003). Corpet (2000) indicated that growth-enhancing antibiotics might reduce the concentration of ammonia and toxic amines in the gut, consequently reducing the release of N and methane in the environment because of a shift in the gut microflora that alters the microbial population to one that produces a greater proportion of propionate rather than acetate. Virginiamycin (VM) appears to depress the deamination activity of the protein in the rumen (Ives et al., 2002), possibly leading to greater MP supply to the host animal, improving their growth. It is a composite peptolide antibiotic comprising 2 major factors (M and S) that have antimicrobial properties against Gram-positive bacteria in the gut (Gottschall et al., 1988). Monensin (MO) is an ionophore that is also highly effective against Gram-positive bacteria, but likely has a different mode of action (Schelling, 1984; Russell and Strobel, 1989; Nagaraja, 1995). VM is the product of fermentation by a mutant of Streptomyces virginiae (Gottschall et al., 1987) that has proven beneficial properties to ruminants: 1) reduces the incidence of liver abscess due to the inhibition of the growth of ruminal Fusobacterium necrophorum (Nagaraja and Chengappa, 1998) and Actinomyces pyogenes (Narayanan et al., 1998); 2) concomitantly increase in the animal growth due to an effective reduction in lactate and a possible increase in propionate concentrations in the rumen (Nagaraja et al., 1987); and 3) sparing ruminal protein from deamination (Ives et al., 2002). The objective of this paper was to evaluate the effectiveness of VM at controlling liver abscesses and enhance animal growth under feedlot conditions in the United States and to identify possible administration thresholds with a greater likelihood to positively affect welfare and health of cattle.

MATERIALS AND METHODS

Data used in the analyses reported in this paper were summarized from experiments supplementing VM or MO to cattle and published in diverse venues; therefore, the authors conducting this research used no live animal.

Description of the Database

A comprehensive literature search was conducted to collect performance and health data of animals treated with MO, MO plus tylosin, or VM under feedlot conditions in the United States that had animal performance and liver abscess data. Based on the definitions of efficacy and effectiveness trials in experimentation (Gartlehner et al., 2006; Singal et al., 2014), some studies were conducted under ideal circumstances to assess the efficacy of these products, whereas other studies evaluated their effectiveness under real-world conditions. Because no distinction was made between efficacy and effectiveness trials, we adopted the effectiveness nomenclature for analyses. Not all studies indicated the administration (or not) of tylosin in conjunction with MO, but because this is a common feedlot practice of feeding them together in the United States, we assumed that tylosin was always included with MO. The liver abscess incidence (LAI) at the slaughter was recorded using the following notation: A− (or score 1: LAI₁) when 1 or 2 small, well-organized inactive abscesses less than 0.5 mm in diameter; A (or score 2: LAI₂) when 2 to 4 well-organized abscesses without inflammation; A+ (score 3: LAI₃) when 1 or more active liver abscesses with inflammation; and total number of liver abscesses (sum of scores 1, 2, and 3: LAI_1–3). Twenty-six studies were identified, but not all studies fed VM and MO to different groups of animals for complete comparison purposes. Studies 1 to 18 were obtained from the SmithKline V-Max Technical Manual (SmithKline Beecham Animal Health) from which some were published (10 = Bartle et al., 1991; 18 = Gill et al., 1989; 16 = Gill et al., 1990; 1, 2, 3, 4, 5, 6, and 15 = Rogers et al., 1995; 6 = Smith et al., 1989). Seven more published studies (26 = Jim et al., 2017; 23 = Lemos et al., 2016; 21 = Montano et al., 2014; 24 = Navarrete et al., 2017; 19 = Parigi-Bini, 1979; 20 = Salinas-Chavira et al., 2009; 22 = Salinas-Chavira et al., 2016) and 1 unpublished study (25 = Richard A. Zinn, personal communication) were combined with the SmithKline studies. Table 1 has specific differences among studies used to develop the database, which represents more than 7,156 feedlot-fed steers and heifers. Different breeds were used, but most of the studies used English and Continental crossbreds, and few purebreds of Angus, Brahman, Charolais, Friesian, Hereford, Limousin, Nellore, Salers, Shorthorn, and Simmental breeds. The initial BW varied from 117 to 448 kg, whereas the final BW varied from 375 to 670 kg, and animals were fed from 100 up to 342 d.

Table 1.

Characteristics of the studies used to develop the database

Study	Ref.1	Sex2	Breeds3	Additives (doses, mg/kg DM)4	n	DOF	iBW	fBW
1	A	ST	AN, HE, ANxHE	C, VM (10, 25, 50)	790	245	217	477
2	A	ST	ANxHE	C, VM (6.6, 8.9, 13.6)	190	109	390	586
3	A	ST	BR	C, VM (11, 19.3, 27.6)	280	168	301	521
4	A	ST	HE, CHxHExSH	C, VM (11, 19.3, 27.6)	395	141	341	509
5	A	ST/HF	CH, CHx/ANx, HEx, LIx, BRx, SIx	C, VM (11, 19.3, 27.6)	399	120	325	504
6	B	ST	ANx, HEx, LIx, BRx, SIx	C, VM (11, 19.3, 27.6)	318	141	313	545
7	C	ST	AN, HE, ANxHE	C, VM (27.6), MO (27.6)	240	128	344	525
8	C	ST	HE	C, VM (19.3, 27.6), MO (27.6)	387	139	321	550
9	C	ST	AN, HE, ANxHE	C, VM (19.3, 27.6), MO (27.6)	318	138	352	561
10	D	St	ANx, HEx, LIx, BRx, SIx	C, VM (19.3, 20), MO (27.6)	312	156	332	540
11	C	ST	BR	C, VM (23.7), MO (33.8)	298	123	361	589
12	C	ST	ANxHE	C, VM (19.3), MO (27.6)	297	128	341	570
13	C	ST	ANx, HEx, CHx, SIx	C, VM (24.5), MO (27.1)	297	130	302	558
14	C	ST	HEx, SAx,CHx	C, VM (19.3), MO (30.6)	295	111	373	599
15	A	ST	HE	C, VM (11, 19.3, 27.6), MO (27.6)	393	134	310	479
16	E	ST	ANxHE	C, VM (11, 19.3), MO (27.6)	221	140	338	566
17	C	ST	AN, ANxHE	C, VM (11, 19.3), MO (27.6)	254	118	362	566
18	F	ST	ANxHE	C, VM (11), MO (27.6)	200	133	350	585
19	G	BU	FR	C, VM (0, 20, 25, 40, 50)	133	119	251	410
20	H	ST	HO	C, VM (16, 22.5), MO (28)	144	340	119	590
21	I	ST	HExBR, ANxBR, SHxBR, CHxBR	C, VM (26), MO (34)	135	143	314	552
22	J	ST	HO	C, VM (22.5)	120	308	131	575
23	K	BU	NE	VM (25), MO (30)	100	101	392	538
24	L	ST	ND	C, VM (28)	80	152	298	527
25	M	ST	ND	C, VM (22.7)	80	342	131	623
26	N	ST/HF	ND	C, VM (20)	480	152	448	668

n = number of animals in the study; DOF = days on feed; iBW = initial BW, kg; fBW = final BW, kg.

¹References: A = Rogers et al. (1995) and SmithKline V-Max Technical Manual; B = Smith et al. (1989), Rogers et al. (1995), and SmithKline V-Max Technical Manual; C = SmithKline V-Max Technical Manual; D = Bartle et al. (1991) and SmithKline V-Max Technical Manual; E = Gill et al. (1990) and SmithKline V-Max Technical Manual; F = Gill et al. (1989) and SmithKline V-Max Technical Manual; G = Parigi-Bini (1979); H = Salinas-Chavira et al. (2009); I = Montano et al. (2014); J = Salinas-Chavira et al. (2016); K = Lemos et al. (2016); L = Navarrete et al. (2017); M = Richard A. Zinn (personal communication); and N = Jim et al. (2017).

²BU = bulls; HF = heifers; ST = steers.

³AN = Angus; BR = Brahman; CH = Charolais; FR = Friesian; HE = Hereford; LI = Limousin; NE = Nellore; SA = Salers; SH = Shorthorn; SI = Simmental; ND = not defined (most likely crossbreds).

⁴C = control; MO = monensin + tylosin; VM = virginiamycin. Studies may contain additional treatments not listed in this table.

Statistical Analyses

Statistical analyses were conducted with R version 3.4.3 (R Core Team, 2017). Graphics were generated with the plot function or the ggplot2 package of R (Wickham, 2009). The 3-dimensional graphics were developed with Mathematica version 11.2 (Wolfram Research, 2017).

Contingency table analysis.

Contingency tables and the χ² test (Agresti, 2002) were used to conduct nonparametric analyses of the number of animals with and without liver abscesses to total occurrence of liver abscesses (i.e., LAI_1–3) and liver abscesses A+ (i.e., LAI₃). Contingency table analyses were conducted using R version 3.4.3, as described by Horton and Kleinman (2011). The Fisher’s χ² test was used to assess the independence and the McNemar’s χ² test was used to assess the symmetry between treatment (with or without VM) and LAI (with or without liver abscesses). Additionally, the association of the variables in the contingency tables of liver abscess was assessed using the conditional independence test with 5,000 permutation distributions (Zeileis et al., 2007). The odds ratio, using the Fisher’s exact test, was used to evaluate the odds of relative occurrence of liver abscesses and VM treatment. Residual-based shading plots (also known as mosaic displays) were used to graphically represent contingency tables (Hartigan and Kleiner, 1984; Friendly, 1994; Emerson, 1998; Meyer et al., 2006). In the mosaic displays, the area of the cell (square or rectangle) represents the quantities (counts), the cell’s width represents the marginal probability within the row (VM dosage), the cell’s height represents the marginal probability within the column (liver abscess), and the cell’s color intensity represents the deviation from the expected values (i.e., standardized Person residual from independence): positive (blue and solid outline) or negative (red and dashed outline) deviations from expected values at approximately P < 0.001 (darker color) or at P < 0.01 (light color).

Metaregression analysis

The metaregression was conducted with R version 3.4.3 (R Core Team, 2017), assuming random coefficient regression models in which studies were treated as random effects. The sample size for each treatment within the study was used as a weight variable for the ordinary least square (OLS) and generalized least square (GLS) methods. More specifically, for lme and nlme functions of the nlme package for R (Pinheiro et al., 2014), the weights were assigned as the inverse of the sample size (e.g., 1 per sample size). For linear regressions, the parameter estimates were obtained with the generalized linear mixed-effects regressions (Pinheiro and Bates, 2000) using the lme function of the nlme package for R (Pinheiro et al., 2014) with the restricted maximum likelihood (REML) estimation. The unstructured (UN) variance–covariance matrix structure was initially used to determine the influence of study effects, and when the UN did not converge, the variance components (VC) variance–covariance matrix was used. It was assumed that both intercept and slope were affected by the study effect, and then this model was compared with the model without the study effect on the slope. The simpler model was selected based on the anova function comparison of the Akaike’s Information Criteria (AIC). In R, the VC of the random coefficient models (i.e., study and uncontrolled random errors) was estimated using a diagonal positive-definite matrix constructor (i.e., pdDiag). A direct statistical comparison between VM and MO could not be conducted in the metaregression analysis because not all studies had both feed additives tested. Therefore, we compared the intercepts and slopes of their metaregression using the Student’s t-test (equation (1)) and compared with the Student’s t-table assuming the average of degrees of freedom for VM and MO:

$$t\text{-value}=\left({\widehat{\beta }}_{VM}-{\widehat{\beta }}_{MO}\right)/\left(\sqrt{S{E}_{VM}^2+S{E}_{MO}^2}\right)$$ (1)

where β are the parameter estimates for the intercepts or slopes of VM or MO, and SE is the standard error of the estimates.

For nonlinear regressions, the generalized nonlinear mixed-effects regression (Pinheiro and Bates, 2000) was conducted with the nlme function of the nlme package for R version 3.4.3 (Pinheiro et al., 2014) using the REML method to estimate the coefficients a and b of the exponential decay, $Y=a\times e^{-b\times X}$, where e is the Napierian number (i.e., 2.718). Studies were assumed to be random and the variance–covariance matrix for the random effects was obtained with the pdDiag structure, which assumes a diagonal positive-definite matrix. The sample size for each treatment within study was used as a weight variable, similar to that used for the generalized linear mixed regressions. The effect of study was evaluated on the coefficient a and(or) on the exponent b, and the model with the least significant AIC was identified with the anova function and selected to obtain the nonlinear regression.

Variance partitioning

As described by Tedeschi and Fox (2018) and applied by Eisemann and Tedeschi (2016), when the intercept and slope are subjected to study effects, the calculation of the fraction of the total variance associated with study is more complicated because it depends on the levels of the independent variable (i.e., the X variable) (Goldstein et al., 2002). In this case, the variance associated with the study was computed as follows: ${\sigma }_{Study}^2={\sigma }_{int}^2+X^2\times {\sigma }_{slope}^2+2\times X\times Cov(int,slope)$ where X is the independent variable and Cov is the covariance between the random intercept and the random slope. Because ${\sigma }_{Study}^2$ varies with the level of the X variate, we reported the minimum and maximum contributions of the study to the total variance.

Binomial logistic regression

The analysis of the LAI (as fractional proportions) was performed assuming a binomial distribution using a binomial logistic regression with the logit function of the glm package of R version 3.4.3 (Everitt and Hothorn, 2010). The logit function computes the odds ratio (with vs. without liver abscess) (Agresti, 2002). The number of observations (with and without liver abscesses) was used in the weight statement of the glm package. The independent variables were VM dosage and ADG, and their interaction whenever possible.

Broken-line analysis

Broken-line analysis is also known as piecewise, segmented, or multiphased regressions. It is used to identify one or multiple breakpoints by fitting piecewise terms in regression models when response changes occur abruptly. The broken-line analysis was conducted with the segmented package (Muggeo, 2008) of R version 3.4.3, using the binomial logistic (logit function) regression described above. Preliminary analysis of the data failed to converge, indicating a high level of noise in the dataset. Therefore, the number of animals with and without liver abscesses was combined across studies for each VM dosage. Therefore, only one odds ratio of LAI was obtained for each VM dosage. Because the average of the odds ratio across different studies is not correct, for each VM dosage, the number of animals with LAI was summed up across studies, and the number of animals without LAI was summed up across studies. These 2 values were used to compute the odds ratio using the binomial logistic regression (described above) for a given VM dosage. The segmented package uses an iterative method with bootstrapping to estimate the breakpoints (Muggeo, 2003; Muggeo, 2008).

RESULTS AND DISCUSSION

Animal Performance

Metaregression analysis

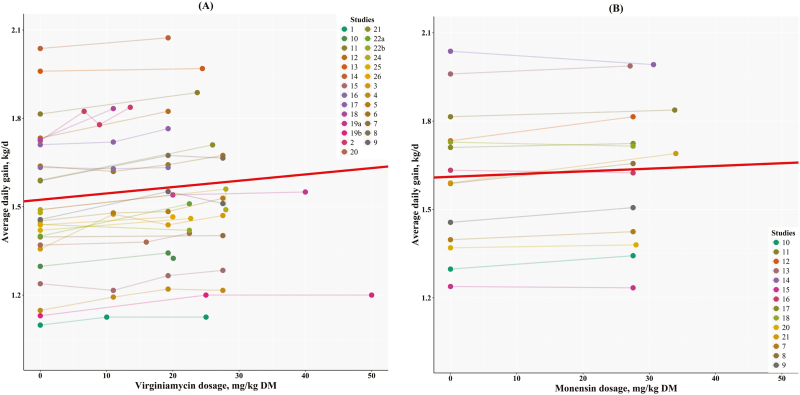
Figure 1 has the generalized linear-mixed regressions adjusted for study effects for ADG on VM dosage (Figure 1A) or MO dosage (Figure 1B). The study variation accounted for between 58.5% and 62.8% of the total variance for VM, and 99.8% for MO. The high contribution of study effect to the total variance in the MO analysis is because most studies only had one dosage of MO, thus, no variance within studies, shifting the majority of the total variance to that of the study effect. The intercept and slope of the metaregression of ADG on MO dosage were still different from zero (P < 0.001). The large contribution of study effects to the total variance is also related to the fact that different studies had different breeds, received different hormonal implants and frequency, were conducted at different locations and seasons, and had different diet ingredients, thus, being true random effects in the overall analysis. The intercepts for these metaregressions for VM and MO differ from zero (P < 0.001), but did not differ between themselves (1.515 vs. 1.611 kg/d, respectively; P = 0.187; Figure 1). Because the intercepts were not different, the base ADG is identical for both treatments. This result was expected because both treatments (VM and MO) had the same control group. In contrast, slopes also differed from zero (P < 0.001), but they were significantly different between themselves (2.08 vs. 0.92 g BW/d per mg/kg DM, respectively; P = 0.018). Therefore, it is expected that VM may yield 2.3 (2.08 ÷ 0.92) times more weight gain than MO when fed at the same dosage for the same feeding period. For example, assuming a dosage of 27.6 mg/kg DM for 100 d, VM is predicted to yield 5.8 kg, whereas MO is predicted to yield 2.5 kg, both more than the control group. Conversely, VM may be fed 2.3 times lower dosage, and the predicted weight gain would be similar to that predicted when compared with feeding MO. Therefore, if MO is fed at 27.6 mg/kg DM, VM could be as effective as MO when fed at 12 mg/kg DM to obtain the same weight gain on average.

Figure 1.

Relationship between ADG and dosage of (A) virginiamycin or (B) monensin. The generalized linear mixed regression (red line) for virginiamycin was Y = 1.515 (±0.00298) + 0.00208 (±0.000159) × X, r² of 0.684, and SE of 0.155, and for monensin it was Y = 1.611 (±0.000011) + 0.00092 (±0.00000054) × X, r² of 0.99 and SE of 0.00036.

Boucque et al. (1990) noticed that a group of Belgian white-red bulls increased ADG by 8% (1.28 to 1.38 kg/d) when fed VM at 25 mg/kg DM, but another group receiving a similar concentrate (but less CP, 18 vs. 14.4 %DM, respectively) did not respond to the treatment (ADG was 1.37 kg/d). The response observed in the first experiment is within the expected performance based on the predictive equation for VM shown in Figure 1A. Their animals were fed 25 mg/kg DM of VM for about 240 d. Assuming the 2.1 g BW/d per mg/kg DM, one would expect an increase in BW of 12.6 kg (2.1 × 25 × 240/1000). They reported a difference in BW of 10 kg (576 vs. 566 kg).

Similarly, Van Koevering et al. (1990) and Van Koevering et al. (1991) previously analyzed studies #7, #17, and #19 and concluded that animals fed VM at 27.6 mg/kg of DM increased ADG by 2.4% and F:G by 3.2% compared with MO (27.6 mg/kg of DM). However, because animals in the VM treatment were fatter (more animals classified as USDA-yield grade 4 or above), the authors suggested that the ADG difference would probably be greater if animals were at the same degree of fatness. For 4-wk-old Bohemian spotted bull calves, Skrivanová and Marounek (1993) reported that the inclusion of 80 mg/d of VM increased ADG by 5.1% compared with the control group. Similarly, Rogers et al. (1995) concluded that ADG increased linearly (P < 0.08) with VM ranging from 7.5 to 27.6 mg/kg of DM, without significantly altering DMI and consequently no effect on the F:G ratio. Gorocica and Tedeschi (2017a) concluded that cattle fed VM under European feedlot conditions yielded greater ADG than cattle fed MO (P = 0.03) when compared at the same daily amount. Furthermore, under Mexican feedlot conditions, there is evidence that the combination of VM (200 to 250 mg/d) and MO (400 mg/d) significantly improves ADG (1.544 vs. 1.484 kg/d), F:G (5.88 vs. 6.12), and HCW (307 vs. 302 kg) when compared with supplementing diets with MO alone, respectively (Gorocica and Tedeschi, 2017b).

These results might be influenced by other factors such as the type of diets, methods of grain processing, animal breeds, and feedlot management strategies (Rogers et al., 1995). Boucque et al. (1990) had previously alerted to a possible interaction between VM dosage and diet. Navarrete et al. (2017) tested the effect of VM supplementation on the growth performance of cattle fed varying levels of dietary NE_m (from 2.22 to 2.1 Mcal/kg) and concluded that the positive effect of VM on animal growth might be due to an increased efficiency of energy utilization. For high-forage diets, Mobiglia et al. (2015) reported a 16% increase in ADG (P = 0.074) of Nellore bulls fed with 10% (DM basis) of sugarcane bagasse compared with control when both groups received 25 mg/kg DM VM. The majority of the data used in our analysis, however, were conducted at feedlot conditions in the Midwest of the United States, similar to those used by Navarrete et al. (2017). Furthermore, VM seems to have an inhibitory effect to protozoa (Nagaraja et al., 1995); thus, VM benefits might be amplified when shifts in the ruminal microbial population are observed due to dietary factors.

Liver Abscess Incidence

Only studies #5 and #26 evaluated steers (n = 268) and heifers (n = 270) concurrently. For the control group (no VM), there was no significant dependency between gender and LAI_1–3 (χ²P = 0.266), LAI A− (χ²P = 0.763), or LAI A+ (χ²P = 0.31). Likewise, for the VM group, there was no significant dependency between gender and LAI_1–3 (χ²P = 0.208) or LAI A− (χ²P = 0.759), but for LAI A+, heifers appeared to respond better to VM (χ²P = 0.051) by having less LAI A+ than steers (40.2% vs. 59.8%, respectively). However, because of the small sample size of heifers (3.8%) compared with steers in the database (270 vs. 6,886), we combined steers and heifers data in the subsequent analyses as heifers would be under-represented in the analyses.

Contingency table analyses

Table 2 shows the contingency analysis for LAI_1–3 and LAI A+ vs. with or without VM treatment. Across all treatments for all studies, there were 1,391 animals with LAI_1–3 out of 5,430 animals, and 651 animals that had LAI A+ out of 4,690 animals. There is a significant dependency (χ²P-value < 0.001, fail to accept H₀: they are not independent of each other) and significant asymmetry (McNemar’s test P-value < 0.001) between the incidence of liver abscess and treatment with VM for both LAI_1–3 and LAI A+. The conditional independent test also confirmed a significant (P < 0.001) departure from independence. For the LAI_1–3 group, only 22.5% of the treated animals (all dosages of VM) had liver abscesses compared with 31.7% for the control animals. There are more animals in the control group with liver abscess and fewer animals in the treated group with liver abscesses (or conversely, more animals in the treated group without liver abscesses) than expected. In fact, the odds ratio for LAI_1–3 was 1.59 (P < 0.001; Table 2) indicating that treated animals had about 1.59 [1.40 to 1.81] times greater odds of not having any liver abscess. Similarly, for the LAI A+ group, the χ² test, NcNemar’s test, and conditional independence test indicated a significant (P < 0.001) departure from independence. Only 11.2% of the treated animals (all dosages of VM) had liver abscesses compared with 19.3% for the untreated animals. For the LAI A+ group, the odds ratio of not having liver abscess was about 1.89 [1.59 to 2.24] times greater than those animals in the control (untreated) group (P < 0.001; Table 2). Based on these odds ratios, VM seems to have a greater efficiency for reducing the occurrence of LAI A+ (score 3) than LAI_1–3, though their 95% confidence intervals overlap.

Table 2.

Contingency table for incidences (counts) of liver abscesses for treated and untreated animals with virginiamycin

Liver abscess	Liver abscesses (all scores)			Liver abscess A+ (score 3)
Incidence	Treated	Control	Total	Treated	Control	Total
No	2,781	1,258	4,039	2,781	1,258	4,039
Yes	808	583	1,391	351	300	651
Total	3,589	1,841	5,430	3,132	1,558	4,690
Statistics1	Estimate		P-value	Estimate		P-value
χ2 test	53.04		< 0.001	55.71		< 0.001
McNemar’s test	97.6		< 0.001	510.3		< 0.001
Cond. Indep. test2	5.129		< 0.001	5.694		< 0.001
Odds ratio	1.59 [1.40, 1.81]		< 0.001	1.89 [1.59, 2.24]		< 0.001

¹Statistical tests to assess data independence, H₀ = cell quantities are independent of classificatory variables.

²Conditional independence test.

Table 3 has the contingency table for the incidence or not of liver abscess (LAI_1–3 and LAI A+) vs. different dosage ranges of VM (0, < 15, 15 to 30, > 30 mg/kg DM). For LAI_1–3, the χ² test and the conditional independence test confirmed a highly significant departure from independence (P < 0.001) in which the control group had more animals with liver abscess and the animals treated with >30 mg/kg DM of VM had fewer animals with liver abscess than expected. Similarly, for the LAI A+ group, there was a significant dependence (P < 0.001) of number of animals with or without liver abscesses and different dosage ranges of VM (0, <15, 15 to 30, >30 mg/kg DM) in which the control group had more animals with liver abscess and animals treated with >30 mg/kg DM of VM had fewer animals with liver abscess than expected.

Table 3.

Contingency table for incidences (count) of liver abscesses for untreated (control) and animals treated with virginiamycin at 3 ranges (<15, 15 to 30, >30 mg/kg DM)

Liver abscess	Liver abscesses (all scores)					Liver abscess A+ (score 3)
incidence	Control	<15	15 to 30	>30	Total	Control	<15	15 to 30	>30	Total
No	1258	735	1855	191	4039	1258	735	1855	191	4039
Yes	583	231	571	6	1391	300	106	245	0	651
Total	1841	966	2426	197	5430	1558	841	2100	191	4690
Statistics1	Estimate				P-value	Estimate				P-value
χ2 test	95.03				< 0.001	78.2				< 0.001
Cond. Indep. test2	6.26				< 0.001	5.69				< 0.001

¹Statistical tests to assess data independence, H₀ = cell quantities are independent of classificatory variables.

²Conditional independence test.

The results of these contingency table analyses indicated a significant relationship between receiving and not receiving VM on the incidence of liver abscess (LAI_1–3 and LAI A+). Furthermore, when VM was administered at 30 mg/kg of DM or more, the relationship remained highly significant. The question then becomes at which level of VM we should target for?

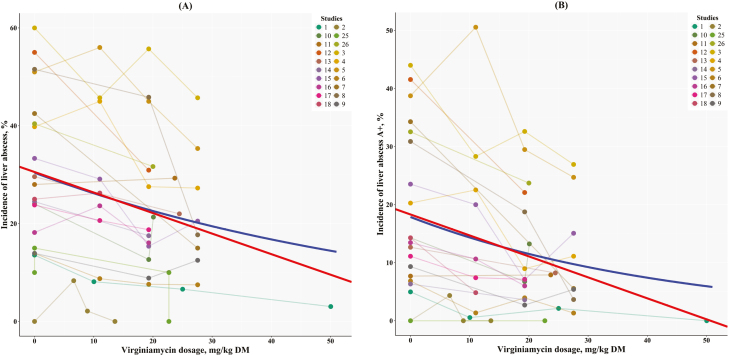
Metaregression analysis

Figure 2 has the metaregression of LAI_1–3 vs. VM dosages. The generalized linear mixed regressions shown in Figure 2A indicated that the percentage of incidence of liver abscesses (i.e., LAI_1–3) was reduced by about 0.42% per increase in VM dosage (P < 0.001), and Figure 2B indicated that the percentage of incidence of liver abscess A+ (i.e., LAI A+) was also reduced by about 0.36% per increase in the VM dosage (P < 0.001). Furthermore, these rates of decrease in the incidence of liver abscesses were not statistically different among themselves (P = 0.34), but because the intercepts were different among them (30.5 vs. 18.3%, respectively; P = 0.021) and there was a significant negative slope, it is expected that the difference in the incidence of liver abscesses (LAI_1–3 and LAI A+) would remain significant as VM dosage increases.

Figure 2.

Relationship between liver abscess incidence using (A) total number of liver abscesses or (B) liver abscess A+ (score 3) vs. virginiamycin dosage (mg/kg DM). The generalized linear mixed regression (red line) for total incidence of liver abscesses was Y = 30.5 (±0.863) – 0.419 (±0.05) × X, r² of 0.542, and SE of 4.45, and for liver abscess A+ (score 3), it was Y = 18.3 (±0.702) – 0.361 (±0.0408) × X, r² of 0.571 and SE of 3.62. The generalized nonlinear mixed regression (blue line) for total incidence of liver abscesses was Y = 30.41 (±3.72) × e^{−0.0149 (±0.0023) × X} with a half-life at 46.6 mg/kg DM, and for liver abscesses A+ (score 3), it was Y = 17.9 (±3.24) × e^{−0.022 (±0.0033) × X} with a half-life at 31.5 mg/kg DM.

Additionally, the generalized nonlinear mixed regression (i.e., exponential decay), also shown in Figure 2 in blue, suggested that the half-time for LAI_1–3 and LAI A+ (i.e., a reduction in LAI_1–3 and LAI A+ by half) would be achieved when VM was fed at 46.6 and 31.5 mg/kg of DM, respectively. Both generalized nonlinear mixed regressions had the least AIC when VC was used for the variance–(co)variance matrix and study effect affected only the intercept. We also estimated that the lower 95% confidence interval of the intercepts for LAI_1–3 and LAI A+ (about 23% and 11.4%, respectively) would occur at 18.7 and 20.3 mg of VM per kilogram of DM. At these concentrations of VM, one would expect a significant difference in the incidence of liver abscess from the control treatment (no VM, i.e., the intercept). Note that the maximum allowable dosage of VM is currently 17.7 mg/kg of DM. Therefore, these analyses confirmed that approximately 18 mg/kg of DM would significantly decrease liver abscesses, but higher dosages might yield additional reduction in the LAI.

Binomial logistic regression

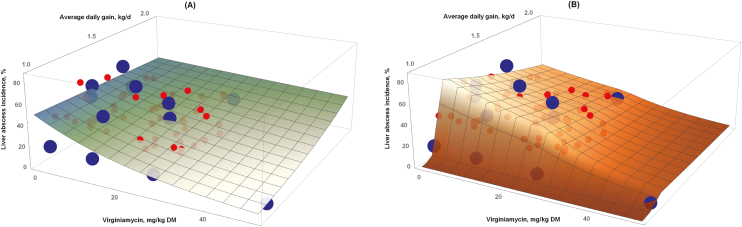
The binomial logistic (logit function) regression for all data points (n = 58; note that we excluded points with probability equal to zero), including multiple observations per VM dosage across studies, to predict LAI_1–3 is shown in equation (2), whereas equation (3) shows the result for a single VM dosage (n = 14; note that we also excluded points with probability equal to zero) combined across studies. The coefficients for the same variable in equations (2) and (3) were not statistically different (P > 0.20), and the ADG coefficients were not statistically different from zero (P < 0.10), resulting in similar predictive patterns. Nonetheless, equation (2) predicts greater estimates of LAI_1–3 than equation (3) for the same ADG and dosage of VM. Figure 3A has the graphical representation of equation (2) across observed ADG and VM dosages,

Figure 3.

The relationship between liver abscess incidence (LAI_1–3, %) vs. ADG (kg/d) and virginiamycin dosage (mg/kg of DM). The large blue dots (≥ 100 animals) and the small red dots (< 100 animals) are observed data points (n = 58). (A) Binomial logistic (logit function) regression, including 58 individual data points: $LA{I}_{1-3}=100\times Exp\left[-0.547-0.07\times dose-0.12\times ADG+0.031\times dose\times ADG\right]$ The coefficient for ADG was not different from zero (P > 0.47). (B) Binomial logistic (logit function) broken-line regression, including 58 individual data points: $LA{I}_{1-3}=100\times Exp(-33.07-0.0214\times \left\{dose<23.9,dose,23.9\right\}-0.06\times \left\{dose<23.9,0,dose-23.9\right\}+28\times \left\{ADG<1.17,ADG,1.17\right\}- 0.762\times \left\{ADG<1.17,0,ADG-1.17\right\})$ All coef- ficients were different from zero (P < 0.05). The breakpoints were 23.9 ± 3.26 mg/kg of DM for virginiamycin and 1.17 ± 0.0111 kg/d for ADG.

$$LA{I}_{1-3}=100\times Exp[-{0.547}^{*}-{0.07}^{***}\times dose-0.12\times ADG+{0.031}^{**}\times dose\times ADG]$$ (2)

$$LA{I}_{1-3}=100\times Exp[-0.963-{0.11}^{***}\times dose-0.14\times ADG+{0.059}^{**}\times dose\times ADG]$$ (3)

where ADG is the average daily gain, kg/d; dose is the VM dosage, mg/kg DM; Exp is the exponential function (i.e., the Napierian number: 2.178); and LAI_1–3 is the LAI of any type (scores 1, 2, or 3), %. The ***, **, and * indicate statistically different from zero at P < 0.001, P < 0.01, and P < 0.05, respectively.

A similar result was obtained for LAI A+. Equations (4) and (5) have the prediction of LAI A+ using a binomial logistic (logit function) regression for all data points (n = 53; note that we excluded points with probability equal to zero) and for the combined LAI A+ for each VM dosage (n = 11; note that we also excluded points with probability equal to zero), respectively. The intercept and the ADG coefficients in equations (4) and (5) were different (P < 0.01), and the dose coefficient did not differ statistically (P = 0.0387). The ADG coefficient in equation (4) was not statistically different from zero (P > 0.05). Figure 4A has the graphical representation of equation (4) across observed ADG and VM dosages,

Figure 4.

The relationship between liver abscess A+ (score 3) incidence (LAI A+, %) vs. ADG (kg/d) and virginiamycin dosage (mg/kg DM). The large blue dots (≥100 animals) and the small red dots (<100 animals) are observed data points, combined across studies (n = 57). (A) Binomial logistic (logit function) regression, including 53 individual data points: $LAI A+=100\times Exp[-1.196-0.0286\times dose-0.128\times ADG$ The coefficient for ADG was not different from zero (P > 0.43). (B) Binomial logistic (logit function) broken-line regression, including 53 individual data points: $LAI A+=100\times Exp(-8.98-0.0191\times \left\{dose<12.34,dose,12.34\right\}-0.0433\times \left\{dose<12.34,0,dose-12.34\right\}+5.89\times \left\{ADG<1.42,ADG,1.42\right\}- 3.286\times \{ADG<1.42,0,ADG-1.42\})$. The first slope for dose was not different from zero (P > 0.05). The breakpoints were 12.34 ± 9.79 mg/kg of DM for virginiamycin and 1.42 ± 0.019 kg/d for ADG.

$$LAIA+=100\times Exp[-{1.19606}^{***}-{0.02861}^{***}\times dose-0.12766\times ADG]$$ (4)

$$LAIA+=100\times Exp[-{3.125098}^{***}-{0.027461}^{***}\times dose+{1.134884}^{***}\times ADG]$$ (5)

where ADG is the average daily gain, kg/d; dose is the VM dosage, mg/kg DM; Exp is the exponential function (i.e., the Napierian number: 2.178); and LAI A+ is the LAI score 3, %. The *** indicates statistically different from zero at P < 0.001.

Equations (2)–(5) confirmed that both LAI_1–3 and LAI A+ decreased as VM dosage increased at an exponential decay pattern, and ADG had a minor influence on the LAI. Although the magnitude may be slightly different, these analyses confirmed the previous results obtained with the metaregression analysis.

Broken-line regression

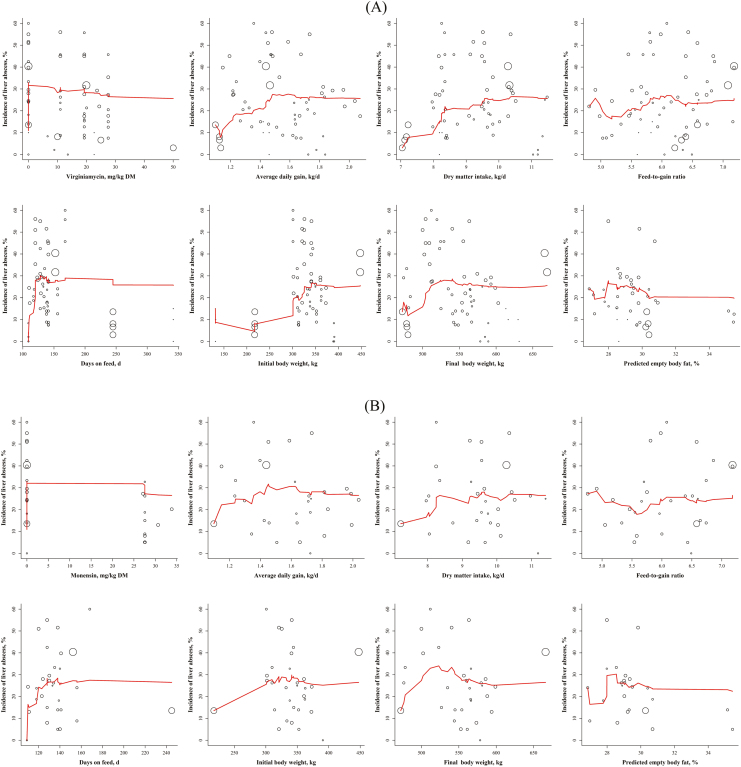
The broken-line analysis for LAI_1–3 indicated 2 statistically significant breakpoints: one at 23.9 ± 3.26 mg/kg of DM of VM and another at 1.17 ± 0.0111 kg/d for ADG (Figure 3B). The breakpoint for VM is approximately 28% greater than the threshold (18.7 mg/kg of DM of VM) obtained in the analysis of the exponential decay from which a difference in LAI_1–3 between treated and control animals would likely to occur. Figure 5 has the graphical representation of LAI_1–3 vs. several variables (inputs and outputs) and their single point-step moving average for VM- or MO-treated animals. For VM-treated animals (Figure 5A), the moving average of ADG, DMI, days on feed (DOF), and initial and final BW tended to increase before reaching an equilibrium (i.e., flat line), whereas the single point-step moving average of dosage and predicted empty body fat tended to decrease before plateauing. For comparative purposes, Figure 5B has the same moving average plots for MO.

Figure 5.

The relationship between liver abscess incidence (LAI_1–3, %) vs. dosage (mg/kg DM), ADG (kg/d), DMI (kg/d), feed-to-gain ratio, days on feed, initial BW (kg), final BW (kg), or predicted empty body fat (% of empty BW) for (A) virginiamycin- and (B) monensin-treated animals. The circles represent the average of each data point (i.e., pen) for the selected studies and their radius size represents the relative proportion of the number of animals in pen compared with the total number of animals used in the plot. The solid red line represents the single step moving average weighed for the number of animals.

Figure 3B also depicts that LAI_1–3 decreased consistently (2.14 %/mg VM /kg of DM) with VM up to 23.9 mg/kg of DM, after which a sharper decline (6 %/mg VM/kg of DM) in LAI_1–3 was observed as VM dosage increased even further. Moreover, Figure 3B shows that LAI_1–3 decreased abruptly for ADG less than 1.17 kg/d. The 95% confidence interval of the VM dosage threshold varied from 17.4 to 30.5 mg/kg of DM, and for ADG it ranged from 1.14 to 1.19 kg/d. Figure 3B indicates that as ADG increased above 1.17 kg/d and VM dosage increased, there was a consistent decrease in LAI_1–3. However, when VM dosage increased above 23.9 mg/kg of DM, there was an even faster reduction in LAI_1–3.

Rogers et al. (1995) used polynomial regression and linear-plateau models to identify 2 thresholds for VM (11 and 19.3 mg/kg DM) of a subset of studies contained in our database. Based on their nonoverlapping confidence interval, they concluded an effective dosage of VM between 16.5 and 19.3 mg/kg DM to reduce LAI_1–3. Their interval overlaps with ours (e.g., 17.4 and 30.5 mg/kg DM), but contrary to their conclusion, our binomial logistic and broken-line regressions suggested a continuous decrease in LAI as VM dosage increases. Our analysis confirmed that animals receiving more than 23.9 mg/kg DM of VM would present significant decreases in the incidence of liver abscesses (Figure 3B). This result is in agreement with the binomial logistic regression results. Although a threshold cannot be established for the ideal dosage of VM, the lower 95% confidence interval of the intercept for LAI (18.7 mg/kg of DM) obtained with the generalized nonlinear mixed regression (Figure 2) is close to the lower 95% confidence interval of the broken-line regression threshold (17.4 mg/kg of DM). Thus, these results confirm that VM dosages above approximately 18 mg/kg of DM (rounded average of 18.7 and 17.4) are likely to yield statistically lower LAI_1–3 compared with the control (no VM). We believe that VM should be fed above 18 mg/kg of DM to observe statistical difference on LAI when compared with control animals, but the maximum reduction in LAI_1–3 might not occur until at least approximately 24 mg of VM/kg of DM is administered. In agreement with our results, Van Koevering et al. (1990) and Van Koevering et al. (1991) previously analyzed studies #7, #17, and #19 and concluded that when animals were fed VM at 19.3 or 27.6 mg/kg of DM, the LAI_1–3 reduced significantly. Rogers et al. (1995) indicated that LAI_1–3 reduces drastically when VM is fed between 11 and 19.3 mg/kg of DM, confirming our results. They, however, in contrast to our findings, indicated no further decrease in LAI when VM was fed above 19.3 mg/kg of DM.

Similarly, Figure 6 has the graphical representation of LAI A+ vs. several variables (inputs and outputs) and their single point-step moving average for VM- or MO-treated animals. For VM-treated animals (Figure 6A), the moving average of ADG, DMI, DOF, and initial and final BW tended to increase before reaching an equilibrium, whereas the moving average of dosage and predicted empty body fat tended to decrease before plateauing. For comparative purposes, Figure 6B has the same moving average plots for MO. In contrast to the similar plots for LAI_1–3 (Figure 5A), VM reduced the incidence of liver abscess A+ at a much lower dosage (12.3 mg/kg of DM) with a 95% confidence interval from 0 to 32.1 mg/kg of DM (Figure 5B). This finding suggests that the incidence of liver abscess A+ can be reduced at smaller concentrations of VM, or in other words, LAI A+ may be reduced more effectively than LAI A– (score 1) or LAI A (score 2). This threshold is, however, about 8 units lower than the breakpoint of 20.3 mg/kg of DM of VM identified by the exponential decay equation as discussed above. The ADG threshold for LAI A+ (1.42 kg/d) was 21% greater than that for LAI_1–3 (1.17 kg/d) and ranged from 1.38 to 1.46 kg/d. However, animals gaining less than 1.42 kg/d had a stiffer decrease in LAI A+ (−589 %/mg VM/kg of DM) than animals gaining more than 1.42 kg/d (328 %/mg VM/kg of DM), as shown in Figure 4B. In contrast, the binomial logistic (logit function) regression (Figure 4A) suggested a steady decline in LAI A+ with VM dosage and little effect of ADG. The ADG threshold in Figure 4B might be an artifact of the large sample size of animals gaining around 1.4 kg/d, but it is clear that LAI A+ decreased consistently (1.91 %/mg VM/kg DM) with VM up to 12.34 mg/kg DM, after which a sharper decline (4.33 %/mg VM/kg DM) in LAI A+ was observed as VM dosage increased. Similar to the LAI_1–3 analyses, LAI A+ decreased continuously as VM dosage increased (Figure 6A). Because the breakpoint for LAI+ is about half of that obtained for LAI_1–3 (12.3 vs. 23.9 mg/kg of DM, respectively) and the lower 95% confidence interval of the breakpoint for LAI+ is zero, we believe that there is enough evidence to suggest that the incidence of liver abscess A+ is reduced earlier than LAI₁, LAI₂, and LAI₃ together when VM is fed.

Figure 6.

The relationship between liver abscess incidence A+ (LAI A+, %) vs. dosage (mg/kg DM), ADG (kg/d), DMI (kg/d), feed-to-gain ratio, days on feed, initial BW (kg), final BW (kg), or predicted empty body fat (% of empty BW) for (A) virginiamycin- and (B) monensin-treated animals. The circles represent the average of each data point (i.e., pen) for the selected studies and their radius size represents the relative proportion of the number of animals in pen compared with the total number of animals used in the plot. The solid red line represents the single step moving average weighed for the number of animals.

Residual-based shading analyses

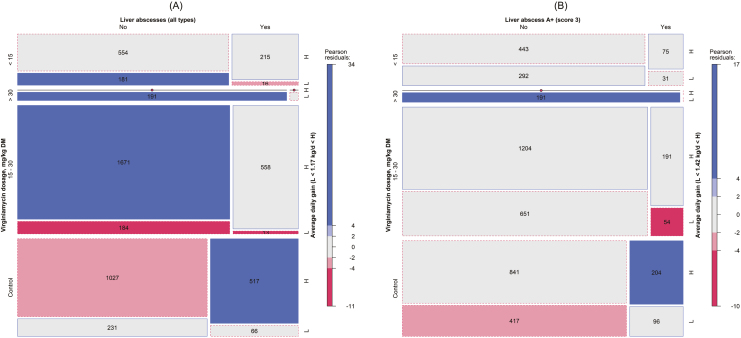
Given the significant relationship between LAI_1–3 and LAI A+, VM dosages, and ADG, a 3-way contingency table analysis was conducted and mosaic displays were used to show their relationships visually (Figure 7). Four classes of VM dosages were used: 0 (control), <15, 15 to 30, and >30 mg/kg DM. Based on the broken-line regression, for LAI_1–3, a cutoff of 1.17 kg/d was assumed for ADG (L: < 1.17 and H: ≥ 1.17 kg/d), and for LAI A+, a cutoff of 1.42 kg/d was assumed for ADG (L: < 1.42 and H: ≥ 1.42 kg/d) for consistency.

Figure 7.

Mosaic displays of contingency tables for (A) liver abscesses (all types, LAI_1–3) or (B) liver abscess A+ (LAI A+) vs. virginiamycin dosage ranges (control, <15, 15 to 30, and >30 mg/kg DM) vs. ADG ranges (L < 1.17 kg/d < H and L < 1.42 kg/d < H for (A) and (B), respectively). The numbers within a cell are the observed counts, but for cell counts with less than 10 the value is not shown. The area of the cell (square or rectangle) represents the quantities (counts), the cell’s width represents the marginal probability within the row (virginiamycin dosage), the cell’s height represents the marginal probability within the column (liver abscess), and the cell’s color represents the standardized Person residual from independence (solid outlines are positive residual and dashed outlines are negative residuals).

For LAI_1–3, the conditional independence test confirmed a significant departure from independence among LAI_1–3, VM dosages, and ADG (6.26; P < 0.001; Table 3). Figure 7A has the mosaic display for the total incidence of liver abscess (all scores). When compared with the expected counts (i.e., Person residual; shown in Figure 8A), there was a greater number of animals in the control high-gain (gained more than 1.42 kg/d) group that had LAI (517; Figure 7A) than expected (488; Figure 8A). Furthermore, when compared with the expected counts (Figure 8A), there were more animals in the high-gain 15 to 30 mg/kg DM VM class without liver abscess (1,671; Figure 7A) than expected (1,552; Figure 8A). Figure 7A graphically confirms previous analysis results that more liver abscess-free animals were located in the VM treatment (left side and blue color).

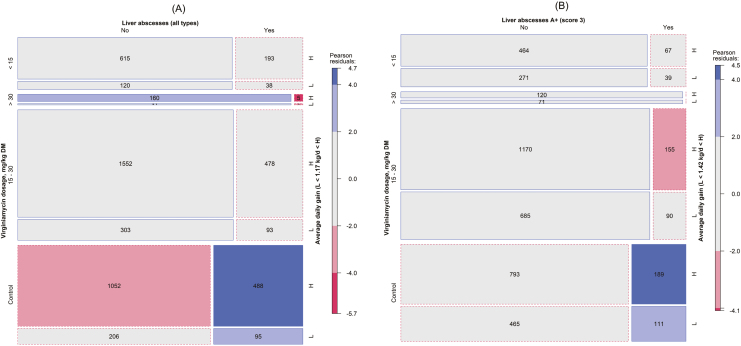
Figure 8.

Mosaic displays of contingency tables for (A) expected liver abscesses (all types, LAI_1–3) or (B) expected liver abscess A+ (LAI A+) vs. virginiamycin dosage ranges (control, <15, 15 to 30, and >30 mg/kg DM) vs. ADG ranges (L < 1.17 kg/d < H and L < 1.42 kg/d < H for (A) and (B), respectively). The numbers within a cell are the expected counts, but for cell counts with less than 10 the value is not shown. The area of the cell (square or rectangle) represents the quantities (counts), the cell’s width represents the marginal probability within the row (virginiamycin dosage), the cell’s height represents the marginal probability within the column (liver abscess), and the cell’s color represents the standardized Person residual from independence (solid outlines are positive residual and dashed outlines are negative residuals).

For LAI A+, the conditional independence test confirmed a significant departure from independence among LAI A+, VM dosages, and ADG (5.69; P < 0.001; Table 3). Figure 7B has the mosaic display for the incidence of liver abscess A+. Similar to the LAI, when compared with the expected counts (i.e., Person residual; shown in Figure 8B), there was a higher number of animals in the control high-gain (gained more than 1.42 kg/d) group that had LAI A+ (204; Figure 7B) than expected (189; Figure 8B). Furthermore, when compared with the expected counts, there were fewer animals with liver abscess in the high-gain 15 to 30 (54) and <15 (31) mg/kg of DM VM classes than expected (90 and 39, respectively). When comparing Figure 7A and Figure 7B, it is clear that the control group without LAI A+ (Figure 7B) was within the expected values compared with the LAI_1–3 (Figure 7A) that was less than expected for animals gaining more than 1.17 kg/d.

Streptococcus bovis and Lactobacillus spp. are the best known and studied Gram-positive microbes that produce lactate in the rumen (Hungate, 1966; Russell and Hino, 1985) that contribute to the development of acidosis in the rumen. When high-grain diets are introduced to feedlot animals, and adequate feeding strategies are not followed, lactate production by lactic acid-producing bacteria outstrips the ability of lactate-fermenting bacteria to utilize it. Populations of lactating-utilizing bacteria (e.g., Megasphaera elsdenii, Selenomonas ruminantium, Propionibacterium spp.) increase, but their growth rates are often not fast enough to keep up with the rapidly growing (and fermenting) of lactate producers in the rumen microbiome. As a result, lactic acid begins to accumultate in the rumen from the rapid fermentation of starch and soluble carbohydrates, ultimately leading to the development of systematic acidosis (Owens et al., 1998). In these situations, feed additives such as VM can decrease the accumulation of lactate in the rumen by decreasing the proportion of the population made up of lactic acid-producing Gram-positive microbes (Rowe et al., 1991). Positive effects of VM have been reported in feedlot animals receiving high-grain diets (Coe et al., 1999) as well as grazing dairy cattle receiving concentrate supplements (Clayton et al., 1999) arguably due to the reduction in ruminal lactate accumulation with a consequent reduction in liver abscesses. Fortunately, our results suggest that VM might be more effective for LAI A+ than LAI A– and LAI A.

Furthermore, Corpet (2000) concluded that growth-enhancing antibiotics might promote maximum efficiency in farms because of their ability to control pathologies and consequently increase nutrient supply to the host animal, especially in those farms with poor hygiene. Based on our analyses, regardless the animal ADG, the incidence of liver abscess (i.e., LAI_1–3) and LAI A+ was reduced continuously as the administration of VM increases. Given the threshold analysis, it is apparent that the reduction in LAI A+ occurs earlier than the reduction in LAI. Thus, animals may benefit the most when VM is administered above 12 mg/kg of DM. For feedlot animals, the recommendation is to provide between 12 and 24 mg/kg of DM of VM for excellent management practices. Furthermore, VM should be fed above 24 mg/kg of DM or higher to maximize the reduction of LAI_1–3 or when VM is administered under poor management conditions.

Although the LAI has been previously correlated with Fusobacteria (Nagaraja and Chengappa, 1998) and Actinobacteria (Narayanan et al., 1998), Weinroth et al. (2017) indicated that additional phyla (Bacteroidetes, Proteobacteria, and Firmicutes) have also been associated with liver abscess through the sequencing of the V4 region of the 16S rRNA gene. Also, different animal breeds may have different and specific bacterial species that are more prominent in causing liver abscesses (Amachawadi et al., 2017). In summary, it seems that the incidence of liver abscess in feedlot animals is the result of a multitude of factors (dietary, animal breed, bacterial species, and management); thus, a combination of different managerial and feeding strategies might be necessary to prevent liver abscess.

In conclusion, we used different statistical analyses (metaregression, binomial logistic regression, broken-line regression, contingency table, and residual-based shading analysis) to evaluate the effectiveness of VM on the incidence of liver abscess (LAI_1–3 and LAI A+) and animal growth of different studies conducted with diverse breeds of animals and feedlot management criteria. The statistical analyses resoundingly confirmed that VM is effective in reducing the total incidence of total liver abscesses and A+ scoring liver abscesses. The broken-line analyses indicated that VM between 12 and 24 mg/kg DM is the most effective in reducing liver abscesses. When administered above 18 mg/kg of DM, there is an even higher probability of observing statistical difference on LAI_1–3 compared with control animals, but the maximum reduction in LAI might not occur below 24 mg of VM/kg of DM.