Cerebral Metabolic Rate of Oxygen (CMRO2) Mapping by Combining Quantitative Susceptibility Mapping (QSM) and Quantitative Blood Oxygenation Level Dependent Imaging (qBOLD)

Abstract

Purpose

To map the cerebral metabolic rate of oxygen (CMRO2) by estimating the oxygen extraction fraction (OEF) from gradient echo imaging (GRE) using phase and magnitude of the GRE data.

Theory and Methods

3D multi-echo gradient echo imaging and perfusion imaging with arterial spin labeling were performed in 11 healthy subjects. CMRO2 and OEF maps were reconstructed by joint quantitative susceptibility mapping (QSM) to process GRE phases and quantitative Blood Oxygen Level Dependent (qBOLD) modeling to process GRE magnitudes. Comparisons with QSM and qBOLD alone were performed using ROI analysis, paired t-tests, and Bland-Altman plot.

Results

The average CMRO2 value in cortical gray matter across subjects were 140.4 ± 14.9, 134.1 ± 12.5, 184.6 ± 17.9 µmol/100g/min, with corresponding OEFs of 30.9 ± 3.4%, 30.0 ± 1.8%, 40.9 ± 2.4% for methods based on QSM, qBOLD, and QSM+qBOLD, respectively. QSM+qBOLD provided the highest CMRO2 contrast between gray and white matter, more uniform OEF than QSM, and less noisy OEF than qBOLD.

Conclusion

Quantitative CMRO2 mapping that fits the entire complex GRE data is feasible by combining QSM analysis of phase and qBOLD analysis of magnitude.

INTRODUCTION

Cerebral metabolic rate of oxygen (CMRO2) and oxygen extraction fraction (OEF) maps are valuable for evaluating neurologic disorders such as ischemic stroke (1,2). Gradient echo (GRE) MR signal is highly sensitive to the strongly paramagnetic deoxyhemoglobin converted from weakly diamagnetic oxyhemoglobin. Several techniques have been proposed to estimate these maps based on quantitative modeling of either MRI magnitude or phase data. Magnitude modeling methods include quantitative imaging of extraction of oxygen and tissue consumption (QUIXOTIC) (3), calibrated fMRI (4–7) and quantitative BOLD (qBOLD) (8,9). Phase modeling methods have been used for whole brain CMRO2 measurements (10,11). Building on this, quantitative susceptibility mapping (QSM) (12,13) enables generating CMRO2 maps (14,15). The QSM-based CMRO2 methods separate voxel-wise susceptibility into non-blood tissue susceptibility (χ_nb) and blood susceptibility mainly driven by deoxyhemoglobin in the venous blood. The latter is then used to compute tissue oxygen consumption.

There are several challenges to the current CMRO2 mapping methods. qBOLD approximates χ_nb from fully oxygenated blood (9,16), but it ignores tissue iron stored in ferritin or myelin that contributes to the rich χ_nb contrast in the brain. QSM-based methods assume a fixed and empirical linear relationship between the venous blood volume fraction (v) and cerebral blood flow (CBF) to obtain v (17), but this relationship may vary with tissues and diseases. While qBOLD estimates v directly from the data, it assumes that χ_nb is constant. On the contrary, QSM-based methods assume v from CBF, whereas χ_nb is estimated from the data. Since both methods use the same underlying gradient echo data, we propose to combine QSM and qBOLD (QSM+qBOLD) to map the OEF and CMRO2 overcoming these assumptions.

THEORY

CMRO2 (µmol/100g/min) and OEF (%) can be expressed as

$$\mathit{\text{CMRO}}2=\mathit{\text{CBF}}·\mathit{\text{OEF}}·{[H]}_a$$ [1]

$$\mathit{\text{OEF}}=1-\frac{Y}{Y_a}$$ [2]

where CBF is the cerebral blood flow (ml/100g/min), [H]_a is the oxygenated heme molar concentration in the arteriole (7.377 µmol/ml) estimated from [H]_a = [H] · Y_a, where [H] = 7.53 µmol/ml is the heme molar concentration in tissue blood assuming a hematocrit of Hct = 0.357 (18). Y_a and Y are the arterial (assumed to be 0.98) and venous oxygenation. Hct, Y, and Y_a are dimensionless fractions.

QSM-based CMRO2 methods require estimating two unknowns per voxel (14,15,18): venous oxygenation Y and non-blood susceptibility χ_nb. The venous blood volume fraction (v) is assumed to be known by an empirically derived linear relationship between cerebral blood flow (CBF) and v obtained using positron emission tomography (PET) in healthy subjects (17). However, since this assumption may break down in disease such as stroke (19), v should be treated as a parameter estimated from data. The qBOLD-based CMRO2 method (20) expresses the magnitude of the GRE signal of each voxel as a function of four unknowns: signal intensity at TE=0 (S⁰), transverse relaxation rate (R₂), v, and Y (8,16,20). qBOLD further treats χ_nb, which varies spatially due to iron and myelin content, as the same as that of fully oxygenated blood. In the proposed QSM+qBOLD method, both v and χ_nb are treated as unknowns, and the QSM and qBOLD signal equations are combined according to maximum likelihood (ML) under Gaussian noise approximation (21). The ML estimation finds the parameter set (Y, v, χ_nb, S⁰, R₂) which maximizes the probability of observing the voxel-wise susceptibility QSM and the magnitude signals S(TM) assuming respective signal models F_QSM(Y, v, χ_nb) and F_qBOLD(Y, v, χ_nb, S⁰, R₂, TE). These signal models build upon prior QSM (18) and qBOLD models (20) but are modified to properly model v and χ_nb, as detailed below in Eqs. 4 and 7. Assuming Gaussian noise, this is equivalent to minimizing the cost function:

$$\begin{gathered} Y^{\ast },v^{\ast },{\chi }_{\mathit{\text{nb}}}^{\ast },S^{0\ast },R_2^{\ast } \\ =\underset{Y,v,{\chi }_{\mathit{\text{nb}}},S^0,R_2}{\text{argmin}}\{{\sum }_{\mathit{\text{TE}}}{\Vert |S(\mathit{\text{TE}})|-F_{\mathit{\text{qBOLD}}}(Y,v,{\chi }_{\mathit{\text{nb}}},S^0,R_2,\mathit{\text{TE}})\Vert }_2^2+ \\ w{\Vert \mathit{\text{QSM}}-F_{\mathit{\text{QSM}}}(Y,v,{\chi }_{\mathit{\text{nb}}})\Vert }_2^2\} \end{gathered}$$ [3]

where ‖·‖₂ is the L2 norm and w the weight on the QSM model of phase data. The first term in Eq. 3 is the qBOLD model of magnitude data (20):

$$F_{\mathit{\text{qBOLD}}}(Y,v,{\chi }_{\mathit{\text{nb}}},S^0,R_2,\mathit{\text{TE}})=S^0·e^{-R_2·\mathit{\text{TE}}}·F_{\mathit{\text{BOLD}}}(v,Y,{\chi }_{\mathit{\text{nb}}},\mathit{\text{TE}})·G(\mathit{\text{TE}})$$ [4]

where G is the macroscopic field inhomogeneity contributing to the GRE signal (see Appendix) and F_BOLD is the GRE signal decay due to deoxygenated blood in vessel network: $F_{\mathit{\text{BOLD}}}(v,Y,{\chi }_{\mathit{\text{nb}}},\mathit{\text{TE}})=1-\frac{v}{1-v}·f_s(\delta \omega ·\mathit{\text{TE}})+\frac{1}{1-v}·f_s(v·\delta \omega ·\mathit{\text{TE}})$. The function f_s is the signal decay by the blood vessel network (20,22), whose asymptotic behavior is $f_s(\delta \omega ·\mathit{\text{TE}})\approx \frac{3}{10}{(\delta \omega ·\mathit{\text{TE}})}^2$ for TE ≪ 1/δω, and f_s(δω · TE) ≈ δω · TE for $\mathit{\text{TE}}\gg \frac{1}{\delta \omega }$, where δω is the characteristic frequency due to the susceptibility difference between deoxygenated blood and the surrounding tissue:

$$\delta \omega (Y,{\chi }_{\mathit{\text{nb}}})=\frac{1}{3}·\gamma ·B_0·[\text{Hct}·\mathrm{\Delta }{\mathrm{\chi }}_0·(1-Y)+{\chi }_{\mathit{\text{ba}}}-{\chi }_{\mathit{\text{nb}}}]$$ [5]

where γ is the gyromagnetic ratio (267.513 MHz/T), B₀ is the main magnetic field (3T in our study), Hct is hematocrit (0.357) (18), Δχ₀ is the susceptibility difference between fully oxygenated and fully deoxygenated red blood cell (4π × 0.27ppm) (23), χ_ba is the susceptibility of fully oxygenated blood, −108.3 ppb estimated with using Hct 0.357 (15). Note that the qBOLD assumption of neglecting susceptibility differences between non-blood tissue and fully oxygenated blood (χ_ba = χ_nb) (8,16,20,24) is not made here.

The second term in Eq. 3 contains the signal equation for the susceptibility of a voxel, F_QSM, which is the sum of three terms: the non-blood tissue susceptibility, the plasma susceptibility and the hemoglobin susceptibility (15,18):

$$F_{\mathit{\text{QSM}}}=(1-\mathit{\text{CBV}})·{\chi }_{\mathit{\text{nb}}}+\mathit{\text{CBV}}·(1-{\psi }_{\mathit{\text{Hb}}})·{\chi }_p+\mathit{\text{CBV}}·{\psi }_{\mathit{\text{Hb}}}·[{\chi }_{\mathit{\text{oHb}}}+\mathrm{\Delta }{\chi }_{\mathit{\text{Hb}}}·\frac{v·{[\mathit{\text{dH}}]}_v+(\mathit{\text{CBV}}-v)·{[\mathit{\text{dH}}]}_a}{\mathit{\text{CBV}}·[H]}]$$ [6]

where CBV is total blood volume (dimensionless fraction), ψ_Hb the hemoglobin volume fraction (dimensionless) which was set to 0.0909 for tissue based on Hct 0.357 (18,25–27), χ_p the blood plasma susceptibility, set to −37.7 ppb (28), χ_oHb the oxyhemoglobin susceptibility (−813 ppb) (18,26,29), [dH]_v and [dH]_a the concentration (µmol/ml) of deoxyhemoglobin in venules and arterioles, respectively. [dH]_v and [dH]_a will be expressed in terms of Y and Y_a below. Finally, Δχ_Hb is the susceptibility difference between deoxy- and oxy-hemoglobin (12522 ppb) (14,28).

Eq. 6 is then expressed in terms of 1) the ratio between the venous and total blood volume α = v/CBV, assumed to be constant (0.77) (30), 2) the fully oxygenated blood susceptibility, χ_ba = ψ_Hb · χ_oHb + (1 − ψ_Hb) · χ_p (15), 3) the arterial oxygenation $Y_a=\frac{[H]-{[\mathit{\text{dH}}]}_a}{[H]}$, and 4) the venous oxygenation, $Y=\frac{[H]-{[\mathit{\text{dH}}]}_v}{[H]}$. This results in:

$$F_{\mathit{\text{QSM}}}(Y,v,{\chi }_{\mathit{\text{nb}}})=[\frac{{\chi }_{\mathit{\text{ba}}}}{\alpha }+{\psi }_{\mathit{\text{Hb}}}·\mathrm{\Delta }{\chi }_{\mathit{\text{Hb}}}·(-Y+\frac{1-(1-\alpha )·Y_a}{\alpha })]·v+(1-\frac{v}{\alpha })·{\chi }_{\mathit{\text{nb}}}$$ [7]

where the two terms represent the contribution of blood and non-blood tissue to the total susceptibility, respectively. Note that v, which was estimated from CBF in QSM-based CMRO2 mapping methods (14,15,18), is now an unknown to be determined by data.

This QSM+qBOLD model is compared with two previous methods: 1) a QSM method with minimum local variance (MLV) (18) (“QSM” hereafter), and 2) qBOLD that models the complex multi-echo gradient echo data as (20) (“qBOLD” hereafter):

$$S(\mathit{\text{TE}})=S^0·e^{-R_2·\mathit{\text{TE}}}·e^{i\mathrm{\Delta }f·\mathit{\text{TE}}}·F_{\mathit{\text{BOLD}}}(v,Y,{\chi }_{\mathit{\text{ba}}},\mathit{\text{TE}})·G(\mathit{\text{TE}})$$ [8]

METHODS

Data Acquisition

This study was approved by the local Institutional Review Board. Healthy volunteers were recruited (n=11; 10 males, 1 female, mean age 34 ± 12 years) for brain MRI on a 3T scanner (HDxt, GE Healthcare) using an 8-channel brain receiver coil. After obtaining consent, all subjects were instructed to avoid caffeine or alcohol intake 24 hours prior to the MRI.

MRI was performed in the resting state (15) using a 3D fast spin echo (FSE) arterial spin labeling (ASL) sequence (31–33), a 3D multi-echo spoiled gradient echo (GRE) sequence (13,34,35), and an inversion prepared T1w SPGR sequence (BRAVO) (36). The 3D FSE ASL sequence parameters were: 20 cm FOV, 1.56 mm in-plane resolution, 3.5 mm slice thickness, 1500 ms labeling period, 1525 ms post-label delay, 976.6 Hz/pixel bandwidth, spiral sampling of 8 interleaves with 512 readout points per leaf, 35 axial slices, 10.1 ms TE, 4533 ms TR, and 3 signal averages. The 3D GRE sequence parameters were: 0.78 mm in-plane resolution, 1.2 mm slice thickness, volume coverage identical to the 3D FSE ASL sequence, 7 equally spaced echoes, 2.3 ms for the first TE, 3.9 ms echo spacing, 30.5 ms TR, 488.3 Hz/pixel band width, and 15^o flip angle. The pulse sequence was flow-compensated in all three directions (34). The inversion prepared T1w SPGR sequence parameters were: 0.78 mm in-plane resolution, 1.2 mm slice thickness, volume coverage identical to the 3D FSE ASL sequence, 2.92 ms TE, 7.69 ms TR, 450 ms prep time, 195.2 Hz/pixel bandwidth, and 15^o flip angle.

Image Processing

QSM reconstruction was performed as follows: first, an adaptive quadratic-fit of the GRE phase was used to estimate the total field (34). Second, the Projection onto dipole fields (PDF) method was used to obtain the local field (35). Finally, the Morphology Enabled Dipole Inversion (MEDI) algorithm was used to compute susceptibility (12,13,37). The susceptibility values were referenced to the susceptibility of cerebrospinal fluid (CSF) averaged over a manually drawn ROI on the first echo of the GRE acquisition. CBF maps (ml/100g/min) were generated from the ASL data using the FuncTool software package (GE Healthcare, Waukesha, WI, USA). All images were co-registered and interpolated to the resolution of the QSM maps using the FSL FLIRT algorithm (38,39).

Optimization

To improve convergence behavior during nonlinear fitting, the five unknowns v, Y, χ_nb, S⁰, R₂ were scaled to have roughly the same order of magnitude as the initial guess: $x\mapsto \frac{x}{|x_0|}$, where x is the unknown in the original scale and x₀ is the corresponding initial guess. Initial guesses were obtained as follows: Y₀ was estimated from the straight sinus (SS) as the global constraint in previous QSM-based CMRO2 studies (15,18), Y₀ = Y_a · (1 − OEF_ss/Hct_ratio where Hct_ratio is the hematocrit ratio (0.759) between large vessels and brain tissue (25) and OEF_ss = 1− Y_ss/Y_a (Y_ss was estimated from QSM in SS with setting ψ_Hb = 0.1197 for large veins (18,26,27), v = 1 and χ_nb = 0 in Eq. 7). v₀ was set using the linear relationship between CBF and v (14,15,18). χ_nb,0 was set as the susceptibility of fullyoxygenated blood as in the qBOLD methods (8,16,20). $S_0^0$ and R_2,0 were obtained by performing a mono-exponential fit against Eq. 4 after fixing the values of G (40) and F_BOLD with the initial values Y₀, v₀, and χ_nb,0. The function G was calculated using the voxel spread function (VSF) method (41). For some voxels the initials guess for Y was not appropriate leading to an increase in signal as a function of TE after dividing out the F_BOLD contribution. This then led to a negative R_2,0. To avoid this situation, Y was gradually increased to insure a positive R_2,0.

To speed up the F_BOLD calculation, we used a Taylor expansion of the hypergeometric function (₁F₂) up to the 60^th order (20). The lower and upper bounds were set to 0.5 and 2 for each scaled unknown, except for Y, which used the 0.1 and 0.9 bounds before scaling. At the start of each optimization, both the QSM and qBOLD terms in Eq. 3 were normalized by their respective values evaluated with the initial guess to compensate for the arbitrary scale of input MRI data. The tuning parameter w was selected using the L-curve method (42). Corners of the L-curves for two randomly chosen subjects were both located at w = 100 (Fig. 1). The limited-memory Broyden-Fletcher-Goldfarb-Shanno-Bound algorithm was used for the constrained optimization (43,44). The optimization was stopped when the relative residual ${\mathrm{r}}_{\mathrm{i}}=\frac{E_i-E_{i-1}}{E_i}$, with E_i as the energy of the ith iteration, was smaller than 0.005.

Figure 1.

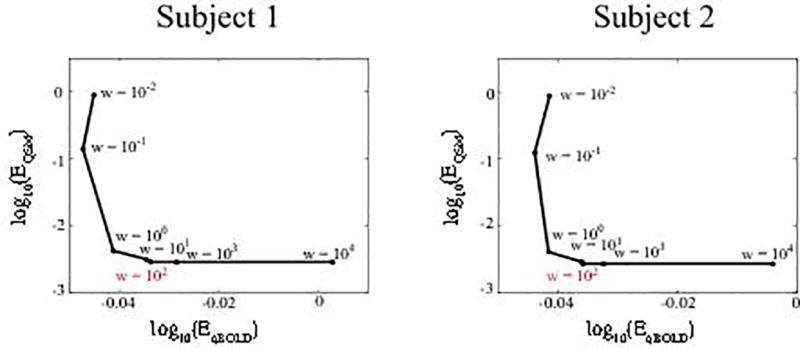
L-curves in two randomly selected subjects to determine tuning parameter w. The L-curve corners were located at w=100 in both subjects. E_qBOLD and E_QSM indicate the energy terms in Eq. 3.

For “QSM”, the optimization followed the previous QSM-based method using the MLV method and global CMRO2 constraint (18). For “qBOLD”, the optimization was performed voxel-wise, following (20). The parameter scaling, initial guess, and boundary conditions were set in the same manner as for QSM+qBOLD. In addition, the initial frequency shift Δf₀ was set to the total field value as obtained in the QSM process (13).

Statistical Analysis

ROI analyses (mean and standard deviation), paired t-tests (at 0.01 significance level), and Bland-Altman analyses were performed to compare CMRO2 and OEF values between the QSM-based (18), qBOLD (20), and QSM+qBOLD methods. For the ROIs, the bilateral anterior (ACA), middle (MCA) and posterior (PCA) cerebral artery vascular territories (VT) in the cortical gray matter (CGM) and white matter (WM) masks were constructed based on T1-weighted images by a neuroradiologist with 10 years of experience.

RESULTS

The CMRO2 in CGM were 140.4 ± 14.9, 134.1 ± 12.5, 184.6 ± 17.9 µmol/100g/min (N=11) for the QSM, qBOLD, and QSM+qBOLD models, respectively. These corresponded to OEFs of 30.9 ± 3.4%, 30.0 ± 1.8%, 40.9 ± 2.2%, respectively (Supporting Table S1).

In Fig. 2, compared to QSM and qBOLD, QSM+qBOLD showed higher CMRO2 contrast between CGM and WM: 21.9 ± 9.4 (p<0.01), 36.0 ± 6.4 (p<0.01), 54.6 ± 10.3 µmol/100g/min (N=11) for the QSM, qBOLD, and QSM+qBOLD models, respectively. QSM showed a smoother CMRO2 map than QSM+qBOLD, except for a sharp transition at the GM/WM boundary.

Figure 2.

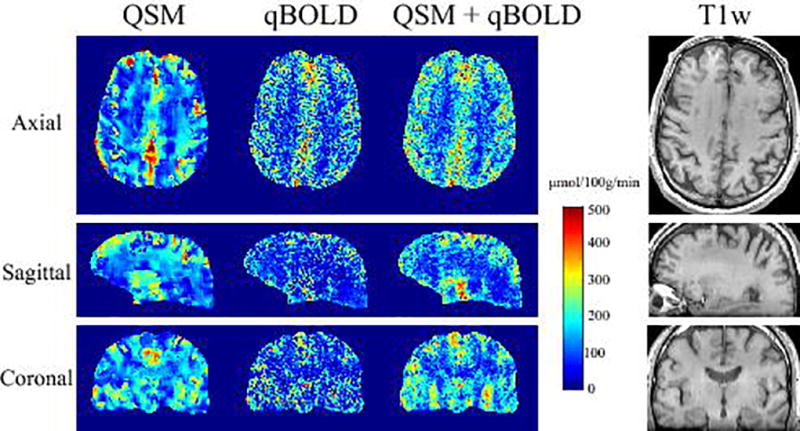
CMRO2 map in axial, sagittal, and coronal sections from a subject reconstructed using QSM, qBOLD, and QSM+qBOLD methods. The corresponding T1-weighted anatomical images are shown on the right. QSM+qBOLD shows higher GM/WM contrast than QSM or qBOLD.

In Fig. 3, QSM+qBOLD showed higher OEF than the two individual methods; the OEF values for whole brain were 34.5 ± 3.1 % (p<0.01), 29.8 ± 2.1% (p<0.01), and 39.3 ± 2.2 % (N=11) for QSM, qBOLD, and QSM+qBOLD, respectively. QSM+qBOLD showed a relatively uniform OEF map as compared to QSM, and a less noisy OEF map than qBOLD. The OEF standard deviations in CGM was lower for QSM+qBOLD than for each individual methods: 16.3 ± 0.9 % (p<0.01), 19.4 ± 1.5 % (p<0.01), and 12.3 ± 1.2 % (N=11) for QSM, qBOLD, and QSM+qBOLD, respectively. The venous blood volume v was slightly higher for QSM+qBOLD as compared to QSM and qBOLD: in CGM, the values were 4.3 ± 0.4 % (p<0.01), 4.1 ± 0.4% (p<0.01), and 4.5 ± 0.4%, and in WM, 3.5 ± 0.3 % (p=0.011) and 3.2 ± 0.3% (p<0.01), and 3.5 ± 0.3% for QSM, qBOLD and QSM+qBOLD, respectively. χ_nb from QSM and QSM+qBOLD showed similar contrast at the CGM/WM boundary, it was higher in CGM than in nearby WM. Average χ_nb values were similar between QSM and QSM+qBOLD as compared to qBOLD (−108.3 ppb assumed for the whole brain): −12.3 ± 3.7 ppb (p<0.01) and −19.8 ± 3.5 ppb in CGM, and −15.3 ± 3.9 ppb (p<0.01) and −18.7 ± 3.5 ppb in WM (N=11) for QSM and QSM+qBOLD, respectively. The v map of the QSM model and the χ_nb of the qBOLD model were not obtained through optimization, but given by a priori assumptions.

Figure 3.

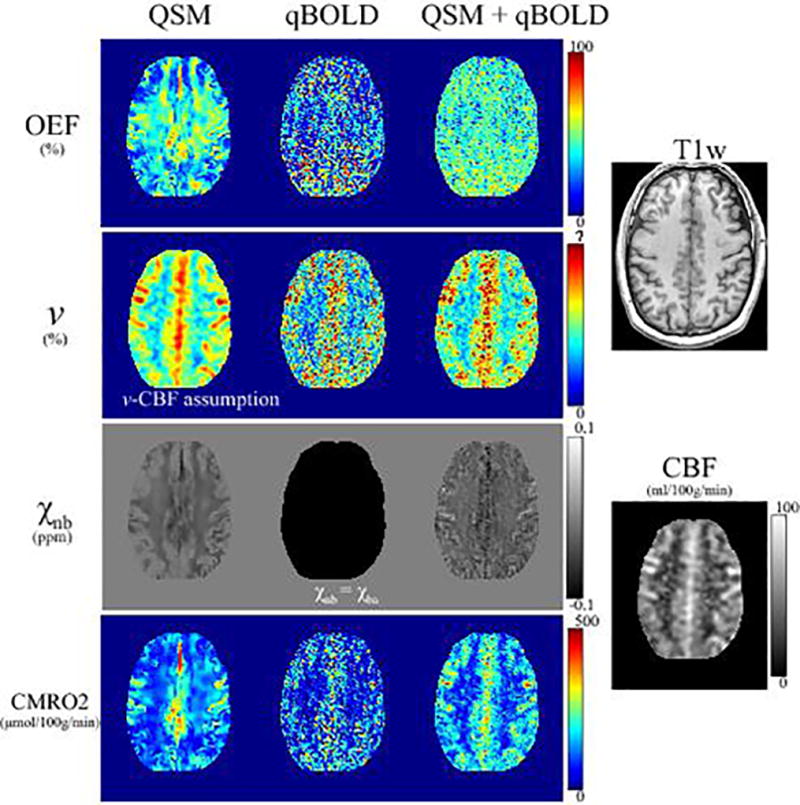
OEF, venous volume (v), non-blood tissue susceptibility (χ_nb), and CMRO2 maps in a second subject reconstructed using QSM, qBOLD, and QSM+qBOLD models. The OEF obtained using QSM+qBOLD is more uniform than that of QSM, and is greater than that of qBOLD.

In Fig. 4, QSM+qBOLD showed higher CMRO2 and OEF values than both QSM and qBOLD in all ACA, MCA, PCA, and WM ROIs (p<0.01). All three methods showed lower CMRO2 in WM than in ACA, MCA, and PCA (p<0.01).

Figure 4.

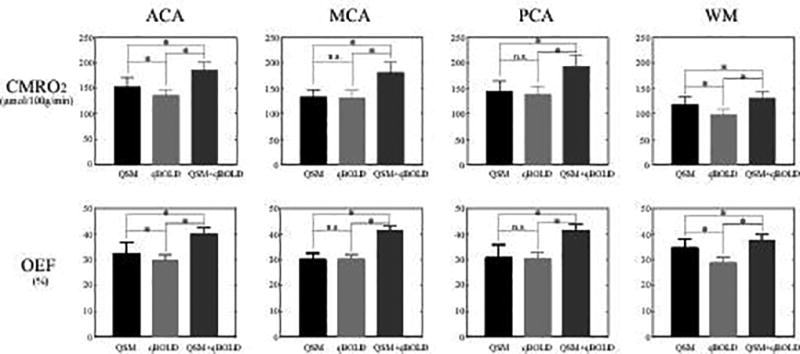
ROI comparison of CMRO2 and OEF in ACA, MCA, PCA, and WM among QSM (black), qBOLD (gray), and QSM+qBOLD (dark gray). In all ROIs, QSM+qBOLD provides higher CMRO2 and OEF values than QSM or qBOLD (p<0.01). * p < 0.01 (paired t-test). “n.s.” indicates that the difference is not significant (p>0.1).

In the Bland-Altman plots (Fig. 5), the mean differences were 43.5 µmol/100g/min (QSM vs QSM+qBOLD) and 51.2 µmol/100g/min (qBOLD vs QSM+qBOLD) for CMRO2 (p<0.01), and 9.8 % (QSM vs QSM+qBOLD) and 10.9 % (qBOLD vs QSM+qBOLD) for OEF (p<0.01).

Figure 5.

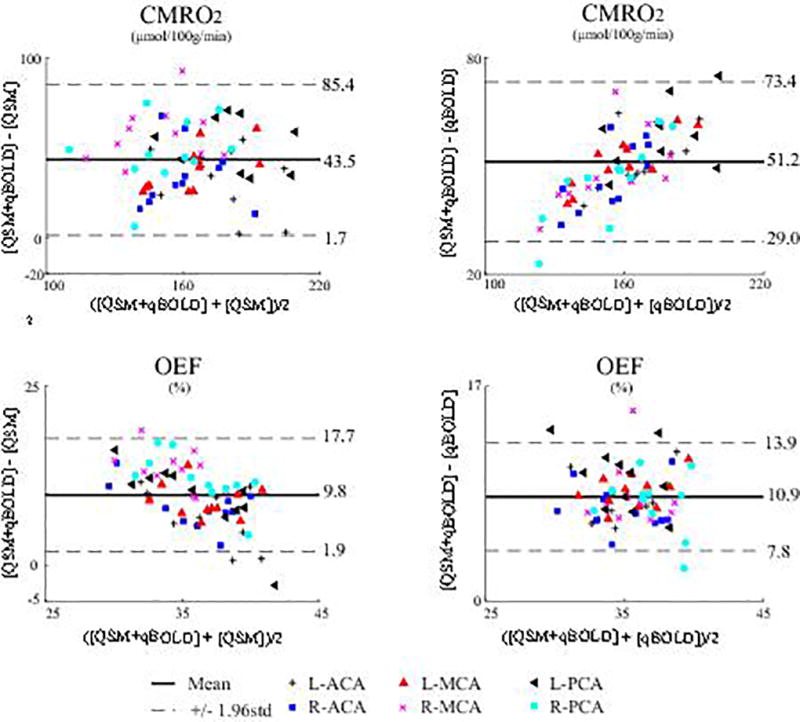
Bland-Altman plots comparing OEF and CMRO2 values in VT ROIs between QSM+qBOLD and the two reference methods, QSM and qBOLD. The mean differences are 43.5 µmol/100g/min (QSM vs QSM+qBOLD) and 51.2 µmol/100g/min (qBOLD vs QSM+qBOLD) for CMRO2 (p<0.01), and 9.8 % (QSM vs QSM+qBOLD) and 10.9 % (qBOLD vs QSM+qBOLD) for OEF (p<0.01).

DISCUSSION

Our results demonstrate the feasibility of a QSM+qBOLD method for mapping CMRO2 by comprehensive modeling of both the magnitude and phase of multi-echo gradient echo data. When either QSM modeling phase or qBOLD modeling magnitude are used individually to estimate CMRO2, a number of assumptions are required: a linear relationship between CBF and v and the minimum local variance of the estimated parameters within a tissue block for the QSM-based method (18), and constant non-blood tissue susceptibility for the qBOLD method (16,20). These assumptions may cause errors and are eliminated in the proposed QSM+qBOLD method.

Compared to QSM and qBOLD alone, the proposed QSM+qBOLD shows clearer GM/WM CMRO2 contrasts (Fig. 2), more uniform OEF compared to QSM (Fig. 3), and better agreement with results presented using other independent CMRO2 estimation methods such as PET (45). By overcoming the limited availability of PET, MRI provides greater accessibility for patient studies. Without any vascular challenge, QSM+qBOLD can be readily applied to study damage to vital organs caused by oxygen-deficiency, including Alzheimer’s disease (AD) (46,47), multiple sclerosis (48,49), and ischemia in stroke (1,50).

Compared to qBOLD, QSM+qBOLD shows higher OEF (Figs. 3, 4, and 5), with 39.3 ± 2.2 % for the whole brain; this is in a good agreement with results from previous PET studies which have OEFs of 35 ± 7 % (51), 42.6 ± 5.1 % (52), 41 ± 6 % (53), and 40 ± 9 % (54). This difference is not driven by venous blood volume (v), which was found to be similar between qBOLD and QSM+qBOLD (Fig. 3). Instead, the higher OEF may be explained by the inclusion of non-blood tissue susceptibility (χ_nb) as a variable, which, in qBOLD, is assumed to be equal to the susceptibility of fully oxygenated blood (χ_ba). The resulting χ_nb (−19.8 ± 3.5 ppb in CGM) is greater than χ_ba (−108.3 ppb). To obtain the same measured susceptibility difference δω in Eq. 5 when χ_ba − χ_nb < 0, the venous oxygenation Y needs to decrease, which leads to a higher OEF (Eqs. 2 and 5). This suggests that inclusion of χ_nb was a factor in the observed OEF increase.

QSM+qBOLD shows higher OEF average than QSM for whole brain (39.3 ± 2.2 % vs 34.5 ± 3.1 %). A likely cause of this may lie in the use of the global constraint in QSM (18), which is not used in QSM+qBOLD. The global constraint from straight sinus (SS) might not precisely estimate the average oxygentation in the whole brain because SS may not represent all the draining veins (55,56) that are known to have considerable variation, e.g. 47.7% ~ 75.3% (57).

At the GM/WM boundary in the CMRO2 map, the QSM method shows a sharp transition, whereas the QSM+qBOLD method reveals a gradual change (Figs. 2 and 3). The sharp GM/WM edge in QSM may be caused by separate optimization for the GM and WM (18); in the QSM+qBOLD method, the optimization was performed for whole brain. The CMRO2 GM/WM contrast in QSM+qBOLD is primarily driven by CBF since OEF map looks fairly uniform (Fig. 3). A lack of CMRO2 GM/WM contrast in QSM is not uniform and more prominent in areas where OEF appears underestimated (Figure 3, top and bottom left). Errors in GM/WM segmentation or smoothing by the MLV assumption may have caused these local underestimations.

The CMRO2 and OEF maps are smoother using the QSM method (Figs. 2 and 3). This may be caused by the use of MLV in the QSM method (18), which assumes that CMRO2 and χ_nb are constant within small blocks of brain tissue, to overcome the underdetermined system (2 unknowns and 1 equation per voxel) when no challenge is used. The MLV assumption in the QSM method is highly dependent on the block setting, e.g. block size and number of block shifts. The QSM+qBOLD model eliminates this MLV assumption using qBOLD modeling of the magnitude data.

The non-blood tissue susceptibility χ_nb shows a clear GM/WM contrast using QSM+qBOLD (Fig. 3). This is consistent with the difference in myelin content between CGM and WM (58).

The QSM+qBOLD model may still be affected by residual limitations in QSM and qBOLD models. The qBOLD term ignores the detailed microstructure of brain tissue, including myelin water components and magnetic anisotropy of myelin in white matter. The qBOLD Eq.4 may be expanded with 2 different R2s to account for myelin water, and fiber orientation dependent effects in Eq.5 to consider myelin magnetic anisotropy. The empirical L-curve analysis was used to determine relative weighting (w) in Eq.3. Additional studies are needed to investigate the influence of the weighting w, measurement error and differences in acquisition schemes. For instance, the propagation of bias and error in the estimated susceptibility into QSM+qBOLD measurments will depend on the choice of w. Spatial resolution will play a role in the choice of w: while smaller voxels typically improve QSM estimates (59), the resulting signal to noise ratio (SNR) loss may affect qBOLD estimates negatively, since it requires high SNR (16).

While QSM+qBOLD removed the linear CBF/CBV assumption in QSM and the constant non-blood tissue susceptibility assumption in qBOLD, it retains a constant ratio between venous and total blood volume (0.77), constant tissue hematocrit (0.357) and constant oxygenated heme molar concentration in the arteriole (7.377 µmol/ml) for the whole brain, which may vary among subjects and diseases. The ASL-measured CBF is known to contain errors, particularly in WM (60) and maybe deteriorated with the usage of shorter post-label delay in this study (1525 ms as used in the clinical protocol at our institution) than the recommended value of 2000 ms (32), which will propagate to CMRO2. The OEF and v estimation in large veins might be errorous because they were treated in the same way as normal brain tissue. This error could be suppressed using the v = 1 prior for large veins. The QSM+qBOLD optimization (Eq. 3) is non-convex, with convergence susceptible to dependency on solver implementation, initial guesses, parameter scaling, and stopping criterion. A reference standard such as ¹⁵O PET is needed to validate CMRO2 methods. Finally, the application of this method and its validation for a general patient population remains to be investigated.

In conclusion, our study demonstrated the feasibility of a comprehensive quantitative CMRO2 mapping method by combining QSM and qBOLD-based methods. In healthy subjects, the CMRO2 map obtained with QSM+qBOLD shows better GM/WM contrast as compared to an individual QSM or qBOLD-based method, while the OEF map appeared more uniform compared to the QSM-based method.

Supplementary Material

Supp TableS1

Supporting Table S1. CMRO₂ (µmol/100g/min) and OEF (%) for the cortical gray matter for 11 subjects (Mean ± Standard Deviation)

APPENDIX

In Eq. 4, the macroscopic field inhomogeneity contributing to the GRE signal (G) can be estimated via the voxel spread function (20,40,41):

$$G_n(\mathit{\text{TE}})=\frac{{\sum }_m|S_m({\mathit{\text{TE}}}_1)|·e^{(-R_{2,m}^{\ast }+i\gamma b_m)·\mathit{\text{TE}}}·{\prod }_{j=1}^3{\eta }_{\mathit{\text{nm}},j}}{|S_n({\mathit{\text{TE}}}_1)|·e^{-R_{2,n}^{\ast }·\mathit{\text{TE}}}}$$

where TE₁ is the first echo time, b_m is the average magnetic field in the voxel m, η_nm,j is the voxel spread function (the contribution of voxel m to voxel n) in jth direction (x, y, and z): η_nm,j = Σ_qj sinc (q_j − q_m,j (TE)) · e^{2πi·q_j(n−m)} where $q_{\mathrm{j}}=k_j·a_j,q_{\mathrm{m},\mathrm{j}}=\frac{(\gamma ·g_{m,j}·\mathit{\text{TE}}+{\varphi }_{m,j})·a_j}{2\pi }$, g_m,j and ϕ_m,j are the gradient of the background field and the first echo phase, respectively, and k_j is k-space $(-\frac{1}{2a_j}+\frac{1}{N_j·a_j},-\frac{1}{2a_j}+\frac{2}{N_j·a_j},\dots ,\frac{1}{2a_j})$, N_j and a_j are matrix size and voxel size in the jth direction, respectively.