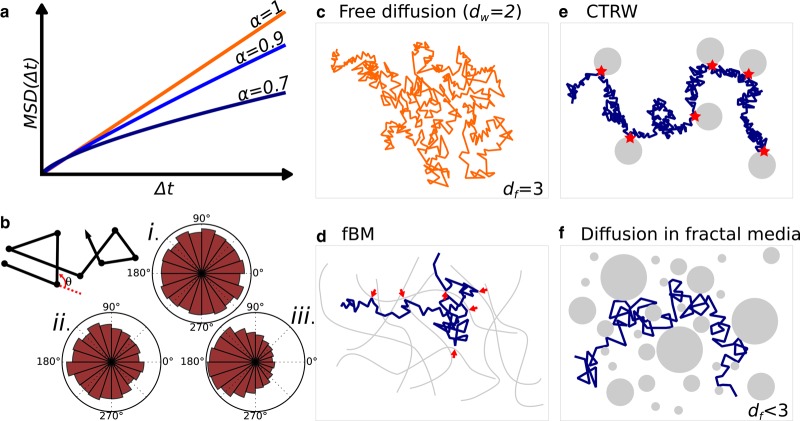
Figure 2. Models of anomalous diffusion and plausible underlying physical structures.

(a and b) Characterizations of anomalous diffusion. (a) Sub-linear mean-square displacement plotted as a function of time characterizes subdiffusion, and reflects how a diffusing particle explores space, the degree of anomalous diffusion is characterized by the exponent α, the lower the α the more subdiffusive the process. (b) Free diffusion is characterized by isotropic distribution of angles — subpanel (i) — whereas an anisotropic distribution indicates anomalous diffusion — subpanels (ii) and (iii). (c) 3D free diffusion ($d_w=2$), as usually encountered in a homogenous media ($d_f=3$). (d–f) Several types of heterogenous media can yield anomalous diffusion, including (d) diffusion within a viscoelastic polymer, in which a protein “bounces against” an elastic structure, a process traditionally described by fractional Brownian motion (fBm) and (e) free diffusion interspersed by long binding times — red stars, a process called CTRW, and (f) diffusion within a fractal media, that is a space obstructed by obstacles of all sizes.