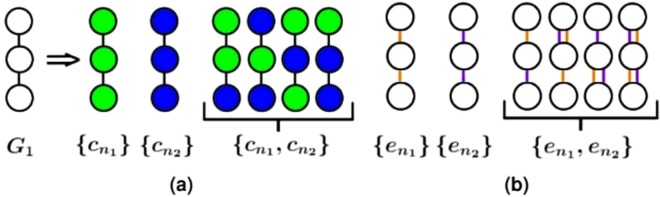
Figure 2.

Illustration of (a) node-colored and (b) edge-colored graphlets. (a) With the exhaustive approach for enumerating all possible heterogeneous graphlets corresponding to homogeneous graphlet G₁, i.e., a 3-node path, given two colors, there would be six heterogeneous graphlets, each accounting for both which colors are present in the graphlet and which node position has which color. On the other hand, with our approach, there are three possible colored graphlets, denoted by $\{c_{n_1}\}$, $\{c_{n_2}\}$, and $\{c_{n_1},c_{n_2}\}$, each accounting only for which colors are present in the graphlet, ignoring the node-specific color information. Consequently, with our approach, the last four graphlets on the right of the arrow, which all have the same two colors present in them, are treated as the same heterogeneous graphlet. We design our approach in this way primarily to reduce the time complexity of counting heterogeneous graphlets in a network (but consequently, we also reduce the space complexity compared to the exhaustive approach). Namely, with our approach, the computational time complexity of searching for a given colored graphlet in a heterogeneous network remains the same as that of searching for its homogeneous equivalent. This is because the former involves: 1) counting in the heterogeneous network all graphlets, independent of their colors (which is the same as counting homogeneous graphlets in the network), and 2) for each of the homogeneous graphlets found in the network, simply determining which node colors appear in it and thus which node-colored graphlet the non-colored graphlet corresponds to. Step 1 is the time consuming part of the node-colored graphlet counting process, unlike step 2, which is trivial (can be done in constant time). (b) We develop a similar approach for edge-colored graphlets.