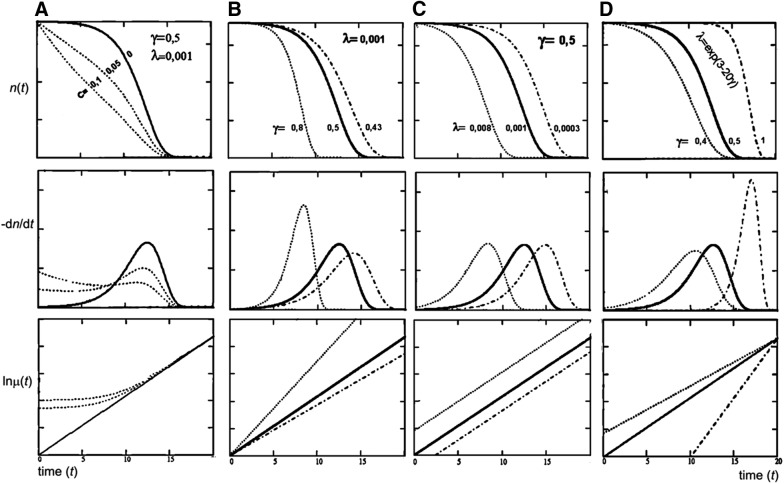
FIG. 5.

Illustrative plots of changes in lifespan depending on changes in the parameters of the Gompertz–Makeham law. Upper row: survivorship curves, n(t); middle row: age-at-death (lifespan) distributions, −dn/dt; lower row: logarithms of mortality force ln[−dn/(dt × n(t))]. Lifespan may increase because (A) the age-independent mortality C decreases; (B) the rate of aging γ decreases; or (C) the initial vigor (1/λ) increases. The column (D) shows a case when γ and λ are linked according to the SM correlation: greater initial vigor is associated with faster aging rate; for example, an increase in the availability or use of aerobic energy is associated with a greater rate of damage to macromolecules. On the semilogarithmic plots of μ versus t (the lower row), increases in C make the plots increasingly curved, changes in γ are manifested in plot slopes, and changes in λ in the parallel shifts of the plots, whereas negatively correlated changes in λ and γ make the plots converge. Note that when C is small, its changes may mimic patterns that correspond to the SM correlation. SM, Strehler–Mildvan.