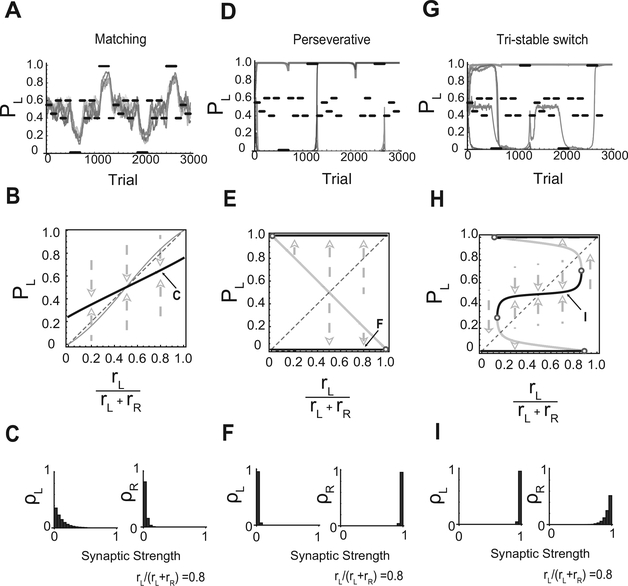
Figure 2:

The three regimes. (A-C) Matching regime. (A) Simulated dynamics of the choice probability P_L. The probability of baiting left is set to different values in different blocks of trials (solid black lines). The thick solid line represents P_L in different runs of simulations with the same parameters. In this regime, P_L tends to follow the changes in the baiting probability. (B) Equilibrium P_L versus the fractional baiting probability r_L/(r_L + r_R ). The thick solid line represents the stable equilibrium P_L, which in this regime it is approximately linear. The thin solid line represents the matching law. (C) The equilibrium distribution of the synaptic weights to the two-choice populations in the matching regime at the point indicated by C in panel B. (D-F) Same as in panels A-C but for the perseverative regime. (D) Now the simulated network tends to always choose the same target regardless the baiting probability. The chosen target depends on the initial conditions. Occasionally, for strongly biased baiting probabilities, the network switches target (see the vertical lines). (E) Now there are two stable equilibrium values for P_L (top and bottom solid horizontal lines). The thin solid line in the middle represents unstable fixed points of P_L and separates the two basins of attractions. (F) The distributions of the synapses are now skewed in opposite directions for the two populations of synapses. (G-I) Same as in panels A-C but for the tristable regime. (G) P_L is most of the time close to one of the three stable points (0, 0.5, 1). (H) For an extended range around a fractional baiting probability of 0.5, there are three stable and two unstable points. (I) The distribution of the synapses for the stable point around P_L = 0.5. The distributions for the other two stable points are similar to those of the perseverative regime. Parameters: (A) m = 2, T = 0.1, $\frac{{\alpha }_n}{{\alpha }_r}=1$, γ = 1, r_R + r_L = 0.35; (B) m = 50, T = 0.1, $\frac{{\alpha }_n}{{\alpha }_r}=0.1$, γ = 0.1, r_R + r_L = 1; (C) m = 50, T = 0.1, $\frac{{\alpha }_n}{{\alpha }_r}=0.01$, γ = 1, r_R + r_L = 1.