Abstract
Purpose
This study demonstrates a dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) estimate of tumor interstitial fluid pressure (TIFP) and hydraulic conductivity in a rat model of glioblastoma, with validation against an invasive ‘wick-in-needle’ (WIN) technique. An elevated TIFP is considered a mark of aggressiveness, and a decreased TIFP a predictor of response to therapy.
Methods
DCE-MRI studies were conducted in 36 athymic rats (controls and post-treatment animals) with implanted U251 cerebral tumors, and with TIFP measured using a WIN method. Employing a model selection paradigm and a novel application of Patlak and Logan plots to DCE-MRI data, MRI parameters required for estimating TIFP noninvasively were estimated. Two models, a fluid-mechanical model and a multivariate empirical model, were used for estimating TIFP, as verified against WIN-TIFP.
Results
Using DCE-MRI, the mean estimated hydraulic conductivity (MRI-K) in U251 tumors was (2.3 ± 3.1) × 10−5 [mm2/mmHg-s] in control studies. Significant positive correlations were found between WIN-TIFP and MRI-TIFP in both mechanical and empirical models. For instance, in the control group of the fluid-mechanical model, MRI-TIFP was a strong predictor of WIN-TIFP (R2 = 0.76, p<0.0001). A similar result was found in the bevacizumab-treated group of the empirical model (R2 = 0.93, p = 0.014).
Conclusion
This research suggests that MRI dynamic studies contain enough information to noninvasively estimate TIFP in this, and possibly other, tumor models, and thus might be used to assess tumor aggressiveness and response to therapy.
Keywords: Tumor interstitial fluid pressure, Tissue hydraulic conductivity, dynamic contrast enhanced MRI, DCE-MRI, Darcy’s law, Glioma
INTRODUCTION
Interstitial fluid pressure (IFP) is elevated in most solid tumors. This elevated pressure is due to the abnormal structure and function of tumor blood vessels, tumor lymphatics, and interstitium (1, 2). Experimental and clinical studies have demonstrated that increased tumor IFP (TIFP) reduces therapeutic efficiency (3, 4). TIFP is an independent prognostic parameter for tumor aggressiveness, tumor response, and treatment outcome (4, 5).
Both in animal (6) and human studies (7) TIFP is studied by such invasive methods as the wick-in-needle (WIN) technique. However, the WIN measurement is not easily repeated, and is clinically applicable only in locations where the tumor can be easily reached. Thus, developing a noninvasive and repeatable method to estimate TIFP as a biomarker in typically inaccessible brain tumors is a significant step forward in the assessment of tumor response to therapeutic interventions.
The noninvasive evaluation of TIFP using dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) has been explored in a limited number of studies. Pishko and colleagues (8) used a model of interstitial transport of contrast in porous media to estimate the flow and pressure of interstitial fluid, showing increased central TIFP and higher exudate streaming velocities at the tumor boundaries. However, these estimates lacked validation by invasive measurements. Hassid et al. (9), studying a mouse model of non-small-cell lung cancer used a slow infusion of the contrast agent gadolinium-diethylenetriamine pentaacetic acid (Gd-DTPA) into the blood for about 2 hours. They showed that parametric images of steady-state tissue Gd-DTPA concentration of the tumors and their surroundings reflected the spatial distribution of the IFP. However, the scaling methods outlined would make an absolute estimate of TIFP unreliable if the experiment were to be repeated in a different set of animals. Further, a study of this type is clearly impractical in human subjects, both because of the length of the study and the amount of contrast agent required.
Other DCE-MRI studies (10, 11) evaluated TIFP using parameters that related to tumor perfusion and permeability. However, the resulting estimates were not well correlated with needle-based TIFP measurements. Using a different approach, in a DCE-MRI experiment, the velocity of interstitial fluid flow along a line drawn normal to the tumor surface was proposed as a measure of central TIFP (12) but this approach may be unreliable if the velocity along different perpendiculars varies.
Herein two approaches using DCE-MRI to model TIFP are presented. The first approach is based on a well-recognized fluid-mechanical model of flow in porous media, while the second uses a multivariate analysis of MRI vascular parameters as predictors of TIFP to generate an empirical model. The fluid-mechanics approach demonstrates that, given good estimates for fluid-mechanical constants, the underlying physical mechanical system can be understood in the framework of classical poroelastic theory; the empirical approach confirms that MRI studies contain sufficient information to predict TIFP noninvasively.
The fluid-mechanical model for estimating TIFP depends on a measurement of the mean flux of a contrast agent (CA) at the tumor periphery. By Darcy’s law (13), this flux is driven by the IFP gradient at the tumor surface, and by such characteristics of the interstitium as porosity and interstitial hydraulic conductivity. Hydraulic conductivity will be estimated by using the Kozeny–Carman equation (14), and TIFP via Darcy’s law.
Both approaches to estimating TIFP include groups of animals with and without treatment and employ parameters produced by a model selection paradigm (15) and the Patlak and Logan plots applied to DCE-MRI data (16, 17). MRI-TIFP estimates are compared to WIN-TIFP measures performed immediately after the DCE-MRI study.
METHODS
The U251 Animal Model of Orthotopic Brain Tumor
These studies were conducted with the approval of the Institutional Animal Care and Use Committee. A U251 model of embedded cerebral tumor was studied in 36 athymic female rats (weight ~200g; Charles River, Wilmington, MA). Animals were anesthetized with isoflurane (4% for induction, 0.75 to 1.5% for maintenance, balance N2O:O2 = 2:1). The surgical zone was swabbed with Betadine solution, the eyes coated with Lacri-lube and the head immobilized in a small animal stereotactic device (Kopf Instruments, Tujunga, CA). After draping, a 1 cm incision was made 2 mm right of the midline and the skull was exposed. A burr hole was drilled 3.5 mm to the right of bregma, taking care not to penetrate the dura mater. A 10 µL Hamilton syringe with a 26 gauge needle (Model 701, Hamilton Co., Reno, NV) containing U251 tumor cells freshly harvested from log phase growth (5 × 105 in 10 µl of PBS) was lowered to a depth of 3.0 mm and then raised back to a depth of 2.5 mm to create a pocket. Cells were injected at a rate of 0.5 µL/10 s until the entire volume was injected. The syringe was then slowly withdrawn, the burr hole sealed with sterile bone wax and the skin sutured. Tumors in animals implanted following this technique grew to 3 to 6 mm diameter by about 18±3 days post-implantation.
Experimental Preparation and Protocol
About 18 days after implantation, rats underwent a high resolution T1-weighted MRI study to determine tumor size and tumor location. When tumors grew to about 6 mm in diameter (range ~ 3 to 8 mm), a DCE-MRI study was conducted in each animal, followed by the WIN TIFP measurement. A high resolution T2- weighted MRI after TIFP measurement verified that the needle path went through the tumor. Immediately after the T2-weighted MRI to determine the needle path, the animal was euthanized and its brain removed for histology.
In addition to studies in controls, in the course of other studies in tumors (18–20) a number of treatments were applied that generated variations in TIFP after treatment. Four groups of rats were studied: a control group (n = 13), a group treated with Bevacizumab (Avastin) (n = 9), a group treated with a combined therapy of Cilengitide and radiation therapy (RT) (n = 10), and an RT monotherapy group (n = 4). Bevacizumab was administered as a single dose i.v. for 30 minutes at dose of 10 mg/kg and delivered at selected time points of 2, 4, 8, 12, and 24 hours before the MRI study. In the combined therapy, Cilengitide was given as a single dose (4 mg/kg; intraperitoneal) prior to a 20 Gy single fraction radiation exposure as described previously (21). In the RT monotherapy group, RT was administered as a 10 Gy single dose of irradiation at selected time points of 24, and 48 hours before the MRI study(22).
MRI Studies
All MRI studies were performed using a 7 Tesla magnet in a Varian (Santa Clara, California) 20 cm bore system with a Direct Drive spectrometer and console. Gradient maximum strengths and rise times were 250 mT/m and 120 µs. All MRI image sets were acquired with a 32×32 mm2 FOV. The transmit coil was a RAPID (RAPID MR International, Columbus, OH) Quadrature Birdcage coil; the receive coil was RAPID two-channel phased-array surface coil for rat brain imaging. Arterial spin labeling (ASL), DCE-MRI, Look-Locker (LL), T1-weighted, and T2- weighted image sets were acquired and used to derive the tumor parameters that were used in both the fluid-mechanical model, and in multivariate empirical estimates of TIFP.
Spin-echo arterial spin-labeled (ASL) data was acquired to estimate cerebral blood flow in a single central slice, as previously described (23). MRI parameters were as follows: matrix = 128×64, one 1.0 mm slice, NA = 2, TE/TR= 24/1500. Arterial labeling = 1 sec.
The DCE-MRI sequence was a dual-echo gradient-echo (2GE) sequence that acquired three slices on 2 mm centers (1.8 mm slice, 0.2 mm gap). The slice set was centered on the tumor and 150 image sets at 4.0 s intervals were acquired with the following parameters: FA = 25°, matrix = 128×64, NE= 2, NA=1, TE1/TE2/TR = 2.0/4.0/60 ms. Total run time was about 10 minutes. At image 15 of the 2GE sequence Bolus injection of the CA (Magnevist, Bayer Healthcare Pharmaceuticals, Wayne, New Jersey), 0.25 mmol/kg at undiluted concentration, no flush, was performed by hand push.
Prior to the DCE-MRI sequence, and immediately after, two Look-Locker sequences (LL) sequences (FA = 15°, matrix 128×64, five 2.0 mm slices, no gap. NE=24 inversion-recovery echoes on 50 ms intervals, TE/TR=4.0/2000 ms) were run so that a voxel-by-voxel estimate of longitudinal relaxation time (T1) in the tissue could be made pre- and post-CA administration. Before the first LL sequence, a 6-image progressive saturation set of 2GE studies was run with varying repetition times and used, together with LL T1 maps, to independently estimate the FA used in the subsequent DCE-MRI experiment. The sequence parameters were as follows: (nominal) FA = 25° matrix = 128×64, three 1.8 mm slices, 0.2 mm gap, NE= 2, NA=1, TE1/TE2/TR = 2.0/4.0/(60, 100, 200, 300, 400, 600) ms.
Two high-resolution T1-weighted spin-echo images were acquired pre- and post-CA, to locate the tumor and its size, with the following parameters: FA = 45°, 180°, matrix 256×192, 27 slices, 0.4 mm thickness, 0.1 mm gap, NE = 1, NA = 4, TE/TR = 16/800 ms.
Two high-resolution T2-weighted spin-echo images were acquired pre-CA and post-TIFP measurement, (the latter to examine the needle track), with the following parameters: FA = 90°, 180°, matrix 256×192, 27 slices, 0.4 mm thickness, 0.1 mm gap, NE = 4, NA = 2, TE/TR = (20, 40, 60, 80)/3000 ms).
Tumor Vascular Parameters
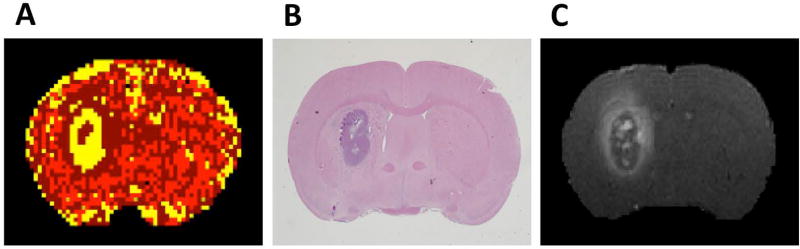
The DCE-MRI analysis employed to derive vascular parameters for estimating TIFP used a model selection paradigm (15) based on Patlak graphical methods (24, 25). Model selection generates maps of brain regions and labels them with the number of parameters used to describe the data. This results in regions with: i) Model 1 region: essentially normal vasculature with no leakage, where only filling of the vasculature with CA occurs; ii) Model 2 region: with measurable leakage from the microvasculature to the interstitial space, but lacking evidence of reflux of CA from the interstitial space to the vasculature; or iii) Model 3 region: highly leaky vessels with measurable reflux of CA from the interstitial space to the microvasculature - see Figure 1A. A model selection paradigm has the advantage, especially in the brain, that the border between tumor and surrounding normal tissue can be well defined by the spatially changing permeability of the tissue, with the tumor vasculature typically permeable to a contrast agent, and the normal tissue typically impermeable across the time of the 10-minute DCE-MRI study. Model selection was employed to describe the tumor region of interest (ROI), and to define an ROI of the tumor periphery consisting mostly of normal tissue. The analysis that estimated extracellular space in regions selected as Model 3 used an adaptation of the Logan graphical method (26) that has been verified, both against histology, and by comparison to similar estimates generated by the extended Tofts model (17). In all animals, post-contrast T1-weighted images and hematoxylin and eosin (H&E) stained sections confirmed that the tumor ROI that was defined by model selection (Figure 1B and 1C).
Figure 1.
A, a map of model selection, with the standard model and its nested sub-models as the set of possible analyses of DCE-MRI data: yellow = Model 3 (tumor ROI), dark red = Model 2 (IFP gradient region where fluid flows outward from tumor tissue to surrounding normal tissue), red = Model 1 region (normal brain tissue). B, H&E staining of a centrally located tissue slice approximately corresponding to the central slice of the MRI study. C, a high-resolution post-CA T1-weighted image. The enhanced contrast ring demonstrates the likely convection of the CA from the central lesion to the surroundings. Note the anatomical agreement in the position and distribution of the tumor mass and boundary between Model 3 region, T1 image, and H&E images. Also note the agreement between the enhanced ring in T1 and model 2 region.
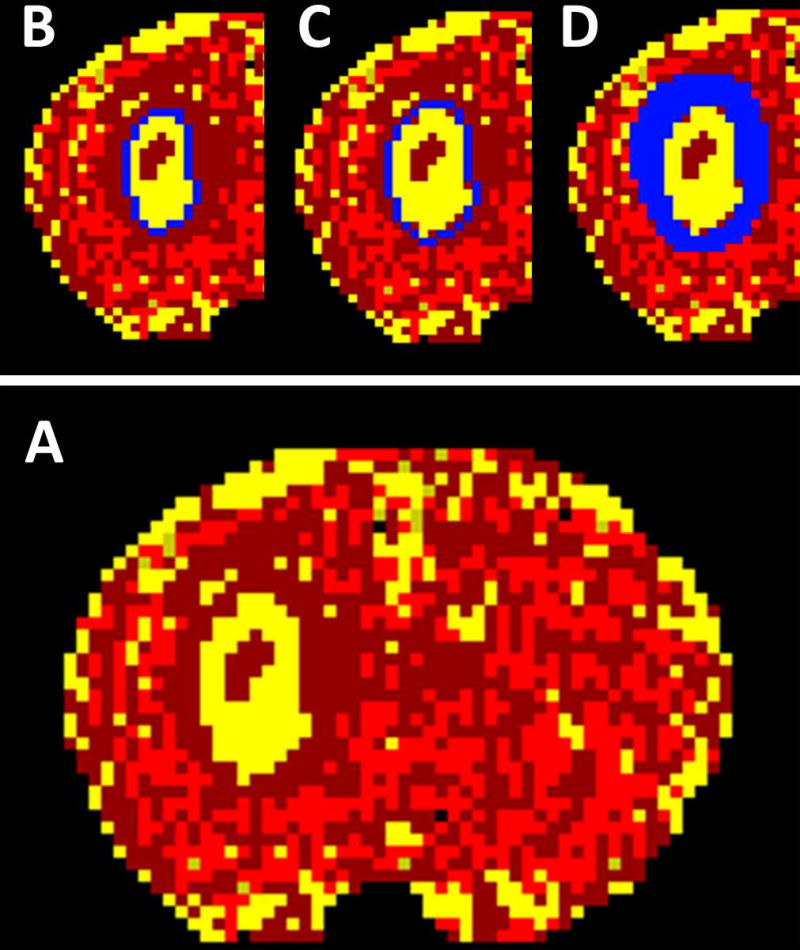
As in reference (16), MRI vascular parameters were estimated in three ROIs with differing physiologies; the whole tumor ROI, a one-pixel-wide ROI defining the leaky rim of the tumor, and a one-pixel ROI in the adjacent normal tissue immediately surrounding the tumor. MRI vascular and volume parameters used in estimating TIFP and associated with TIFP in the multivariate analysis were as follows: i) ASL for estimating tumor blood flow (TBF) (23) in the tumor itself, in the leaky rim of the tumor (TBF-rim), and in the adjacent normal tissue surrounding the tumor (TBF-peri); ii) Extended Patlak analysis (15) of DCE-MRI data to estimate the forward volume transfer constant (Ktrans) in the tumor, and in the tumor rim (Ktrans-rim); iii) Logan analysis (16, 17) of DCE-MRI data to estimate extracellular volume fraction (VD) in the tumor, extracellular volume fraction (VD-rim) in the leaky rim of the tumor, and extracellular volume fraction (VD-peri) in the mostly normal tissue immediately adjacent to the tumor (see below); and iv) a graphical method to estimate the flux of exudate fluid across the boundary of the tumor (see below). One direct benefit of model selection in and around the tumor is that an unambiguous delineation of the tumor extent is formed by the boundary of the Model 3 and Model 2 regions (figure 2).
Figure 2.
The model selection map with the regions of interest (ROIs) that were used in the estimation the MRI vascular parameters. A, as noted, yellow is Model 3 region (tumor ROI). B, a one-pixel-wide ROI defining the outer rim of the tumor representing the leaky rim of the tumor. C, a one-pixel-wide ROI immediately outside the Model 3 tumor rim ROI that is mostly normal tissue. D, a wide ROI outside the tumor ROI where the exudate flux at tumor boundary is estimated.
Reference (27) addresses the estimation of extracellular space in the mostly normal rim. It is assumed that contrast agent is not re-absorbed in the microvasculature of the mostly normal rim, and that at some time point in the experiment the concentration of contrast agent leaving the normal rim equilibrates with the concentration of contrast agent entering the normal rim. This assumption can be verified (and the time of equilibration identified) by use of a Logan plot, with the concentration of the inner adjacent tumor voxels used as the input function to the outer normal voxels. See figure 7 of reference (27) for an example of a curve fit that establishes an estimate of extracellular space in the normal rim of a tumor.
Using the same assumptions, a larger ROI can be drawn in the normal region around the tumor, and the accumulation of contrast agent can be followed over time. Again, using the inner adjacent tumor voxels as a forcing function, a Patlak-like plot can be constructed, the slope of which is the flow of tumor exudate into the ROI. A simple calculation for the area of the perimeter of the tumor yields flux from the tumor. See figure 8 of reference (27), and figure 9, showing the very highly correlated relationship (R2=0.9) between normal tissue compression and exudate flux.
WIN TIFP Measurement
TIFP was measured by inserting into the tumor a 23-gauge fluid-filled needle with a 2 mm-long side-port located about 3.5 mm from the needle tip. The distal section of about 1–2 cm of needle was filled with a polyester multifilament thread. The 23-gauge needle was connected directly to 1 ml plastic syringe through a Luer-Lock connection, and the syringe was coupled via about 20 cm of polyethylene tubing to a TruWave pressure transducer (model PX600F; Edwards Lifesciences LLC, Irvine, CA), and thence to a strain gage meter (model PAXLSG; Red Lion controls, York, PA). The needle and the polyethylene tubing were filled with artificial cerebrospinal fluid (ACSF) (150 mM Na, 3 mM K, 1.4 mM Ca, 0.8 mM Mg, 1.0 mM P, 155 mM Cl), and care was taken to eliminate all air bubbles within the system. Zero reference pressure was determined by placing the needle in a beaker filled with ACSF at the level of the needle insertion. The transducer and the strain gage meter were calibrated to provide 1 mV reading corresponding to 1mmHg.
The continuously anesthetized animal was removed from the MRI scanner for a WIN TIFP measurement. With the rat’s head immobilized on the same stereotactic device as used for tumor implantation, the WIN needle fixed vertically on the device and the pressure transducer located at the level of the rat’s head, a midline incision was made and the skull exposed. The WIN needle was inserted vertically into the tumor through the existing burr hole made for tumor cell implantation and advanced into the tumor in steps of 0.5 mm and held stationary in each step until the pressure reading stabilized, following which TIFP was recorded for about 2 min with a sampling rate of 1 reading per 5s. In this manner TIFP was measured along the tumor diameter, and the pressure-depth profile was established. Using the pressure-depth profile, TIFP values were averaged around the plateau region and the length of the pressure gradient was calculated as the distance of the increase in IFP from atmospheric pressure to plateau values. As noted, following the WIN-TIFP measurement, a second T2-weighted MRI was acquired to check that the path of the needle lay in the central slice of the DCE-MRI measurement. The needle path was also confirmed in the post-mortem histology slides.
Estimates of TIFP using the Darcy Equation (Fluid-mechanical Model)
It has been experimentally (28) and mathematically (29, 30) established that IFP in an embedded tumor is uniform and elevated throughout the tumor center and decreases steeply to normal tissue values at the tumor surface. Because interstitial flow occurs only in the presence of a pressure gradient, advection in the tumor occurs almost exclusively near the tumor surface, from the tumor periphery into the surrounding normal tissue (1). We assume the tumor to be a porous media with fluid transport in the tumor described by Darcy’s law (13).
Darcy’s law relates the IFP gradient and the velocity of exudate fluid at each point on the tumor surface through a local constant, the hydraulic conductivity, as follows:
| [1] |
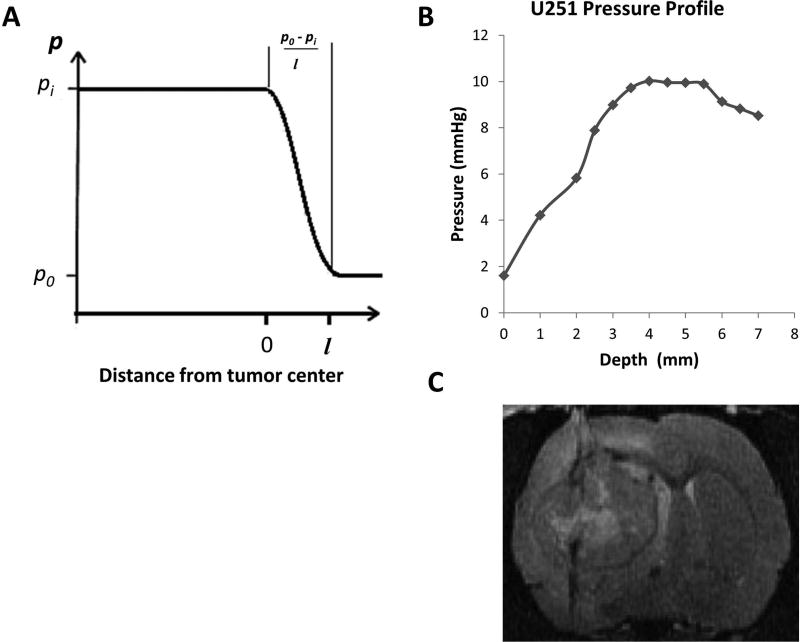
where: v is fluid velocity vector, ∇p is the pressure gradient vector, and K is the hydraulic conductivity of the tissue. In this paper, we will assume that conductivity is locally isotropic. A simplifying approximation for Darcy’s law was employed to estimate the central pressure of an embedded tumor; as shown in Figure 3A, Darcy’s law will be approximated across short distances as , where, pi is the TIFP, p0 is the IFP in the normal tissue, which is approximately at atmospheric pressure (4), and l is the length of pressure gradient. Thus, in order to estimate TIFP noninvasively, an estimate of the fluid velocity at the tumor surface and the hydraulic conductivity of the tissue are required.
Figure 3.
A, a schematic of the radial variation of IFP in model tumors. B, a pressure profile for U251 tumor showed a sharp peripheral gradient and central plateau, in agreement with theoretical studies of the spatial variation of TIFP that demonstrated the same central plateau and a sharp drop to normal at the boundary. C, High-resolution T2-weighted image acquired post TIFP measurement showing the needle track through the tumor mass.
Hydraulic conductivity depends mainly on the porosity of the medium and the viscosity of the fluid passing through the pores (14). It quantifies the ability of a porous medium to transmit fluids through its interconnected pores or channels when the fluid experiences a pressure gradient. Hydraulic conductivity depends on a combination of several microstructural parameters, including porosity, pore or grain size, and tortuosity (1). It can be viewed as a system property of a biological tissue, and can be described by the well-known Kozeny– Carman (KC) equation (14)
| [2] |
where, φ is the porosity and μ is the viscosity of the interstitial fluid; μ ranges from 3–3.5 × 10−3 Pa.s (31); a value of 3.5×10−3 Pa.s was employed. C is the Kozeny– Carman constant; it depends on porosity and is approximately equal to 5 for φ < 0.7 (Reference (14), p 442); a value of 5.0 was employed. The parameter S is the total specific surface area of the porous media.
The total specific surface area (S) is defined as the area of the surface that is exposed to the fluid per unit bulk volume. S depends on the geometrical structure of the pores, and has been commonly related to pore or grain diameters (14). S of a porous material can be affected by porosity, packing mode, grain size and shape (32). In our case, the material defining the grains consists of the cells and the extracellular matrix (ECM) of the tumor tissue, rendering an estimate of S on the basis of shape infeasible. Estimating the grains’ surface area based only on the cells’ surface area will underestimate S, and thus bias high the estimated hydraulic conductivity. To add difficulty, we have found no estimate of S in the literature. Accordingly, to approximate S values in the U251 tumor control sample, the KC equation was incorporated in Darcy’s law, and a regression analysis was applied to the quantities vs pi with the intercept set to zero. In this case S equals the square root of the reciprocal of the slope. Using control sample experimental measures of WIN-TIFP, and MRI estimates of v and φ, the value of S was calculated. As a first-order comparison, these estimates of S produced were checked against the mean of S calculated from the range of previously reported hydraulic conductivity values (33, 34) to account for the variation in S across tumors, using eq. [2] and the tumor porosity reported in each study.
After determining the value of S in the region of interest (ROI) of the tumor, and using the previously acquired experimental estimates of porosity (17), the hydraulic conductivity (MRI-K) was derived using the KC relationship. Using the methods of reference (16), the mean velocity of exudate fluid (v) across the surface of the tumor was estimated. Using the pressure-depth profile, the length of the pressure gradient was calculated. Thus, by Darcy’s equation, the necessary parameters to estimate TIFP noninvasively were on hand.
We note that fluid velocity was estimated via an estimate of flux in the mostly normal rim of the tumor (see the response to 1.5 above). Conductivity was estimated from DCE-MRI measures in the tumor itself. Thus, different regions were used to estimate these two parameters, and the concern that a single data set was overfitted is substantially diminished.
Regression of MRI Measures of Tumor Physiology against WIN-TIFP (Empirical Model)
We had on hand a number of MRI measures of tumor physiology, many of which might be considered relevant to fluid supply to the tumor, fluid drainage from the tumor, and/or resistance to interstitial flow in and around the tumor. We considered the following parameters: flow, i.e. perfusion as measured by ASL, in the tumor ROI (TBF); flow in the rim of the tumor (TBF-rim); flow in the mostly normal surround of the tumor (TBF-peri); transfer constant in the tumor ROI (Ktrans); transfer constant in the tumor rim (Ktrans-rim); extracellular volume fraction in the tumor ROI (VD); extracellular volume fraction in the tumor rim (VD-rim); extracellular volume fraction in the mostly normal surround to the tumor (VD-peri); and average interstitial fluid velocity at the rim of the tumor (v).
WIN-TIFP measures were tested for normality; when the Shapiro-Wilk test demonstrated a non-normal distribution in WIN-TIFP, the values were log-transformed. A multivariate analysis on the log-transformed data was performed to test for a set of MRI vascular parameters that best predicted (the log of) WIN-TIFP in the tumor. The best predictors to describe TIFP were chosen based on the Akaike information criterion (AIC). The data were analyzed as one set, taking into account the effect of the different treatment groups represented by indicator variables - i.e. each treatment group had its own intercept in the model.
After determining the best predictors of log TIFP, a regression analysis was applied using these predictors and the regression coefficients of these parameters were obtained. An empirical model for estimating TIFP (MRI-TIFPE) was established for the whole data set, and separately for each group. The model fits were verified against the WIN-TIFFP by a cross-validation leave-one-out method. Coefficients of determination as estimated by cross-validation (using the R package cv.lm (35)) are also reported. A secondary analysis with WIN-TIFP not log-transformed was also conducted but is not reported, since it resulted in essentially the same outcomes as in the main analysis.
Statistical Methods
All statistics are reported as mean ± standard deviation. The R Statistical Environment (36) was used for all statistical analyses. An initial analysis for correlation between the WIN-TIFP and MRI-TIFP estimates was performed using linear and multiple linear regression, followed by a leave-one-out cross-validation. The coefficient of determination (R2) was calculated by a simple regression followed by a leave-one-out cross validation using a linear model (routine cv.lm in the R statistical package). A Shapiro-Wilk test was used to test normality. A p-value ≤ 0.05 was considered statistically significant.
RESULTS
WIN-TIFP Measurements and Profiles
WIN-TIFP measurements were performed on 36 animals. TIFP was recorded as a function of tumor depth, and the pressure-depth profile was created for each animal. TIFP rose rapidly in the tumor periphery, reached a maximum value, and remained relatively uniform throughout the tumor; these results closely resembled those of previous investigators (28, 37). Figure 3B shows a representative pressure profile (A representative profile in normal tissue is shown as Figure 1S in the Supplemental Material). In typical measurements in tumors, a sharp increase in IFP from atmospheric pressure to plateau values was within 1.0 to 2.5 mm of the tumor boundary, with a mean of 1.66 ± 0.48 mm. TIFP values were averaged around the plateau region for each animal, the sample mean of TIFP for the control group was 6.0 ± 3.7 mmHg with range of 1.6 to 14.9 mmHg.
DCE-MRI Estimates of Hydraulic Conductivity
In order to estimate hydraulic conductivity of the tumor as described in equation [2], the total specific surface area of the cells and ECM, and the tumor porosity were estimated. An estimate of S that included both cells and ECM was generated by regressing flux versus central pressure and applying equation [2]. The slope of the regression analysis with the intercept set to zero for the experimental data was 4.8 × 10−7 mm2, yielding an estimate for S of 1443 mm−1 in the control group. This value is in approximate agreement with the mean S (~1400 mm−1.) calculated from previously reported hydraulic conductivities and porosities in other tumors (33, 34).
By using an individual animal’s estimate of porosity and the group S value in equation [2], the hydraulic conductivity was calculated for each animal; the mean estimated hydraulic conductivity (MRI-K) was (2.3 ± 3.1) × 10−5 [mm2/mmHg-s] for the control group, in general agreement with other reports in other tumor models (33, 34, 38, 39). Table 1 summarizes tumor parameters for the control group.
Table 1.
Tumor vascular parameters for U251 tumor control group.
| Parameters | Control (n = 13) | |
|---|---|---|
| Mean ± SD | Range | |
| Porosity % | 16.5 ± 5.8 | 9 to 32 |
| Exudate fluid velocity mm/s | (5.1 ± 2.5) × 10−5 | 1.1×10−5 to 8.5×10−5 |
| MRI-K mm2/mmHg-s | (2.3 ± 3.1) × 10−5 | 2.8×10−6 to 1.2×10−4 |
Darcy’s Estimates of TIFP (fluid-mechanical model)
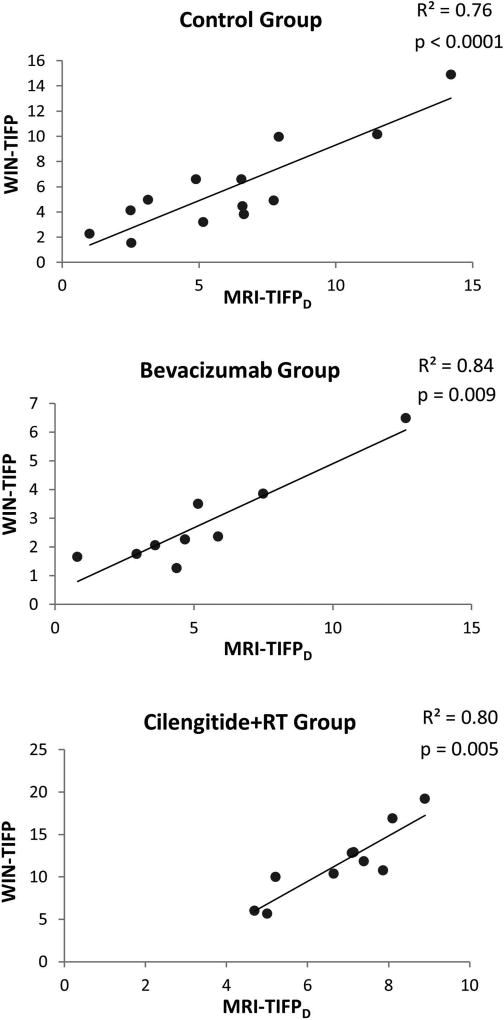
By using the mean estimated exudate fluid velocity at the tumor surface and the estimated MRI-K for each animal in the simplified form of Darcy’s law, MRI-TIFPD was calculated for all groups except the RT group, where the sample size was too small to yield a reliable result. A GLM regression analysis was applied for each group. Significant correlations were found between WIN-TIFP and MRI-TIFPD in all groups as shown in Figure 4. In the control group, a strong positive correlation was found, with an R2 of 0.76; GLM analysis showed MRI-TIFPD to be a strong predictor of WIN-TIFP (p<0.0001). Similarly, in the bevacizumab and Cilengitide+RT groups, MRI-TIFPD was highly correlated with WIN-TIFP with R2 = 0.84 (p = 0.009), and R2 of 0.80 (p = 0.005), respectively.
Figure 4.
WIN-TIFP versus MRI-TIFPD based on the fluid-mechanical model for U251 tumor groups; control, bevacizumab, and Cilengitide+RT. All groups showed significant positive correlations.
Multivariate Analysis and regression of WIN-TIFP and MRI Vascular Parameters (Empirical Model)
A multivariate analysis for log(WIN-TIFP) and the MRI vascular parameters, TBF, TBF-rim, TBF-peri, Ktrans, Ktrans-rim, VD, VD-rim, VD-peri, and v, was applied. These parameters were estimated in the three different ROIs as described in Figure 2 (whole tumor, tumor rim, tumor periphery) that are believed to have different physiological characteristics and may affect TIFP differently. AIC was used as a selection method to determine which set of these tumor parameters was the best predictor of TIFP. There were four parameters that best described TIFP and had the lowest AIC value (AIC = 37.7), compared to the complete model (AIC = 45.1), or to each parameter alone. These tumor parameters were VD in the tumor (p = 0.0002), v at the tumor surface (p = 0.006), TBF-peri in the adjacent normal tissue surrounding the tumor (p = 0.017), and TBF in the tumor (p = 0.052).
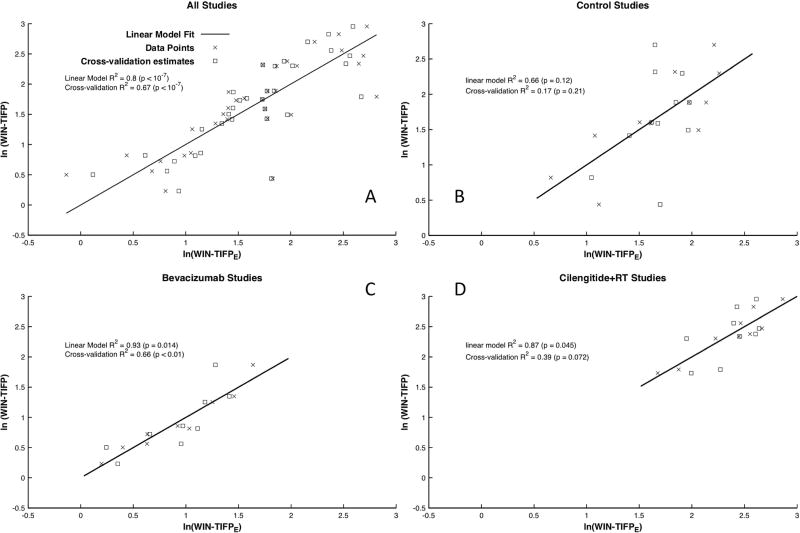
Based on the result of the multivariate analysis, an empirical model for estimating log TIFP was established (MRI-TIFPE) consisting of linear regression of the above four parameters. A regression analysis of these predictors on the entire data set was performed, yielding regression coefficients as follows: VD in the tumor (−7.6), v at the tumor surface (157), TBF-peri in the adjacent normal tissue surrounding the tumor (−0.0119), TBF in the tumor (0.0113), and intercept (2.55). The R2 for the linear regression analysis was 0.8 (p < 10−6). Results of a cross-validation leave-one-out analysis (re-estimation of log(MRI-TIFPE) for each point with that point omitted from the regression model) are shown in Figure 5A. A leave-one-out cross-validation analysis yielded an R2 of 0.67 (p < 10−6). Thus, it can be said with some confidence that noninvasive DCE-MRI and perfusion measures combined contain sufficient information to predict TIFP.
Figure 5.
log(WIN-TIFP) versus log(MRI-TIFPE) based on the empirical model for A) all U251 tumor groups, B) control, C) Bevacizumab, and D) Cilengitide+RT. The all-tumor-groups, Bevacizumab and Cilengitide+RT groups showed significant positive correlations. Leave-one-out cross-validation estimates at the observed points are plotted as hollow boxes. R2 and p-values for the linear regression, and for the cross-validation are reported for all groups, and for each group with more than 4 members. The group “RT alone” is not shown, since it contained only 4 members.
The subgroups were examined with a similar linear regression analysis that used the same four parametric predictors as in the combined analysis (VD, v, TBF-peri, and TBFtumor), with a separate log(MRI-TIFPE) constructed for each subgroup. Even in these relatively small groups (N = 11, 9, and 9 for controls, Avastin, and Cilengitide+RT, respectively, where the sample size for Cilengitide+RT was reduced by one due to missing values for blood flow), some significant correlations were found between log(WIN-TIFP) and log(MRI-TIFPE) as shown in Figures 5B – 5C. In the control group, despite an R2 of 0.66, the relationship was not significant (p = 0.12). The cross-validation study confirmed this result (R2 = 0.17, p = 0.21). However, in the Bevacizumab group, log(MRI-TIFPE) remarkably predicted log(WIN-TIFP) with an R2 of 0.93 (p = 0.014). The cross-validation study maintained this result (R2 = 0.66, p < 0.01). In the Cilengitide+RT group, log(MRI-TIFPE) predicted log(WIN-TIFP) with an R2 of 0.87 (p = 0.045), somewhat weakened by the cross-validation study (R2 = 0.39, p=0.072).
DISCUSSION
Two approaches to the problem of noninvasively estimating TIFP have been presented, the first a model-based approach that utilizes well-established fluid-mechanics theory, and the second an empirical approach that tests measures that might contribute to measured TIFP.
The mean plateau TIFP pressure was quite variable (1.6 to 14.9 mmHg) across animals. The central TIFP of an embedded tumor depends on sources and sinks (30). Sources are affected by perfusion pressure, local tumor blood flow, vascular resistance, TIFP itself, and vascular permeability. Sinks are affected by tumor size, tumor extracellular space, peritumoral compression, and probably such other factors as intracerebral fluid pressure and venous reabsorption. The measured TIFP is a complex function of all these terms. Both models of TIFP point to the distribution volume, VD, as a principal factor in determining TIFP. In the deterministic Darcy model, VD (i.e. porosity, φ) is identified as an essential element in calculating the tissue fluid conductivity, and thus is essential to describing the flow of interstitial fluid to its sink. In the empirical model, we see that two source terms, flow in the tumor periphery, and flow in the tumor itself, were added to VD in order to predict the central TIFP. It appears that tumor growth rate, reflected in VD, is a major factor determining TIFP, and it also appears be that tumor metabolic demand, reflected in perfusion, is also a determinant of TIFP.
In the fluid-mechanical approach, a noninvasive DCE-MRI method for estimating hydraulic conductivity and TIFP in a rat model of embedded cerebral tumor is presented. The method is based on the theory of fluid convection in porous media and uses previously presented methods for estimating tumor porosity (17) and exudate fluid velocity at the tumor periphery (16). Hydraulic conductivity was estimated by using the KC equation (14), and TIFP was estimated via Darcy’s law. Estimates of TIFP were performed in a U251 rat model of cerebral glioblastoma, with and without treatment intervention to create variations in TIFP across the sample of animals. Invasive WIN TIFP measurements were performed immediately after the DCE-MRI study in all rats in order to verify MRI-TIFP estimations.
Previous measurements of the hydraulic conductivities of tumors are limited due to the experimental difficulties in evaluating this parameter, with in vitro estimates generated by applying Darcy’s law (40, 41), and more recently ex-vivo by confined compression tests (33). A few studies have attempted an in vivo estimate of hydraulic conductivity (38, 41, 42). However, most of these in vivo estimates were not straightforward, due to the difficulties of defining the geometric tissue dimensions.
In general, hydraulic conductivity has been expressed as a function of porosity. In particular, the KC equation, a widely accepted model for estimating hydraulic conductivity, has depended mainly on porosity, with most parameters such as specific surface area, tortuosity, and shape factor related to porosity (32). Herein, the estimated MRI-K values for U251 tumors were in the range of estimates in other tumors (33, 34, 38, 39). The mean of MRI-K in the control group was (2.3 ± 3.1)×10−5 [mm2/mmHg-s]. However, Table 1, showed a wide range of the MRI-K values among studies, reflecting the dependency of MRI-K on the porosity of each individual tumor and showing the important contribution of the extracellular matrix to the hydraulic conductivity.
Since we had no direct in vivo estimates for the total specific surface area, there was some limitation in estimating MRI-K. Commonly, in studies of filtration in porous media, the surface area is calculated by using the grain dimensions; however, in the case of tissue, surface area is dependent on the wetted surface of the cells, plus that of the ECM. A consideration of only the cell dimensions will result in an overestimation of hydraulic conductivity. Our data from the control sample showed that S was variable across tumors with range of 1091 to 2169 mm−1. Using the group mean to construct an approximate estimation of S across the U251 tumors, while our best available strategy for approaching the problem of estimating TIFP via the Darcy approach, did probably introduce a range of errors into the estimates thereby generated..
Some estimate of relative wetted surface area in tumors should be included in future experimental approaches to TIFP estimates. MRI contrast mechanisms, T1, T2, and T2* depend on the interaction between the solid tissue compartment and the liquid compartment, and that interaction is strongly dependent on the amount of surface that the mobile protons of the liquid compartment experience. For instance, the forward magnetization transfer ratio is strongly dependent on the amount of free water, compared to the amount of protein, in a given tissue (43). This generates the possibility that, given a calibration for surface area by some other means, the magnetization transfer ratio might serve as a surrogate measure of wetted surface area in tissue, albeit that estimate would have to be adjusted for intracellular/extracellular moieties.
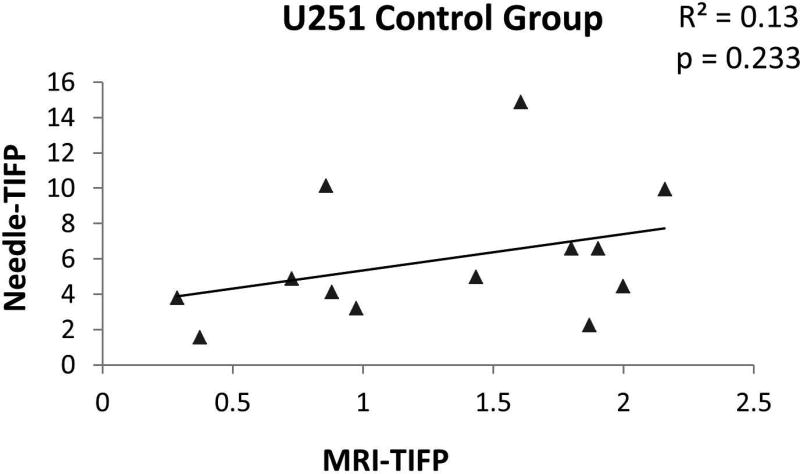
TIFP has been evaluated noninvasively using DCE-MRI in a limited number of studies (8, 9); these attempts assumed tumor models with fixed porosity and hydraulic conductivity. Neglecting the individual tumor’s differences in hydraulic conductivity in determining TIFP may lead to substantial systematic errors in estimation of TIFP. For instance, Figure 6 displays a poor correlation between the MRI-TIFP and WIN-TIFP when a fixed value of hydraulic conductivity was applied instead of the porosity-adjusted MRI-K. Contrariwise, our estimate of MRI-TIFPD showed good correlations with the WIN-TIFP (Figure 4), showing that hydraulic conductivity estimated from the measured porosity of the tissue is an essential factor in estimating TIFP. These results were supported by the multivariate analysis of WIN-TIFP showing that VD in the tumor (i.e., tumor porosity), the main factor in estimating hydraulic conductivity, was found to be the tumor parameter to most descriptive of TIFP (p = 0.0002).
Figure 6.
WIN-TIFP versus MRI-TIFP for the control group. A fixed value of hydraulic conductivity was applied in the model instead of the estimated MRI-K to estimate MRI-TIFP. Note the poor correlation indicating that hydraulic conductivity is an important factor in estimating TIFP. The hydraulic conductivity value that used here was from Netti et al. (33) for U87 glioma.
In this model of cerebral glioma, significant results were found in all groups. The estimated MRI-TIFPD in the control group was a strong predictor of WIN-TIFP with p<0.0001. After interventions with two different treatments, bevacizumab and combined therapy of Cilengitide and RT, the same strong correlations between MRI-TIFPD and WIN-TIFP was found with p= 0.009 and p=0.005 respectively.
However, our estimates, while highly correlated, systematically underestimated TIFP in the bevacizumab and Cilengitide+RT groups. It may be that, since the specific surface area was estimated from the control group and then applied in the treated groups, the specific surface area was affected by the applied treatments, and in turn affected the estimates of the individual MRI-K. Another explanation is provided by the multivariate analysis, which showed that, besides porosity and fluid exudate velocity at the tumor surface, WIN-TIFP was significantly predicted by the TBF-peri, i.e. flow in the normal tissue surrounding the tumor and TBF in the tumor itself, implying that adding latter two parameters in the MRI-TIFPD estimating model might yield better estimates.
We have noted that it is unlikely that overfitting of data occurred when estimating tumor porosity and exudate fluid velocity. More generally in order to estimate vp, Ktrans, and kep, extended Patlak (i.e., extended Tofts) models require tissue concentration to change in both first and second derivatives; the tissue concentration has to be changing in relation to the vascular concentration. Logan estimates of extracellular space require that an equilibrium exchange be established between the vascular concentration and the extravascular concentration. These two approaches utilize different segments of tissue concentration data – the Patlak model draws information from the early, rapidly changing segment, while the Logan model draws information from the later, equilibrated segment. While the two approaches do use the same data, it seems unlikely that overfitting occurs. A check against overfitting is supplied by the empirical model, which systematically eliminates variables that do not contribute significantly and uniquely to the description of the data.
In the empirical approach, when terms that reflected fluid sources were added to those of the Darcy model, significant results were found in the entire population, and in Bevacizumab and Cilengitide+RT subgroups (Figures 5A, C, D). The estimated log(MRI-TIFPE) was a predictor of log(WIN-TIFP) in both groups, despite the small sample sizes of those groups. These relations persisted under a more rigorous cross-validation study.
There may be a concern that the administration of Bevacizumab suppresses evidence of contrast agent leakage to such an extent that the experimental methods outlined herein are invalidated. However, it appears that the U251 glioma in the rat cerebral vascular behaves differently from human gliomas after Bevacizumab; although Ktrans does decrease, we see no evidence of a wholesale suppression of vascular permeability (see Fig 2S, Supplemental Material). In the empirical approach, WIN-TIFP correlated highly with estimates of TIFP in the Bevacizumab group. It may be that effects not included in the main empirical model were diminished by the treatment, and that this improved its predictive ability. One possibility is that a decrease in the vascular re-absorption of contrast agent in the vasculature of the mostly normal rim of the tumor increased the fidelity of the model, since vascular re-absorption and (probably) more rapid clearance was not reflected in the measures being made.
As noted, R2 for all models decreased (as expected) in all the cross-validation studies, but the general impression remains that there is sufficient information in noninvasive MRI studies to reliably predict tumor interstitial fluid pressure in this tumor model, and possibly in other tumors with similar characteristics. A note of caution is necessary. In vascular beds other than cerebral, where Ktrans is more strongly related to perfusion, some weightings may change. Since Ktrans, whether diffusion-limited or not, is a measure of fluid delivery to the tumor, it would be an important contributor to the TIFP if perfusion weighted more significantly in its value. In that case, in an empirical approach, it might be that the source term in the source minus sink balance would have to include Ktrans, with perfusion in the tumor and rim not as heavily weighted as in cerebral tumors. For future work, a more complete model that considers tissue compression, perfusion, and permeability is likely needed to fully describe fluid mechanics in solid tumors.
In summary, MRI-TIFP estimates constructed by using fluid-mechanical and empirical models were generally well correlated with WIN-TIFP measures. It is likely that a more complete poroelastic model that considers both sources (perfusion, permeability) and sinks (porosity, local pressures) can yield a noninvasive estimate of TIFP in both controls and treated groups.
Supplementary Material
Acknowledgments
The authors thank Ms. Jun Xu for her superb technical assistance. Research reported in this publication was supported by the National Cancer Institute of the National Institutes of Health under award number R01CA135329 (JRE). The content of this article is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Grant sponsor: National Institutes of Health; Title: MRI Biomarkers of Response in Cerebral Tumors; Grant number: R01 CA135329 (JRE).
References
- 1.Jain RK. Transport of molecules in the tumor interstitium: a review. Cancer Res. 1987;47(12):3039–51. Epub 1987/06/15. [PubMed] [Google Scholar]
- 2.Wiig H, Rubin K, Reed RK. New and active role of the interstitium in control of interstitial fluid pressure: potential therapeutic consequences. Acta anaesthesiologica Scandinavica. 2003;47(2):111–21. doi: 10.1034/j.1399-6576.2003.00050.x. [DOI] [PubMed] [Google Scholar]
- 3.Heldin CH, Rubin K, Pietras K, Ostman A. High interstitial fluid pressure - an obstacle in cancer therapy. Nat Rev Cancer. 2004;4(10):806–13. doi: 10.1038/nrc1456. Epub 2004/10/29. [DOI] [PubMed] [Google Scholar]
- 4.Lunt SJ, Fyles A, Hill RP, Milosevic M. Interstitial fluid pressure in tumors: therapeutic barrier and biomarker of angiogenesis. Future oncology (London, England) 2008;4(6):793–802. doi: 10.2217/14796694.4.6.793. Epub 2008/12/18. [DOI] [PubMed] [Google Scholar]
- 5.Rofstad EK, Gaustad J-V, Brurberg KG, Mathiesen B, Galappathi K, Simonsen TG. Radiocurability is associated with interstitial fluid pressure in human tumor xenografts. Neoplasia (New York, NY) 2009;11(11):1243–51. doi: 10.1593/neo.91152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wiig H, Reed RK, Aukland K. Measurement of interstitial fluid pressure in dogs: evaluation of methods. The American journal of physiology. 1987;253(2 Pt 2):H283–90. doi: 10.1152/ajpheart.1987.253.2.H283. [DOI] [PubMed] [Google Scholar]
- 7.Boucher Y, Kirkwood JM, Opacic D, Desantis M, Jain RK. Interstitial hypertension in superficial metastatic melanomas in humans. Cancer Res. 1991;51(24):6691–4. [PubMed] [Google Scholar]
- 8.Pishko GL, Astary GW, Zhang J, Mareci TH, Sarntinoranont M. Role of convection and diffusion on DCE-MRI parameters in low leakiness KHT sarcomas. Microvasc Res. 2012;84(3):306–13. doi: 10.1016/j.mvr.2012.09.001. [DOI] [PubMed] [Google Scholar]
- 9.Hassid Y, Furman-Haran E, Margalit R, Eilam R, Degani H. Noninvasive magnetic resonance imaging of transport and interstitial fluid pressure in ectopic human lung tumors. Cancer Res. 2006;66(8):4159–66. doi: 10.1158/0008-5472.can-05-3289. Epub 2006/04/19. [DOI] [PubMed] [Google Scholar]
- 10.Ellingsen C, Walenta S, Hompland T, Mueller-Klieser W, Rofstad EK. The microenvironment of cervical carcinoma xenografts: associations with lymph node metastasis and its assessment by DCE-MRI. Translational oncology. 2013;6(5):607–17. doi: 10.1593/tlo.13313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Haider MA, Sitartchouk I, Roberts TP, Fyles A, Hashmi AT, Milosevic M. Correlations between dynamic contrast-enhanced magnetic resonance imaging-derived measures of tumor microvasculature and interstitial fluid pressure in patients with cervical cancer. J Magn Reson Imaging. 2007;25(1):153–9. doi: 10.1002/jmri.20795. [DOI] [PubMed] [Google Scholar]
- 12.Hompland T, Ellingsen C, Ovrebo KM, Rofstad EK. Interstitial fluid pressure and associated lymph node metastasis revealed in tumors by dynamic contrast-enhanced MRI. Cancer Res. 2012;72(19):4899–908. doi: 10.1158/0008-5472.CAN-12-0903. Epub 2012/10/03. [DOI] [PubMed] [Google Scholar]
- 13.Nield DA, Bejan A. Convection in Porous Media. 3. Springer Science; New York, N.Y: Springer Science+Business Media, Inc; 2006; 2006.. 3rd ed. [Google Scholar]
- 14.Truskey GA, Yuan F, Katz DF. Transport Phenomena in Biological Systems: Pearson Prentice Hall. 2010 [Google Scholar]
- 15.Ewing JR, Bagher-Ebadian H. Model selection in measures of vascular parameters using dynamic contrast-enhanced MRI: experimental and clinical applications. NMR in biomedicine. 2013;26(8):1028–41. doi: 10.1002/nbm.2996. Epub 2013/07/25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ewing JR, Nagaraja TN, Aryal MP, Keenan KA, Elmghirbi R, Bagher-Ebadian H, et al. Peritumoral tissue compression is predictive of exudate flux in a rat model of cerebral tumor: an MRI study in an embedded tumor. NMR in biomedicine. 2015;28(11):1557–69. doi: 10.1002/nbm.3418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Aryal MP, Nagaraja TN, Keenan KA, Bagher-Ebadian H, Panda S, Brown SL, et al. Dynamic contrast enhanced MRI parameters and tumor cellularity in a rat model of cerebral glioma at 7 T. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 2013 doi: 10.1002/mrm.24873. Epub 2013/07/24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cha S, Yang L, Johnson G, Lai A, Chen M-H, Tihan T, et al. Comparison of microvascular permeability measurements, Ktrans, determined with conventional steady-state T1-weighted and first-pass T2*-weighted MR imaging methods in gliomas and meningiomas. American journal of neuroradiology. 2006;27(2):409–17. [PMC free article] [PubMed] [Google Scholar]
- 19.Brown SL, Nagaraja TN, Aryal MP, Panda S, Cabral G, Keenan KA, et al. MRI-Tracked Tumor Vascular Changes in the Hours after Single-Fraction Irradiation. Epub before publication. Radiation research. 2015 doi: 10.1667/RR13458.1. Epub 2015/05/27. [DOI] [PubMed] [Google Scholar]
- 20.Nagaraja TN, Aryal MP, Brown SL, Bagher-Ebadian H, Mikkelsen T, Yang JJ, et al. Cilengitide-induced temporal variations in transvascular transfer parameters of tumor vasculature in a rat glioma model: identifying potential MRI biomarkers of acute effects. PLoS One. 2013;8(12):e84493. doi: 10.1371/journal.pone.0084493. Epub 2014/01/01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Elmghirbi R, Nagaraja TN, Brown SL, Panda S, Aryal MP, Keenan KA, et al. Acute Temporal Changes of MRI-Tracked Tumor Vascular Parameters after Combined Anti-angiogenic and Radiation Treatments in a Rat Glioma Model: Identifying Signatures of Synergism. Radiation research. 2016 doi: 10.1667/RR14358.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Brown SL, Nagaraja TN, Aryal MP, Panda S, Cabral G, Keenan KA, et al. MRI-Tracked Tumor Vascular Changes in the Hours after Single-Fraction Irradiation. Radiat Res. 2015;183(6):713–21. doi: 10.1667/RR13458.1. [DOI] [PubMed] [Google Scholar]
- 23.Ewing JR, Wei L, Knight RA, Pawa S, Nagaraja TN, Brusca T, et al. Direct comparison of local cerebral blood flow rates measured by MRI arterial spin-tagging and quantitative autoradiography in a rat model of experimental cerebral ischemia. J Cereb Blood Flow Metab. 2003;23(2):198–209. doi: 10.1097/01.WCB.0000046147.31247.E8. [DOI] [PubMed] [Google Scholar]
- 24.Patlak C, Blasberg R. Graphical Evaluation of blood to brain transfer constants from multiple time up take data. Generalizations. J Cereb Blood Flow Metab. 1985;5:584–90. doi: 10.1038/jcbfm.1985.87. [DOI] [PubMed] [Google Scholar]
- 25.Patlak CS, Blasberg RG, Fenstermacher JD. Graphical evaluation of blood-to-brain transfer constants from multiple-time uptake data. J Cereb Blood Flow Metab. 1983;3:1–7. doi: 10.1038/jcbfm.1983.1. [DOI] [PubMed] [Google Scholar]
- 26.Logan J, Fowler JS, Volkow ND, Wolf AP, Dewey SL, Schlyer DJ, et al. Graphical analysis of reversible radioligand binding from time-activity measurements applied to [N-11C-methyl]-(−)-cocaine PET studies in human subjects. J Cereb Blood Flow Metab. 1990;10(5):740–7. doi: 10.1038/jcbfm.1990.127. [DOI] [PubMed] [Google Scholar]
- 27.Ewing JR, Nagaraja TN, Aryal MP, Keenan KA, Elmghirbi R, Bagher-Ebadian H, et al. Peritumoral tissue compression is predictive of exudate flux in a rat model of cerebral tumor: an MRI study in an embedded tumor. NMR Biomed. 2015 doi: 10.1002/nbm.3418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Boucher Y, Baxter LT, Jain RK. Interstitial pressure gradients in tissue-isolated and subcutaneous tumors: implications for therapy. Cancer Res. 1990;50(15):4478–84. Epub 1990/08/01. [PubMed] [Google Scholar]
- 29.Baxter LT, Jain RK. Transport of fluid and macromolecules in tumors. I. Role of interstitial pressure and convection. Microvasc Res. 1989;37(1):77–104. doi: 10.1016/0026-2862(89)90074-5. [DOI] [PubMed] [Google Scholar]
- 30.Liu LJ, Brown SL, Ewing JR, Schlesinger M. Phenomenological model of interstitial fluid pressure in a solid tumor. Physics Review E. 2011;84(2):021919-1–9. doi: 10.1103/PhysRevE.84.021919. Epub 15 Aug 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Yao W, Li Y, Ding G. Interstitial fluid flow: the mechanical environment of cells and foundation of meridians. Evidence-Based Complementary and Alternative Medicine. 2012;2012 doi: 10.1155/2012/853516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Bear J. Dynamics of fluids in porous media. Elsevier; NewYork: 1972. [Google Scholar]
- 33.Netti PA, Berk DA, Swartz MA, Grodzinsky AJ, Jain RK. Role of extracellular matrix assembly in interstitial transport in solid tumors. Cancer Res. 2000;60(9):2497–503. Epub 2000/05/16. [PubMed] [Google Scholar]
- 34.Pishko GL, Astary GW, Mareci TH, Sarntinoranont M. Sensitivity analysis of an image-based solid tumor computational model with heterogeneous vasculature and porosity. Ann Biomed Eng. 2011;39(9):2360–73. doi: 10.1007/s10439-011-0349-7. Epub 2011/07/14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Maindonald J, Braun AJ. Data Analysis and Graphics Using R. In: Ghahramani Z, Gill R, Kelly FP, Ripley BD, Ross S, Silverman BW, et al., editors. An Example-Based Approach. 3. Cambridge, U.K: Cambridge University Press; 2010. [Google Scholar]
- 36.R_Core_Team. R: A language and environment for statistical computing. 2013 Available from: http://www.R-project.org/
- 37.Rofstad EK, Tunheim SH, Mathiesen B, Graff BA, Halsor EF, Nilsen K, et al. Pulmonary and lymph node metastasis is associated with primary tumor interstitial fluid pressure in human melanoma xenografts. Cancer Res. 2002;62(3):661–4. Epub 2002/02/07. [PubMed] [Google Scholar]
- 38.Boucher Y, Brekken C, Netti P, Baxter L, Jain R. Intratumoral infusion of fluid: estimation of hydraulic conductivity and implications for the delivery of therapeutic agents. British journal of cancer. 1998;78(11):1442. doi: 10.1038/bjc.1998.705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Milosevic M, Lunt SJ, Leung E, Skliarenko J, Shaw P, Fyles A, et al. Interstitial permeability and elasticity in human cervix cancer. Microvasc Res. 2008;75(3):381–90. doi: 10.1016/j.mvr.2007.11.003. Epub 2008/01/12. [DOI] [PubMed] [Google Scholar]
- 40.Levick J. Flow through interstitium and other fibrous matrices. Quarterly journal of experimental physiology. 1987;72(4):409–37. doi: 10.1113/expphysiol.1987.sp003085. [DOI] [PubMed] [Google Scholar]
- 41.Swabb EA, Wei J, Gullino PM. Diffusion and convection in normal and neoplastic tissues. Cancer Res. 1974;34(10):2814–22. [PubMed] [Google Scholar]
- 42.DiResta GR, Lee J, Larson SM, Arbit E. Characterization of neuroblastoma xenograft in rat flank. I. Growth, interstitial fluid pressure, and interstitial fluid velocity distribution profiles. Microvascular research. 1993;46(2):158–77. doi: 10.1006/mvre.1993.1044. [DOI] [PubMed] [Google Scholar]
- 43.Ewing JR, Jiang Q, Boska M, Zhang ZG, Brown SL, Li GH, et al. T1 and magnetization transfer at 7 Tesla in acute ischemic infarct in the rat. Magn Reson Med. 1999;41(4):696–705. doi: 10.1002/(sici)1522-2594(199904)41:4<696::aid-mrm7>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.