High resolution whole brain diffusion MRI at 7 Tesla using radiofrequency parallel transmission

Abstract

Purpose

Investigating the utility of RF parallel transmission (pTx) for Human Connectome Project (HCP)-style whole-brain diffusion MRI (dMRI) data at 7 Tesla (7T).

Methods

Healthy subjects were scanned in pTx and single-transmit (1Tx) modes. Multiband (MB), single-spoke pTx pulses were designed to image sagittal slices. HCP-style dMRI data (i.e., 1.05-mm resolutions, MB2, b-values=1000/2000 s/mm², 286 images and 40-minute scan) and data with higher accelerations (MB3 and MB4) were acquired with pTx.

Results

pTx significantly improved flip-angle detected signal uniformity across the brain, yielding ~19% increase in temporal signal-to-noise ratio (tSNR) averaged over the brain relative to 1Tx. This allowed significantly enhanced estimation of multiple fiber orientations (with ~21% decrease in dispersion) in HCP-style 7T dMRI datasets. Additionally, pTx pulses achieved substantially lower power deposition, permitting higher accelerations, enabling collection of the same data in 2/3 and 1/2 the scan time or of more data in the same scan time.

Conclusion

pTx provides a solution to two major limitations for slice-accelerated high-resolution whole-brain dMRI at 7T; it improves flip-angle uniformity, and enables higher slice acceleration relative to current state-of-the-art. As such, pTx provides significant advantages for rapid acquisition of high-quality, high-resolution truly whole brain dMRI data.

Introduction

The Human Connectome Project (HCP, http://humanconnectome.org) initiative of the National Institutes of Health (NIH) has led to the development of broadly useful, extensively tested and optimized MRI acquisition protocols, and a collection of high-quality, freely shared magnetic resonance based neuroimaging data (1–3) at both 3 and 7 Tesla (3T and 7T, respectively). The diffusion imaging (dMRI) component of this effort at 7T was obtained with a higher spatial resolution (~2-fold smaller voxel volume) and was demonstrated to possess some advantages over the 3T dMRI data in inferring brain connectivity, despite using lower b-values and sampling fewer q-space points (4,5). However, the 7T HCP acquisition was compromised by two RF related challenges: namely, the flip-angle nonuniformity over the brain and power deposition (i.e. Specific Absorption Rate or SAR). With a single-channel transmit head coil operated in the Circularly Polarized (CP) mode, transmit B₁ (B₁⁺) magnitude in the human brain is highly inhomogeneous at 7T, exhibiting low values in the periphery (6,7) as well as in the cerebellum and inferior temporal lobes (e.g. (8) and references therein). Especially with techniques that require 180° pulses (such as dMRI), this results in spatially non-uniform signal magnitude and signal-to-noise ratio (SNR) in the image, even displaying signal dropouts in regions where the B₁⁺ is particularly weak. In the HCP, the RF inhomogeneity problem at 7T was partially mitigated by the use of passive RF shimming with dielectric padding (4,9); although this increased image signals in lower brain regions, it did not uniformly improve the flip angles across the brain, leading to the same undesired variations of image contrast and SNR.

It is also well recognized that slice acceleration using multiband (MB) pulses, a critical approach employed in the HCP and contemporary dMRI acquisitions in general, leads to SAR increases by the number of simultaneously excited slices, (i.e. the Multiband (MB) factor) when the acceleration is used to reduce the image repetition time (TR). This SAR increase can be mitigated by lowering the time bandwidth product (TBWP) of the pulses employed (10–13), albeit at the expense of increased sensitivity to off-resonance effects and consequent undesirable distortions in slice definition. Such a TBWP compromise was not employed in the HCP because of the presence of large B₀ inhomogeneities in the human brain at 7T. Consequently, the 7T HCP dMRI acquisition was limited to a slice acceleration of 2 because of SAR limitations.

It is possible to simultaneously tackle the two challenges of SAR and RF non-uniformity for MB accelerated imaging using RF parallel transmission (pTx). Recognizing this (14), we introduced a general formalism for pTx MB pulse design that significantly improved B₁⁺ homogeneity in the human brain at 7T while substantially reducing the RF power requirement compared to a CP-like mode that mimicked a single transmit application in the same RF coil (15). Poser et al. (16) also reported similar results at 3T when acquiring MB accelerated simultaneous multislice (SMS) brain images with a gradient echo EPI sequence. Subsequently, towards achieving whole brain coverage, we introduced a generalized slab-wise pTx design framework (17) and demonstrated its utility for 7T whole-brain dMRI (18).

Here, we report advances towards using pTx to achieve high-quality, high-resolution, and high-efficiency whole-brain dMRI at 7T. Particularly, we demonstrate the utility of pTx in the context of a 7T HCP-style whole brain acquisition (i.e., an acquisition similar to that of the HCP 7T dMRI protocol, obtaining whole-brain slice-accelerated data with ~1-mm isotropic resolution, multi-shell q-space sampling and a total of ~40-minute scan time). In these studies, we utilized the commercially available Nova 8-channel transmit and 32-channel receive (Nova 8Tx32Rx) head coil (Nova Medical, Inc., MA, USA). More optimal transmit coil geometries exist for SAR reduction and/or B₁⁺ homogenization (19–22); however, Nova 8Tx32Rx permits a direct comparison to the HCP data because it shares the same 32-channel receiver as the Nova 1Tx32Rx coil employed in the HCP. Our results show that pTx can significantly improve flip-angle uniformity across the entire brain while simultaneously reducing SAR compared to a single-transmit configuration (i.e., Nova 1Tx32Rx coil) as employed in the 7T HCP protocol.

Methods

Human studies were conducted on a 7T scanner (Siemens, Erlangen, Germany) with 32 receive-channels, which can operate in a single-transmit (1Tx) or pTx mode. The latter has 16 independent transmit channels with a 1-kW RF power amplifier per channel; only 8 of these channels were employed in this study. The 1Tx mode used a combined 8-kW RF amplifier.

Human brain images were collected in healthy subjects who signed a consent form approved by the local Institutional Review Board. Each subject was scanned first in the pTx mode using the Nova 8Tx32Rx head coil and then in the 1Tx mode using the Nova 1Tx32Rx head coil. To ensure RF safety, the Nova 8Tx32Rx coil was used in the “protected” mode in which total RF power delivery (measured as sum of forward minus reflected power across all of the 8 transmit channels in use) was monitored on the fly to be within the power limits specified by the coil manufacturer. In this study, the power limits were set to 11 W for long-term (6 minutes) and 22 W for short-term (10 seconds) RF exposures. For the 1Tx acquisition, dielectric padding was employed in the Nova 1Tx32Rx coil, as in the 7T HCP dMRI protocol, to improve the B₁⁺ field in lower brain regions.

Band-specific pTx multiband pulse design

Band-specific pTx MB pulses were designed with single spokes (corresponding to RF phase and amplitude shimming) following the slab-wise design framework (17) where band-specific RF shim values (i.e. RF amplitude and phase modulations) were calculated based on a small number of contiguous slabs. In this design, although each “single band” pTx pulse component of the pTx MB pulse is a single spoke, the final composite pTx MB pulses are composed of multiple, single band pulses with band-specific optimization; as such, pTx MB pulses require channel-specific waveforms (20). Furthermore, pTx MB pulses were designed to image sagittal slices in order to maximally exploit the transmit coil geometry for RF performance (20). Calculation of RF shim sets for pTx pulses was performed in MATLAB (The Mathworks Inc., Natick, MA, USA).

Multichannel multislice B₁⁺ maps were obtained in 24 contiguous sagittal slabs (each 6.3 mm in thickness) spanning 151.2 mm in the left-right dimension. For each slab, a single set of 8-channel B₁⁺ maps were measured using a hybrid B₁⁺ mapping technique which provides accurate B₁⁺ maps for pTx methods at 7T and beyond (23). Briefly this method combines a single absolute B₁⁺ map (obtained in the large tip angle regime by transmitting with all channels) together with a series of relative B₁⁺ maps obtained in the small tip angle regime by transmitting one channel at a time. In this study, the absolute B₁⁺ map was obtained using the actual flip angle imaging (AFI) (24) and the phase configuration obtained by a CP-like mode RF phase shimming procedure (25) to avoid any B₁⁺ dropout across the entire brain. The series of relative B₁⁺ maps was acquired using a multislice gradient recalled echo sequence. Detailed imaging parameters utilized for B₁⁺ mapping can be found in the Supporting information.

For each B₁⁺ mapping slab, a single set of 8-channel RF shim values were found, leading to a total of 24 RF shim sets. All RF shim sets were optimized jointly by solving the following minimization problem:

$${\text{min}}_{\mathrm{w}}{\Vert \left|\text{Aw}\right|-1\Vert }_2^2+\mathrm{\lambda }{\Vert \mathrm{w}\Vert }^2$$ [1]

where w is a complex-valued vector concatenating all of the 8×24 RF shim values (corresponding to 8 transmit channels and 24 B₁⁺ mapping slabs), A is the complex-valued system matrix constructed to be block diagonal (17) and involving the B₁⁺ maps within the region of interest (ROI), “1” represents a uniform B₁⁺ field across the ROI, and λ is the regularization parameter. The design problem in Eq. [1] was solved based on the MATLAB function “fminunc”.

To increase the robustness and reduce the chance of being trapped by undesired local minima, the design problem in Eq. [1] was solved in two steps. The first step was to find a good initial point of the entire set of RF shim values. This was done by decomposing the design problem into 24 sub-design problems, each corresponding to RF shimming for one B₁⁺ mapping slab. These sub-problems were solved one at a time in a sequential manner. For each sub-problem, 20 randomly created initial points were utilized to obtain 20 solutions among which the one that gave rise to the least cost function value was chosen as the optimum solution. The resulting 24 optimum slab-specific solutions were used to form the good initial point. Starting from this initial point, the second step was to further optimize all of the RF shim values in a joint manner. For both steps, a constant regularization parameter determined by the L-curve criterion (26) was utilized.

The calculation of pTx RF shim values described above only targeted an ROI of brain tissues. To define this ROI, a brain mask was created by acquiring a 0.7-mm, T1-weighted whole head image (see Supporting information) and applying the FSL brain extraction tool (27) to extract the entire brain including cerebrum, midbrain and cerebellum.

pTx-enabled multiband dMRI pulse sequence

In line with the slab-wise pTx MB pulse design framework, a new pTx-enabled MB dMRI pulse sequence was developed to enable the application of multiple pTx RF pulses for excitation and refocusing. It was an upgrade to an older version of our pTx MB sequence that could only support application of a single pTx MB pulse (18). Like the sequence used in the HCP, the new sequence was built to integrate single-band (SB) reference scans, allow in-plane acceleration, and enable fast online image reconstruction. It can also load in band and channel-specific RF shim values stored in a text file to form pTx SB pulses for SB reference scans and to form pTx MB pulses for image acquisition. It also allowed pulse-type specific RF shim values to be used for RF excitation and refocusing. When in-plane acceleration is turned on, the sequence allows auto-calibration scans to be performed using an integrative gradient echo sequence from which the pTx RF excitation pulse is created with the same RF shim values as specified for RF excitation in the subsequent dMRI acquisition.

As in the 7T HCP dMRI acquisition (4), the studies presented here also employed time-shifted MB pulses (28) to reduce the peak RF power, and more importantly the online SAR overestimation which would have otherwise required a longer TR to be utilized (4).

Comparing different transmit configurations using 2-fold slice acceleration acquisitions

We first performed a pilot study by scanning a single subject and comparing three transmit configurations: 1) pTx mode using the Nova 8Tx32Rx head RF coil and pTx MB pulses, 2) 1Tx mode using the Nova 1Tx32Rx coil with conventional MB pulses and 3) 1Tx mode using the Nova 1Tx32Rx with dielectric padding and conventional MB pulses.

With each transmit configuration, we initially acquired whole-brain dMRI data with 1.05-mm isotropic¹ resolution and MB2 as in the original 7T HCP dMRI protocol (4), but using only single-shell, b=1500 s/mm², q-space sampling for simplicity (as opposed to 2 shells with b=1000, and 2000 s/mm² in the original HCP). These pilot datasets consisted of a total of 73 image volumes, 65 diffusion weighted with b=1500 s/mm² plus 8 interspersed b=0 volumes. To allow for correction of EPI geometric distortions in the subsequent data analysis, another set of six b=0 images were also acquired with matched imaging parameters but inverted phase encoding direction (see Supporting information for more details).

Demonstrating the utility of pTx by acquiring full HCP dMRI data

To demonstrate more comprehensively the utility of pTx for high-resolution dMRI at 7T, we scanned five subjects (18–65 years of age, 2 males, 3 females) and acquired full HCP-style dMRI data using pTx MB pulses (defined here as the HCP pTx protocol) and with the original HCP 7T protocol (defined here as the HCP 1Tx protocol) (4). In both cases, whole brain was covered with 1.05 mm isotropic resolution, iPAT3 (3-fold in-plane acceleration), two-fold slice acceleration (MB2), two shell q-space sampling (b=1000 and 2000 s/mm²) (see Supporting information for other relevant imaging parameters). The HCP 1Tx protocol employed the Nova 1Tx/32 channel coil, dielectric padding, and the same oblique-axial slices of the original HCP data (4). The HCP pTx protocol used pTx MB2 pulses and sagittal slices (instead of oblique axial slices), requiring more slices (144 vs. 132) to cover the whole brain in the left-right dimension and resulting in a slightly increased TR (7400 vs. 7000 ms).

Exploring higher slice accelerations enabled by pTx

When using pTx MB pulses to acquire full HCP dMRI data with MB2, the online readings for the long-term 6-minute total RF power were ~40% of the prescribed limit, suggesting that higher slice accelerations (e.g. MB3 or MB4) would be possible with our pTx MB pulses. Accordingly, we acquired dMRI data with the HCP pTx protocol but using pTx MB3 pulses from the same five subjects; this acquisition (pTx MB3 protocol) employed the same HCP pTx parameters except it achieved a shorter TR (4934 vs. 7400 ms for MB2) and used a tailored inter-slice shift (1/4 FOV instead of ½ FOV) to minimize g-factor noise penalties. A reduced inter-pulse time shift (960 vs. 1920 μs for MB2) between single-band RF pulses was imposed to retain the echo time of 71 ms.

Increased acceleration with the pTx MB3 pulses was employed to acquire additional diffusion directions while keeping the total acquisition time the same as in the HCP pTx protocol. Two-shell q-space sampling (b-values=1000, 2000 s/mm² as in the HCP) was retained but with increased image volumes, corresponding to 95 unique diffusion directions per shell and 22 interspersed b=0 images, acquired twice with AP and PA phase encode directions. Like the HCP protocol, the total acquisition was split into 4 segments of ~10 minutes each.

Feasibility of further slice acceleration was also examined in two subjects using pTx MB4 pulses, even though, on the receive side, unaliasing 12-fold accelerated (4-fold-slice and 3-fold in-plane) images with the 32-channel array is expected to lead to increased g-factor noise and, as such, degradation of the performance in many diffusion imaging metrics. This protocol, defined as the pTx MB4 protocol, was the same as the HCP pTx protocol, except that a further reduced TR (3701 vs. 7400 ms for MB2) and a tailored inter-slice shift (1/4 FOV instead of ½ FOV) were utilized. The inter-pulse time shift between single-band RF pulses was further reduced to 640 μs to retain the echo time of 71 ms. As in the pTx MB3 acquisition, the total acquisition time was kept constant and dMRI data with increased diffusion directions were acquired, using the same two-shell q-space sampling (b-values=1000 and 2000 s/mm²). A total of 574 image volumes were obtained, corresponding to 129 unique diffusion directions per shell and 29 interspersed b=0 images, acquired twice with AP and PA phase encode directions.

Table 1 summarizes relevant imaging parameters for the dMRI protocols utilized in this study. A flowchart (Fig. 1) illustrates the workflow involved in the dMRI acquisition with pTx.

Table 1.

Relevant imaging parameters for the dMRI protocols investigated in the current study

	TR (ms)	MB factor	b values (s/mm2)	# of diffusion directions/shell	# of b0 images	# of slices	Slice orient	inter-slice shift (FOV)	time shift (us)
Pilot study	7400	2	1500	65	8	144	Sagittal	1/2	1920
HCP 1Tx	7000	2	1000/2000	64	15	132	Oblique axial	1/2	1920
HCP pTx	7400	2	1000/2000	64	15	144	Sagittal	1/2	1920
pTx MB3	4934	3	1000/2000	95	22	144	Sagittal	1/4	960
pTx MB4	3701	4	1000/2000	129	29	144	Sagittal	1/4	640

Other relevant imaging parameters that were kept constant for all protocols listed include 1.05 mm isotropic resolution, 71 ms echo time, 3-fold in-plane acceleration (iPAT3), 6/8 partial Fourier, 210(RO)×210(PE) mm² field of view, 0.82 ms echo spacing, and 1388 Hz/pixel bandwidth. For all of the HCP and pTx related acquisitions, the listed diffusion weighted and b0 images were acquired twice with inverted phase encode directions (ie Anterior-Posterior (AP) and PA) and the total acquisition was divided into 4 segments of ~10 minutes each. For the pilot study, the listed diffusion weighted and b0 images were acquired once with the AP phase encode direction, and another set of six b0 images were acquired with matched imaging parameters but with the PA phase encode direction.

Fig. 1.

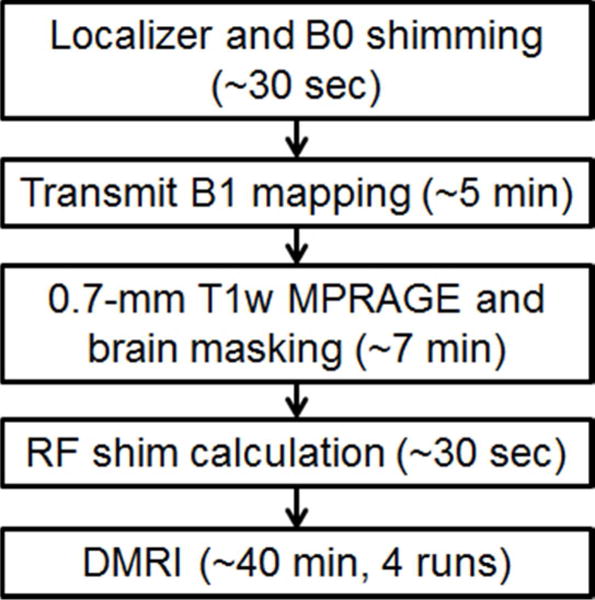
A flowchart summarizing the procedures involved in the dMRI data acquisitions using parallel transmission. The time spent on preparing RF shim values before data acquisition was about 13 minutes, including 5 minutes of transmit B₁ mapping and 7 minutes of T1w imaging and brain masking. The total data acquisition was 40 minutes, divided into 4 runs of about 10 minutes each. For each run, reference scans for in-plane and slice GRAPPA took about 1–2 minutes.

For pTx MB3 and MB4 acquisitions, the q-space sampling scheme was designed using the same algorithm (29) as in the HCP 7T dMRI protocol to ensure not only uniform angular coverage across the q-space, but also comparable sampling density across the two shells (i.e., with more points sampled on the outer shell). Furthermore, it was constructed incrementally to be compatible with prematurely aborted scans, i.e., a termination at any point of acquisition would have an approximately optimal design. Additionally, it interspersed b=0 images as in the HCP 7T dMRI protocol (i.e., it inserted a b=0 image after every 9^th diffusion-weighted image). Consequently, the q-space sampling scheme utilized for the MB4 data acquisition encompassed those of the MB2 and MB3 acquisitions, meaning that terminating the MB4 data acquisition halfway or at 3/4 of the scan would have resulted in the same q-space sampling as in the MB2 or MB3 acquisition. To demonstrate the usefulness of the MB4 acquisition, we mimicked a 20-minute scan by only analyzing the first half of the entire acquisition (i.e., the first 286 image volumes) and compared the result with that of the HCP 1Tx protocol (which also acquired 286 image volumes using identical q-space sampling).

dMRI data preprocessing and analysis

We followed the FSL pipeline (30) to preprocess the dMRI data for our pilot study, and the HCP preprocessing pipeline (31) for all of the subsequent HCP-style acquisitions. In each case, the dMRI data were corrected for head motion as well as geometric EPI distortions arising from susceptibility and eddy currents. This was achieved by combining the FSL “topup” (32) and “eddy” (33) routines. In our pilot study, the preprocessed single-shell dMRI data were used to fit a diffusion tensor model to derive such metrics as fractional anisotropy (FA), direction of the principle eigenvector and sum of squared errors (SSE) of the fitting.

For comparison of the HCP pTx protocol vs. the HCP 1Tx protocol, the preprocessed double-shell dMRI data were first evaluated by calculating temporal SNR (tSNR) (34). For each protocol, a tSNR map was calculated on a voxel-wise basis from the 15 b0 images at the individual subject level, treating these b0 images as a time-series; the tSNR was quantified at the whole brain level by averaging across the entire masked brain. The preprocessed dMRI data were then used to fit an advanced diffusion model (35) to estimate multiple fiber orientations, including such metrics as the orientation, orientation uncertainty and volume fraction for the principal, the second and the third fibers. Similar data analysis was performed to evaluate the data acquisition with pTx MB3 and MB4 protocols.

Results

Comparing different transmit configurations in a single subject

The use of pTx significantly improved RF uniformity across the entire brain as compared to the 1Tx acquisition (Supporting Fig. S1), with the coefficient of variation (i.e., std/mean) of the RF distribution reduced by over 50% (std/mean=~10% for pTx vs. ~22% for 1Tx counterparts).

The use of 1Tx alone yielded regionally lower signal intensity and signal dropouts in the brain, especially in the cerebellum and inferior temporal lobes (Fig. 2); this translated into noisy depictions of principle fiber orientations in these regions (Fig. 3a). Although recovering the cerebellum, adding dielectric padding did not restore the inferior temporal lobe; it even led to degradation in other regions observed as patches of increased SSE (Sum of Squares Error) values in fiber depiction (Fig. 3b, sagittal and axial slice, middle row). In contrast, the use of pTx effectively improved fiber depiction in both cerebellum and inferior temporal lobe; furthermore, it largely enhanced accuracy for tensor model fitting, with the whole-brain average SSE reduced by up to 24% relative to the single-transmit cases.

Fig. 2.

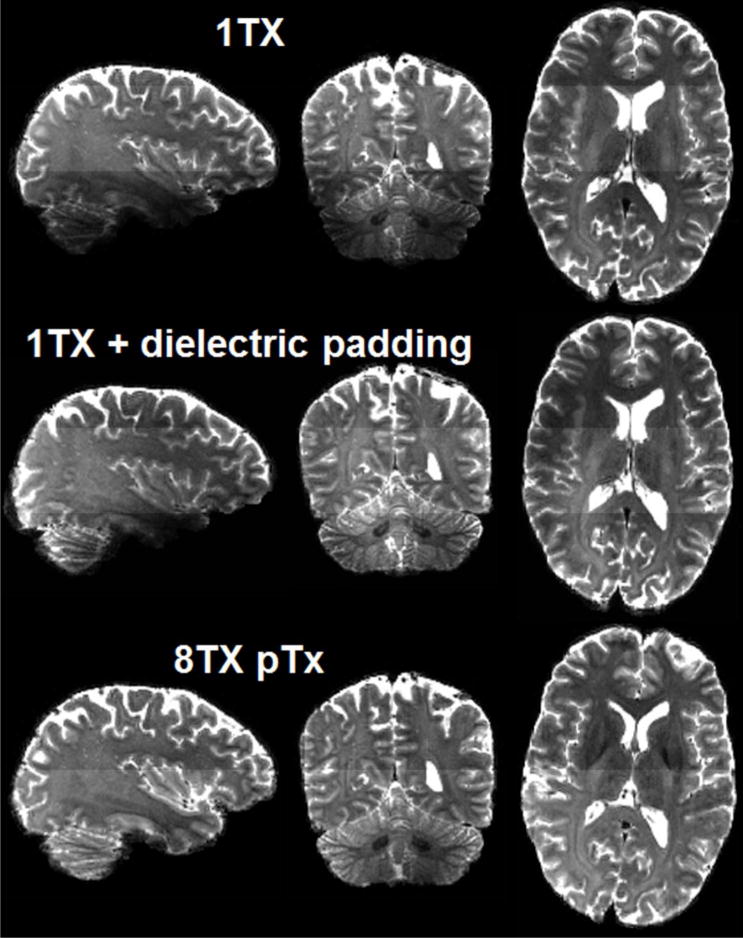
Comparing Nova single transmit (1Tx) coil alone (top row) and with dielectric padding (middle row), Nova 8Tx coil with pTx (bottom row) when acquiring high resolution whole brain dMRI at 7T with MB2. Shown are b=0 images of dMRI data acquisition with inter-slice shift=FOV/2, in-plane acceleration factor=3, TR/TE=7400/71 ms, acquisition time=10 min. For distortion correction, six b=0 images were acquired with same imaging parameters but inverted phase encode direction. Note that although the use of dielectric padding restored tissue contrast in the cerebellum, it did not do so in lower temporal lobe; by contrast, the use of pTx recovered tissue contrast in both regions.

Fig. 3.

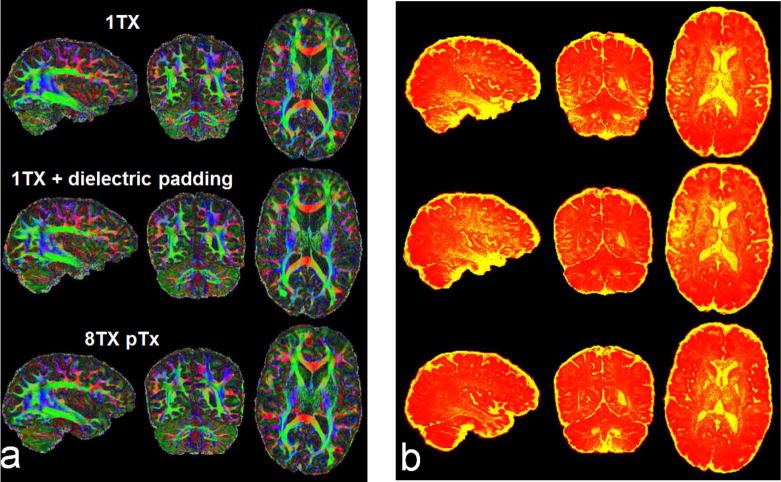
Comparing Nova single transmit (1Tx) coil alone (top row) and with dielectric padding (middle row), Nova 8Tx coil with pTx (bottom row) when acquiring high resolution whole brain dMRI at 7T with MB2. Shown are color fractional anisotropy (FA) maps (a) and corresponding sum of squared error (SSE) maps (b), derived by fitting a tensor model to the single-shell dMRI data acquired with inter-slice shift=FOV/2, in-plane acceleration factor=3 (iPAT3), TR/TE=7400/71 ms, acquisition time=10 min. For distortion correction, six b=0 images were acquired with same imaging parameters but inverted phase encode direction. The color FA is FA (in the range of [0 1]) with the color representing the orientation of the first eigenvector (red: left-right; green: anterior-posterior; blue: inferior-superior). The SSE map is shown in a colorscale of [0 12] (with yellow being high and red being low in SSE). Note that the use of pTx led to clear depiction of fibers not only in the cerebellum but also in the lower temporal lobe, and quantitatively, it reduced the whole brain average (excluding CSF) SSE by 22% relative to the combinational use of dielectric padding and Nova 1Tx coil, and by 24% relative to the use of Nova 1Tx coil alone.

Demonstrating the utility of pTx in five subjects by acquiring full HCP dMRI data

The use of the HCP pTx protocol enhanced tSNR (as measured from the multiple b=0 images obtained during the dMRI acquisition) relative to the HCP 1Tx acquisition (Fig. 4). Quantitative analysis based on a one-tailed paired t-test revealed that the whole brain average tSNR was elevated by ~19% (p=0.0004, T(4)). Additionally, tSNR on average was increased in 63% of voxels covering the brain volume. The histograms of tSNR at the subject level are also reported in Supporting Fig. S2 for comparing HCP 1Tx vs HCP pTx protocols.

Fig. 4.

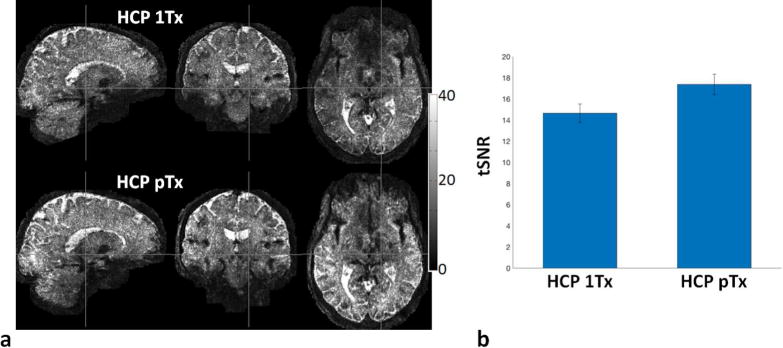
Evaluation of temporal signal-to-noise ratio (tSNR) for the HCP 1Tx (the original HCP 7T protocol) vs the HCP pTx protocols. (a) tSNR maps in one subject. (b) Whole brain tSNR averaged across five subjects, with the error bars being the standard deviation. For each subject, the tSNR map was calculated on a voxel-wise basis from the 15, minimally preprocessed, b0 images of each HCP 1Tx and HCP pTx dataset, and the tSNR per dataset was quantified at the whole brain level by averaging across the entire masked brain. Note that the use of pTx nearly increased the tSNR across the entire brain with the tSNR on average increased by 19% (p=0.0004, T(4)).

Furthermore, the use of the HCP pTx protocol improved the estimation of fractional anisotropy and fiber crossings (shown for one subject in Fig. 5). While providing comparable high image quality across the brain, it led to clearer depiction of principal fiber orientations in the lower temporal lobe (Fig. 5a). More evidently, it resulted in largely improved estimation of second fiber orientations observed not only in the temporal lobe but also in the cerebellum (Fig. 5b). Similar results from another subject are illustrated in Supporting Fig. S3.

Fig. 5.

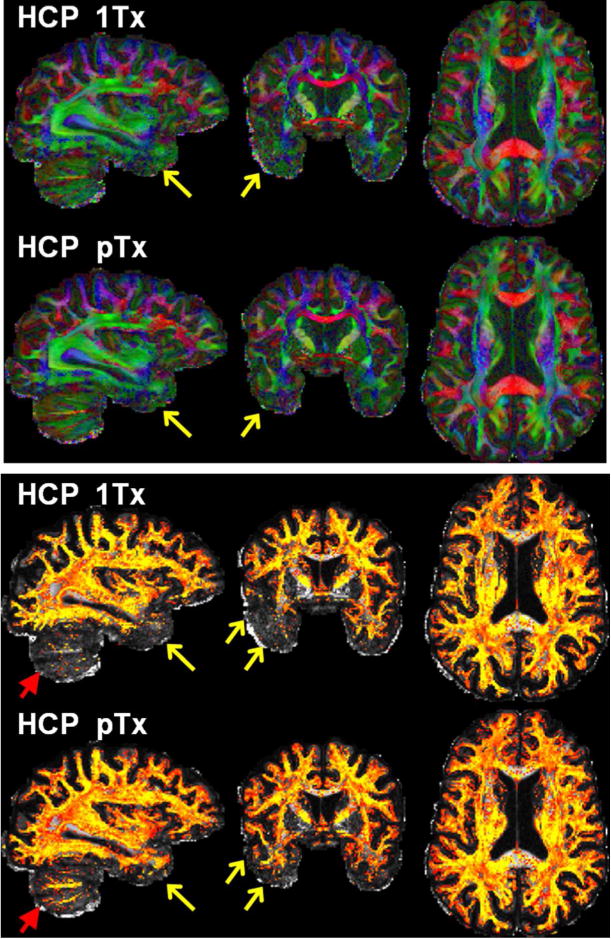
Comparing HCP 7T dMRI protocol (HCP 1Tx) with HCP pTx protocol. Data are shown for one subject. Shown are color fractional anisotropy (FA) maps (top panel) and volume fraction maps for second fiber orientations (bottom panel). The color FA is FA (in the range of [0 1]) with the color representing the orientation of the principal fiber (red: left-right; green: anterior-posterior; blue: inferior-superior). The volume fraction map is shown in a colorscale of [0.05 0.2] (with yellow being high and red being low in volume fraction), overlaid on the respective FA map (in a grayscale of [0 1]). Both dMRI datasets were acquired with 1.05 mm isotropic resolutions, MB2, in-plane acceleration factor=3, and TE=71 ms. The TR for pTx acquisition was slightly longer (7400 vs 7000 ms). Both acquisitions utilized the same q-space sampling scheme (double shells, b-value=1000/2000 s/mm2), corresponding to 143 unique image volumes, each acquired twice with anterior-posterior (AP) and PA phase encode directions. Total scan time was kept constant for both datasets (i.e., 40 minutes divided into 4 segments of 10 minutes each). Note that the use of pTx improved fiber orientation estimation performances not only in lower temporal lobe (as indicated by yellow arrows) but also in cerebellum (as highlighted by red arrows).

Quantitatively, the use of the HCP pTx protocol in five subjects substantially and significantly decreased dispersion for all of the three fiber orientations (Fig. 6a), with the decrease on average being ~21% for the principal (p=3e-4, T(4)), ~11% for the second (p=1e-4, T(4)), and ~19% for the third (p=2e-4, T(4)) fiber orientation estimations. While slightly decreasing (by <1%) the percent volume (relative to the volume of whole brain) for principal fiber orientation (p=0.11, T(4)), the use of the HCP pTx protocol increased the percent volume for both second and third fiber orientations (Fig. 6b), with the increase on average being ~13% (p=5e-4, T(4)) for the second and ~44% (p=1e-5, T(4)) for the third fiber orientations.

Fig. 6.

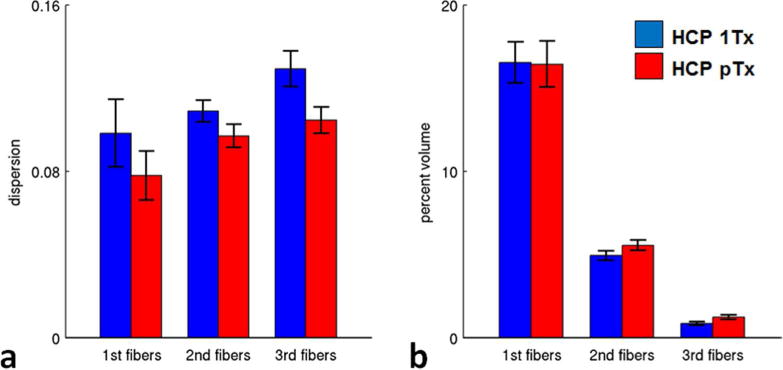
Fiber orientation estimation performance of HCP 7T dMRI protocol (HCP 1Tx) vs the HCP pTx protocol (HCP pTx) (five subjects). The dispersion (a) was significantly decreased for all of the three fiber orientation estimations (i.e., principal (p=3e-4, T(4)), second (p=1e-4, T(4)) and third (p=2e-4, T(4)) fiber orientations). The percent volume (b) was slightly decreased (p=0.11, T(4)) for principal fiber orientations, but increased significantly for both second (p=5e-4, T(4)) and third (p=1e-5, T(4)) fiber orientations when using pTx pulses. Error bars are standard deviation across the same five subjects.

Exploring higher slice accelerations enabled by pTx

The use of the pTx MB3 protocol to acquire more data than the HCP pTx protocol yielded visually similar performance for estimation of principle and second fiber orientations (shown for one subject in Figs. 7 and 8, and another subject in Supporting Figs. S4 and S5). Quantitative analysis of five subjects revealed that on average it reduced the dispersion by ~5% (p=0.02, T(4)) and ~2% (p=0.03, T(4)) for principal and second fiber orientations, respectively; it also decreased the percent volume by ~5% (p=0.002, T(4)) and ~3% (p=0.034, T(4)) for principle and second fiber orientations, respectively. The use of the pTx MB3 protocol appeared to have little impact on estimation of third fiber orientation.

Fig. 7.

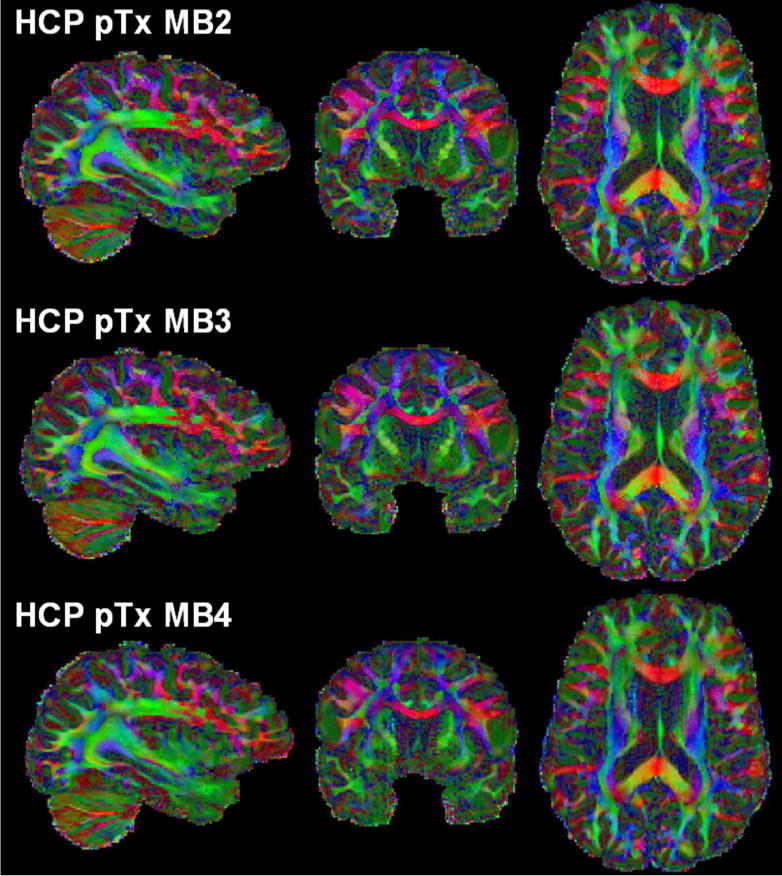
Color fractional anisotropy (FA) maps of the HCP pTx MB2 protocol (top row) vs the pTx MB3 protocol (middle row) vs the pTx MB4 protocol (bottom row) in one subject. The color FA is FA (in the range of [0 1]) with the color representing the orientation of the principal fiber (red: left-right; green: anterior-posterior; blue: inferior-superior). All three dMRI datasets were acquired with 1.05 mm isotropic resolutions, in-plane acceleration factor=3, TE=71 ms, and double-shell q-space sampling (b-value=1000/2000 s/mm2). Total scan time was kept constant for all acquisitions (i.e., ~40 minutes divided into 4 segments of 10 minutes each). Because of use of a shorter TR (3701 ms for MB4 and 4934 ms for MB3 vs 7400 ms for MB2), both MB3 and MB4 acquisitions obtained more data than the MB2 acquisition.

Fig. 8.

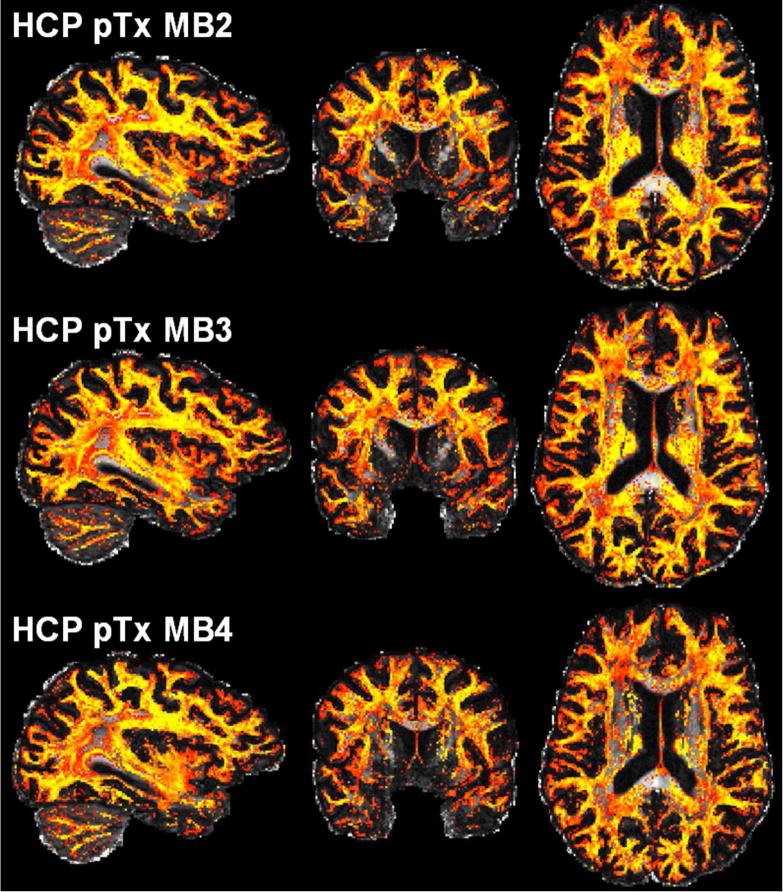
Volume fraction maps of second fiber estimation for the HCP pTx MB2 protocol (top row) vs the pTx MB3 protocol (middle row) vs the pTx MB4 protocol (bottom row) in one subject. These volume fraction maps, derived using the same data as in Fig. 7, are overlaid on the respective fractional anisotropy map (defined in the grayscale of [0 1]) and shown in a colorscale of [0.05 0.2] (with yellow being high and red being low in volume fraction).

When comparing the pTx protocols among themselves, the use of the pTx MB4 to further increase the data quantity (574 vs. 424 images for pTx MB3) for a constant scan time of ~40 minutes appeared to reduce the performances for estimation of multiple fiber orientations relative to the pTx MB protocol (Figs. 7 and 8, and Supporting Figs. S4 and S5). Quantitatively, the dispersion, averaged over two subjects, was increased by ~4% for the principle, ~12% for the second, and ~15% for the third fiber estimations, and the percent volume on average was decreased by ~5% for the principle, ~8% for the second, and ~20% for the third fiber estimations.

However, when sampled to mimic half the scan time and compared to the 40-minute HCP 1Tx protocol for the same number of q-space points on the same two b-shells, the pTx MB4 data still displayed improvements in the delineation of principle fiber orientations (Fig. 9a, arrow), and, more evidently, increased the percent volume of second fiber orientations in the lower temporal lobe (Fig. 9b, arrow). In the central regions, however, dropouts in the second fiber containing volumes was evident (axial slices, Fig. 9b), likely reflecting the increased g-factor noise due to excessive 4×3 two-dimensional acceleration for this coil.

Fig. 9.

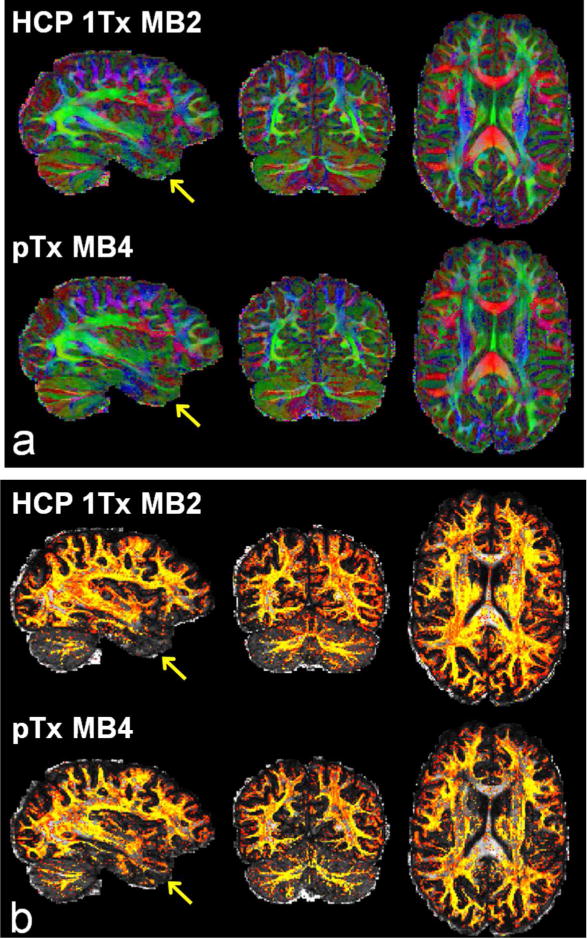
Comparing HCP 7T dMRI protocol with the pTx MB4 protocol in another subject. (a) Color fractional anisotropy (FA) maps. (b) Volume fraction maps for second fiber orientations. The color FA is FA (in the range of [0 1]) with the color representing the orientation of the principal fiber (red: left-right; green: anterior-posterior; blue: inferior-superior). The volume fraction map is shown in a colorscale of [0.05 0.2] (with yellow being high and red being low in volume fraction), overlaid on the respective FA map (in a grayscale of [0 1]). Both dMRI datasets were acquired with 1.05 mm isotropic resolutions, in-plane acceleration factor=3, TE=71 ms, and double-shell q-space sampling (b-value=1000/2000 s/mm2). Total number of image volumes was kept constant for both acquisitions (i.e., 286 images volumes were acquired as in the HCP 7T protocol). Because of use of a ~50% shorter TR (3701 vs 7400 ms for MB2), the MB4 acquisition would reduce the scan time by half (20 vs 40 minutes for MB2). Note that the use of pTx with MB4 to achieve the same data quantity in half scan time gave rise to better performances for estimation of multiple fiber orientations in lower brain regions especially the lower temporal lobe (as indicated by yellow arrows).

Discussion

We demonstrate here, for the first time, an HCP-style high-resolution whole-brain multiband-accelerated diffusion MRI at 7T using RF parallel transmission. Critical to this accomplishment is the development of a pTx-enabled single-shot 2D EPI spin echo sequence that can be used to acquire MB-accelerated dMRI data, as well as the use of the slab-wise pulse design framework (17) to increase time efficiency in B₁⁺ mapping, pulse design, and pulse sequence preparation. The results of our pilot study comparing pTx (using a Nova 8Tx32Rx coil) with two single-transmit counterparts (using Nova 1Tx32Rx coil with and without dielectric padding) indicate that pTx pulses improve flip-angle homogeneities, whereby enhancing SNR and contrast uniformity across the entire brain. Most notably, the use of pTx can effectively recover signal dropouts in both cerebellum and inferior temporal lobes (Fig.2), leading to a better depiction of principal fiber orientations in those challenging regions (Fig. 3).

Acquisition of full HCP dMRI datasets in five subjects further confirms the advantage of pTx over a single-transmit configuration and demonstrates that the use of pTx can significantly improve regional signal intensity and by implication SNR and spatial uniformity of SNR (Fig. 4), which in turn lead to better estimation of multiple fiber orientations (Figs. 5 and 6). Additionally, because of its ability to reduce SAR, the use of pTx permits data acquisitions with higher MB factors. Our data suggest that the use of pTx MB3 vs. pTx MB2 to increase SNR efficiency can improve estimations of multiple fiber orientations (Figs. 7 and 8) and that the use of pTx MB4 acquisition is also possible and may be beneficial when compared to the HCP 1Tx acquisition (Fig. 9), although in this study, this high acceleration achieved with MB4 on the transmit side is likely hampered by unaliasing capacity of the receiver array used. Nevertheless, clearly these data indicate that pTx will play a critical role in pushing the spatio-temporal resolutions for ultrahigh field whole-brain dMRI.

Here we utilized the split slice GRAPPA method (36) to reconstruct images for all of the pTx protocols in order to ensure image quality especially for data acquisition with higher MB factors (Supporting Fig. S6). However, the standard slice GRAPPA method was applied for the HCP 1Tx protocol as in the original HCP. To investigate the impact of the two different reconstruction algorithms, we also applied the split slice GRAPPA method to the data acquired in two subjects using the HCP 1Tx protocol. Split slice GRAPPA slightly improved the estimation of fiber orientations (especially for second and third fibers); however, this improvement was sufficiently marginal not to have an impact on the conclusion that the HCP pTx protocol enhances the performance for fiber orientation estimations.

Our data obtained with higher slice accelerations suggest that the use of pTx with MB3 may represent the most preferable configuration when using the Nova 8Tx32Rx coil for HCP-style dMRI with ~1-mm isotropic resolutions. The increased g-factor penalty relative to the MB2 acquisition seems to be well compensated for by the increased SNR efficiency. Further accelerating with MB4 appears to degrade the data quality in central brain regions (Fig. 8, axial slices), likely a consequence of the increased g-factor penalty with this specific coil.

The choice for designing pTx MB pulses for sagittal slices was made because preliminary studies demonstrated an SAR advantage compared to HCP-style oblique axial slices, consistent with previous simulations of similar transmit coil layouts with azimuthally distributed elements (20). Furthermore, designing pulses to image sagittal slices also produced better flip-angle uniformity without any black holes in the brain.

The disadvantage of sagittal slices, however, was the need to acquire slightly more slices (144 sagittal vs. 132 oblique axial slices) to ensure full brain coverage in majority of the subjects; this resulted in a small increase in volume TR (7400 vs. 7000 ms for MB2). Coronal slices would have also facilitated pTx pulse performance for this coil layout; however, we did not choose this orientation because the resulting use of phase encoding in the left-right direction would have been suboptimal with respect to in-plane acceleration performance (4).

All of the pTx dMRI data presented here were acquired in the “protected mode” defined by the manufacturer so as to be conservatively consistent with local-SAR limits during pTx use. During the ~10-minute dMRI data acquisition, we observed that the long-term 6-min total RF power delivery of our pTx MB pulses on average reached up to ~45%, ~68% and ~81% of the maximum allowed value (with 11 W as specified by the vendor for the Nova 8Tx32Rx coil) for the MB2, MB3, and MB4 image protocols, respectively. Consequently, we were also always under the manufacturer allowed short-term 10-sec power limit of this “protected mode”, which is higher (22 W).

In order to further confirm that the local SAR in our acquisition was indeed under the safety guideline limit, we calculated the local 10-g SAR for our imaging protocols by following the same pulse design procedure and RF specifications and sequence timings as in our experiments, but using the electromagnetic simulation of the Nova 8Tx32Rx coil loaded with a human head model (see the local SAR map in Supporting Fig. S7). Our result showed that the maximum local SAR of the three imaging protocols was far under the guideline value of 10 W/kg (as specified for the normal operation mode (37)). The maximum local SAR was 0.95, 1.42 and 1.70 W/kg for the MB2, MB3, and MB4 acquisitions, respectively, corresponding to a safety margin of factor ~10, ~7, and ~5.8, respectively. Given that a safety margin of ~3 has been recommended for pTx pulses and utilized in recent 7T studies to image the human brain (38,39), the high safety margins in our pTx calculations indicate that indeed we were in compliance with the SAR guidelines. More importantly, they suggest that higher MB accelerations and more rapid data collection would be possible with pTx MB pulses provided unaliasing of the signals on the receive-end can be supported within acceptable g-factor noise; this would be feasible with improved receive RF coils (e.g., 7T receive arrays with 64-(40) or larger number of channels), and/or alternative acquisition strategies (41–43). Higher accelerations would be useful especially in human studies that involve elderly or pediatric patients where longer scan times become problematic. In particular, higher accelerations are critical for higher resolution imaging; when combined with novel signal processing methods (44,45), we fully expect that submillimeter dMRI data will be feasible provided higher accelerations with MB4 or higher MB factors can be attained to counter the prolonged data acquisition times that normally accompany collection of more data.

Instead of pursuing higher accelerations, the reductions in SAR obtained with pTx can be traded for shorter, and hence higher power, excitation and refocusing RF pulses so as to improve slice profiles and decrease the echo time. As is well known, the latter would translate into SNR gains in dMRI, especially at 7T where the T₂ values are relatively short (2).

For HCP 1Tx acquisition, we placed three dielectric pads under the head/neck and one pad on either side of the head (five pads in total as in the HCP) to improve the B₁⁺ in the cerebellum and lower temporal lobes. Although effective in in the cerebellum, this arrangement of dielectric pads did not seem to recover fully both temporal lobes. Indeed, we observed a systematic bias across all of the subjects scanned in the current study for better improvements in the left temporal lobe, compared to the right one. It will be interesting to examine whether this bias could be predicted by electromagnetic simulations.

One of the challenges in SMS/MB dMRI acquisition is the high peak RF power associated with the refocusing MB RF pulse, especially when using high MB factors. To reduce the peak power of the pTx MB refocusing pulses, we followed the 7T HCP protocol (4) and incorporated the time shifting strategy (28) into the formation of the channel-specific MB RF waveforms. A phase scrambling strategy, with or without time shifting, can also be employed to reduce peak power for both single-transmit (46,47) and pTx MB pulses (48). Alternatively, one can consider incorporating explicit peak power constraints into the pulse design (49,50) to comply with the hardware limit. Non-conventional MB pulses such as PINS (11), MultiPINS (13) and adiabatic PINS (51) pulses, can also be employed to reduce peak power requirements, albeit at the expense of bandwidth and consequently compromised slice profiles.

In the current study, the pTx MB pulses utilized for dMRI were designed with total RF power control and with single spokes (corresponding to RF shimming for each band). Although these pulses provided better performance (in terms of flip-angle uniformity and SAR) than the single-transmit mode, further optimization is possible. For example, pTx MB pulses can be designed with explicit power related constraints (50,52), especially for local SAR, and applied in the “experimental” mode (another mode available on Siemens step-2 pTx systems to enable data acquisition with real-time local SAR supervision). Even after considering a safety margin of ~3 to account for uncertainties in local SAR estimation (38,39), this strategy should enable faster dMRI acquisitions with higher slice accelerations (e.g., MB5 or 6). Further optimization could also utilize pTx multispoke RF pulses (23,38,53–55) that are capable of additional improvements in RF performance for SMS/MB imaging at 7T (48,56) and above (57).

Conclusions

We have demonstrated the advantages of RF parallel transmission over single-transmit configurations for acquiring HCP-style, high-resolution, whole-brain slice-accelerated diffusion MRI at 7T. Critical to this accomplishment is a synergistic combination of a time efficient slab-wise pTx multiband RF pulse design framework and a pTx-enabled multiband single-shot 2D diffusion weighted EPI pulse sequence. Most notably, our data suggest that pTx can be used not only to improve the estimation of multiple fiber orientations, but also to enable higher slice accelerations. As such, we believe that pTx will have great utility for rapid acquisition of high-quality, high-resolution whole-brain dMRI, desirable for many neuroscience and clinical applications.

Multichannel multislice B1+ mapping

In this study, multichannel multislice B1+ maps were obtained by using a hybrid method, which combines a single large tip angle AFI together with a series of small tip angle gradient echo images. Relevant imaging parameters for the AFI were: FOV=320(RO)×216(PE)×176.4(SS) mm3 (where RO, PE and SS designate readout, phase encode and slice selective dimensions, respectively), in-plane resolution= 4 mm, slice thickness=6.3 mm, TR1/TR2/TE=20/100/2.13 ms, nominal flip angle=60°, in-plane acceleration factor=2 (i.e., iPAT=2 in Siemens terminology), partial Fourier=6/8 (PE and SS), bandwidth=320 Hz/pixel and total acquisition time=3 minutes 11 seconds. The series of small tip angle gradient echo images were acquired with the relevant imaging parameters being FOV=320(RO)×216(PE) mm2, in-plane resolution=4 mm, 24 sagittal slices, slice thickness=6.3 mm, TR/TE=250/2.76 ms, nominal flip angle=10°, iPAT=2, partial Fourier=7/8 (PE), bandwidth=380 Hz/pixel and total acquisition time=1 minute 30 seconds.

T1 weighted 3D-MPRAGE acquisition

The T1-weighted image obtained for masking the brain was acquired using the MPRAGE sequence (1) with the following imaging parameters: FOV=224(RO)×224(PE) ×179.2(SS) mm³, 0.7-mm isotropic resolutions, TR/TE/TI=2400/2.68/1300 ms, nominal flip angle=6°, iPAT=2, partial Fourier=7/8 (PE), phase oversampling=10%, bandwidth=210 Hz/pixel and total acquisition time=6 minutes 36 seconds. To reduce the impact of B₁⁺ inhomogeneity on inversion, adiabatic pulses (2) using the phases obtained from the CP-like mode RF phase shimming were utilized.

Pilot high resolution dMRI with 2-fold slice acceleration

Using each of the three transmit configurations under consideration, we acquired the 1.05-mm, single-shell, whole brain dMRI data with: FOV=210(RO)×210(PE) ×151.2(SS) mm³, anterior-posterior phase encoding, MB2, inter-slice shift=FOV/2, iPAT=3, partial Fourier=6/8, 144 sagittal slices, TR/TE=7400/71 ms, bandwidth=1388 Hz/pixel, and echo spacing=0.82 ms.

As in the 7T HCP dMRI protocol, excitation and refocusing MB pulses were formed using vendor optimized apodized sinc pulses with TBWP=3.2 for excitation, and TBWP=5.2 for refocusing. The pulse duration was set to 5120 Bs for excitation and 10240 Bs for refocusing. Furthermore, a time shift of 1920 Bs was introduced between the two SB pulse components of the final MB2 pulses (3), as in the 7T HCP dMRI data (4), leading to total pulse duration of 7040 Bs for excitation and 12160 Bs for refocusing.

The pTx dMRI dataset was acquired with the pTx-enabled sequence, whereas the two 1Tx dMRI datasets were obtained with the sequence that had been used in the WashU-Minn-Oxford consortium of the HCP (4). For the pTx acquisition, the RF voltages were adjusted to achieve the nominal flip angles (i.e., 90° for excitation and 180° for refocusing) at the maximum B₁⁺ field across the brain. For 1Tx acquisitions, because of the more inhomogeneous RF field across the brain, relatively higher reference RF voltages (set to achieve 10–15% greater than nominal flip angles) were utilized to increase the signals from the low B₁⁺ regions in the periphery of the brain.

For the pTx dMRI acquisition, the same 24 RF shim sets were utilized for both excitation and refocusing. These RF shim sets were utilized to form 12 pairs of band-specific or slab-specific pTx excitation and refocusing MB2 pulses (a total of 48 pTx MB2 pulses). During data acquisition, each pair was applied six times with adjusted central frequencies to excite and refocus the 12, 1.05-mm thick image slices residing within the two corresponding 6.3-mm thick B₁⁺ mapping slabs (each with 6 image slices), leading to the acquisition of a total of 144 image slices per image volume.

Original HCP 7T diffusion protocol

The HCP 7T diffusion protocol acquires whole brain dMRI data with 1.05 mm isotropic resolutions, FOV=210(RO) × 210(PE) × 138.6(SS) mm³, MB2, iPAT=3 (3-fold in-plane acceleration), partial Fourier=6/8, inter-slice shift=FOV/2, 132 oblique axial slices, TR/TE=7000/71 ms, bandwidth=1388 Hz/pixel, echo spacing=0.82 ms, and two-shell q-space sampling (b-value=1000 and 2000 s/mm²); it acquires a total of 286 image volumes, corresponding to 64 unique diffusion directions per shell plus 15 interspersed b=0 images, acquired twice using anterior-posterior (AP) and PA phase encode directions. The total acquisition time was ~40 minutes, which was divided into 4 segments of ~10 minutes each (the reader is referred to Vu et al. (4) for more details on the HCP 7T dMRI protocol).

Supplementary Material

Fig. S1. Magnitude transmit B1 (B1+) maps for Nova single transmit (1Tx) coil alone (top row) and with dielectric padding (middle row), Nova 8 transmit (8Tx) coil with pTx multiband (MB) pulse design (bottom row). B1+ maps are shown in three orthogonal views with brain regions indicated by black curves. Following the slab-wise design framework, band-specific RF shimming was conducted on 24 contiguous, 6.3-mm thick sagittal B1+ mapping slabs covering the whole brain. The brain mask utilized was derived by extracting the brain from a 3D T1w image acquired with 0.7 mm isotropic resolutions. Note that pTx yielded best B1+ homogeneity across the whole brain.

Fig. S2. Comparing HCP 7T dMRI protocol (HCP 1Tx) with HCP pTx protocol in terms of histograms of temporal SNR (tSNR). Each row shows tSNR histograms for one subject. For each subject, the tSNR histogram for HCP 1Tx (blue) or HCP pTx (green) dataset was created by counting the voxels in the brain mask and based on the tSNR map that were calculated on a voxel-wise basis from the corresponding 15, minimally preprocessed, b0 images obtained at different time points during the dMRI acquisition. Further quantitative analysis revealed that the use of pTx on average increased tSNR in ~63% of the brain volume.

Fig. S3. Comparing HCP 7T dMRI protocol (HCP 1Tx) with HCP pTx protocol. Data are shown for another subject. (a) Color fractional anisotropy (FA) maps. (b) Volume fraction maps for second fiber orientations. The color FA is FA (in the range of [0 1]) with the color representing the orientation of the principal fiber (red: left-right; green: anterior-posterior; blue: inferior-superior). The volume fraction map is shown in a colorscale of [0.05 0.2] (with yellow being high and red being low in volume fraction), overlaid on the respective FA map (in a grayscale of [0 1]). Both dMRI datasets were acquired with 1.05 mm isotropic resolutions, MB2, in-plane acceleration factor=3, and TE=71 ms. The TR for pTx acquisition was slightly longer (7400 vs 7000 ms). Both acquisitions utilized the same q-space sampling scheme (double shells, b-value=1000/2000 s/mm2), corresponding to 143 unique image volumes, each acquired twice with anterior-posterior (AP) and PA phase encode directions. Total scan time was kept constant for both datasets (i.e., 40 minutes divided into 4 segments of 10 minutes each). Note that the use of pTx improved fiber orientation estimation performances in such brain regions as the lower temporal lobe, the cerebellum and the inferior frontal lobe.

Fig. S4. Color fractional anisotropy (FA) maps of the HCP pTx MB2 protocol (top row) vs the pTx MB3 protocol (middle row) vs the pTx MB4 protocol (bottom row) in another subject. The color FA is FA (in the range of [0 1]) with the color representing the orientation of the principal fiber (red: left-right; green: anterior-posterior; blue: inferior-superior). All three dMRI datasets were acquired with 1.05 mm isotropic resolutions, in-plane acceleration factor=3, TE=71 ms, and double-shell q-space sampling (b-value=1000/2000 s/mm2). Total scan time was kept constant for all acquisitions (i.e., ~40 minutes divided into 4 segments of 10 minutes each). Because of use of a shorter TR (3701 ms for MB4 and 4934 ms for MB3 vs 7400 ms for MB2), both MB3 and MB4 acquisitions obtained more data than the MB2 acquisition.

Fig. S5. Volume fraction maps of second fiber estimation for the HCP pTx MB2 protocol (top row) vs the pTx MB3 protocol (middle row) vs the pTx MB4 protocol (bottom row) in another subject. These volume fraction maps derived using the same data as in Fig. S4, are overlaid on the respective fractional anisotropy map (defined in the grayscale of [0 1]) and shown in a colorscale of [0.05 0.2] (with yellow being high and red being low in volume fraction).

Fig. S6. Comparison of image quality for pTx acquisition with MB2 vs MB3 vs MB4, all with an in-plane acceleration of 3 (iPAT3). Shown are distortion corrected b=0 images acquired with 1.05 mm isotropic resolutions. Although enabling shorter TR values, both MB3 and MB4 data acquisitions used the same TR of 7400 ms as MB2 acquisition to avoid the TR dependent signal saturation effect for comparison purposes. All images were reconstructed using the split slice-GRAPPA algorithm (Cauley et al. MRM 2014) to minimize the inter-band signal leakage. Note that both MB3 and MB4 acquisitions led to comparable image quality to the MB2 acquisition.

Fig. S7. Maximum intensity projection of the local SAR distribution in axial (left), sagittal (middle) and coronal (right) view for the pTx multiband pulses utilized in the current study. The local SAR map shown here is normalized to the maximum, mainly to appreciate the location of the hotspots. Note the SAR hotspots observed in various regions of the head. This same normalized local SAR distribution applies to all of the pTx dMRI acquisitions in the current study, but the absolute value for the maximum local SAR varies, depending on what MB factor is used for the acquisition. The maximum local SAR value was calculated to be 0.95, 1.42 and 1.70 W/kg for MB2, MB3 and MB4, respectively.