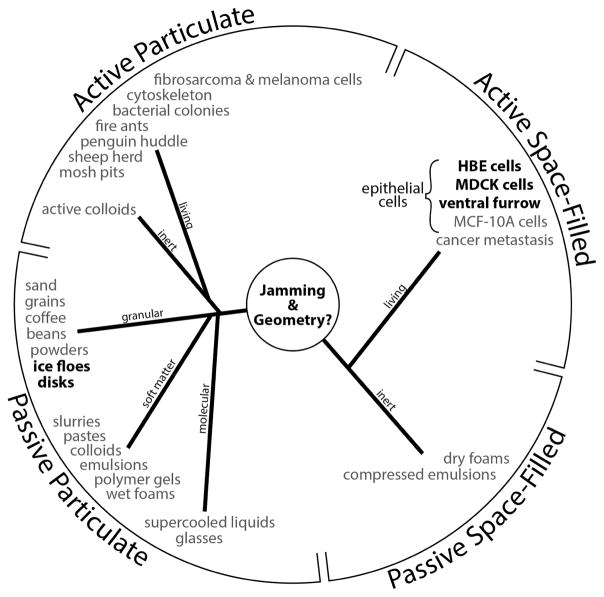
Figure 4. The jamming superfamily.

Each entry denotes a phyical system in which jamming behavior has been reported, and is categorized here into four classes. In bold are systems described in this report; See also Fig. S4. The jamming mechanism was first introduced to explain the poorly understood behaviors that typify certain collective granular systems. Similarities in behavior between such inert granular systems and the migrating epithelial layer were quickly recognized however.^6,38,39 For example, both granular and cellular collective systems are close-packed, volume exclusion prevents two particles (or cells) from occupying the same space at the same time, and particle-particle (cell-cell) interactions are strong. Moreover, just as inert granular systems display swirling motions that arise in cooperative multi-particle packs and clusters, so too does the migrating epithelial layer.^8,40–44 But other physical factors do not fit so easily into this analogy. For example, within granular matter the state of internal mechanical stress is mainly compressive –these are fragile materials in the sense that they can support immense compressive stresses but can support no tensile stress whatsoever– whereas within the confluent cell layer the mechanical stress is overwhelming tensile.⁴² Within granular matter a principal control variable for jamming is free space between grains^2,45 whereas in the fully confluent cell layer there is by definition no free space between cells. Within granular matter neither a change of particle shape nor mutual particle-particle adhesion is required for jamming or unjamming – although either can influence jamming dynamics⁴⁶– whereas cell shape change and cell-cell adhesion are thought to be indispensable features of epithelial function and jamming ^5,24–26. And perhaps most importantly, the granular particle is neither active nor self-propulsive nor mechanosensitive whereas the epithelial cell exhibits all of these characteristics. In this report we show that the behavior of these diverse living and inert systems is unified to a remarkable extent by consideration of system geometry.