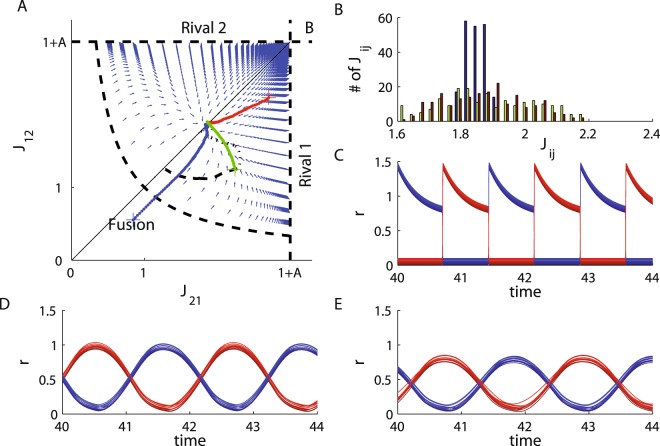
Figure 5.

Numerical simulation of STDP dynamics. We solved the STDP dynamics numerically, Eq. (11), with N₁ = N₂ = 10, α = 0.9, τ₊ = 0.5 and τ₋ = 1. The cross-correlation functions were evaluated numerically using the separation of time scales. For each update step of the synaptic weights, the cross-correlations were evaluated by numerically solving the 2(N₁ + N₂) dynamics of the neuronal firing rates, Eqs (1–4), with fixed values for the synaptic weights with I = 2, A = 2 and $ϵ=0.001$. (A) Trajectories of the order parameters, $J_{ij}=\frac{1}{N_1{N}_2}{\sum }_{x,y}{J}_{ix,jy}$, for five simulations are plotted on the phase diagram and the flow chart. The red, green and blue traces depict the learning dynamics of the same model with $ϵ=0.001$ from different initial conditions (marked by +). The dashed black curve depicts the learning dynamics of the order parameters with $ϵ=0.2$. The dotted black curve depicts the learning dynamics of the order parameters for a model with a local inhibition term $J_{\mathrm{loc}}=0.5$, and $ϵ=0.2$. The vector field shows the STDP flow for $ϵ=0$ calculated using the analytic expressions for the correlations, subsection Calculation of the cross-correlation function in Methods. (B) Synaptic weight distribution for the three examples with $ϵ=0.001$ in A (red, green and blue), differentiated by color. (C) Neuronal dynamics at the STDP fixed point for the slow adaptation case, $ϵ=0.001$. The firing rates of the N₁ population 1 neurons (red traces) and N₂ population 2 neurons (blue traces) in arbitrary units are shown as a function of time. Since the firing rates of different neurons from the same population overlapped, we shifted them vertically for purposes of visualization. For the three different initial conditions (with $ϵ=0.001$) illustrated in A the oscillation period was T = 1.433, T = 1.432, and T = 1.436, and all units of time are measured in units of τ_a. (D) Neuronal dynamics with $ϵ=0.2$ at the STDP fixed point. The firing rates of the N₁ population 1 neurons (red traces) and N₂ population 2 neurons (blue traces) in arbitrary units are shown as a function of time. The firing rates of different neurons were shifted vertically for purposes of visualization. The oscillation period was T = 2.165 in units of τ_a. (E) Neuronal dynamics with local inhibition, J_loc = 0.5, and $ϵ=0.2$ at the STDP fixed point. The firing rates of the N₁ population 1 neurons (red traces) and N₂ population 2 neurons (blue traces) in arbitrary units are shown as a function of time, see subsection Neuronal dynamics with local inhibition term in Methods. The firing rates of different neurons were shifted vertically for purposes of visualization. The oscillation period was T = 2.17 in units of τ_a.