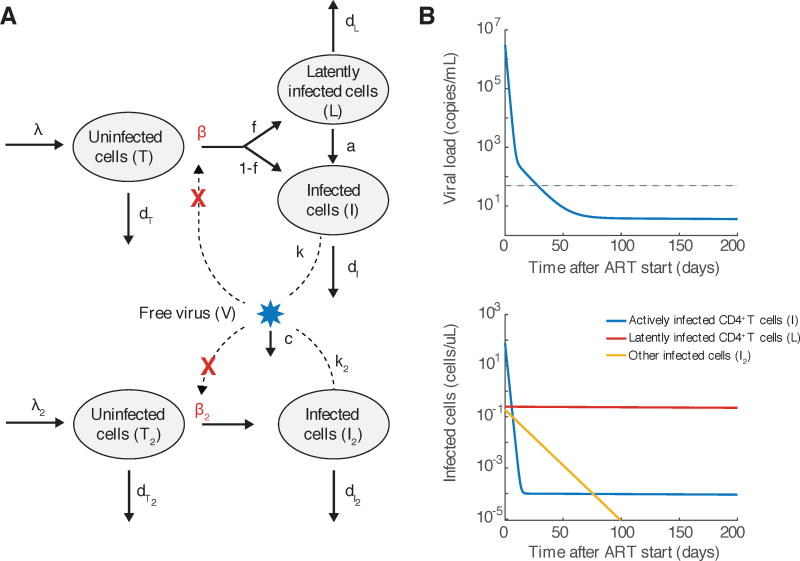
Fig. 2.
An augmented model of viral dynamics that takes into account multiple populations of infected cells. A) Flow diagram of processes that occur in the model, as described in Box 2. Adapted from Perelson et al [93]. B) Multiphasic decay of viral load predicted by the model. C) Decay of individual populations of infected cells predicted by the model. Graphs were generated by numerically integrating Equation 5 with parameters approximately consistent with those estimated in Andrade et al [6]. We assumed that other target cells (I2) live 10x longer with or without infection, exist at 1000x lower level before infection, produce virus at 10x slower rate, and are infected at the same rate. 1 in 10,000 infections result in latency, and that latently infected cells (L) live 10,000 times longer than actively infected cells. Parameters are λ = 100 cells/uL, β = 10−7 or 0/day/(virus/mL), k = 1000 virus/cell, dT = 0.1/day, dI = 1/day, λ2 = 0.01 cells/uL, β2 = 10−7 or 0/day/(virus/mL), k2 = 100 virus/cell, dT2 = 0.01/day, dI2 = 0.1/day, c = 25/day, f = 10−4, a = 4 × 10−4/day, dL = 10−4/day.