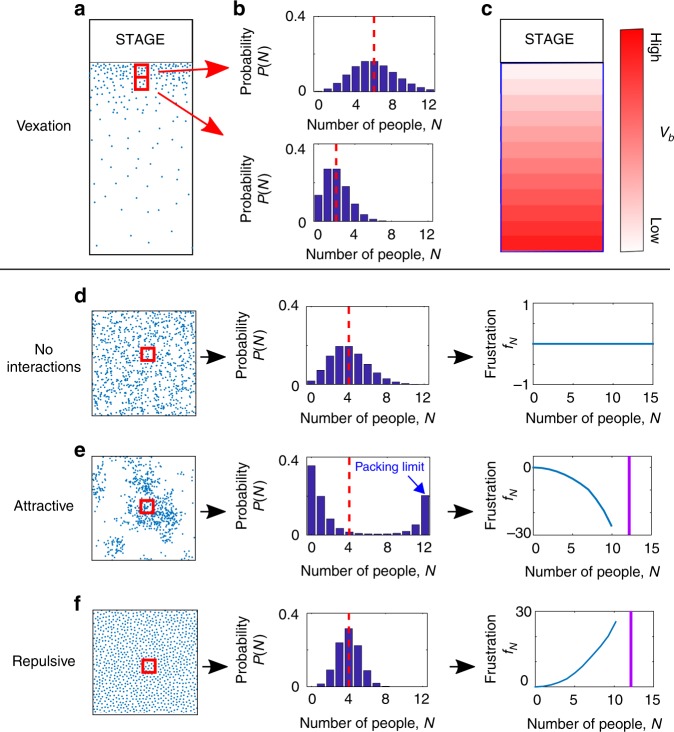
Fig. 1.
Resulting density-functional approach. a Schematic of crowd in which agents attempt to get as close to the stage as possible while avoiding overcrowding. b In the absence of interactions, the mean of each probability distribution (vertical dashed line) indicates location preference, from which we can extract a bin-dependent vexation functional, vb. c Resulting bin-dependent vexations. d–f Crowds in environments with uniform vexation but with neutral, repulsive, or attractive interactions. For neutral interactions, we expect complete spatial randomness leading to Poisson distributed counts within each bin. The repulsive and attractive interactions are thus reflected in the deviation of the probability distribution from the Poisson form26. From these deviations we can extract a bin-independent frustration functional, fN, whose curvature indicates the nature and intensity of the interaction