An Alternative Approach for the Analysis of Time-to-Event and Survival Outcomes in Pulmonary Medicine

To the Editor:

For many pulmonary illnesses, the time to an event, such as death, is of primary interest. Visually, the Kaplan-Meier survival curve is an essential tool to assess time-to-event data (1). However, summarizing the difference of a time-to-event outcome between study groups can be challenging. For example, although the log-rank test compares survival curves, this test does not provide an estimate of the effect of an exposure (i.e., treatment effect estimate) (2). The Cox proportional hazards regression model does provide an effect estimate in terms of the hazard ratio (HR), defined as the ratio of two instantaneous rates of an event at any time during follow-up (3). However, without knowing the event rate in the reference group, the HR can be difficult to interpret and place into context. Further, a key assumption of the Cox proportional hazards model is that the HR is constant between study groups over time (i.e., the proportional hazards assumption). When this assumption is violated, a situation that is not uncommon, results can become distorted and misleading (4). Another common metric, the median survival time, requires sufficient follow-up for survival to be less than 50% to be estimated.

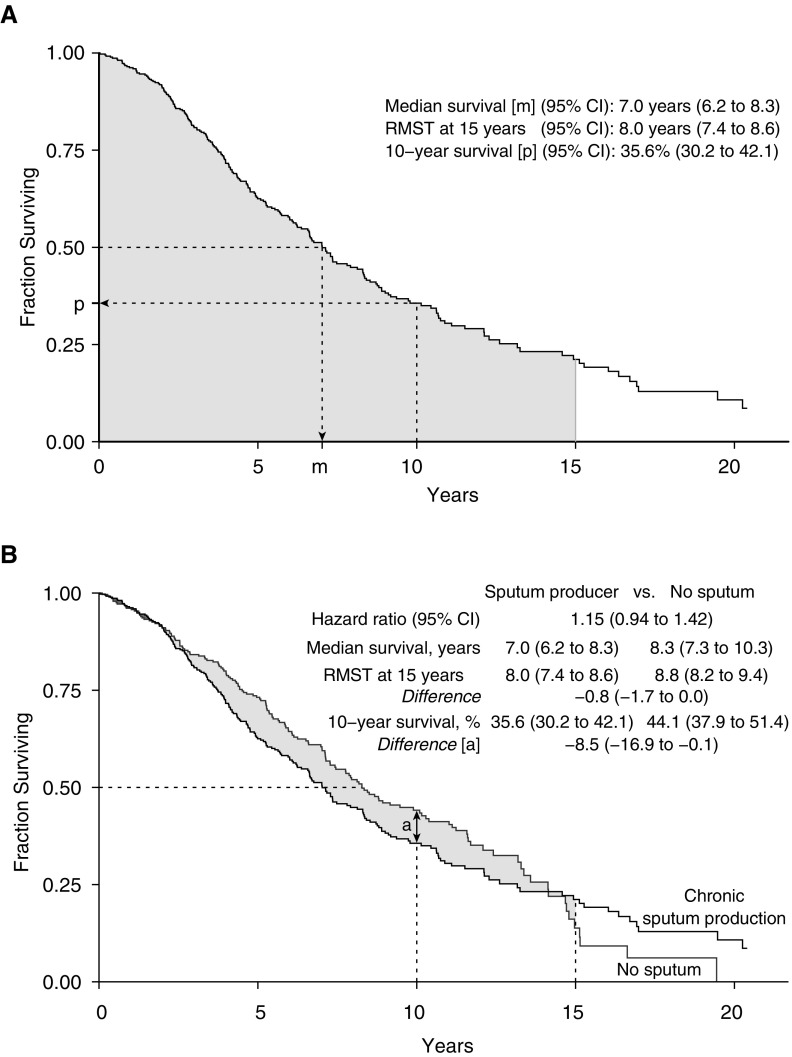
The restricted mean survival time (RMST) estimate is an alternative approach that has not been widely applied in the field of pulmonary medicine. Graphically, the RMST represents the area under the survival curve and is interpreted in simple terms: the average time until an event occurs during a defined period ranging from time 0 (i.e., the start of follow-up) to a specific follow-up time point (τ) (4–10). Thus, the RMST is the τ-specific life expectancy for a study group. For example, the gray area under the Kaplan-Meier curve in Figure 1A demonstrates the 15-year RMST in our first example.

Figure 1.

Unadjusted survival analysis of (A) patients who produced sputum and then (B) in comparison with those who did not produce sputum in the London chronic obstructive pulmonary disease cohort. (A) Three descriptive measures derived from a Kaplan-Meier survival curve for those individuals with chronic sputum production only. The shaded gray area under the Kaplan-Meier survival curve represents the 15-year restricted mean survival time (RMST), m indicates the median survival time, and p indicates the proportion of individuals alive halfway through the follow-up period at 10 years. (B) Shaded gray area illustrates the RMST difference through 15 years. This quantity is the difference between the area under the Kaplan-Meier curves for the two groups. CI = confidence interval.

A comparison of the RMST between two study groups provides an estimate of the duration of time gained or lost that is associated with an exposure, and can be expressed on the absolute difference scale (Equation 1) or relative ratio scale (Equation 2):

$$\text{restricted}\text{life}\text{expectancy}\text{difference}=\text{RMST}\text{group}2-\text{RMST}\text{group}1$$ (1)

$$\text{restricted}\text{life}\text{expectancy}\text{ratio}=\text{RMST}\text{group}2/\text{RMST}\text{group}1.$$ (2)

Methods

To illustrate the RMST approach, we examined unadjusted differences in survival in two cohorts of patients with pulmonary illnesses. These analyses were for illustrative purposes only and do not represent formal assessments of clinical hypotheses. The first sample included individuals in the London chronic obstructive pulmonary disease (COPD) cohort with moderate to very severe COPD, and we compared survival among those who chronically produced sputum with that among those who did not. The second sample included individuals who received a single lung transplant in the United States between 2005 and 2016 (after implementation of the lung allocation score in May 2005), using the United Network for Organ Sharing registry, and we compared posttransplant survival based on age at transplantation.

Results

In the first example, we analyzed 373 deaths among 661 patients in the London COPD cohort during a follow-up period of 20.4 years (ending in March 2016; Figure 1). The Kaplan-Meier plot showed that the survival curves crossed at Year 14 of follow-up, and the proportional hazards assumption was not met (Grambsch-Therneau test, P = 0.026; Figure 1B). Thus, we were analytically limited to an examination of time-specific differences in survival, the median survival times, or the RMST estimates. Time-specific survival proportions and the median survival time only summarize the data at a single point on an entire survival curve. In contrast, the RMST incorporates all past information provided by the survival curve. However, an important consideration when reporting the RMST is the selection of the time horizon. As the survival curves crossed late in the study period, when a limited number of individuals remained under follow-up, we felt it was reasonable to report the 15-year RMST in this example as a summary of the long-term difference in mortality. The 15-year RMST difference showed that, on average, sputum producers lived 9.6 fewer months than nonsputum producers (illustrated by the shaded area in Figure 1B; 8.8 yr − 8.0 yr = 0.8 yr × 12 mo/yr = 9.6 mo). However, if researchers encounter crossing or changing curves in an analysis that they believe might reflect different and biologically plausible survival trajectories, they could still use the RMST to estimate effects over separate periods (e.g., early and late effects) (4).

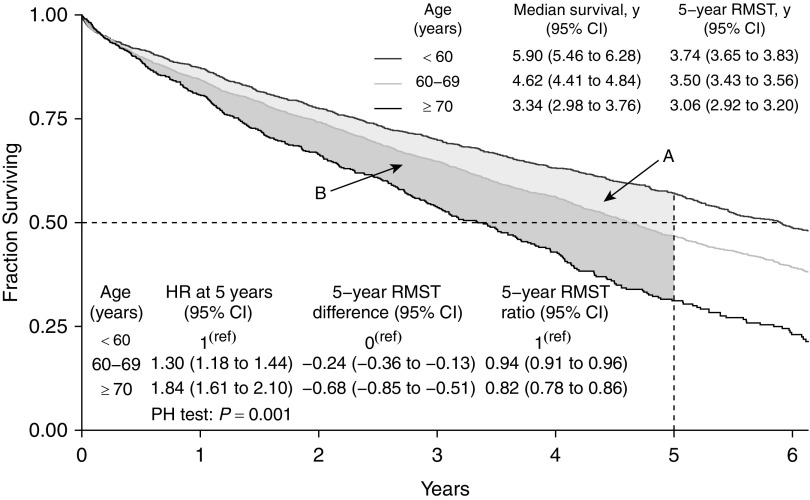
In our second analysis, we examined 5-year, age-stratified survival curves for 5,938 individuals who received a single lung transplant in the United States between 2005 and 2016 (Figure 2). Here again, we found that the proportional hazards assumption was not met (Grambsch-Therneau test, P = 0.001). Further, we could not calculate the median survival time for the youngest age group, as it occurred after 5 years of follow-up. Therefore, we used the RMST method, which showed that the 5-year life expectancy after a transplant was 3.74 years (95% confidence interval [CI], 3.65–3.83), 3.50 years (95% CI, 3.43–3.56), and 3.06 years (95% CI, 2.92–3.20) among individuals aged <60, 60–69, and ≥70 years at the time of transplant, respectively. These RMST estimates showed that transplant recipients aged <60 years lived an extra 8.2 months on average (0.68 yr × 12 mo/yr; 95% CI, 6.1–10.2 mo extra) compared with recipients ≥70 years of age on the absolute scale (using Equation 1). The 5-year life expectancy for recipients aged 60–69 years was 6% shorter (ratio = 0.94; 95% CI, 0.91–0.96) on the relative scale (using Equation 2).

Figure 2.

Unadjusted survival analysis of individuals who received a single lung transplant in the United States between 2005 and 2016. We excluded concurrent multivisceral, pediatric, and retransplants. This figure illustrates both the difference and ratio of the restricted mean survival time (RMST) estimates between individuals <60, 60–69, and ≥70 years of age at the time of his/her transplant. The light gray area (region A) is the RMST difference between those <60 and 60–69 years of age at the time of transplant. The darker gray area (region B) is the RMST difference between those 60–69 and ≥70 years of age at the time of transplant. The difference between those <60 years and ≥70 years of age at the time of transplant is the summation of these two areas. CI = confidence interval; HR = hazard ratio; PH = proportional hazards; y = years.

Discussion

As shown in these examples, the RMST offers several inferential advantages over other time-to-event statistics. Although we examined survival, any time-to-event endpoint can be assessed using the RMST approach. Statistical inference (i.e., estimation and hypothesis testing) using the RMST, including P values, confidence intervals, and covariate adjustment, can be performed in most popular statistical software packages, such as R (11) and STATA (4, 12). Study group comparisons using the RMST estimate also confer comparable statistical power to the log-rank test and test for the HR in many situations (13, 14), thereby providing an alternative and clinically meaningful measure of time gained or lost to inform research and patient care.