Efficient and Fair Heart Allocation Policies for Transplantation

Abstract

Background: The optimal allocation of limited donated hearts to patients on the waiting list is one of the top priorities in heart transplantation management. We developed a simulation model of the US waiting list for heart transplantation to investigate the potential impacts of allocation policies on several outcomes such as pre- and posttransplant mortality. Methods: We used data from the United Network for Organ Sharing (UNOS) and the Scientific Registry of Transplant Recipient (SRTR) to simulate the heart allocation system. The model is validated by comparing the outcomes of the simulation with historical data. We also adapted fairness schemes studied in welfare economics to provide a framework to assess the fairness of allocation policies for transplantation. We considered three allocation policies, each a modification to the current UNOS allocation policy, and analyzed their performance via simulation. The first policy broadens the geographical allocation zones, the second modifies the health status order for receiving hearts, and the third prioritizes patients according to their waiting time. Results: Our results showed that the allocation policy similar to the current UNOS practice except that it aggregates the three immediate geographical allocation zones, improves the health outcomes, and is “closer” to an optimal fair policy compared to all other policies considered in this study. Specifically, this policy could have saved 319 total deaths (out of 3738 deaths) during the 2006 to 2014 time horizon, in average. This policy slightly differs from the current UNOS allocation policy and allows for easy implementation. Conclusion: We developed a model to compare the outcomes of heart allocation policies. Combining the three immediate geographical zones in the current allocation algorithm could potentially reduce mortality rate and is closer to an optimal fair policy.

Heart failure is a progressive disease that affects 5.8 million people in the United States, with 550,000 new cases diagnosed annually. Heart transplantation is a life-saving treatment and improves the quality of life and survival of late-stage heart failure patients.¹ The source of hearts for transplantation is from cadaveric donors, with patients joining the waiting list to receive a cadaveric donor heart.

Since 2004, the number of new active adults (18+) joining the waiting list has increased by 40%. However, the donation rate remains flat with 3.5 donations per 1,000 deaths in 2012, which increased the size of the waiting list by 25%.² According to the United Network for Organ Sharing (UNOS) data, since 2006 to 2014 a total of 27,119 adult patients has joined the waiting list, which is significantly larger than 18,962 heart donations during the same period. As of 1 December 2016, 3,773 adult patients are on the UNOS heart transplantation waiting list. These numbers clearly indicate a major imbalance in supply and demand resulting in a substantial mortality for the patients on the waiting list.² This shortage of supply raises the allocation question, “Which patients should receive priority when a donor heart becomes available?” This allocation problem is one of the top priorities in heart transplant management.²

To enhance the fairness of organ allocation, the National Organ Transplant Act enacted new rules to ensure fair and equitable distribution of available organs.³ Moreover, the allocation should be based on a priority rule for patients on the waiting list; that is, if an organ is procured, patients should be ranked and the organ is offered to the highest priority patient until it is accepted.⁴ Allocation policies, which substantially affect the quality-adjusted life years of the population, should provide fair access to organs to all patients, independent of their race, age, and other characteristics. Faced with such challenges, policy makers in UNOS have periodically revised their policies over time.⁵ The original heart allocation system, approved in 1988, was a two-tiered policy using medical emergency status applied to both adults and pediatrics.⁵ In 1989, UNOS/OPTN (Organ Procurement and Transplantation Network) implemented the heart allocation policy to place the highest priority on those patients who are most likely to die while waiting.⁶ In 1998, this allocation method was restructured into a three-tiered system (status 1A, 1B, and 2) in which higher priority was assigned to the sickest patients with a short survival rate.⁷ Details of the revisions to heart allocation policy from 1988 to 2012 are provided by Colvin-Adams and others.⁵ The current UNOS allocation policy was issued in July 2006, allowing a broader regional sharing of donor hearts.⁸ However, the optimality of the current UNOS practice in terms of efficiency and fairness is not clear, and the OPTN/UNOS Heart Subcommittee recently suggested a reassessment of the current allocation policy.¹ Meyer and others⁹ studied the limitations of the current three-tiered medical urgency system and depicted the future direction of heart transplantation in the United States.

As assessing the performance of allocation policies for the nation is not amenable to clinical trials, researchers have developed simulation models to analyze allocation policies. For example, the Thoracic Simulated Allocation Model is a model of heart allocation system from 1 July 2009 to 30 June 2011, which has been used to evaluate the proposed changes in policy. The Thoracic Simulated Allocation Model makes the following assumptions: 1) arrivals of candidates/donors are input to the model with a data file, 2) the initial waiting list is input to the model with a data file, and 3) an entire history of waiting list status changes must be input to the model for each patient. As a result, in each simulation, the same actual donors and candidates are used; thus, statistical tests of comparisons are not possible.¹⁰ We relaxed those assumptions by developing models for arrivals of patients and hearts, as well as models for change of health status in the waiting list. van den Hout and others¹¹ built a model for the Eurotransplant waiting list for heart transplantation and showed that international organ exchange reduces waiting list mortality in different countries by 1.9% to 12.4%. Shechter and others¹² created a simulation model for the liver allocation system to compare the performance of different allocation policies in liver transplantation. Su and Zenios¹³ built a mechanism design model to examine the effect of posttransplant information asymmetry on the kidney allocation system in terms of efficiency and equity. Bertsimas and others¹⁴ developed a framework to derive optimal policies for kidney allocation while considering fairness constraints.

In this study, we developed a simulation model of the US heart allocation system and validated it to evaluate the potential impacts of allocation policy modifications on several outcomes such as pre- and posttransplant survivals. We used the current UNOS allocation policy as the baseline policy for our simulation model. With a few exceptions, this policy ranks patients in three different levels, that is, geographical (proximity to the donor hospital), health status, and waiting time level. Specifically, when a donor heart becomes available for transplantation, the policy first categorizes patients on the waiting list based on their distance from the procurement Organ Procurement Organization (OPO) into six zones, where each zone includes all transplant centers within some distance of the donor hospital. Note that these zones are not geographical districts but are defined by proximity to the donor hospital. It first offers the procured heart to the patients who are in the Designated Service Area (DSA) of the same OPO as the heart is (Zone DSA); if no one is matched, the heart will be offered to the patients of Zone A; if still no match is found, it will be offered in hierarchy to patients in Zones B, C, D, and E. At each zone it classifies patients by their health status and then primary and secondary blood type match with the donor heart. Within each classification, patients are ranked by the total waiting time accumulated at that health status (see Appendix H for details).

In addition to the current UNOS practice in allocating donor hearts, we considered three additional heart allocation policies based on modifications of the current practice. Specifically, Policy I preserved the current prioritization rule but combined Zones A, B, and C into one zone. Policy II preserved the current prioritization rule but changed the priority of health status from 1A > 1B > 2 to 1B > 1A > 2. Policy III preserved the current allocation prioritization but prioritized waiting time over health status. Furthermore, we provided a framework to analyze the fairness of allocating donor hearts by adapting similar concepts in the context of general resource allocation with a single decision maker and multiple self-interested players.

Methods

Because the heart allocation system is complex with several components such as queues and allocation schemes, we designed a simulation model to represent its behavior. Data from several sources are used to calibrate and validate the model from 2006, the last year in which changes to the heart allocation policy were made,¹⁵ to the end of 2014. Patient records for 30,394 adults who are reported in the UNOS database were used. Among these patients, 2,623 died while waiting on waiting list and 17,667 went under transplantation. Also, the Scientific Registry of Transplant Recipient (SRTR) annual data reports were used to obtain more detailed information about the patients on the waiting list, as well as the organ donation process.¹⁶ Patient survivals were estimated using risk adjustment models provided in the SRTR database.¹⁷

Overview of the Model

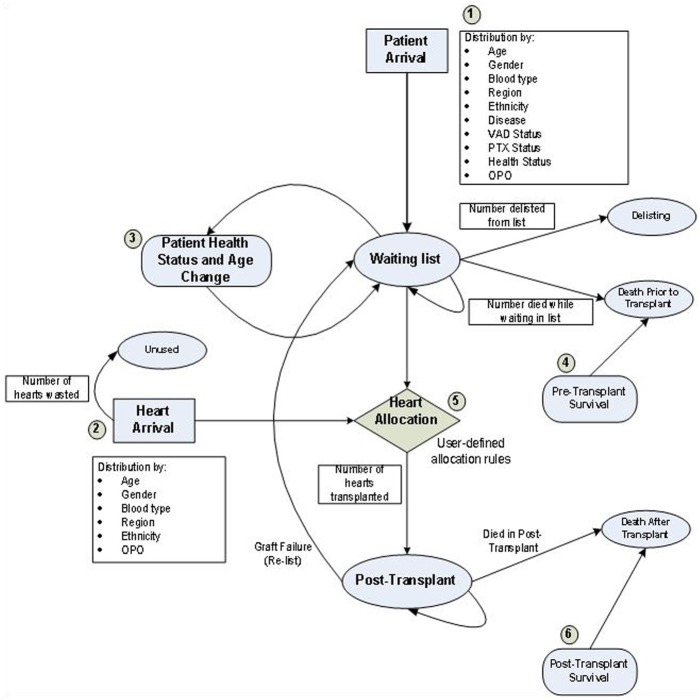
In order to design a flexible model to test the performance of a broad class of allocation policies, we developed a simulation model of the heart allocation process on a daily basis. The simulation model consists of six main modules: patient arrival, heart arrival, patient’s health status change, pretransplant survival, heart allocation, and posttransplant survival. Each module consists of several submodules interacting together to simulate the allocation system (Figure 1).

Figure 1.

The simulation model for heart transplantation waiting list has six main modules: the patient arrival, heart arrival, patients’ health status change, pretransplant survival, heart allocation, and posttransplant survival modules. Numbers on the figure correspond to the core modules of the simulation model.

Patient Arrival Module

This module generates patient arrivals to the waiting list and assigns various clinical and demographic attributes according to conditional distributions. We modeled patient arrivals as a nonstationary Poisson process (commonly used for modeling arrivals¹⁸) with the arrival rate depending on year. Daily arrival rates for the patient arrival process were estimated by dividing the yearly arrival rates by 365 (see Appendix I for sensitivity analysis on patient arrival rates). We validated the model by comparing the outcomes generated by the model with that observed in historical data. Each patient joining the waiting list has several characteristics and attributes such as age group, gender, disease type, ethnicity, blood type, region, ventricular assist device status, pretransplant status, waiting time, and health status. UNOS considers more than 70 disease groups for classifying the patients. Because the sample sizes in each group were not enough to design statistical distributions, we aggregated these 70 groups into 9 broader groups according to the organ data source of the UNOS (Appendix A). At the time of listing, each patient is assigned with one of four health statuses used by the UNOS to represent the health condition of a patient joining the waiting list. For details on medical criteria to assign a patient’s health status, see Appendix A.

The patient arrival module considers some hierarchal and conditional distributions to assign attributes to patients (Figure A.3 in the appendix). At the first level, regression was used to test the time-dependency of each attribute, and then the chi-squared independence test was used for each pair of attributes to assess the dependency among attributes. Among all the attributes, disease group, ventricular assist device status, pretransplant status, gender, and arrival rates depended on calendar year. The distribution of each of these attributes for each calendar year was generated based on historical data. Health status and age distributions were conditioned on disease group and the conditional distributions derived from historical data. After obtaining the distribution of age group conditioned on the disease type, patient age was generated from a continuous uniform distribution for each age group. Ethnicity and blood type are conditioned on gender, and their distributions were derived based on gender distribution. The conditional region distribution was obtained using annual arrival rates. In order to estimate the conditional distributions for each OPO, we aggregated the patient arrivals of all the hospitals in that OPO. Hence, when a patient’s region was determined, the patient’s OPO was generated according to the conditional distributions (Figure A.3 in the appendix). Appendix B elaborates on statistical dependency tests and creation of such a hierarchy.

Heart Arrival Module

This module generates a newly donated heart and assigns its attributes that will be used in the allocation process. Similar to the patient arrival module, each donated heart has several attributes such as donor age, gender, blood type, region, ethnicity, and OPO.

Donated hearts arrive according to a nonstationary Poisson process varying by year, and the daily arrival rates are estimated by dividing the yearly rates by 365 (see Appendix I for sensitivity analysis on heart arrival rates). UNOS data sets consider hearts from pediatric and adult donors as the source for donated hearts. As we only considered the hearts from adult donors, we adjusted the yearly arrival rates of hearts to account for this issue, as well as heart wastage. We did not include the decision processes of patients in accepting/rejecting the offered heart, which depends on the patient and heart characteristics, as well as geographical remoteness. However, extending our simulation to incorporate such decisions is straightforward. Conditional arrival distributions for each heart attribute were estimated from historical data. Similar to the patient arrivals, at the first level, the time-dependency of each attribute was tested using regression. Results showed that blood type, age, and ethnicity depend on calendar year, and each distribution was estimated via historical data. The chi-squared test was then used to analyze the dependency of each pair of attributes in the heart arrival process to create the second-level conditional distributions. At the second level, donor region and gender depended on blood type and age, respectively (Figure A.4 of the appendix). Appendix C elaborates on statistical tests and conditional distributions.

Patient Health Status Change Module

The UNOS considers four medical urgency (health) statuses for the patients on the waiting list: 1A, 1B, 2, and Inactive. Health status 1A is for the patients with the most urgent health status. These patients are mostly in hospitals requiring multiple intravenous medications and have some sort of mechanical assist devices in their heart. Health status 1B is for the patients with less urgent health status, who could be possibly at home using left ventricular assist devices or multiple intravenous medications. The least urgent patients are assigned with the health status 2. A patient who has already been evaluated and accepted by a transplant center, but cannot receive a heart, is assigned with the Inactive health status. For instance, if a patient has another active illness or infection that can possibly jeopardize the transplant process, she or he will be assigned with this health status. Requirements for each health status are described in detail in OPTN policies⁴ (see Appendix A for more details). However, the health status of a patient may change while waiting for transplant. We modeled the daily health status progression of patients on the waiting list as a Markov chain and used UNOS/SRTR data sets to estimate its transition probability matrix via maximum likelihood estimator.¹⁹ In particular, we used the frequency of health status changes between each pair of health statuses over time. Therefore, the module observes the health status of each patient at the start of each day and determines her health status at the next day according to a transition probability matrix. This module was validated by comparing the portion of patients in each health status produced by the model with that observed in historical data (Table A.19 in Appendix D).

Pretransplant Survival and Delisting Module

In the absence of transplantation, removal of a patient from the waiting list may be due to death or delisting. Different allocation policies induce different death and delisting distributions. Therefore, in order to study the impacts of allocation policies on waiting list outcomes, one cannot directly use historical data for death and delisting distributions.²⁰ We estimated the probability of death via Cox proportional hazard models. In particular, we used the risk adjustment models of SRTR for estimating death probabilities.¹⁷ We included all covariates of the Cox model regardless of statistical significance because the magnitude of the proportional hazards is more important. The baseline hazard function was estimated from the Centers for Disease Control and Prevention data sets.²¹ Appendix E provides details regarding pretransplant survival.

Delisting from the waiting list may occur as the patient has clinically improved or became too ill to transplant. Annual number of delisted patients was used to estimate yearly delisting distributions. Also, chi-squared tests revealed a significant correlation between delisting and health status. Therefore, we produced annual delisting distributions for each health status (Appendix E). Death and delisting modules were validated by comparing the outcomes produced by the model with those observed in historical data. This module at the start of each day generates the probability of death and delisting for each patient and updates the list accordingly. If none of these events happen, the health status, waiting time, and age of the patient is updated and she or he moves to the next period (day) (see Appendix F for details).

Heart Allocation Module

Upon procurement of a donor heart to the system, this module ranks the patients on the waiting list and offers it to the highest ranked patient. Because one of the purposes of this study was to analyze the performance of any allocation policy, we used object-oriented programming to create a flexible framework such that any combination of attributes could be used to rank the patients. The current UNOS allocation rule was used as the baseline. With a few exceptions, the allocation process uses the following hierarchy. Once a heart is procured in an OPO, it is offered to a suitable candidate (based on prioritizing health status and considering primary and then secondary blood type match with the donor) that is registered on the waiting list of the same OPO. If the heart is not matched or accepted at the procurement OPO, it is offered to larger areas with a hierarchy until it is accepted and a match is found (see Appendix H for details).

Posttransplant Survival Module

In the model, after receiving a donor heart, patients enter the posttransplant phase. This module keeps track of these patients and estimates their survival. To that end, we used the Cox proportional hazard models reported in SRTR database¹⁷ to estimate the death probabilities after transplantation. Similar to the pretransplant survival module, all covariates were incorporated regardless of their statistical significance, and the baseline hazards were estimated via the Centers for Disease Control and Prevention database.²¹ Therefore, at the start of each day, this module generates the probability of death for each patient after transplantation, and if a patient dies in a period, both the patient and graft are removed from the system as organs are never transplanted more than once. Note that, however, we did not consider graft survival and instead considered the patients who relist (after transplanted with a heart) in the patient arrival module as UNOS data sets provide the arrival of patients demanding a re-transplant (see Appendix G for details).

Allocation Policies

Policy I

The geographical configuration of zones is a critical aspect in the heart allocation system. An ideal zone is a geographically small one with a large population as the likelihood of finding a match is higher and transportation time is short. We propose a three-tiered zone allocation system: If a donor heart is matched with no one in its DSA, it is offered to Zone 1 (union of Zones A, B, and C of UNOS allocation rule). Similarly, if it is not matched with a patient in Zone 1, it is offered in hierarchy to patients in Zone 2 (Zone D of UNOS allocation rule) and Zone 3 (Zone E of UNOS allocation rule). Note that in each zone we considered the same health status, blood type match, and waiting time prioritization rules as the UNOS. The rationale behind combining Zones A, B, and C to form Zone 1 is that the 4- to 6-hour cold ischemic time for a heart is equivalent to approximately 1,500 airline miles¹⁰ (Zone C also contains all transplant hospitals within 1,500 miles of the donor hospital). A similar approach is proposed for patients who are multilisted for kidney transplantation²² (see Appendix H for details). In Appendix I, we conduct sensitivity analysis on priority zones combinations.

Policy II

To prioritize patients according to their health status, the UNOS gives the first priority to health status 1A, the second priority to health status 1B, and finally the third priority to health status 2. The patients assigned with health status 7 (Inactive) are not considered in the heart-patient matching algorithm. This allocation rule gives priority to patients with a higher medical urgency status. However, it has led to a significant imbalance in the distribution of donated hearts. In particular, more than 67% of all transplants correspond to status 1A, while status 1A patients are only 10% of those on the waiting list. Moreover, less than 30% of all transplants correspond to health status 1B, while these patients comprise 40% of the waiting list. This disparity has caused some patients in status 1B relocate together with their families to other regions with shorter waiting time.¹ Also, prioritizing the sickest patients may not be optimal as they may experience a shorter posttransplant survival compared to status 1B patients. Thus, in Policy II we followed the UNOS allocation system except that status 1B was prioritized over 1A in each classification (see Appendix H for details).

Policy III

In the current UNOS allocation policy, waiting time is the last priority. Prioritization based on waiting time is unclear as van den Hout and others²⁰ wrote, “Waiting time as an allocation factor has been a point of discussion for more than a decade.” Policy III considered the UNOS allocation rule except that in each zone waiting time is prioritized over health status, that is, considering primary and secondary blood type match, patients are ranked first by longer waiting time (see Appendix H for details).

Model Validation

In order to compare the outcomes of the proposed allocation policies, we wanted to ensure that the difference between policy outcomes is because of the real performance differences of policies rather than randomness in the model. We used the standard variance reduction techniques to decrease the effects of randomness in outcomes of allocation rules.¹² Because patient and donor heart arrivals were assumed to be independent of the allocation policy, one stream of random numbers was used to produce the patient population and another stream of random numbers was used to produce the donor hearts across all policies.

Once we combined all the modules, we validated the simulation model by comparing its outcomes with the historical data for several measures, such as the number of patients on the waiting list at the end of each year, yearly patient arrivals, yearly heart arrivals, number of transplants performed at each year, number of deaths on waiting list at each year, and 1- and 5-year posttransplant survivals. The simulation was run 30 times using the current UNOS allocation policy, and the average and standard deviation of the 30 replications were reported (Table 1). We also conducted statistical t tests to check the statistical difference between real data and simulation outputs (Table 2).

Table 1.

Validation of Model Results

Outcome Measure	2006	2007	2008	2009	2010	2011	2012	2013	2014
New patients arrival
UNOS	2,554	2,633	2,825	2,966	3,029	2,894	3,115	3,373	3,730
Model mean ($\overline{x}$)	2586.30	2733.73	2953.70	3035.83	3129.50	2907.36	3293.83	3544.36	3816.10
Model standard deviation (s)	50.53	61.03	57.88	59.24	63.23	61.89	52.84	49.35	67.28
Difference (%)	1.24	3.68	4.35	2.30	3.21	0.45	5.42	4.83	2.25
Diseased donors arrival
UNOS	1,893	1,938	2,100	1,958	2,080	2,084	2,165	2,307	2,437
Model mean ($\overline{x}$)	1897.00	1944.50	2107.60	1968.03	2072.10	2080.10	2158.53	2295.76	2429.43
Model standard deviation (s)	36.81	42.30	42.61	49.22	52.61	48.17	43.62	45.58	55.49
Difference (%)	0.21	0.33	0.36	0.50	−0.38	−0.18	−0.29	−0.48	−0.31
Deaths while on waiting list
UNOS	331	279	299	301	263	287	269	285	309
Model mean ($\overline{x}$)	323.66	311.00	315.20	322.26	295.00	309.66	303.13	279.15	295.84
Model standard deviation (s)	23.23	22.35	26.54	28.37	22.37	30.59	26.60	25.36	26.84
Difference (%)	−3.51	5.45	5.32	−3.87	16.25	8.54	−5.40	−5.88	−3.16
Number of patients on the waiting list
UNOS	2,551	2,417	2,466	2,712	2,904	2,847	3,063	3,332	3,400
Model mean ($\overline{x}$)	2504.23	2389.10	2224.40	2433.10	2565.80	2431.36	2606.36	2847.73	3044.06
Model standard deviation (s)	98.25	120.34	126.11	130.96	149.69	174.65	155.08	133.34	165.92
Difference (%)	−1.86	−1.16	−10.86	−11.46	−13.18	−17.09	−17.51	−17.00	−11.69
Transplants performed
UNOS	1,870	1,877	1,796	1,851	1,967	1,944	1,998	2,123	2,241
Model mean ($\overline{x}$)	1897.00	1944.50	2107.60	1968.03	2072.10	2080.10	2158.53	2295.76	2429.43
Model standard deviation (s)	36.81	42.30	42.61	49.22	52.61	48.17	43.62	45.58	55.49
Difference (%)	1.42	3.47	14.78	5.94	5.07	6.54	7.43	7.52	7.75
Delisted patients
UNOS	524	604	690	570	607	736	641	711	893
Model mean ($\overline{x}$)	520.43	609.26	694.96	569.33	598.26	740.23	640.66	710.16	890.80
Model standard deviation (s)	22.89	23.46	28.17	25.43	21.51	28.79	22.94	23.88	29.83
Difference (%)	−0.68	0.86	0.71	−0.11	−1.45	1.24	1.50	0.44	0.87

Note: UNOS = United Network for Organ Sharing. For the simulation model, mean ($\overline{x}$) and standard deviation (s) are the results of 30 replications.

Table 2.

P Values for t Test for Comparing Real Data and Simulation Outputs

Measure	New Patients Arrival	Diseased Donors Arrival	Deaths While on Waiting List	Number of Patients on the Waiting List	Transplants Performed	Delisted Patients
P value	0.58	0.99	0.10	0.14	0.07	0.99

Fairness Analysis

Fairness is extensively studied in resource allocation problems involving a central decision maker and multiple players where each player receives a utility based on the allocation chosen by the central decision maker. In this context, the utility of a patient could be her or his postlisting life expectancy or quality-adjusted life expectancy (one might also include perioperative pain and distress). The utilitarian principle implies that an efficient allocation is one that maximizes the sum of the expected utilities of the players, that is, postlisting life expectancy of the patient population.²² However, the decision maker may settle on the utility allocation, which incorporates fairness considerations. In this work, we considered two axiomatically justified notions of fairness: proportional fairness and max-min fairness.^23,24 The idea of max-min fairness is to prioritize the players that are the least well off, so as to ensure the highest minimum expected utility that each player derives.^25,26 Proportional fairness is the generalization of Nash solution where multiple players are involved.²⁷ In this fairness scheme, a transfer of resources is justified if the gainer utilities increase by a larger percentage than loser utilities decrease. That is, an allocation rule is proportionally fair if, compared to any other allocation rule, the aggregate proportional change is nonnegative.

Suppose there are $N$ players and $U_j$ denotes the utility of player $j$ and ${\mathrm{\omega }}_j\ge 0$ is a weight such that ${\displaystyle {\sum }_{j=1}^N{\mathrm{\omega }}_j}=1$. Note that since humans are equally precious, in the fairness analysis, we considered equal weights for all the patients (i.e., ${\mathrm{\omega }}_j=(1/N)$). Define

$$M_{\mathrm{\alpha }}(U,\mathrm{\omega })=\{\begin{array}{c}{\Pi }_{j=1}^N{U_j}^{{\mathrm{\omega }}_j};\mathrm{\alpha }=1\hfill \\ \hfill {\left({\sum }_{j=1}^N{\mathrm{\omega }}_j{U_j}^{1-\mathrm{\alpha }}\right)}^{\frac{1}{1-\mathrm{\alpha }}};\mathrm{\alpha }\ge 0,\mathrm{\alpha }\ne 1\hfill \end{array}$$

and let $\mathrm{\pi }$ denote an admissible policy. To find the fairest allocation, we considered a decision maker who seeks to find a policy that yields the maximum value for the expected value of fairness measure defined in (1), that is, a policy maker seeks a policy that maximizes the following quantity

$$v^{\mathrm{\pi }}(s_0)=E^{\mathrm{\pi }}\{M_{\mathrm{\alpha }}(U,\mathrm{\omega })|s_0\}$$

where $s_0$ is the initial patient population and expectation $E^{\mathrm{\pi }}\{·\}$ is taken over all randomness in the system. Let ${\mathrm{\pi }}^{*}$ be the policy that maximizes formulation (2). Computing ${\mathrm{\pi }}^{*}$ requires solving Bellman optimality equations, and since the state space is extremely huge (may increase exponentially), the current methods do not apply.²⁸ Thus, one needs to use approximate solutions by approximate dynamic programming or fluid scaling,²⁹ which is beyond the scope of this study.

However, the fairness analysis studied in this section only provides the fairness ranking among the policies and it reveals nothing about the fairness measure for the optimal fair policy.

In order to study the fairness in the heart allocation context, we considered a family of α-fairness that include both max-min and proportional fairness as special cases. In particular, α = 1 and α→∞ correspond to proportional and max-min fairness, respectively. Therefore, for a given allocation policy π and initial patient population $s_0$, we defined a metric ($v^{\mathrm{\pi }}(s_0)$), which measures the fairness of allocation policies based on the α-fairness concept, that is, assigns a numerical value to policy π. Then, an optimal α-fair policy can be found by searching over all possible allocation policies.

In our implementation, we considered postlisting life expectancy as the utility for each patient, defined as the expected life years that each patient gains from when she or he joins the waiting list, until she or he dies. In order to estimate $v^{\mathrm{\pi }}(s_0)$ for a given policy π, we created the initial patient population $s_0$ according to the waiting list distribution in 2006 and simulated the system until 2014. Recall that we generated the same patient population and donor heart for all allocation policies. For each patient in the system (those who were in the system and arrived through the entire horizon), we calculate the postlisting life expectancy as we know when she or he joined the system and when she or he died. A patient may die while waiting for transplant or after transplant. For patients who went under transplantation, after our simulation ends at 2014, we let the simulation of posttransplant patients continue until all died. For patients who are still alive at the end of simulation horizon, we let the simulation run until all die. This approach assumes that patients on the waiting list at the end of the simulation horizon do not go under transplantation. However, this assumption is not restrictive as this procedure 1) can easily incorporate the heart arrivals in the future and 2) holds for all policies; therefore, their rankings remain intact. We removed the patients delisted from the analysis as we could not locate historical data on their survival distribution. We estimated the expected values in formulation (2) by the Monte Carlo simulation, that is, we simulated the system and in each simulation recorded the total utility of the entire patient population and took an average over all runs. For each of the four considered policies, after simulating the policy, we calculated (2) for both cases α = 1 and α→∞. These values are reported in Table 4. Note that our simulation uses pre- and posttransplant Cox survival models to estimate the probability of death at each time period for patients on the waiting list and those on the posttransplant phase. We validated these models, which are the base for estimating postlisting life expectancies, by comparing our simulation results with those in real data (Tables 1-3).

Table 4.

Results of Fairness Comparison of Policies

Policy	Proportional Fairness Measure	Max-Min Fairness Measure
UNOS	2209.28	108.76
Policy I	2356.50	109.45
Policy II	2294.40	109.77
Policy III	1921.92	108.86

Note: UNOS = United Network for Organ Sharing. The proportional and max-min fairness measure columns indicate the values of $v^{\mathrm{\pi }}(s_0)$ defined in formulation (2) for α = 1 and α→∞, respectively. Note that a higher number implies a smaller gap from the optimal fair policy. We used life days as a metric for each individual’s utility.

Table 3.

Survival Rates of Patients Transplanted During 2006 to 2008

Survival	One-Year Survival Rate	Two-Year Survival Rate	Three-Year Survival Rate	Four-Year Survival Rate	Five-Year Survival Rate
UNOS reports	0.89	0.85	0.82	0.79	0.75
Model mean ($\overline{x}$)	0.93	0.88	0.84	0.80	0.75
Difference (%)	4.30	3.40	2.38	1.25	0.00

Note: UNOS = United Network for Organ Sharing.

Results

This section provides the numerical results of our analysis, including validation of the model and comparison of proposed allocation policies in terms of efficiency and fairness. Table 1 shows the result of the simulation model outcomes along with UNOS reports from the start of 2006 to the end of 2014. In particular, we reported the average and standard deviation of each output, as well as the percentage of relative difference between historical data and model outputs. The results of the simulation such as new patients listed, donor hearts, transplants performed, and delisted patients closely match those observed in historical data for almost all years. Specifically, we conducted statistical t tests (Table 2), and our results show that simulation outputs are not statistically different than real data. Our model slightly overestimated the pretransplant deaths and consequently underestimated the number of patients on the waiting list. All in all, the model mimics all the trends in different outcomes appropriately.

Table 3 shows 1- to 5-year posttransplant survival rates produced by simulation and UNOS data for patients transplanted between 2006 and 2014. The model predicts the posttransplant survival rates accurately, especially 3- to 5-year posttransplant survival rates.

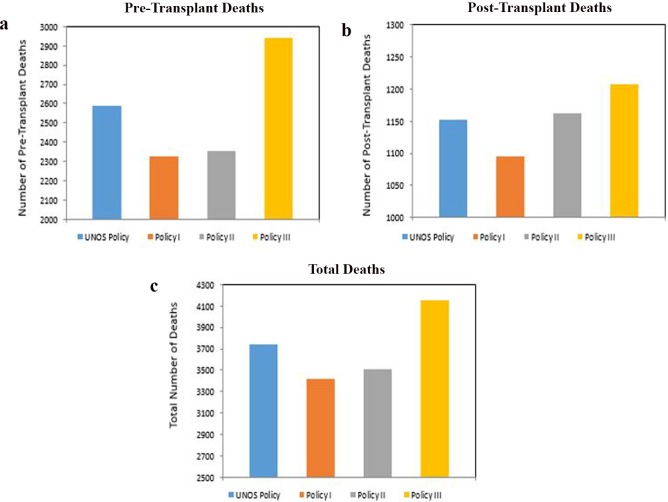
We compared the three policies described in the Allocation Policies section along with the UNOS practice in terms of efficiency and fairness. We considered a policy to be the most efficient if it achieves the least number of total deaths (pre- and posttransplant deaths), and closest to a fair (proportional or max-min) policy if it yields the highest value for the fairness measure defined in formulation (2). Figure 2 shows total patient deaths for each proposed policy from 2006 to 2014. Policy I, which combines Zones A, B, and C, outperforms other policies. In fact, Policy I reduced the expected number of deaths by 319. Also, policy II outperformed the UNOS policy. Moreover, the performance of Policy III was worse than the UNOS practice. The results indicate that prioritizing health status 1B over 1A and prioritizing waiting time are suboptimal.

Figure 2.

Comparison of pretransplant, posttransplant, and total number of deaths for the UNOS and three considered policies since 2006 to the end of 2014. (a) The number of deaths on waiting list during 2006 to 2014 across the four policies. (b) The number of deaths after transplant during 2006 to 2014. (c) The total number of deaths in the study period for each of the studied policies. Results of simulation showed that the total number of deaths for current UNOS policy is equal to 3,738. However, this number is equal to 3,419, 3,514, and 4,148 for the Policies I, II, and III, respectively. As can be seen, Policy I outperforms other policies.

Table 4 shows the results for $v^{\mathrm{\pi }}(s_0)$ to analyze the fairness of proposed policies. Intuitively speaking, a higher value of $v^{\pi }(s_0)$ for proportional (max-min) fairness indicates that the allocation policy $\mathrm{\pi }$ is closer to an optimal proportional (max-min) fair policy for the initial population $s_0$. In particular, in an optimal proportionally fair policy, the aggregate proportional change in postlisting life expectancy of patients compared to any other allocation rule is nonnegative. Also, an optimal max-min fair policy obtains the largest postlisting life expectancy for the patients who have the least life expectancy estimates, compared to any other allocation rule. Results show that Policy I is closer to an ideal proportional fair policy among others as it has the highest fairness measure. Also, our results show that in terms of proportional fairness, UNOS policy outperforms Policy III, which prioritizes based on waiting time. Moreover, our results show that all the proposed policies perform similarly in terms of max-min fairness.

Conclusion and Discussion

The problem of optimally allocating limited donor hearts to the patients on the waiting list is one of the top priorities in heart transplant management as the imbalance between supply and demand has increased over the past decade. Simulation models can help policy makers and medical professionals to analyze allocation rules without actually implementing them. We developed a stochastic simulation model of heart allocation system and validated it in several dimensions by comparing the model outcomes with historical data from 2006 to 2014. We also adapted two well-accepted fairness notions to develop a framework to analyze the fairness of allocation policies in the context of organ allocation. In addition to the UNOS allocation rule, we considered three additional policies: 1) one that combines Zones A, B, and C; 2) one that prioritizes status of 1B over 1A; and 3) one that prioritizes candidates based on waiting time. Our results showed that the policy that combines Zones A, B, and C could avert 319 total deaths (pre- and posttransplant deaths) and was closer to an ideal proportionally fair allocation policy. Hence, it seems that combining these priority zones and broadening the organ sharing area may result in more efficient and fair policies. Moreover, combining zones is easy to understand and straightforward to implement. Our results have a similar message with those observed for the Eurotransplant heart allocation simulation model, where international organ exchange is estimated to reduce waiting list mortality in different countries by 1.9% to 12.4%.¹¹ Studies on other organs also found that broadening the organ sharing area by multiple listing can significantly reduce the mortality rate.²² Our results for the fairness analyses revealed that proportional fairness may be of more interest to measure the fairness of organ allocation policies as the max-min fairness measure for different policies was not significantly different. Our results show that this is due to the fact that the postlisting expected life of the very sick patients does not significantly change by different policies.

Our results indicated that the simulation model produced outcomes close to historical data, which increases the confidence that the model can reasonably approximate the quantities of interest to transplant community. In particular, one can use this model to analyze the performance of other allocation policies and derive insights on how allocation policies change the waiting list population dynamics. However, this study has several limitations, and by addressing them, we can develop a more accurate decision-making tool to evaluate allocation rules.

First, although detailed data on patient and donor heart arrivals were available in the UNOS/SRTR data sets for each region, these data were not available for each transplant center or OPO. Therefore, we generated appropriate distributions for each region and assigned the OPO of a new patient or donor heart based on a uniform distribution. The validation results show that patient and heart arrivals closely match historical data. Second, since UNOS/SRTR data sets reported the frequency of health status change independent of other patient attributes, we constructed a Markov chain in the patient health status change module based only on health status and ignored other dependencies such as age, gender, and waiting time. The validation of this module indicated that the distributions produced by the model are statistically the same as observed data. Third, because detailed data for heart wastage was not available in UNOS/SRTR data sets, we adjusted the heart arrivals to compensate heart wastage. Fourth, we did not model the patient choice in accepting/rejecting the offered heart. However, adding such a feature to the model is straightforward upon availability of data. Fifth, we considered postlisting life expectancy in analyzing the fairness of policies and did not consider quality-adjusted life expectancy or cost. The cost component, which includes pre- and posttransplant care, may affect policy recommendations.