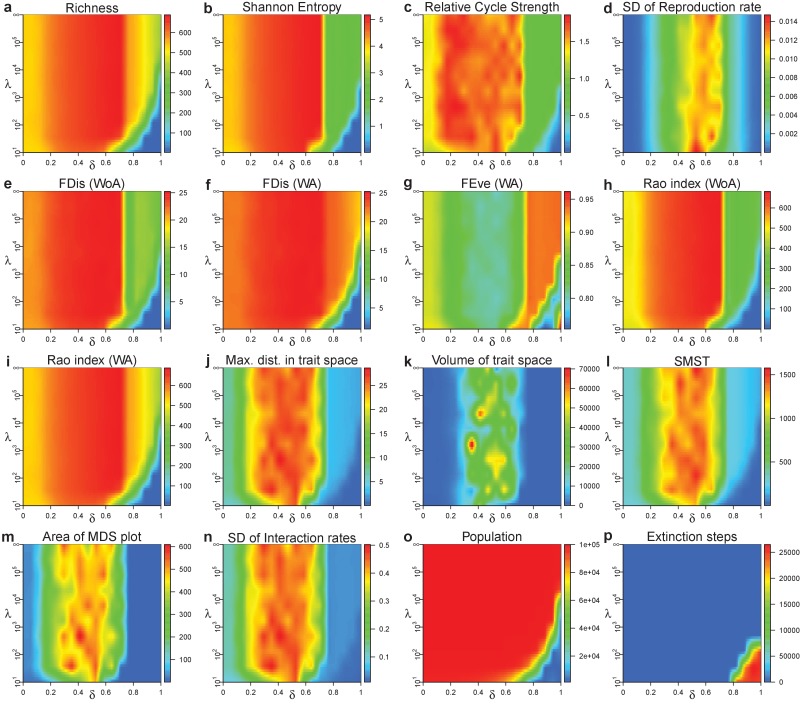
Appendix 1—figure 8. Diversity indexes used to compute the phase diagram of Figure 4 of the main text.

(a) Richness: number of different strains in community. (b) Shannon entropy: here a measure of evenness in strain population. (c) Relative strength of cycles of size three compared to random networks (see Appendix 1, Intransitive dominance cycles). (d) Standard deviation of replication $r$ as a measure of diversity in reproduction strategy. (e) Functional dispersion (FDis, without using the abundance vector): measures the mean distance of individual strains in trait space to their centroid. (f) Functional dispersion (FDis, using the abundance vector): measures the mean distance of individual strains (weighted by abundance vector) in trait space to their centroid. (g) Functional evenness (FEve, using the abundance vector): quantifies functional evenness and is higher when strains/species are spread homogeneously in trait space. When disruptive selection produces clusters of localized strains in trait space this index decreases. (h) Rao’s quadratic entropy (without using the abundance vector): measures mean functional distance between two randomly chosen individuals. (i) Rao’s quadratic entropy (using the abundance vector): measures mean functional distance between two randomly chosen individuals. (j) Maximum distance in trait space between strains. (k) Volume of trait space: calculated by multiplication of eigenvalues of factor analysis. (l) SMST (see Appendix 1, SMST and distribution of species and strains in trait space). (m) Area of MDS plot: calculated by multiplication of the two first eigenvalues of factor analysis. (n) Standard deviation of interaction terms. (o) Community population: number of individuals in community. (p) Number of mass extinction events over $5\times {10}^6$ generations. Each plot is the average of corresponding index over three simulations each over $5\times {10}^6$ generations. Simulations with $\mu =0.001$, $m=0.02$ and $N_s={10}^5$.