Individual preventive social distancing during an epidemic may have negative population-level outcomes

Abstract

The outbreak of an infectious disease in a human population can lead to individuals responding with preventive measures in an attempt to avoid getting infected. This leads to changes in contact patterns. However, as we show in this paper, rational behaviour at the individual level, such as social distancing from infectious contacts, may not always be beneficial for the population as a whole. We use epidemic network models to demonstrate the potential negative consequences at the population level. We take into account the social structure of the population through several network models. As the epidemic evolves, susceptible individuals may distance themselves from their infectious contacts. Some individuals replace their lost social connections by seeking new ties. If social distancing occurs at a high rate at the beginning of an epidemic, then this can prevent an outbreak from occurring. However, we show that moderate social distancing can worsen the disease outcome, both in the initial phase of an outbreak and the final epidemic size. Moreover, the same negative effect can arise in real-world networks. Our results suggest that one needs to be careful when targeting behavioural changes as they could potentially worsen the epidemic outcome. Furthermore, network structure crucially influences the way that individual-level measures impact the epidemic at the population level. These findings highlight the importance of careful analysis of preventive measures in epidemic models.

1. Introduction

Mathematical models for the spread of infections have been used successfully to increase understanding of how epidemics may propagate: what are the most important features to determine the initial epidemic growth, final epidemic size or endemic level? Mathematical models are also useful to evaluate the possible effects on epidemic dynamics of preventive measures. This can guide public health officials to decide what measures could be put in place to reduce or even stop spreading of a disease [1].

To prevent or control an epidemic, public health authorities may implement measures by, for example, isolating/treating detected infectious cases or starting a vaccination scheme, either before or during the outbreak [1]. In addition, individuals may take their own measures to prevent themselves from getting infected, e.g. by wearing face masks, taking hygienic measures such as hand washing, or by socially distancing themselves from infectious contacts. Such individual behaviour has been observed in, for example, the recent Ebola outbreak and the 2009 A/H1N1 epidemic [2–6].

In general, it is hard to predict the effect of preventive measures without using models to guide us. Epidemic dynamics are highly nonlinear and therefore preventive measures can lead to counterintuitive effects. Standard epidemic models assume human behaviour is not influenced by the epidemic and is constant over time. Although it is often recognized that humans do take preventive measures in the course of an epidemic, models that incorporate behavioural dynamics are generally much harder to analyse. Recently, such models have started to receive more attention, and important advances have been made to gain understanding of the effect of different behavioural changes on epidemic dynamics [7–10].

A crucial modelling ingredient is the contact pattern in the population as infection is transmitted through contacts between susceptible and infectious individuals. Owing to challenges in their analysis, the majority of models that consider behavioural responses to epidemic dynamics are relatively simple in modelling contact patterns [10]. Often the simplest assumption of homogeneous mixing, or some variant, is made. This assumption implies that any two individuals rarely meet more than once in a large population. To overcome the restriction of the lack of repeated contacts, network epidemic models have been proposed to model human contact patterns. This class of models have received much attention over the last 20 years or so [11,12]. In these models, individuals are socially connected in the network and infection is only possible along connections. Network models are also a natural way to incorporate heterogeneity in the number of connections that individuals in the population have. Throughout this paper, we refer to two individuals that are connected to each other as ‘neighbours’. Exactly what a neighbour is depends on the social structure under consideration, e.g. one may think of the neighbours as ‘colleagues’ in workplaces or ‘sexual partners’ in sexual networks.

In this paper, we study a network SIR (susceptible–infectious–recovered) epidemic with preventive social distancing. We consider the setting where susceptible individuals distance themselves from their neighbours who they find out are infectious, perhaps sometimes simply dropping such connections and other times, in their wish to maintain a certain number of social connections, by seeking new connections (which we refer to as ‘rewiring’). We study the impact of social distancing on model networks as well as real-world networks.

We show that rational preventive individual-level behaviour can have counterintuitive negative population-level consequences. From the perspective of an individual who distances him/herself from an infectious individual, this preventive behaviour is always rational in the sense that it decreases the risk of him/her getting infected during the epidemic outbreak (here ‘always’ means for all rewiring and dropping rates on all networks). If the social distancing occurs at a high enough rate at the beginning of an epidemic, then this can prevent an outbreak from occurring. In such cases, the population-level effect is obviously always positive. However, we also show that having individuals who rewire away from infectious neighbours and possibly replace them with new ties may be harmful for the community as a whole. Depending on the network structure of the population, social distancing may in fact increase the epidemic threshold parameter from below to above its threshold value, making a large outbreak possible where without social distancing it was not. We also show that social distancing can increase the final size of the epidemic. It is important to stress that these features do not hold for all networks. However, we show that there are real-world networks as well as model networks which exhibit these properties. It is difficult to characterize completely when such individual preventive behaviour is harmful, but it tends to happen more easily if: (i) the epidemic threshold parameter for an epidemic to take off (for the baseline setting without social distancing) is large, (ii) the network has many individuals with low degree and possibly other groups being highly interconnected and (iii) connections are more likely to be rewired than dropped. The theoretical findings of our study highlight the importance of taking preventive measures into account in epidemic models.

2. Model

2.1. SIR epidemic with social distancing on a network

We consider a population in which individuals are socially connected. Two individuals that are connected to each other are referred to as neighbours and contacts are only made between neighbours. The individuals and the connections between them together make up the network structure of the population. The stochastic SIR (susceptible-infectious-recovered) epidemic with social distancing on a network is as follows. Initially, usually one individual is infectious, we call this individual the index case, and all others in the population are susceptible (specific assumptions concerning the index case are given later). An individual that gets infected becomes infectious and remains so for an exponentially distributed time with mean 1/γ, then it becomes recovered and immune to further infection. During its infectious period, an individual transmits infection at a constant rate β independently to each susceptible neighbour. Moreover, a susceptible individual that has an infectious neighbour distances him/herself from this neighbour. The susceptible individual then either rewires the connection to an individual chosen uniformly at random from the population or drops the connection completely. We model this by a social distancing rate ω and a probability α to rewire rather than drop the connection. Whenever a social distancing event happens, the susceptible individual immediately choses a new neighbour uniformly at random from the entire population with probability α, and with the remaining probability 1 − α the susceptible individual simply drops the connection (so a susceptible individual rewires from an infectious neighbour at rate αω and drops the connection at rate (1 − α)ω). Dropping and rewiring events happen independently between all pairs of susceptible and infectious individuals. Note that the probability that a susceptible individual distances oneself from a given infectious neighbour before becoming infected or the neighbour recovering is ω/(β + ω + γ). For example, for a mean infectious period of 1/γ = 5 days and transmission rate β = 0.1 d⁻¹, the probability ω/(β + ω + γ) of social distancing of the susceptible individual before transmission or recovery of the infectious neighbour is 0.12 if ω = 0.04 d⁻¹ and 0.67 for ω = 0.60 d⁻¹. The epidemic continues until no infectious individuals remain.

Note that the preventive measure of social distancing is always beneficial from the individual perspective. Indeed, a susceptible individual that distances itself from an infectious neighbour avoids the risk of getting infected by that particular individual. In the case that it chooses to replace that social connection (rewiring), and that new neighbour is recovered (and immune), transmission can no longer occur through that connection. If the neighbour is susceptible, transmission through that connection could occur later on in the epidemic. If the neighbour is infectious, then all that has happened from an epidemic point of view is that one infectious neighbour is replaced by another one, and the risk of becoming infected is unchanged. Obviously, the most beneficial option from the point of view of avoiding getting infected is not to replace the connection (corresponding to α = 0 and ω > 0 in the model). At the population level, this means that there are fewer connections through which the epidemic can spread. Therefore, this extreme case of dropping connections is always beneficial from both the individual and population perspective. Consequently, provided infectives can recover (γ > 0), if most of the social distancing is done through dropping connections rather than rewiring them (small α) then this will also be beneficial for the population.

The epidemic with social distancing is studied on two network models as well as some real-world networks. The networks are described in §2.2. Our results in §3 involve several epidemiological measures for the beginning and the end of the epidemic, these concepts are introduced in §2.3.

2.2. The networks

2.2.1. Configuration network

The configuration model is a well-studied network, both within and without the context of epidemic models [13–15]. The network is constructed by first defining its degree distribution {p_d}_d^∞₌₀, where p_d is the probability that an individual has exactly d connections. In a population of size n, each of the n individuals picks a degree independently from {p_d} and attaches that many half-edges to itself. Half-edges are then paired completely at random and the corresponding individuals are connected in the network. By the way of this construction, some imperfections may arise, such as self-loops or multiple connections between some pairs of individuals. However, such imperfections become sparse in the network as the population size n → ∞ if the degree distribution has finite variance (see e.g. [16], theorem 3.1.2) and electronic supplementary material, section S5). Under such conditions the asymptotic n → ∞ results in our paper hold also if the network is conditioned to have no such imperfections [17]. Those asymptotic results are valid as approximations only for large populations. What constitute large depends on many factors but simulations indicate that usually the approximations are good for sizes in the low hundreds.

2.2.2. Clique network

The clique-network model [18] (also referred to as household-network model when the cliques are interpreted as households) has two types of connections: global network connections and clique connections. The global network structure is obtained through the configuration network with prescribed degree distribution {p_d}. On top of this, the community is partitioned into distinct units (cliques) of size three (see electronic supplementary material, section S2 for a discussion on allowing for variable clique sizes). The population can be partitioned into cliques by labelling all individuals from 1 to n, and letting the first three individuals make up clique 1, the next three individuals make up clique 2, and so on. In the final network, individual 1 is then connected to all individuals he/she is connected to from the construction of the configuration model together with individuals 2 and 3 from the clique construction, and similarly for the other individuals.

2.2.3. Real-world networks

The real-world networks for our studies are taken from the Stanford large network dataset collection [19] and SocioPatterns [20,21], where datasets for several different networks are freely available. We considered the ‘arXiv General Relativity collaboration network’ and the ‘Facebook social circles network’ from [19] and two ‘Infectious SocioPatterns’ networks from [20]. All networks are undirected. The arXiv General Relativity collaboration network describes scientific collaborations between authors that submitted papers to the arXiv in the General Relativity and Quantum Cosmology category. Edges between nodes represent two co-authors that have written a paper together. In the Facebook social circles network, nodes are survey participants of the social network website Facebook that were using a specific app. Edges between nodes represent the ‘circles’ or ‘friends lists’ of those participants. The Infectious SocioPatterns networks describe close-contact interactions between visitors of a Science Gallery exhibition in Dublin, where all contacts are aggregated over a day. Data were collected over a period of 69 days, we consider two representative networks for that period that we refer to as SG1 and SG2 [20,21]. The networks are described in more detail using summary statistics such as degree mean, median and variance, numbers of nodes and edges in electronic supplementary material, section S3.1. Moreover, additional summary statistics such as clustering coefficients are documented in [19,21].

2.3. Epidemiological quantities: threshold parameters, the probability of a major outbreak and final size

In general, the social distancing model is challenging to analyse mathematically (see [22] for analysis of the beginning of an epidemic on the configuration network). As the network structure depends on the epidemic dynamics, models very soon become intractable. Therefore, in the main text we present the heuristics of our analytical results and refer to the electronic supplementary material for the mathematical details. In §3, the main focus is on our findings from simulation studies. Here, we present the key epidemiological concepts that are used in §3.

For the beginning of the epidemic, in the configuration network model we use the basic reproduction number R₀ that has the interpretation as the expected number of secondary cases generated by one typical newly infected individual at the beginning of the epidemic. The number R₀ is a threshold parameter with threshold value one in the sense that, in the limit as the population size n → ∞ there is a positive probability of a major outbreak (one which infects a strictly positive fraction of the population as n → ∞) if R₀ > 1 and no major outbreak occurs if R₀ ≤ 1. Owing to stochastic effects, it is always possible that an epidemic dies out when introduced into a population with finite size n, even when R₀ > 1. Previous work ([22]; see electronic supplementary material, section S1.2) showed that the basic reproduction number R₀ for the epidemic on the configuration network with social distancing is given by

2.1

where μ_D and 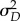are the mean and variance of the degree distribution {p_d} of the configuration network. Note that 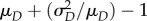is the expected number of susceptible neighbours of a typical newly infected individual in the early stages of an epidemic and β/(β + ω + γ) is the probability of transmitting to such a susceptible individual before he/she recovers or the neighbour drops the connection or rewires away.

Related to R₀ is the clique reproduction number R_* (also referred to as the household reproduction number when the cliques under consideration are households), which is more natural to consider when studying populations with a clique structure. Rather than considering a newly infected individual, one considers a newly infected clique as the unit of interest. The same threshold behaviour holds. The clique reproduction number R_* is derived in §3.2 and electronic supplementary material, section S2.1.

For an epidemic on both the configuration network and the clique network, as the population size n tends to infinity, the final fraction 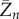of individuals that ever get infected converges in distribution to the random variable 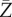with two-point distribution: 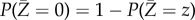. In the event of a major outbreak, the limiting final fraction of the population infected by the epidemic is z. In general, this constant z is only characterized implicitly, even for the simplest Markovian homogeneously mixing SIR epidemic model. We use the practical definition in our simulation studies in §3 that an epidemic outbreak is major if the final number of infected individuals is more than 10% of the total population size. We use the fraction of simulations resulting in major outbreaks according to this definition as an approximation for the probability of a major outbreak to occur. Furthermore, we set the mean infectious period 1/γ equal to 5 days as this lies in the typical range for many infectious diseases, such as rubella and polio. In our results presented below for the model networks, we investigate a range of ω-values starting at zero and becoming large enough that the threshold parameter (R₀ or R_*) is reduced below the critical value of one. For the real-world networks where the final size increases through social distancing, the range of ω-values is chosen such that the decrease in the average final size for large enough ω can also be observed, whereas for the other real-world networks the range of ω is chosen so that comparison between different networks can be made. More details on the simulation studies are provided in electronic supplementary material, section S5. We call the model without social distancing (ω = 0) the baseline model.

3. Results

3.1. The configuration network

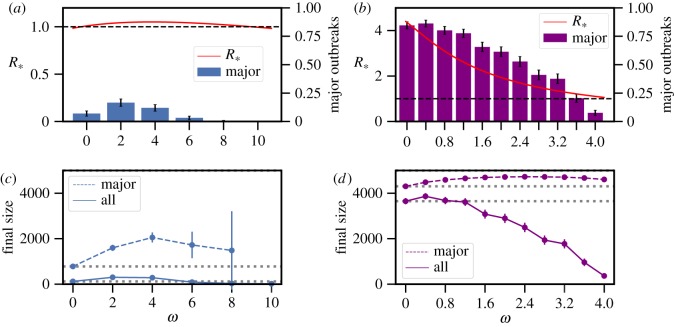
Social distancing in the configuration network is always beneficial at the beginning of an epidemic in the sense that it lowers R₀. This conclusion follows immediately from expression (2.1). In fact, social distancing can ensure that R₀ is reduced below the epidemic threshold value of one; see figure 1b for an example. At the beginning of an epidemic, from the point of view of a susceptible individual, social distancing from an infective neighbour ensures with high probability that he/she avoids infection during the early stages of an epidemic. Indeed, there are only few infectives in the population in that stage of the epidemic. This makes it unlikely for a susceptible individual who rewires to encounter another infectious individual at the beginning of the epidemic.

Figure 1.

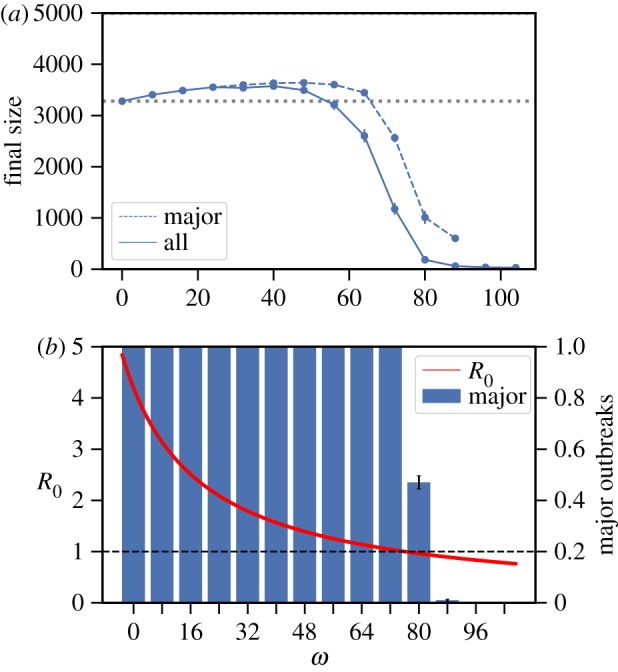
Social distancing can lead to an increase in the final size for the configuration network model. (a) Average final size (with 95% confidence intervals (CI) whenever large enough to be visible on the scales used in the plots) over all outbreaks (solid line) and restricted to major outbreaks (dashed line); the dotted horizontal line is at the final size when ω = 0, for reference. (b) R₀ as a function of social distancing rate ω (dashed black line at R₀ = 1 indicates the threshold value) and fraction of all outbreaks resulting in major outbreaks (with 95% CI). Model parameters are as follows. An individual in the population has degree d with d = 0,…, 10 with probability p_d = c/(d + 1), d = 0,…, 10 with c = 0.331 the normalization constant. Other parameter values are α = 0.9, β = 20 d⁻¹ and 1/γ = 5 days, total population size 5000, and each epidemic starts with 10 randomly chosen index cases. For each value of ω, 500 epidemics are simulated. (Online version in colour.)

However, social distancing need not be beneficial for the population as a whole. In fact, even though rewiring decreases R₀, it can still lead to an increase in the final size. To show analytically that the expected final size can increase with ω, we consider a very specific degree distribution, where individuals have either degree 0 or degree k, where k > 2, i.e. p₀ = 1 − p_k (proving things for more general degree distributions seems very hard). We analyse a related model that allows us to derive an asymptotic lower bound for the model of interest with strictly positive rewiring probability α > 0. In the related model, we consider an SI infection, i.e. set γ = 0. Then continuity arguments ensure that our results also hold for an SIR infection with γ > 0 small enough. Individuals act differently depending on their degree. A susceptible individual that tries to rewire to a randomly chosen individual v in the population will not do so (and simply drop the edge) if v is of degree k. If v is of degree 0, then rewiring takes place as usual, but v is prohibited from transmitting to other individuals. Therefore, the number of infections in the modified model is always less than in the original model (and is equal in the baseline model when there is no social distancing). For this modified model, we can derive an asymptotic (as n → ∞) lower bound for the final size that is increasing in ω for small ω > 0. It follows that, provided α > 0, for sufficiently small γ > 0, the final size of the model with social distancing is greater than that without social distancing for sufficiently small ω > 0. The details of the analysis are found in electronic supplementary material, section S1.3.

Rather than providing details for the analytical results for the final size here, we demonstrate the negative population level effects through simulation studies. We consider the social distancing model on a configuration network with heterogeneous degree distribution in figure 1. Parameter values are such that the basic reproduction number R₀ is large in the baseline setting and the majority of the social distancing is done through rewiring rather than dropping. The epidemic is started with 10 index cases (chosen uniformly at random from the population) in order to have most of the simulations resulting in major outbreaks. The number of index cases, unless sufficiently large, does not affect the final size of a major outbreak. We illustrate this fact by considering the scenario with one index case in electronic supplementary material, figure S1. Then the final size given a major outbreak increases as a function of social distancing as in figure 1, but the fraction of simulations resulting in a major outbreak is much smaller and consequently the average final size is decreasing. Additional results showing that social distancing can increase the final size for several other configuration network models are presented in electronic supplementary material, section S4. In particular, we consider different settings with a smaller rewiring probability α > 0.

Note that the fraction of epidemics that result in major outbreaks decreases with increasing social distancing rates (figure 1b). Despite this, the average final size of all outbreaks can still increase. Once the social distancing rate ω increases to a level such that the basic reproduction number drops below the epidemic threshold value of one (figure 1b), mostly minor outbreaks will occur. Finally, we note that deviations from the average final size are generally small (also compared to the total population size of 5000), especially when conditioning on the occurrence of a major outbreak.

3.2. The clique network

In the clique network, individual preventive social distancing can have a negative population-level effect already at the beginning of an epidemic. To demonstrate this, we consider R_* for the clique-network model. The clique reproduction number R_* is derived by differentiating between two types of newly infected cliques. A newly infected clique at first consists of one newly infected individual while the remaining clique members are susceptible. The two types are determined by the way the newly infected individual u* was infected: (i) u* was infected by a global neighbour (i.e. outside his/her own clique) that it had already before the start of the epidemic or (ii) u* was infected by a global neighbour that it acquired through a social distancing event during the epidemic. The clique reproduction number is the dominant eigenvalue of the 2 × 2 matrix (K_ij)_{i,j = 1,2}, where K_ij is the expected number of cliques of type j generated by one newly infected clique of type i. Details of the derivation of the K_ij are found in electronic supplementary material, section S2.1. We find an explicit expression for R_* that we can analyse as a function of social distancing ω and rewiring probability α for different degree distributions (see electronic supplementary material, section S2.2). We illustrate these analytical results with numerical examples in figure 2 for fixed rewiring probability α = 0.9 (but note that there is generally a range for α for which negative population-level effects can occur, depending on the network under consideration and other model parameter values; see electronic supplementary material, section S4).

Figure 2.

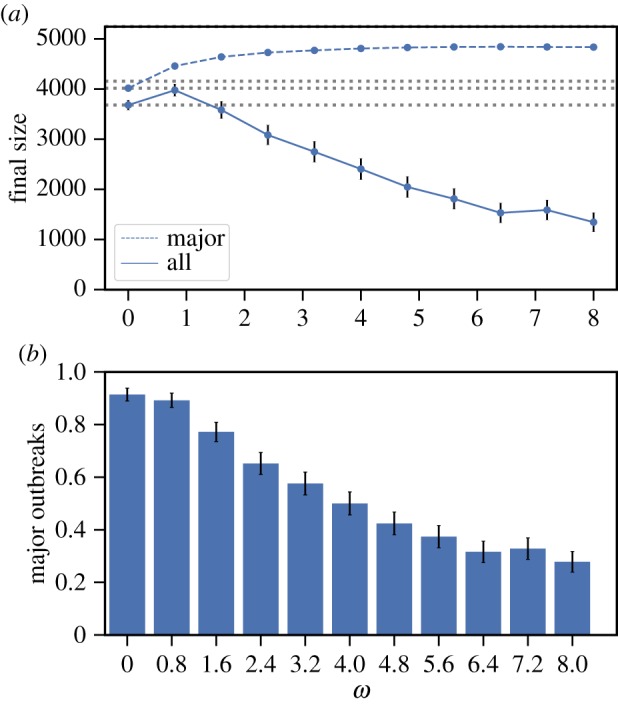
The effect of social distancing on the epidemic threshold parameter R_* and the final size. The fraction of epidemics resulting in major outbreaks (with 95% CI whenever large enough to be visible on the scales used in the plots) and R_* for (a) mean infectious period 1/γ = 5 days, β = 20 d⁻¹ and two-point degree distribution with 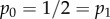and (b) mean infectious period 1/γ = 5 days, β = 2 d⁻¹ and two-point degree distribution with 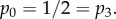Average final size with (dashed) and without (solid) conditioning on a major outbreak (with 95% CI) corresponding to (c) scenario A (d) scenario B; dotted horizontal lines are for comparison with the size at ω = 0. Other parameter values are as follows: cliques have size 3, the population size is 5000 and α = 0.9. Each epidemic is initiated with one randomly chosen infected individual and for each value of ω, 500 epidemics are simulated. (Online version in colour.)

As can be seen in figure 2a, R_* can increase as a function of the social distancing rate ω. In particular, social distancing can move the epidemic threshold R_* from below to above its threshold value of one. In other words, individual preventive measures that are beneficial at the individual level can cause a major outbreak to become possible while without the preventive measures this is not possible. However, this depends heavily on the precise network structure. In figure 2b, the degree distribution is chosen such that R_* decreases for all social distancing rates. See electronic supplementary material, section S2 for more details and examples of the dependence of R_* on social distancing. Note that R_* will eventually decrease for large enough social distancing rates as can be seen in figure 2a.

In settings where social distancing pushes R_* from below to above the threshold for an epidemic to occur, the effect of social distancing on the final size is large (figure 2c). Moreover, even in settings where social distancing reduces R_*, the final size can initially increase when social distancing is introduced into the model (figure 2d).

3.3. Application to real-world networks

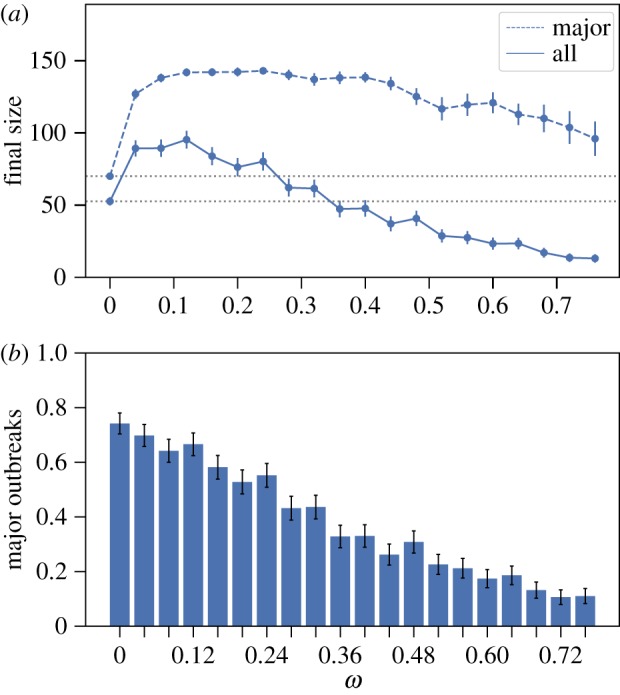
We consider four real-world networks: the arXiv General Relativity collaboration network and Facebook social circles network, taken from [19], and two Science Gallery networks that we call SG1 and SG2, taken from [20,21]. We simulate SIR epidemics with social distancing on these real-world networks (see electronic supplementary material, section S3.1 for details). In figures 3 and 4, we demonstrate that social distancing can have a negative effect at the population level by increasing the final size in the collaboration network and the SG1 network.

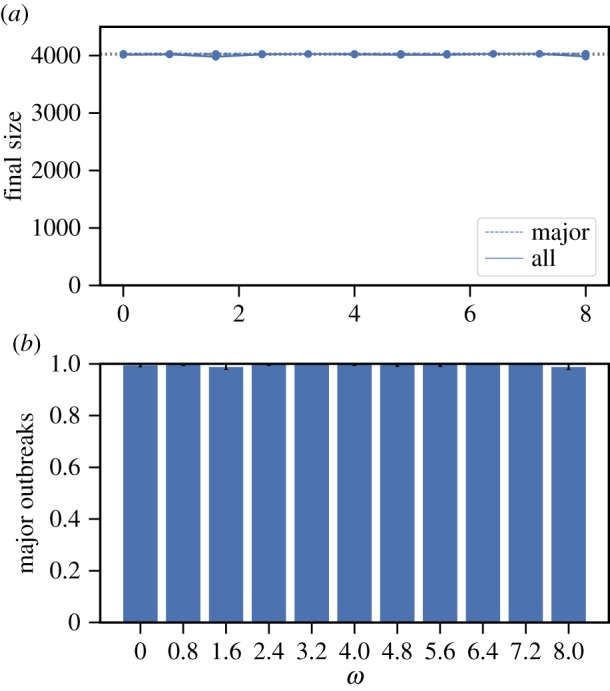
Figure 3.

Social distancing in the arXiv General Relativity collaboration network. (a) The average final size with (dashed) and without (solid) conditioning on a major outbreak (with 95% CI whenever large enough to be visible on the scales used in the plots); dotted horizontal lines are for the size of the giant component (top) and comparison with the size at ω = 0 (bottom two). (b) Fraction of all outbreaks that resulted in major outbreaks (with 95%). Model parameter values are: mean infectious period 1/γ = 5 days, β = 2 d^–1 and α = 0.9. For each value of ω, 500 epidemics are simulated. The index case is chosen uniformly at random from the sub-population of individuals that has median degree and are part of the largest connected component of the network. (Online version in colour.)

Figure 4.

Social distancing in the SG1. (a) The average final size over all outbreaks (solid) and conditioning on major outbreaks (dashed) (with 95% CI whenever large enough to be visible on the scales used in the plots); dotted horizontal lines are for the size of the network (top) and comparison with the size at ω = 0 (bottom two). (b) Fraction of all outbreaks that resulted in major outbreaks (with 95% CI). Model parameter values are: mean infectious period 1/γ = 5 days, β = 0.1 d^–1 and α = 0.9. For each value of ω, 500 epidemics are simulated. The index case is randomly chosen from the population that has median degree. (Online version in colour.)

Next, we consider the Facebook social circles network and the SG2 network in figures 5 and 6. These two networks serve to demonstrate that the precise network structure plays a crucial role for the effect that social distancing can have on the final size. For the Facebook social circles in figure 5, we find that if we restrict to only the major outbreaks, then a modest increase in the final size can be observed when compared to the baseline setting. On the other hand, the average final size is more or less unaffected by social distancing for sufficiently small social distancing rates. This can be explained by the network structure of the underlying population. As all individuals are part of the same connected component that contains many connections, i.e. all individuals are (indirectly) connected to each other, modest social distancing rates will not change the network structure in a way that significantly alters transmission patterns. Furthermore, for the SG2 network in figure 6, we find a slight increase in the final size for small social distancing rates but in general social distancing decreases the average final size compared with the baseline setting. Although also this network consists of one connected component, the relative number of connections is much smaller when compared with the Facebook social circles network (see electronic supplementary material, section S3.1 for network summary statistics).

Figure 5.

Social distancing in the facebook social circles network. (a) The average final size over all outbreaks (solid) and conditioning on major outbreaks (dashed) (with 95% CI whenever large enough to be visible on the scales used in the plots); dotted horizontal lines are for the size of the network (top) and comparison with the size at ω = 0 (bottom two). (b) Fraction of all outbreaks that resulted in major outbreaks (with 95% CI). Model parameter values are: mean infectious period 1/γ = 5 days, β = 2 d^–1 and α = 0.9. For each value of ω, 500 epidemics are simulated. The index case is randomly chosen from the population that has median degree. (Online version in colour.)

Figure 6.

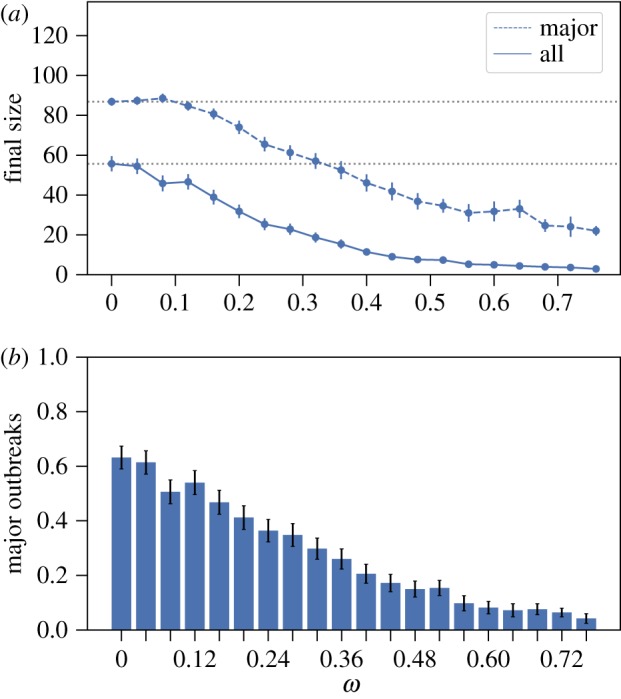
Social distancing in the SG2 network with randomly chosen index case with median degree. (a) The average final size over all outbreaks (solid) and conditioning on major outbreaks (dashed) (with 95% CI whenever large enough to be visible on the scales used in the plots); dotted horizontal lines are for the size of the network (top) and comparison with the size at ω = 0 (bottom two). (b) Fraction of all outbreaks that resulted in major outbreaks (with 95% CI). Model parameter values are: mean infectious period 1/γ = 5 days, β = 0.1 d⁻¹ and α = 0.9. For each value of ω, 500 epidemics are simulated. The index case is randomly chosen from the population that has median degree. (Online version in colour.)

In electronic supplementary material, section S4 additional scenarios for smaller probabilities α for the real-world networks are considered. We find that negative population-level effects can occur for arXiv General Relativity collaboration network and SG1 for a wider range of α-values while α has minor effects on the final size on the Facebook social circles network, and decreasing α leads to smaller final sizes on the SG2 network.

4. Conclusion and discussion

In the event of an epidemic outbreak in a population, individuals may take preventive measures by changing their contact patterns. Individuals may try to avoid infection by social distancing from infectious contacts. If this is done at a sufficiently high social distancing rate, then it can have a positive population level effect by bringing the reproduction number for an epidemic to take off below the threshold value of one. On the other hand, while preventive social distancing at moderate rates is always rational at the individual level, it may be harmful at the population level. In particular, preventive social distancing can increase the final epidemic size at the population level and thus have negative effects for the community at large. We demonstrated this counterintuitive result by means of different epidemic network models, as well as simulating epidemics with social distancing on existing real-world networks. Similar conclusions in terms of behavioural changes at the individual level and its population-level consequences have been drawn in [23,24] for different behavioural change models. Both [23,24] considered changes in human mobility patterns in the event of an epidemic and its consequences for the geographical spread. Using a metapopulation model, they illustrated that individual preventive measures in mobility patterns can lead to epidemic spread in new locations, although their invasion thresholds are always increasing [23] or even independent [24] of the behavioural changes, which is quite different from the dependence on social distancing of the threshold parameters R₀ and R_* in our models.

Whether or not social distancing of susceptible individuals from their infectious contacts will actually have negative epidemic outcomes depends strongly on the social network structure of the population. We demonstrated that social distancing can have different effects in the initial stages of the epidemic compared to the overall epidemic outbreak size. We considered the spread of an SIR epidemic on the clique-network model and the configuration network model. We showed that social distancing can have negative effects for the community by (i) increasing the epidemic threshold parameter R_* from below to above the threshold value of one in clique-networks with high clustering and (ii) by increasing the final size. Point (ii) for the final size was shown in (a) configuration networks with heterogeneous degree distribution, (b) clique-networks and (c) two real-world networks.

In general, in the baseline setting that an epidemic outbreak may occur when no preventive measures are taken, social distancing can always have beneficial effects provided that the rate of social distancing is sufficiently large (e.g. figure 3a). Indeed, sufficiently large social distancing rates can prevent an epidemic from taking off by reducing the epidemic threshold parameter from above to below its threshold value. In such cases, social distancing ensures that only a small number of individuals get infected by the epidemic, while in the baseline setting a significant fraction of the population may be infected.

Whereas social distancing never increases ones own risk of getting infected in our model, through rewiring, it can increase the risk for other individuals, e.g. by connecting to individuals that were previously not (so heavily) exposed to the epidemic. How and whether or not social distancing affects the population-level epidemic outcome depend on a variety of factors. Most notably, the network structure plays an important role (e.g. Figure 2). While it was not our aim to investigate models for specific diseases, we have chosen parameter values (e.g. 1/γ = 5 days and R₀ = 4.5 in the baseline model for figure 1) which are relevant for many infectious diseases. For example mumps, rubella and polio have estimated basic reproduction numbers around five and infectious periods are typically in the range of a few days to weeks. Note that we consider an infectious period that is exponentially distributed. The memoryless property of the exponential distribution ensures that social distancing is always beneficial at the individual level. Relaxing this assumption could potentially lead to different effects for the individual and/or the population level. This is an interesting extension to investigate in future work for which the current framework provides an excellent starting point. Furthermore, social distancing with larger values of α can more easily lead to negative effects at the population level. Exactly what constitutes sufficiently large α to realize this effect depends on the precise setting that one considers (e.g. for the clique network model with a Poisson degree distribution having mean 1 this occurs with R_* for all 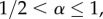while for the same model with degree distribution 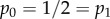the range of α is larger at 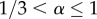; see also electronic supplementary material, sections S1.3, S2.2 and S4). These negative population-level effects also seem to arise more easily when the threshold parameter (R₀ or R_*) is high and the community has many individuals with low degrees and/or the community has highly connected cliques. In such cases, rewiring may introduce or increase connections to otherwise relatively isolated individuals. In this way, the smaller chance of the individual who takes preventive measures getting infected is outweighed by the increased risk of transmission to a larger part of the population in the event of infection.

The main point of the paper is to show, mathematically in the electronic supplementary material and by means of simulations in the main text, that social distancing may for some networks actually increase the total number of infected individuals at the end of the outbreak. Social distancing could also affect other features of an outbreak, such as the size and time of the peak and the duration of the outbreak. To show any mathematical results for such finer details of the outbreak appears to be very hard but can of course be addressed by means of simulations. A thorough study, preferably accompanied by some mathematical results, remains to be done.

Although it is generally recognized that individual preventive measures are often taken once awareness of an epidemic is in place, it is not well understood how to model changes in individual behaviour. Here, we considered the effect of social distancing on an epidemic. We modelled this on a contact network by assuming that susceptible individuals distance themselves from infectious contacts, allowing for both dropping of connections and replacement with new contacts in the desire to sustain a certain number of social contacts. Social behaviour is far more complex than our social distancing model, and many behavioural changes will depend on the epidemic and population under consideration. For example, an important factor is risk perception. In the case of severe diseases, one can imagine that susceptible individuals will more likely drop connections rather than rewire them to other individuals in the population. There might be heterogeneity in preventive measures taken; some individuals might be willing to take more risks than others or have a stronger inclination to maintain a certain number of connections, e.g. for sexually transmitted infections (STIs) one can often distinguish between groups with distinctively different levels of sexual activity. How such structures influence epidemic outcomes is likely to depend strongly on assumptions made on, e.g. mixing between risk groups (how assortative mixing is and whether individuals have the same assortative behaviour when rewiring to other individuals).

In terms of different types of connections, another interesting extension is to distinguish between behavioural changes within and between cliques. If cliques represent, e.g. households, then one can imagine that susceptible individuals may drop connections to infectious individuals outside the household and intensify connections within the household instead. While the current study focuses on preventive behavioural changes of susceptible individuals, one could also consider behavioural changes of infectious individuals, e.g. isolation, either self-imposed or implemented by public health authorities. Such measures regarding infectious individuals would generally not have the negative population effects as seen with social distancing of susceptible individuals, though see [25] which shows that replacing individuals with essential societal roles, such as health workers, when they are detected as being infectious, by susceptible individuals can accelerate disease transmission.

Note that we assume that the network structure of the population is static in the absence of disease. Depending on the disease of interest it would be interesting to consider a network that is dynamic also in the absence of infection, as would be appropriate for STIs such as HIV to incorporate partner separation and formation over time. Superimposed on the dynamic network are then the dynamics that follow from social distancing (or other preventive measures). These are just a few important ways to modify and extend the social distancing model that we consider. As we find counterintuitive results already in the current model with relatively simple social distancing rules, it is difficult to understand how such extensions impact the epidemic, and certainly it would be interesting to investigate that in future work. Such extensions could then help to gain insights into real-world transmission dynamics in specific populations that might display some form of preventive measures that is in line with the simple social distancing model of this study. In order to relate preventive measures to real-world epidemics one would preferably be guided by disease-specific network and behavioural data (see e.g. [10] for references to studies considering behavioural changes during the course of an epidemic for specific diseases and populations).

However, the aim of our paper is to show, in a theoretical context, that rational individual-level preventive measures can have counterintuitive consequences for the population-level. Public health interventions that aim at changing individual behaviour through social distancing could have adverse consequences, for example, school closures could reduce social contacts between children in the school classes but may (partly) be replaced by social contacts outside of school. But similarly, these measures could be beneficial for the population. As our results show, it is not necessarily straightforward what effects such behaviour may have at the population level, where much may depend on the disease and population under consideration. These findings highlight the importance of understanding the properties of disease-specific contact networks and modelling individual-level behavioural changes in response to an epidemic to understand infectious disease dynamics.

Data accessibility

This article does not contain any additional data.

Authors' contributions

K.Y.L., F.B., D.S. and T.B. designed and performed research; K.Y.L. and T.B. analysed data; F.B. and D.S. advised on analysis and interpretation; K.Y.L. and T.B. wrote the manuscript; and F.B. and D.S. contributed to writing the manuscript.

Competing interests

We declare we have no competing interests.

Funding

This work was partially supported by a grant from the Simons Foundation and was carried out as a result of the authors' visit to the Isaac Newton Institute for Mathematical Sciences during the programme Theoretical Foundations for Statistical Network Analysis in 2016 (EPSRC grant no. EP/K032208/1). T.B. and K.Y.L. are supported by the Swedish Research Council (VR) grant no. 2015-050153. This work was also supported by a grant from the Knut and Alice Wallenberg Foundation, which enabled F.B. to be a guest professor at the Department of Mathematics, Stockholm University.