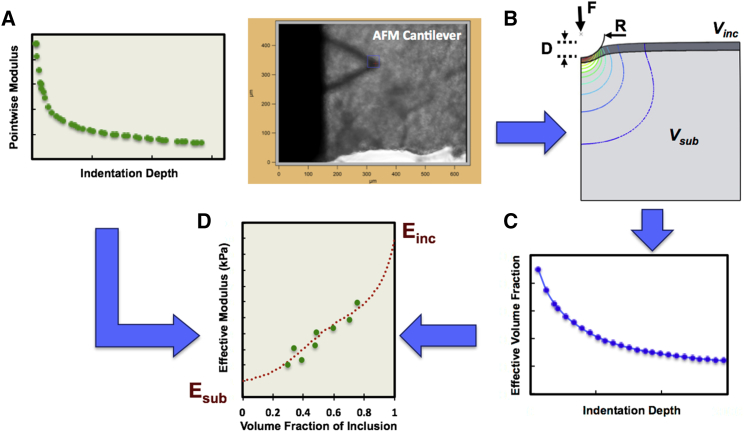
Figure 1.

Hybrid Eshelby Decomposition (HED) method. Starting with experimental AFM indentation data on a layered sample, (A) depth-dependent pointwise moduli confirming a mechanically heterogeneous sample were calculated. (B) An FEM model (e.g., using Abaqus) simulated an AFM indentation response for the given layered sample geometry and AFM probe tip dimensions using arbitrary elastic properties of the simulated sample. (C) The effective volume fraction of the layered inclusion versus indentation depth (i.e., master curve) was estimated for the given sample geometry based on modified Eshelby homogenization theory applied to FEM results. (D) The results of steps (A) and (C) were combined to plot pointwise modulus versus effective volume fraction at matched depths, and least-squares minimization (e.g., in MATLAB) was used to fit this data using modified Eshelby model for finite inclusions; assigning a Poisson ratio (ν = 0.49), the fitting procedure yields values of elastic modulus for the substrate and layered inclusion (E_sub and E_inc, respectively). To see this figure in color, go online.