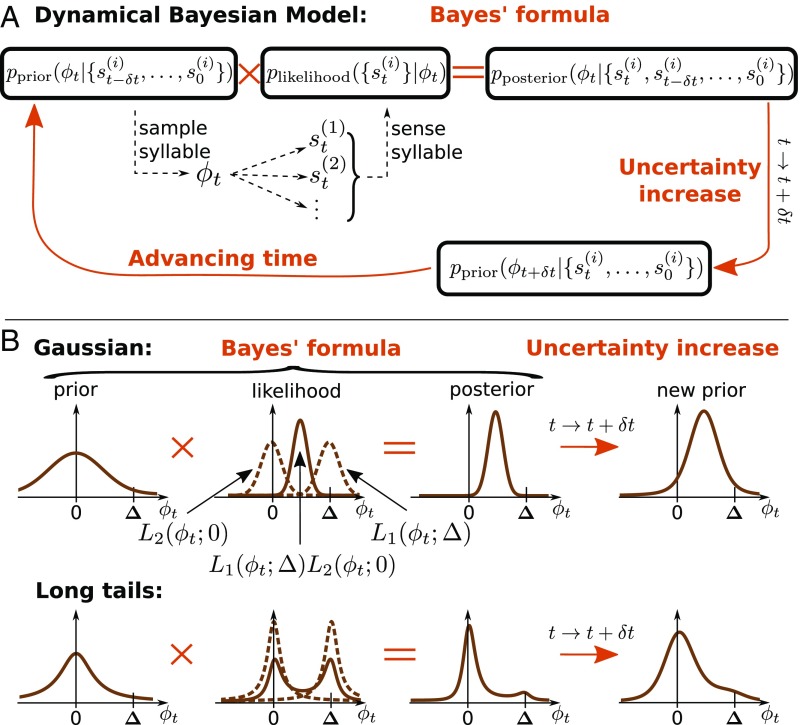
Fig. 1.

The dynamical Bayesian model (Bayesian filter). (A) A Bayesian filter consists of the recursive application of two general steps (35): (i) an observation update, which corresponds to novel sensory input and updates the underlying probability distribution of plausible motor commands using Bayes’ formula, and (ii) a time evolution update, which denotes the temporal propagation and corresponds to uncertainty increasing with time (main text); here the probability distribution is updated by convolution with a propagator. These two steps are repeated for each new piece of sensory data in a recursive loop. (B) Example distributions for the entire procedure in two scenarios: Gaussian (Top) and heavy-tailed (Bottom) distributions. The x axis, ${\varphi }_t$, represents the motor command which results in a specific pitch sung by the bird. The outcome of this motor command is then measured by two different sensory modalities, represented by ${\left\{s_t^{\left(i\right)}\right\}}_{i=\mathrm{1,2}}$, with corresponding likelihood functions $L_1\left({\varphi }_t;\mathrm{\Delta }\right)$ and $L_2\left({\varphi }_t;0\right)$, respectively. The $-\mathrm{\Delta }$ shift for modality 1 is induced by the experimentalist, which results in the animal compensating its pitch toward $+\mathrm{\Delta }$. Dashed brown lines represent the individual likelihood functions from the individual modalities, and the solid lines represent their product, which signals how likely it is that the correct motor command corresponds to ${\varphi }_t$. Heavy-tailed distributions can produce a bimodal likelihood, which, multiplied by the prior, suppresses large-error signals. In contrast, Gaussian likelihoods are unimodal and result in greater compensatory changes in behavior.