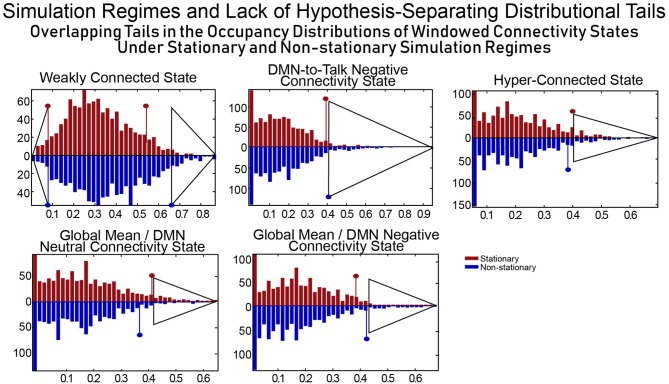
Figure 11.

For a combination of null model and test metric to allow for meaningful inferences, the null model should exhibit evidence of the phenomenon being investigated (and believed to be captured through the test metric) extremely rarely. SCC Gaussians arguably present evidence of FRBD as ubiquitously as the real fMRI data does. It is also not clear a priori that tail phenomena in SCC Gaussians should have an especially strong association to FRBD rather than, for example, to motion artifacts or measurement noise. Moreover, the measures evaluated on a null model are only helpful in identifying behavior of interest if the distributional tails of the measure do not overlap with those of the same measure evaluated on a model that violates assumptions of the original null hypothesis. The upper tails of the distributions of occupancy rates on the windowed connectivity states from SCC Gaussians (red) and the SS Non-stationary simulation regime (blue) have substantial overlap (semi-transparent gray triangles indicate the overlapping part of the tails for each state). Insufficient clarity on the unique, distinguishing features of the phenomenon being studied and of the models/measures being employed neutralizes the measure's role in hypothesis testing as the same observation can then present significant evidence against multiple, mutually contradictory null hypotheses. In terms of occupancy rates of windowed connectivity states, we see here that a newly scanned subject who spends 65% of their time in state 2 exhibits significant evidence against one statistically stationary null hypothesis and also against an explicitly non-stationary null hypothesis.