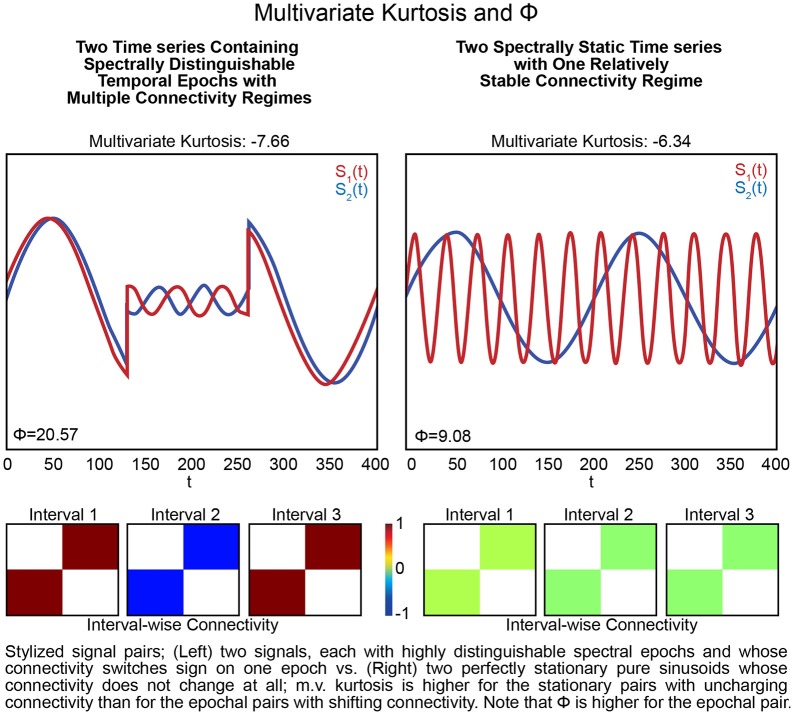
Figure 6.

Stylized signal pairs; (Left) two signals, each with highly distinguishable spectral epochs and whose connectivity switches sign on one epoch vs. (Right) two perfectly stationary pure sinusoids whose connectivity does not change at all; m.v. kurtosis is higher for the stationary pairs with unchanging connectivity than for the pairs with shifting connectivity. Note that Φ is higher for the pair that includes epochs. Excess multivariate kurtosis indicates multivariate super-Gaussianity (and is not particularly useful for indicating functionally relevant dynamics). Multivariate kurtosis (transformed via Equation 4 from the Technical Supplement) is assumed to be distributed, assuming multivariate Gaussianity on the part of the random vector, as a multivariate standard normal random variable) on both stylized multivariate examples. The first (Left) features two signals that each exhibit highly distinguishable spectral epochs and whose correlative behavior is also dynamic: they are perfectly correlated, then perfectly anti-correlated, then again perfectly correlated. This is a very dynamic context but not only presents negative multivariate kurtosis, its kurtosis value is even more negative than the second example (Right) that features two spectrally unchanging signals whose mutual correlations are consistently zero. The multivariate measure $\tilde{\Phi }$ is twice as large in the dynamic example (Left) compared to the static example (Right).