Estimating Individualized Treatment Rules for Ordinal Treatments

Summary

Precision medicine is an emerging scientific topic for disease treatment and prevention that takes into account individual patient characteristics. It is an important direction for clinical research, and many statistical methods have been proposed recently. One of the primary goals of precision medicine is to obtain an optimal individual treatment rule (ITR), which can help make decisions on treatment selection according to each patient’s specific characteristics. Recently, outcome weighted learning (OWL) has been proposed to estimate such an optimal ITR in a binary treatment setting by maximizing the expected clinical outcome. However, for ordinal treatment settings, such as individualized dose finding, it is unclear how to use OWL. In this paper, we propose a new technique for estimating ITR with ordinal treatments. In particular, we propose a data duplication technique with a piecewise convex loss function. We establish Fisher consistency for the resulting estimated ITR under certain conditions, and obtain the convergence and risk bound properties. Simulated examples and an application to a dataset from a type 2 diabetes mellitus observational study demonstrate the highly competitive performance of the proposed method compared to existing alternatives.

1 Introduction

In clinical research, precision medicine is a medical paradigm that promotes personalized health care to individual patients. Its recent development originates from the fact that treatment effects can vary widely from subject to subject due to individual level heterogeneity. For example, Ellsworth et al. (2010) found that women whose CYP2D6 gene has a certain mutation are not able to metabolize Tamoxifen efficiently, and this makes them an improper target group for this therapy. In this way, one of the primary goals for precision medicine is to establish rules so that patients’ characteristics can be used directly to find optimal treatments (Mancinelli et al., 2000). Recent literature indicates that statistical machine learning tools can be useful in building such rules. However, the primary focus has been on the binary treatment case, and the ordinal setting has not been fully explored. Ordinal treatments are commonly seen in practice. For example, some drugs for the same disease can be ranked by their medicinal strengths and multiple doses of the same treatment can be ranked by the dose level. However, the dose-response relationship is usually discussed from a population perspective in practice (Robins et al., 2008). In precision medicine, it is desirable to pursue the dose level that is best suited for each individual patient. In this paper, we develop a statistical learning model which can properly handle optimal treatment detection for both binary and ordinal treatment scenarios.

Various quantitative methods have been proposed in the statistical learning literature to estimate ITRs. For example, one group of methods aims to construct interpretable results by using tree-based methods to explore heterogeneous treatment effects (Su et al., 2009; Laber and Zhao, 2015). Another group of methods focuses on establishing a scoring system to evaluate patients’ benefits from certain treatments (Zhao et al., 2013). As an alternative, Qian and Murphy (2011) proposed a value function of the average reward that patients receive from their assigned treatments so that the rule discovery process is transformed into an optimization problem. Zhang et al. (2012) developed inverse probabilities for treatment weights to robustly estimate such value functions, and Zhao et al. (2012) proposed outcome weighted learning (OWL) to transform the rule detection problem into a weighted classification problem. In particular, the OWL approach uses a hinge loss function to replace the original 0–1 loss function in Qian and Murphy (2011), and thus the corresponding computation becomes feasible. Recently, Chen et al. (2016) adjusted OWL to the case of continuous doses to find the best dose.

Although Zhao et al. (2012) proposed an important idea on how the ITR can be estimated, there are still some challenges in practice. The first challenge is that OWL’s ITR estimate might be suboptimal when some patient rewards are less than zero. In this setting, a global minimizer of the loss function may not be obtainable since the objective function is no longer convex. If one chooses to manually shift all of the rewards to be positive, the estimated ITR tends to retain what is actually assigned (Zhou et al., 2017). To alleviate this problem, Zhou et al. (2017) recently proposed residual weighted learning. However, their resulting object function is non-convex, and consequently, global minimization cannot be guaranteed.

When we have multiple ordinal treatments, it would be useful to extend the objective function of OWL to solve the ITR estimation problem. Under this setting, direct extensions of binary OWL may not work well because it ignores how different the actual assigned treatment is from the optimal treatment. This can lead to information loss. In the literature of standard ordinal classification, one idea in statistical learning is the data duplication strategy introduced by Cardoso and Pinto da Costa (2007). This strategy borrows the idea from proportional odds cumulative logistic regression, which restricts the estimated boundaries not to cross with each other. Furthermore, the ordinal response is relabeled as a binary variable and duplicated in the covariate data to generate a higher dimensional sample space. Then, an all-at-once model is fitted in the transformed sample space to produce a corresponding ranking rule for the original response. Although such data duplication methods are shown to be effective in solving complex ordinal classification problems, it remains unclear how this idea can be utilized in OWL to help find the optimal ITR among multiple ordinal treatments.

In this paper, we propose a new method called generalized outcome weighted learning (GOWL). Specifically, our first contribution is to create a new objective function for ITR estimation based on the value function definition in Qian and Murphy (2011) by making use of the data duplication idea. We then formulate the optimal ordinal treatment rule detection problem into an aggregation of several optimal binary treatment rule detection subproblems. Furthermore, considering that each subproblem corresponds to a level of the ordinal treatment, we prevent estimated decision boundaries of the subproblems from intersecting with each other to circumvent contradictory results. The second contribution of the paper is to modify the loss function in Zhao et al. (2012) to maintain convexity regardless of whether the value of the reward is positive or negative. This loss function enables GOWL to penalize the treatments corresponding to negative reward values properly to avoid the rewards shift problem previously described. We further study the proposed method both numerically and theoretically, and compare it with several alternative methods.

The remainder of the paper is organized as follows. In Section 2, we explain how the modified loss function for GOWL works under the binary treatment setting. In Section 3, we introduce GOWL for ITR estimation in the ordinal treatment setting. In Section 4, we establish the statistical learning properties of GOWL. Simulated data examples are used in Section 5, and an application to a type 2 diabetes mellitus observational study is provided in Section 6. We provide some discussions and conclusions in Section 7. Separate online supplementary materials include the computational algorithm, additional numerical results, and proofs of the theorems.

2 Generalized Outcome Weighted Learning for Binary Treatments

In this section, we give a brief review of OWL and its corresponding optimization problem. Motivated by the limitations of OWL, we propose a generalized version of OWL for the binary treatment case using a modified loss function.

2.1 Individual Treatment Rule and Outcome Weighted Learning

Suppose that we collect the data from a two-arm clinical study where the binary treatment is denoted by A ∈ 𝒜 = {−1, 1}. We assume that the patients’ covariates are represented by an n × p matrix X ∈ 𝒳, where 𝒳 denotes the covariate space, n is the number of patients enrolled, and p corresponds to the number of covariates. We also use a bounded random variable R to represent the clinical outcome reward and assume a larger R value is more desirable. Note that R can depend on both X and A. Under this framework, the ITR is a map 𝒟 : ℝ^p → 𝒜 which assigns a patient with X to the treatment 𝒟(X). There are key assumptions which build the connections between the observed outcome and the potential data (Rubin, 1978): positivity, strong ignorability, and consistency (details are given in the supplement). Under these three assumptions, Qian and Murphy (2011) showed that the goal of an optimal ITR is to find the map 𝒟 = 𝒟^* to maximize the marginal mean outcome reward under 𝒟^*, which can be equivalently expressed as,

$${\mathcal{D}}^{\ast }(\mathit{X})=\underset{\mathcal{D}}{argmin}\left\{E\left(\frac{R·I(A\ne \mathcal{D}(\mathit{X}))}{P(A\mid \mathit{X})}\mid \mathit{X}\right)\right\},$$ (1)

where P(A|X) is the prior probability of treatment A for X, and R·I(A ≠ 𝒟(X))/P(A|X) is a loss that can be understood as a measure of goodness of fit for 𝒟. Note that as a special case, a randomized clinical trial satisfies P(A|X) = P(A). Furthermore, the expectation in (1) is conditional on X for each given 𝒟. From now on, we omit the conditional part of the expectation to simplify the expressions. To estimate the optimal treatment rule 𝒟^*, one needs to obtain a classifier function f(x) such that 𝒟(x) = sign(f(x)). Thus, we have that I(A ≠ 𝒟(X)) = I(A · f(X) ≤ 0). To address the problem in (1), Zhao et al. (2012) proposed OWL by replacing the 0–1 loss above with the hinge loss used in the Support Vector Machine (SVM, Cortes and Vapnik (1995)) together with a regularization term to control model complexity. As a consequence, the regularized optimization problem becomes a search for the decision rule f which minimizes the objective function

$$\frac{1}{n}\sum _{i=1}^n\frac{r_i}{P(a_i\mid {\mathit{x}}_i)}{[1-a_{i}f({\mathit{x}}_i)]}_{+}+\lambda {\Vert f\Vert }^2,$$ (2)

where (x_i, a_i, r_i); i = 1,⋯, n, is a realization of (X,A,R) with a_i ∈ {−1, 1}, the function [u]₊ = max(u, 0) denotes the positive part of u, ||f||² is the squared L₂ norm of f and λ is the tuning parameter used to control the model complexity and avoid overfitting. To maintain the convexity of the objective function, OWL requires all rewards to be non-negative.

In practice, when there are negative rewards, one can shift them by a constant to ensure positiveness. Zhou et al. (2017) noted that such a constant shift process for the rewards may lead to suboptimal estimates. They noted that the optimal treatment estimates tend to be the same as the random treatments that are originally assigned. This situation can be further illustrated by a toy example as follows. Suppose we have two intervention groups (treatment and placebo) and two patients both being assigned to the treatment group and receiving rewards of −10 and 10, respectively. Such results imply that the first patient may not benefit from the treatment due to the corresponding negative feedback. If we follow the reward shift idea as mentioned above and add 15 to both rewards, then the model will probably draw an incorrect conclusion that both patients benefit from the treatment since both shifted rewards are positive. Another drawback of this rewards-shift strategy comes from the fact that there are an infinite number of constants one can choose for the shift. Different shift constants can lead to different coefficient estimates when the decision rule f has a certain parametric or nonparametric form in problem (2). An illustrating example about the reward shift issue is provided in the supplement. To solve this problem, we propose a generalized OWL in Section 2.2 which does not require rewards to be positive.

2.2 Generalized Outcome Weighted Learning

To better handle the data that has negative rewards, we consider reformulating the minimization problem (1) into two pieces as follows:

$$\underset{\mathcal{D}}{argmin}E\left\{\frac{\mid R\mid }{P(A\mid \mathit{X})}[I(R\ge 0)I(A\ne \mathcal{D}(\mathit{X}))+I(R<0)I(A=\mathcal{D}(\mathit{X}))]\right\}.$$ (3)

Note that (3) is equivalent to (1) because the term $\frac{R·I(R<0)}{P(A\mid \mathit{X})}$ is free of 𝒟(X). Similar to the discussion in Section 2.1, we can rewrite the optimization problem in (3) as follows, with 𝒟(X) = sign(f(X)):

$$\underset{\mathcal{D}}{argmin}E\left\{\frac{\mid R\mid }{P(A\mid \mathit{X})}[I(R\ge 0)I(A·f(\mathit{X})\le 0)+I(R<0)I(A·f(\mathit{X})>0)]\right\}.$$ (4)

Furthermore, to alleviate the computational intensity of solving (4), we use a modified loss function to be minimized with the population form expressed as

$$E\left\{\frac{\mid R\mid }{P(A\mid \mathit{X})}[I(R\ge 0){[1-Af(\mathit{X})]}_{+}+I(R<0){[1+Af(\mathit{X})]}_{+}]\right\}.$$ (5)

Here the ITR 𝒟 in (3) is the sign function of the decision rule f in (5) by definition. Therefore, the corresponding empirical sum on the training data with a L₂ norm penalty becomes

$$\sum _{i=1}^n\left\{\frac{\mid r_i\mid }{P(a_i\mid {\mathit{x}}_i)}[I(r_i\ge 0){[1-a_{i}f({\mathit{x}}_i)]}_{+}+I(r_i<0){[1+a_{i}f({\mathit{x}}_i)]}_{+}]\right\}+\lambda {\Vert f\Vert }^2.$$ (6)

Note that the loss in (6) has two parts by the sign of r_i. For observations with positive rewards, we use r_i as their weights for the corresponding loss function and penalize the misclassification by the standard hinge loss function l₁(u) = [1 −u]₊. This part is identical to the hinge loss in OWL. However, for the observations with negative rewards, we employ a modified hinge loss l₂ = [1+u]₊ which encourages the estimated decision function f(x_i) to move away from a_i when we have a large |r_i|, i.e. a small r_i. As a consequence, the modified loss function in (6) is piecewise convex in terms of a_if(x_i). Therefore, a global optimization solution of the objective function could be guaranteed when standard convex optimization algorithms are applied. One advantage of using the modified hinge loss is that the observed rewards are no longer required to be positive so that the problem caused by the non-unique reward shift can be circumvented. In addition, one can see that the loss function reduces to the standard hinge loss when all r_i > 0.

3 Generalized Outcome Weighted Learning for Ordinal Treatments

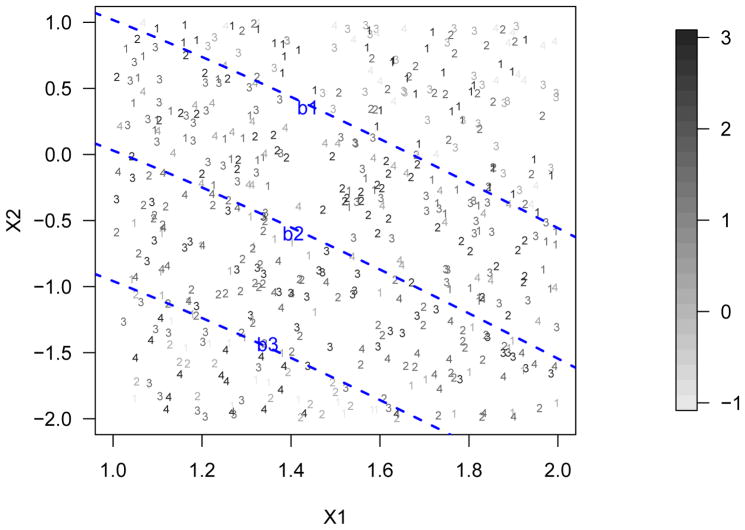
In this section, we discuss how to extend GOWL from binary treatments to ordinal treatments. To illustrate the ordinal treatment problems, Figure 1 shows a simulated example with two covariates and four treatment levels where the numbers represent the actually assigned treatments. The gray-scale of the numbers indicates the clinical outcome value and a darker color means a larger reward. The dashed lines indicate how the optimal ITR boundaries split the input space into four regions where the optimal treatment rule changes from 𝒟^* = 1 in the top right area to 4 in the bottom left one. For example, in the top right area where 𝒟^* = 1, it is clear that the rewards become less as the assigned treatment moves away from A = 1. For ordinal treatments, we assume that a treatment that is further away from the optimal one on one side receives a smaller reward than those treatments closer to the optimal one on the same side. Therefore, when compared with the general multicategory treatment, it is important to utilize this additional information of ordinal treatments when estimating ITRs. To this end, we borrow the data duplication idea in standard ordinal classification and develop our new procedure for GOWL with ordinal treatments.

Figure 1.

A simulation example explaining how the monotonic property works. In this case, there are two covariates and four treatment levels where the numbers represent the actually assigned treatments. The gray-scale of the numbers indicates the clinical outcome value and a darker color means a larger reward (see the gray-scale strip). The dashed lines indicate how the optimal ITR boundaries split the input space.

3.1 Classification of Ordinal Response with Data Duplication

For an ordinal response problem, suppose that each observation vector is ( ${\mathit{x}}_i^T$, y_i) where i = 1,⋯, n, the predictor x_i contains p covariates, and the response y_i ∈ {1,⋯,K}. Cardoso and Pinto da Costa (2007) proposed a data duplication technique to address this problem. To apply this idea, one first needs to generate a new dataset written as ( ${\mathit{x}}_i^{{(k)}^T},y_i^{(k)}$), where ${\mathit{x}}_i^{(k)}={({\mathit{x}}_i^T,{\mathit{e}}_k^T)}^T,y_i^{(k)}=\text{sign}(y_i-k),{\mathit{e}}_k^T$ is a K − 1 dimensional row vector whose kth element is 1 while others are zeros, and k = 1,⋯,K − 1. Thus, $y_i^{(k)}$ defines a new binary response indicating 1,⋯, k versus k+1,⋯,K. Here the sign(x) function is defined to be 1 when x > 0 and −1 otherwise. Then, the goal of the classification method is to find a surrogate binary classifier f(x^(k)) to $\text{minimize}{\sum }_{i=1}^n{\sum }_{k=1}^{K-1}l(y_i^{(k)},f({\mathit{x}}^{(k)}))+J(f)$, where l(·) is the pre-defined loss and J(f) is a penalty term. Once these $f({\mathit{x}}_i^{(k)})$ are obtained for k = 1,⋯,K − 1, then the predicted rule 𝒟̂(x_i) for the original ordinal outcome y_i can be calculated by $\widehat{\mathcal{D}}({\mathit{x}}_i)={\sum }_{k=1}^{K-1}I(f({\mathit{x}}_i^{(k)})>0)+1$, where I(·) is the indicator function.

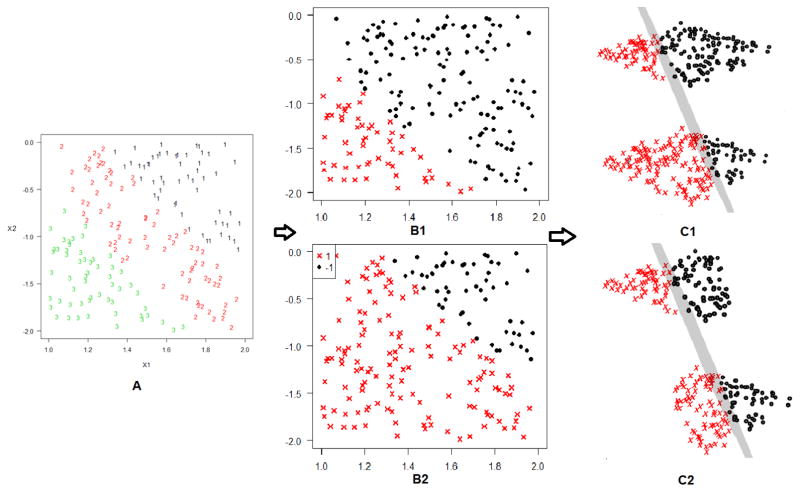
We use Figure 2 (Panel C1) to further illustrate this strategy using a toy example. Suppose there are two covariates, represented by the horizontal and vertical axes of the left plot, and three levels of the ordinal response, denoted by the numbers in the left panel. To build the targeted classifier, we first duplicate the original data once, and relabel the response as a binary variable in each of the duplicated datasets, shown in the middle panel. Then, we fit the entire duplicated dataset together using a binary classifier represented by the 3-dimensional gray plane in the right panel. Finally we map the binary classification results on each of the 2-dimensional duplicated datasets to obtain the final classifier for the ordinal problem. Note that the distance between these 2-dimensional duplicated datasets is treated as an additional parameter that needs to be estimated in this process.

Figure 2.

The idea of the two data duplicate strategies for a standard classification problem with an ordinal response. Panel A represents the original data with two covariates and three levels of the response, and Panels B1–B2 show how the duplicate strategies extend the feature space. Panels C1–C2 demonstrate how the first and second duplicated datasets can be used to build the targeted classifiers.

3.2 Generalized Outcome Weighted Learning

Now consider an extended version of clinical data (X,A,R) in Section 2 with X and R the same as before but with A being an ordinal treatment with A ∈ 𝒜 = {1,⋯,K}. We focus on the ordinal treatment scenario, in which the K categories of the treatment are ordered in the sense that treatments 1 and K are the most different treatements. For example, these treatments may represent different discrete dose levels with A = 1 being the lowest dose and A = K being the highest. Similar to Section 3.1, we define the duplicated random set (X^(k), A^(k),R^(k)) with its ith realization defined as ${\mathit{x}}_i^{(k)}={({\mathit{x}}_i^T,{\mathit{e}}_k^T)}^T,a_i^{(k)}=\text{sign}(a_i-k)$, and $r_i^{(k)}=r_i$ for k = 1,⋯,K − 1. According to the value function definition from Qian and Murphy (2011), we let P^𝒟_k denote the conditional distribution of (X,A,R) on A^(k) = 𝒟(X^(k)). Then, with the duplicated data set and a map 𝒟 from each X^(k) to {−1, 1} for k = 1,⋯,K−1, we propose a new conditional expected reward to be maximized as follows:

$$\begin{gathered} \sum _{k=1}^{K-1}E\left(R^{(k)}\mid A^{(k)}=\mathcal{D}({\mathit{X}}^{(k)}),\mathit{X}\right)=\sum _{k=1}^{K-1}\int R^{(k)}\frac{d{P}^{{\mathcal{D}}_k}}{dP}dP \\ =\sum _{k=1}^{K-1}E\left(\frac{R^{(k)}·I(A^{(k)}=\mathcal{D}({\mathit{X}}^{(k)}))}{P(A\mid \mathit{X})}\right). \end{gathered}$$ (7)

Similar to Qian and Murphy (2011) and Zhao et al. (2012), we refer to (7) as the value function of 𝒟 and denote it by 𝒱(𝒟). In this way, the optimal map 𝒟^* is defined as

$${\mathcal{D}}^{\ast }=\underset{\mathcal{D}}{argmin}\sum _{k=1}^{K-1}E\left(\frac{R^{(k)}·I(A^{(k)}\ne \mathcal{D}({\mathit{X}}^{(k)})}{P(A\mid \mathit{X})}\right),$$ (8)

where the denominator serves as the weight for each subject according to the actual assigned treatment. Once the map 𝒟 is estimated, one can obtain the corresponding ITR estimate of X by using $\widehat{\mathcal{D}}(\mathit{X})={\sum }_{k=1}^{K-1}I(f({\mathit{X}}^{(k)})>0)+1$.

Optimal treatment estimation through (8) can be effective when the treatment is ordinal due to the way it utilizes the ordinality information. In particular, the new minimization problem considers the distance between the estimated optimal treatment and the actually assigned treatment by counting the number of categories k for which D(X^(k)) does not match A^(k) for k = 1,⋯,K −1. In this way, the proposed method attempts to penalize the near misses less than the awful decisions because a near miss corresponds to a smaller number of mismatches. In the extreme case when a certain subject has a very large positive reward value, the estimated 𝒟(X^(k)) would be likely to match A^(k) for all k = 1,⋯,K − 1, which results in 𝒟̂(X) = A. In contrast, it may imply that the actually assigned treatment is suboptimal when the reward takes a small value. Some of the estimated 𝒟(X^(k)) will not match the observed A^(k) as the estimated rule approximates the global minimizer of (8).

To address the problem (8), we replace the 0–1 loss with the modified loss in (6) and add the model complexity penalty term to avoid overfitting. Thus, the new objective function on ( ${\mathit{x}}_i^{(k)},a_i^{(k)},r_i^{(k)}$) becomes

$$\sum _{i=1}^n\sum _{k=1}^{K-1}\frac{\left|r_i^{(k)}\right|}{P(a_i\mid {\mathit{x}}_i)}\left[I(r_i^{(k)}\ge 0){\left[1-a_i^{(k)}f({\mathit{x}}_i^{(k)})\right]}_{+}+I(r_i^{(k)}<0){\left[1+a_i^{(k)}f({\mathit{x}}_i^{(k)})\right]}_{+}\right]+\lambda {\Vert f\Vert }^2,$$ (9)

where ${\mathit{x}}_i^{(k)}$ is the kth duplication of the ith original subject and $f({\mathit{x}}_i^{(k)})$ is the corresponding binary classifier. Similarly, the predicted optimal ITR of the ith subject x_i can be obtained by $\widehat{\mathcal{D}}({\mathit{x}}_i)={\sum }_{k=1}^{K-1}I(f({\mathit{x}}_i^{(k)})>0)+1$.

In Section 4, we show that the method with the data duplicate strategy proposed above enjoys Fisher consistency, in the sense that the estimate matches $\underset{\mathcal{D}}{argmax}E(R\mid \mathit{X},\mathcal{D})$ asymptotically under an assumption on rewards. To alleviate this reward assumption, we propose a second data duplicate strategy. Specifically, we redefine the duplicated reward as $r_i^{(k)}=r_i$ only when a_i ∈ {k, k+1}, while keeping all the other duplicated variables the same as before. This modified strategy uses partial data in each binary treatment subproblem so that only ordinality of treatments is required for Fisher consistency. Panels C1 and C2 of Figure 2 compare the two duplicate strategies using the same example at the end of Section 3.1. The second strategy uses subsets of data and may work well for large samples. In particular, it is well suited for the cases where there are sufficient data within each treatment group.

To solve the optimization problem in (9), we develop an algorithm based on the primal-dual formula for the SVM (Vazirani, 2013). In particular, due to the convexity of the objective function, we reformulate (9) into a minimization problem with linear constraints, and then derive the corresponding Lagrange function for the primal and dual problems. We use the Python package CVXOPT to solve the dual problem that includes both linear and nonlinear decision functions. For the nonlinear case, we apply the kernel learning approach in Reproducing Kernel Hilbert Spaces (RKHS, Kimeldorf and Wahba (1970)). Briefly, the classification function classifier f(x_j) for the Gaussian kernel can be written as ${\sum }_{i=1}^{n}k({\mathit{x}}_i,{\mathit{x}}_j){\alpha }_i+b$, where the kernel function $k({\mathit{x}}_i,{\mathit{x}}_j)=exp(-{\Vert {\mathit{x}}_i-{\mathit{x}}_j\Vert }^2/2{\sigma }_n^2)$ and σ_n is the bandwidth. The details of the algorithm are provided in the supplement.

The decision function can always be expressed in the form f(x^(k)) = g(x) + b_k for k = 1,⋯,K − 1, under both linear and kernel learning spaces. We take the linear space as an example and a similar discussion for the kernel space is left in the supplement. For a linear f, we can express $f({\mathit{x}}_i^{(k)})={[{\mathit{x}}_i^{(k)}]}^T\stackrel{\sim }{\beta }+\stackrel{\sim }{b}={\mathit{x}}_i\beta +b_k$ due to the definition ${\mathit{x}}_i^{(k)}={({\mathit{x}}_i^T,{\mathit{e}}_k^T)}^T$, where ${\mathit{e}}_k^T$ is a K − 1 dimensional row vector whose kth element is one while the others are zeros. Note that the ordinality of treatments is sufficient to ensure that the estimated f(X^(k)) is monotonically ordered by k. The monotonic property ensures that the estimated ITR matches the order of treatments. In Section 4, we show that the intercepts b_k for k = 1,⋯,K − 1 can have such a monotonic property.

4 Statistical Learning Theory

In this section, we show Fisher consistency of the estimated ITR, and the monotonic property of the intercepts. We also study the consistency and convergence rate of the risk bound for the estimated ITR using GOWL but leave these details to the supplement.

4.1 Fisher Consistency

We define the ϕ–risk associated with the surrogate loss in (5) as ${\mathcal{R}}_{\varphi }(f)={\sum }_{k=1}^{K-1}{\mathcal{R}}_{\varphi }^{(k)}(f)$ where ${\mathcal{R}}_{\varphi }^{(k)}(f)=E[\frac{\mid R^{(k)}\mid }{P(A\mid \mathit{X})}\varphi (A^{(k)}f({\mathit{X}}^{(k)}),R^{(k)})]$ and ϕ(u, r) = I(r ≥ 0)[1 − u]₊ + I(r < 0)[1 + u]₊. We also define the minimizer of ℛ_ϕ(f) as $f_{\varphi }^{\ast }$ with its corresponding surrogate optimal ITR expressed as ${\mathcal{D}}_{\varphi }^{\ast }(\mathit{X})={\sum }_{k=1}^{K-1}I(f_{\varphi }^{\ast }({\mathit{X}}^{(k)})>0)+1$. Recall that the targeted optimal ITR 𝒟^* always corresponds to the treatment that can produce the best expected clinical reward, i.e. ${\mathcal{D}}^{\ast }(\mathit{X})=\underset{k\in \mathcal{A}}{argmax}[E(R\mid \mathit{X},A=k)]$. To derive Fisher consistency, we need to show that by using the surrogate loss ϕ to replace the 0–1 loss, the surrogate optimal ITR ${\mathcal{D}}_{\varphi }^{\ast }(\mathit{X})$ matches 𝒟^*(X). We divide the process into two steps: first, we show in Lemma 4.1 that ${\mathcal{D}}_{\varphi }^{\ast }(\mathit{X})={\mathcal{D}}^{\ast }(\mathit{X})$ for binary treatments. Second, the result can be generalized to ordinal treatments with an additional assumption in Theorem 4.2.

Lemma 4.1

When A ∈ {1, 2}, for any measurable function f, we have ${\mathcal{D}}_{\varphi }^{\ast }(\mathit{X})=I(f_{\varphi }^{\ast }({\mathit{X}}^{(1)})>0)+1={\mathcal{D}}^{\ast }(\mathit{X})$.

Theorem 4.2

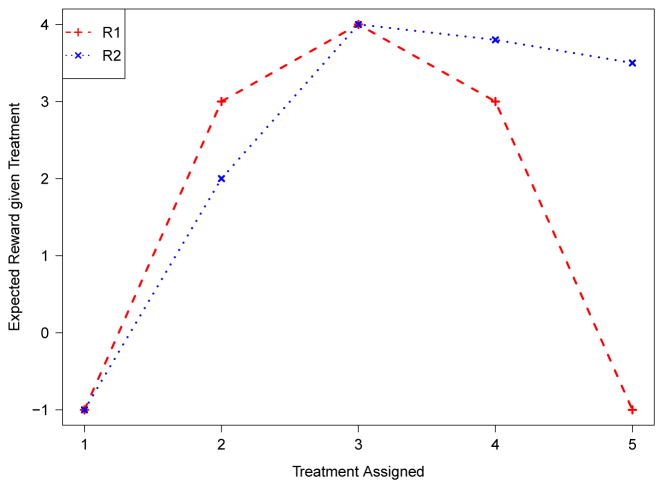
For the first data duplicate strategy with A ∈ {1,⋯,K} and K >2, when E(R|X, A > k) > E(R|X, A ≤ k) if 𝒟^*(X) > k, and E(R|X, A ≤ k) > E(R|X, A > k) if 𝒟^*(X) ≤ k for k = 1,⋯,K − 1, then ${\mathcal{D}}_{\varphi }^{\ast }(\mathit{X})={\sum }_{k=1}^{K-1}I(f_{\varphi }^{\ast }({\mathit{X}}^{(k)})>0)+1={\mathcal{D}}^{\ast }(\mathit{X})$. The assumption on E(R|X) in Theorem 4.2 is used to accumulate all $f_{\varphi }^{\ast }({\mathit{X}}^{(k)})$ correctly to reach 𝒟^*(X). Thus, this assumption requires that the reward curve decreases at a similar rate when the treatment is away from the optimal one at both sides of its peak (see the R1 curve in Figure 3). It is only a sufficient condition for Fisher consistency, and it ensures each binary surrogate classifier $I(f_{\varphi }^{\ast }({\mathit{X}}^{(k)})>0)$ to match the corresponding optimal binary classifier I(f^*(X^(k)) > 0) in each binary subproblem. As discussed in the previous section, such an assumption is no longer needed if the second data duplicate strategy is used.

Figure 3.

Examples when the assumption holds and fails for Theorem 4.2. In this case, 𝒟^*(x_i) = 3 and the assumption in Theorem 4.2 holds for curve R1 but fails for curve R2. The assumption of the modified duplication strategy that $r_i^{(k)}=r_i$ if a_i ∈ {k, k + 1} holds for both curves.

4.2 Monotonic Boundary

In Section 3, we discussed that the decision function f(X^(k)) can be expressed as g(X)+b_k for both linear and nonlinear cases. The following theorem shows that the intercepts b_k for k = 1,⋯,K − 1 can have the monotonic property under certain assumptions so that the resulting rule has no contradiction.

Theorem 4.3

If we write the decision function as f(X^(k)) = g(X) + b_k; k = 1,⋯,K − 1, and assume that the signs of E [R|A = k] are the same for k = 2,⋯,K− 1, then the optimal solution (g, b) for minimizing the ϕ-risk ℛ_ϕ(f) has monotonic b values. In particular, we have b_k > b_k+1 (b_k < b_k+1) for k = 1,⋯,K−2 when E [R|A = k] > 0 (< 0) for k = 2,⋯,K−1.

To understand the condition in Theorem 4.3, note that the value of E[R|A = k] is the average benefit patients receive from taking the treatment k. Violating the conditions in Theorem 4.3 may destroy the monotonic order of b. For example, when E [R|A = m] for certain m ∈ {2,⋯,K − 1} is observed to be negative while all the other E[R|A = k] are positive, no patient would be assigned the treatment m as the optimal treatment and the corresponding b would not be monotonic.

We use Figure 1 to further illustrate the condition in Theorem 4.3. Starting with all positive E[R|A = k], if we decrease E[R|A = 2] while keeping the other E[R|A = k] values constant, the margin between b₁ and b₂ will be narrower. Such a change indicates that a smaller proportion of the population will be assigned A = 2 as the optimal treatment. In the extreme case where E[R|A = 2] is negative and small enough compared to the other two treatments, the boundaries of b₁ and b₂ will overlap, violating the monotonic property. Under this circumstance, the rewards can contradict the ordinality of the treatments.

Finally, we would like to emphasize that Theorem 4.3 only presents a sufficient condition for the monotonicity of the intercepts. Moreover, the signs of E[R|A = 1] and E[R|A = K] do not impact the monotonicity of the boundaries because they are on the edges.

5 Simulation Study

We conduct simulation studies with both linear and nonlinear ITR boundaries to assess the performance of GOWL. In both cases, we first generate a training set with the covariates X₁,⋯,X_p from a uniform distribution U (−1, 1) and treatment A from a discrete uniform distribution from 1 to K. The reward follows N(Q(X, A), 1) with Q(X, A) = μ(X) + t(X, A), where the t(X, A) is the interaction that determines the true optimal treatment. We also generate an independent equal-size tuning set and a much larger testing set (10 times as large as the training set) with the same variables in each scenario. The tuning set is used to select the optimal tuning parameter λ and the Gaussian kernel bandwidth σ_n. In particular, we choose λ from { $\frac{i}{n}$; i = 0.1, 1, 10, 100, 500} and σ_n from {0.1, 1, 10}, where n is the tuning size. The testing set is used to check the prediction performance of the models.

For comparisons, we adapt some existing methods to ordinal treatment cases. Specifically, we pick two methods: OWL conducted by a series of pairwise comparisons between {1,⋯, k} and {k + 1,⋯,K} for k = 1,⋯,K − 1, and l₁ penalized least squares (PLS-l₁) that relabels the treatment as K − 1 binary variables and includes two way covariate-treatment interactions. The estimated optimal treatment for OWL is obtained by summing through all pairwise prediction results. For OWL, the original reward is shifted to be all positive. For OWL and GOWL, both the linear kernel (OWL-Linear and GOWL-Linear) and the Gaussian kernel (OWL-Gaussian and GOWL-Gaussian) are used. Two criteria are used to evaluate the model performance: the misclassification rate (MISC), and the mean of squares of the difference between the estimated value functions versus the optimal value functions (VMSE). Smaller values are preferred for both criteria by definition. The first criterion measures the proportion of correct treatment assignments. The second criterion is a more comprehensive measure on how close the estimated ITR is to the optimal ITR. The value function estimate is defined as ${\mathbb{P}}_n^{\ast }[{\sum }_{k=1}^{K-1}I(A^{(k)}=\mathcal{D}({\mathit{X}}^{(k)}))R/P(A)]/{\mathbb{P}}_n^{\ast }[{\sum }_{k=1}^{K-1}I(A^{(k)}=\mathcal{D}({\mathit{X}}^{(k)}))/P(A)]$, where ${\mathbb{P}}_n^{\ast }$ denotes the empirical average of the testing dataset.

5.1 Linear Boundary Examples

We consider the following four scenarios with μ(X) and t(X, A) defined as,

1. Example 1 (K = 2): μ(X) = 1+X₁ + X₂ + 2X₃ + 0.5X₄, t(X, A) = 1.8(0.3 − X₁ − X₂)(2A − 3), and P(A = 2|X) = exp(X₁)/(exp(X₁) + 1);

2. Example 2 (K = 3): μ(X) = −5 + 2X₁ + X₂ + 0.5X₃, $t(\mathit{X},A)=4{\sum }_{i=1}^{3}I(g(\mathit{X})\in (-b_{i-1},-b_i])(2-\mid A-i\mid )$, g(X) = X₁−2X₂−X₃−0.6X₄+1.5(X₅−X₆), P(A = k|X) = k/6, b₀ = ∞, b₁ = 0.5, b₂ = −1, b₃ = −∞;

3. Example 3 (K = 5): μ(X) = 2X₁+X₂+0.5X₃, $t(\mathit{X},A)=4{\sum }_{i=1}^{5}I(g(\mathit{X})\in (-b_{i-1},-b_i])(2-\mid A-i\mid )$, where g(X) = X₁ −2X₂ −X₃ −0.6X₄ +1.5(X₅ −X₆), P(A|X) = 1/5, b₀ = ∞, b₁ = 1.9, b₂ = 0.5, b₃ = −0.5, b₄ = −1.7 and b₅ = −∞;

4. Example 4 (K = 7): μ(X) = 2 + 2X₁ + X₂ + 0.5X₃, $t(\mathit{X},A)=4{\sum }_{i=1}^{7}I(g(\mathit{X})\in (-b_{i-1},-b_i])(2-\mid A-i\mid )$, where g(X) = X₁ −2X₂ −X₃ −0.6X₄ +1.5(X₅ −X₆), P(A = k|X) = 0.1+0.1I(k ≥ 5), (b₀, b₁, b₂, b₃, b₄, b₅, b₆, b₇) = (∞, 2.1, 1.2, 0.4, −0.4, −1, −2.1, −∞).

In these simulatations, the true boundaries are parallel to each other. The cut-off values b are set to encourage an evenly distributed true optimal treatment from 1 to K. Furthermore, the t(X, A)’s are set to ensure that the reward outcome decreases symmetrically when the assigned treatment moves away from the optimal treatment towards high or low levels. To investigate the model performance when some crucial assumptions do not hold, we consider examples violating the assumptions of Fisher consistency in Theorem 4.2 and the sufficient condition of the monotonicity property in Theorem 4.3. In particular, the sufficient condition of monotonicity does not hold in Example 4, and Examples 3 and 4 are the scenarios when Fisher consistency cannot be guaranteed. Examples 1, 2 and 4 are for situations where the treatment assignment is not completely at random. The propensity score is estimated by logistic regression in Example 1, and approximated by sample treatment frequencies in the other examples. The training sample sizes are listed in Table 1, which range from 300 to 500. We repeat the simulation 500 times and present the testing prediction results in Table 1.

Table 1.

Results of linear boundary examples: K represents the number of treatment levels; n represents the training set size; the MISC rows show the means and standard deviations (in parenthesis) of the misclassification rates; and the VMSE rows show the means and standard deviations (in parenthesis) of the value function MSEs. PLS-l₁ represents penalized least squares including covariate-treatment interactions with l₁ penalty (Qian and Murphy, 2011); OWL represents the outcome weighted learning, and GOWL1 and GOWL2 represent the proposed generalized outcome weighted learning with the first and second data duplication methods. In each scenario, the model producing the best criterion is in bold.

Methods	(K, n)	(2,300)		(3,300)	(5,500)	(7,500)
PLS-l1	MISC	0.138 (0.010)		0.271 (0.076)	0.443 (0.009)	0.688 (0.153)
	VMSE	0.060 (0.016)		0.134 (0.032)	0.365 (0.016)	0.497 (0.281)
OWL-Lin	MISC	0.089 (0.025)		0.262 (0.116)	0.308 (0.031)	0.392 (0.200)
	VMSE	0.149 (0.065)		0.327 (0.186)	0.412 (0.133)	0.304 (0.261)
OWL-Gau	MISC	0.139 (0.035)		0.251 (0.070)	0.371 (0.062)	0.592 (0.159)
	VMSE	0.049 (0.035)		0.318 (0.153)	0.419 (0.340)	0.371 (0.160)
GOWL1-Lin	MISC	0.070 (0.036)		0.064 (0.029)	0.136 (0.038)	0.226 (0.072)
	VMSE	0.014 (0.025)		0.059 (0.066)	0.022 (0.009)	0.063 (0.007)
GOWL1-Gau	MISC	0.064	(0.035)	0.096 (0.037)	0.154 (0.019)	0.325 (0.061)
	VMSE	0.008	(0.014)	0.106 (0.057)	0.020 (0.007)	0.051 (0.004)
GOWL2-Lin	MISC	0.070 (0.036)		0.087 (0.043)	0.146 (0.060)	0.247 (0.068)
	VMSE	0.014 (0.025)		0.045 (0.030)	0.028 (0.024)	0.038 (0.040)
GOWL2-Gau	MISC	0.064	(0.035)	0.123 (0.041)	0.186 (0.084)	0.348 (0.057)
	VMSE	0.008	(0.014)	0.102 (0.117)	0.093 (0.104)	0.167 (0.174)

As shown in Table 1, the proposed GOWL under both data duplication methods delivers competitive accuracy rates in predicting ITR for testing datasets in most of the cases. The results of these two methods are the same for the first example because they are equivalent when K = 2. In general, when the number of treatment classes K is small, a linear model such as PLS-l₁ can be competitive because the true decision boundary is linear. However, when K increases to 5 or 7, GOWL outperforms all the other methods, especially in terms of the value function of the estimated ITR. Moreover, for the binary treatment, GOWL performs comparably to OWL whereas PLS-l₁ shows relatively worse results with a larger misclassification and a worse value function. When the number of treatment category K increases, the advantage of GOWL becomes more significant in terms of both the misclassification rate and value function comparisons. Furthermore, under the true linear boundary cases, the performance of GOWL with the Gaussian kernel can be comparable to the case with the linear kernel when a proper tuning parameter is used. Thus a flexible nonparametric estimation procedure can be considered in practice when there is no prior knowledge about the shape of the underlying ITR boundaries.

Comparing the first and second data duplication strategies, one can conclude that the method guaranteeing Fisher consistency under the ordinal treatment does not necessarily always have better estimated ITR results. This may be due to the fact that Fisher consistency can only be achieved under infinity samples and a decision function space that covers the optimal one. Therefore, we recommend both strategies to be considered and compared in practice to optimize the ITR estimation performance. In addition, we still obtain a monotonic estimated ITR boundaries for Examples 4, although the sufficient condition stated in Theorem 4.3 does not hold. Thus, violation of such a condition does not necessarily generate controversial estimated ITR results.

5.2 Nonlinear Boundary Examples and Other Comparisons

We assess the performance of GOWL using nonlinear boundary examples and compare it with other methods. The results are provided in Table 2. In all four examples, PLS-l₁ performs the worst due to its incorrect model specification. Similar to the linear boundary examples, GOWL-Gaussian with both data duplicate strategies outperform OWL-Gaussian in terms of both classification accuracy and value functions. The results of the two data duplicate methods are still similar. Finally, we find that none of the methods performs well when the true boundaries have complex structures as the case for K = 7. Detailed additional simulation settings and results are provided in the supplementary materials.

Table 2.

Results of nonlinear boundary examples: K represents the number of treatment levels; n represents the training set size; the MISC rows show the means and standard deviations (in parenthesis) of the misclassification rates; and the VMSE rows show the means and standard deviations (in parenthesis) of the value function MSEs. PLS-l₁ represents penalized least squares including covariate-treatment interactions with l₁ penalty (Qian and Murphy, 2011); OWL represents the outcome weighted learning, and GOWL1 and GOWL2 represent the proposed generalized outcome weighted learning with the first and second data duplication methods. In each scenario, the model producing the best criterion is in bold.

Methods	(K, n)	(2,300)	(3,300)	(5,500)	(7,500)
PLS-l1	MISC	0.399 (0.110)	0.493 (0.189)	0.552 (0.099)	0.746 (0.377)
	VMSE	1.327 (0.427)	1.275 (0.564)	1.601 (0.325)	1.502 (0.894)
OWL-Lin	MISC	0.204 (0.016)	0.381 (0.055)	0.460 (0.089)	0.686 (0.224)
	VMSE	0.489 (0.060)	0.912 (0.429)	1.780 (0.448)	1.659 (0.532)
OWL-Gau	MISC	0.177 (0.027)	0.351 (0.155)	0.373 (0.249)	0.683 (0.222)
	VMSE	0.097 (0.064)	0.712 (0.429)	1.311 (0.471)	1.694 (0.557)
GOWL1-Lin	MISC	0.217 (0.009)	0.362 (0.042)	0.387 (0.022)	0.641 (0.168)
	VMSE	0.222 (0.049)	0.453 (0.130)	0.681 (0.146)	1.085 (0.371)
GOWL1-Gau	MISC	0.092 (0.034)	0.152 (0.047)	0.251 (0.081)	0.529 (0.124)
	VMSE	0.023 (0.012)	0.112 (0.064)	0.189 (0.042)	0.622 (0.112)
GOWL2-Lin	MISC	0.217 (0.009)	0.386 (0.038)	0.392 (0.018)	0.660 (0.214)
	VMSE	0.222 (0.049)	0.462 (0.276)	0.634 (0.127)	1.280 (0.279)
GOWL2-Gau	MISC	0.092 (0.034)	0.144 (0.036)	0.264 (0.125)	0.514 (0.135)
	VMSE	0.023 (0.012)	0.177 (0.068)	0.231 (0.077)	0.448 (0.154)

Our focus has been on examples with parallel boundaries. The proposed GOWL can also work well when the parallel assumption of the true boundaries does not hold. Under these circumstances, one can consider using nonlinear learning so that the estimated boundaries would be flexible enough to approach the underlying true boundaries. An illustrating example is provided in the online supplementary material. In addition, some comparisons with the continuous dose method by Chen et al. (2016) are included in the supplementary material as well. The comparison shows that GOWL can provide competitive ITR estimation results under the scenario that a continuous dose is categorized into multiple ordinal treatments.

6 Application to a Type 2 Diabetes Study

We apply GOWL to a type 2 diabetes mellitus clinical observational (T2DM) study to assess its performance in real studies. We include people with T2DM during 2012–2013, from the clinical practice research datalink (CPRD (2015); see Herrett et al. (2015)). Three anti-diabetic therapies have been considered in this study: glucagon-like peptide-1 (GLP-1) receptor agonist, a regime including short-acting insulin, and long-acting insulin only. Some recent research showed that GLP-1 receptor agonists can be a good alternative for rapid-acting insulin (Ostroff, 2016). In this way, the three treatments can be ranked by the acting speed as well as the length of period that their effects last, and hence can be considered as three levels of an ordinal treatment. The primary target variable is the change of HbA1c before and after the treatment. Seven clinical factors are used including age, gender, ethnicity, body mass index, high-density lipoprotein cholesterol (HDL), low-density lipoprotein cholesterol (LDL), and smoking status. Several disease history variables are also included, such as angina, congestive heart failure, myocardial infraction, and stroke.

We provide some details on the data preprocessing including missing data in the supplement. The way that we handle the missing observations has limitations, and may possibly lead to biased conclusions. Alternatively, one can use various data imputation techniques to handle the missing data. After the data preprocessing, there are 10 covariates with 142 observations in total. We apply PLS-l₁, OWL-Linear, OWL-Gaussian, GOWL-Linear, and GOWL-Gaussian with both data duplicate strategies to estimate the ITR with the first three methods modified in the same way. We use the inverse value of the HbA1c change as the reward in estimating the ITR since a smaller HbA1c is desired. In order to obtain the propensity score P(A|X) before using OWL and GOWL, we fit an ordinal logistic model using the treatment as the response and all 10 covariates as predictors. As to the criterion, we calculate the predicted value function using the same formula as in the simulation study over 500 replications of 5-fold cross-validation. Table 3 summarizes the means and standard deviations of the empirical value functions from the training and validation sets.

Table 3.

Analysis Results for the T2DM Dataset. Empirical Value Function Results using 5-fold Cross-Validation are reported. For comparison, the original assigned treatment strategy has the value function 2.205 and the randomly assigned treatment method has average value function 2.104 in testing sets with standard deviation 0.131.

Model	Training	Testing
PLS-l1	2.242 (0.001)	2.173 (0.058)
OWL-Linear	2.371 (0.012)	2.316 (0.069)
OWL-Gaussian	2.451 (0.011)	2.285 (0.049)
GOWL1-Linear	2.374 (0.039)	2.341 (0.088)
GOWL2-Linear	2.382 (0.036)	2.325 (0.093)
GOWL1-Gaussian	2.488 (0.021)	2.387 (0.062)
GOWL2-Gaussian	2.452 (0.020)	2.367 (0.075)

To further demonstrate how much improvement the proposed method can obtain, we also calculate the value function with the original treatments and the average value function with treatment being randomly assigned 50 times. The empirical means of the value functions are 2.205 and 2.104 with the standard deviation for the random assignment being 0.131.

According to Table 3, GOWL achieves both the highest mean and the lowest standard deviation of the empirical value function in the prediction results. In addition, the three linear models are outperformed by the nonlinear models, possibly due to their suboptimal model specification for this application. As to the distribution of estimated optimal treatment assignments, the PLS-l₁ only includes long-acting insulin as the optimal treatment. OWL-Gaussian chooses approximately 83% of the patients to be in either the GLP-1 group or short-acting insulin group. GOWL1-Gaussian assigns approximately 50% patients into the short-acting insulin group while assigning the rest into one of the other two groups in a more even way. This conclusion is consistent with some literature on short-acting insulins, which shows the benefit of reducing HbA1c (Holman et al., 2007). Moreover, it is worth noting that prandial insulins also have elevated risk of hypo and weight gain, which are crucial safety and efficacy measurements for diabetes patients. Our study only considers HbA1c change as the outcome. One can consider more composite metrics, including HbA1c change, hypo events, and weight gain, to find the corresponding optimal treatment rules.

To investigate the interpretability of estimated ITRs, we compare the coefficients of PLS-l₁ with those of GOWL1 using the linear kernel. The main results are reflected on the covariates of gender, age, baseline high-density and low-density lipoprotein cholesterol (HDL and LDL), and some of the disease history indicators. In particular, PLS-l₁ suggests a longer acting therapy for females and elders, and the patients who did not have congestive heart failure and myocardial infraction history. In addition, PLS–l₁ indicates that patients with higher baseline lipoprotein cholesterol, both HDL and LDL, can be better treated by longer acting therapies. In contrast, GOWL1 suggests that male patients with lower baseline LDL and certain heart disease records may take longer acting therapies. Both methods agree that patients with higher baseline HbA1c should take longer acting therapies.

7 Conclusion

In this paper, we use a modified loss function to improve the performance of OWL and then generalize OWL to solve the ordinal treatment problems. In particular, the proposed GOWL converts the optimal ordinal treatment finding problem into multiple optimal binary treatment finding subproblems under certain restrictions. The estimating process produces a group of estimated optimal treatment boundaries with monotonic intercepts that never cross. Such boundaries can make the ITR estimates more stable and interpretable in practice.

There are various possible extensions for GOWL that could be considered. For example, one can incorporate a variable selection component into the objective function. In the literature, Xu et al. (2015) proposed variable selection in the linear case and Zhou et al. (2017) extended the idea for kernel learning. According to their ideas, one natural extension for GOWL is to include an l₁ penalty of the parameters in its optimization problem. In this way, variable sparsity could be achieved simultaneously when detecting the optimal ITR. The second possible extension that may improve the performance of GOWL is to modify the outcome in its optimization problem which is originally the reward R. Specifically, according to Fu et al. (2016), one can consider fitting a model with R versus X and then put the residuals as the outcome in the optimization problem of GOWL instead. Such an adjustment is likely to further improve the ITR estimation results for some finite sample scenarios.