Predictability, force, and (anti)resonance in complex object control

Abstract

Manipulation of complex objects as in tool use is ubiquitous and has given humans an evolutionary advantage. This study examined the strategies humans choose when manipulating an object with underactuated internal dynamics, such as a cup of coffee. The dynamics of the object renders the temporal evolution complex, possibly even chaotic, and difficult to predict. A cart-and-pendulum model, loosely mimicking coffee sloshing in a cup, was implemented in a virtual environment with a haptic interface. Participants rhythmically manipulated the virtual cup containing a rolling ball; they could choose the oscillation frequency, whereas the amplitude was prescribed. Three hypotheses were tested: 1) humans decrease interaction forces between hand and object; 2) humans increase the predictability of the object dynamics; and 3) humans exploit the resonances of the coupled object-hand system. Analysis revealed that humans chose either a high-frequency strategy with antiphase cup-and-ball movements or a low-frequency strategy with in-phase cup-and-ball movements. Counter to hypothesis 1, they did not decrease interaction force; instead, they increased the predictability of the interaction dynamics, quantified by mutual information, supporting hypothesis 2. To address hypothesis 3, frequency analysis of the coupled hand-object system revealed two resonance frequencies separated by an antiresonance frequency. The low-frequency strategy exploited one resonance, whereas the high-frequency strategy afforded more choice, consistent with the frequency response of the coupled system; both strategies avoided the antiresonance. Hence, humans did not prioritize small interaction forces but rather strategies that rendered interactions predictable. These findings highlight that physical interactions with complex objects pose control challenges not present in unconstrained movements.

NEW & NOTEWORTHY Daily actions involve manipulation of complex nonrigid objects, which present a challenge since humans have no direct control of the whole object. We used a virtual-reality experiment and simulations of a cart-and-pendulum system coupled to hand movements with impedance to analyze the manipulation of this underactuated object. We showed that participants developed strategies that increased the predictability of the object behavior by exploiting the resonance structure of the object but did not minimize the hand-object interaction force.

INTRODUCTION

The use of tools has been essential in human evolution, and a large variety of tools now enhance and augment our daily actions. Tool-supported actions range from the simple swinging of a hammer and cutting meat with a knife to more complex or exotic actions, such as eating spaghetti and cracking a whip. The latter tasks are challenging and require practice because the objects themselves, spaghetti and whip, are flexible, hence underactuated, i.e., have internal degrees of freedom that are not directly controlled by the user. Another seemingly mundane example is carrying a cup of coffee: the human manipulates the cup that, in turn, exerts a force on the coffee that exerts forces back on the cup and the hand. Complex interaction forces arise among the hand, the cup, and the coffee. Despite this complexity, humans are extremely skilled at interacting with such underactuated objects. Our understanding of how humans achieve such dexterity is still limited and becomes an ever-growing barrier to current developments in prosthesis control, brain-machine interfaces, and robotic rehabilitation.

Despite the abundant literature on the control of goal-directed upper-limb movements, most studies have focused on free movements without physical interaction, such as reaching and pointing (Bhushan and Shadmehr 1999; Flash and Hogan 1985; Krakauer et al. 1999; Sabes 2000), or interactions with rigid objects, such as grasping with isometric grip forces (Flanagan and Wing 1997; Fu and Santello 2014). The control of “complex objects,” which we define as objects with underactuated internal dynamics, i.e., nonrigid objects, has been largely ignored. The few studies that examined the control of complex objects have focused on the two classic control models of balancing a pole and manipulating a linear mass-spring system. For balancing a pole, one needs to stabilize an inherently unstable inverted pendulum. Based on kinematic measurements and mathematical modeling, different mechanisms have been suggested, such as intermittent, continuous, or predictive control, with forward or inverse models (Gawthrop et al. 2013; Insperger et al. 2013; Mehta and Schaal 2002). Another set of studies on the inverted pendulum system focused on noise and delays to distinguish between the continuous vs. intermittent nature of control (Cluff et al. 2009; Milton 2011; Milton et al. 2013). A linear mass-spring system has served as a model to examine optimization criteria in human control, such as generalized kinematic smoothness (Dingwell et al. 2004), effort and accuracy (Nagengast et al. 2009), and minimum acceleration with constraints on the center of mass (Leib and Karniel 2012). Two studies compared the contributions of visual and haptic feedback, and their results highlighted the essential role of haptic feedback over visual feedback in controlling the object (Danion et al. 2012; Huang et al. 2007). Finally, another set of studies looked at the compression of a buckling spring, modeling the buckling behavior with a subcritical pitchfork bifurcation of the nonlinear dynamic system, including integration of multisensory information with different time delays (Mosier et al. 2011; Venkadesan et al. 2007).

All of these studies examined point-to-point movements, or short sequences of discrete movements, in which the full complexity of the dynamics of the system may not yet be fully manifest. A more extended continuous interaction may reveal more of the challenges arising from complex underactuated dynamics. For instance, when a system is near an antiresonance frequency, its evolution is very sensitive to small changes in the input, rendering the behavior of the system chaotic and essentially unpredictable in the longer term. Such small perturbations readily arise from the fact that human movements are intrinsically variable. This presents a problem for the widely held assumption that humans rely on internal models of the manipulated object to select and execute a movement policy (Danion et al. 2012; Dingwell et al. 2002; Flanagan et al. 2006). How can humans learn an internal model of a complex underactuated object that has a potentially unpredictable temporal evolution? How can humans control the behavior of such objects? Relying on feedback control is largely insufficient for the manipulation of objects with complex dynamics due to neural transmission delay. Despite these challenges, humans skillfully manipulate complex objects of all degrees of complexity. How humans achieve this is an open question.

Extending previous work by Sternad and colleagues (Bazzi et al. 2018; Hasson et al. 2012a; Nasseroleslami et al. 2014; Sternad and Hasson 2016), this paper investigates continuous manipulation of an underactuated object with nonlinear internal dynamics. The task of moving a bowl-shaped cup with a ball inside was implemented in a virtual environment, using a cart-and-pendulum model to mimic the ball rolling in the moving cup. Notably, one of our (Nasseroleslami et al. 2014) previous studies demonstrated that the continuous evolution of this system shows features of deterministic chaos. With the use of mathematical modeling and simulation of the task dynamics, this previous study examined the strategy that humans adopt when manipulating this complex object in continuous rhythmic fashion. Moving at an imposed frequency, participants chose movement amplitudes that made the interaction easier to predict. Counter to expectation, interaction force and smoothness were not minimized.

The present study examined the same task but extended the question in two ways. First, rather than imposing a frequency for the oscillatory movement, the present study prescribed the movement amplitude, leaving frequency free to choose. The task of choosing a frequency gave rise to new behaviors and new questions because the resonance structure of the system may now play a significant role in the choice of strategy. Second, we extended the modeling of human control by including the mechanical impedance of the hand. The previous study on the same system only considered the dynamics of the cart-and-pendulum system (Nasseroleslami et al. 2014). However, the object is in continuous interaction with the human, whose neuromechanical properties are likely to influence the cart-and-pendulum dynamics. Therefore, this study introduced a simplified model of hand mechanical impedance interacting with the cart-and-pendulum system.

Several studies on unconstrained movements have demonstrated that humans tend to move in a way that minimizes physical effort (e.g., Alexander 2000; Prilutsky and Zatsiorsky 2002). Extending these findings to the manipulation of complex underactuated objects, our first hypothesis is that humans seek to minimize the effort or specifically the interaction force. We assessed this hypothesis by quantifying the root-mean-square value of the interaction force between the object and the hand. However, although demonstrated for free movements, this principle may become less prominent when the manipulated object presents additional challenges, specifically when it develops increasingly erratic behavior that becomes hard or impossible to predict. Therefore, we also tested the hypothesis that humans adopt strategies that make the hand-object interaction more predictable (hypothesis 2). When interactions are predictable, it is easier for humans to anticipate the object motion and hence the force arising from the internal dynamics of the object. Anticipating this “perturbing” force, subjects can directly generate the appropriate interaction force to achieve the desired movement. Conversely, unpredictable object behavior requires continuous correction and adaptation of the hand movement, which may be tiring, both physiologically and cognitively. Predictability of the object dynamics may, therefore, obviate computational effort and afford simpler internal models to guide feedforward control. We assessed predictability by quantifying mutual information between the hand-cup interaction force and the object kinematics.

Addressing hypotheses 1 and 2 rendered insight into human movement strategies (what do humans optimize), but they did not inform how humans achieved these strategies. Such explanation required closer analysis of the object dynamics. Numerous studies on rhythmic movements have provided evidence that resonance properties of the limbs or the object influence behavior. For example, in walking, the preferred stepping frequency maps onto the resonance frequency of the leg modeled as a simple pendulum (Holt et al. 1990). A study of infants in a “jolly jumper” showed that infants tune into the resonance frequency of the jolly jumper (Goldfield et al. 1993). Rhythmically swinging handheld pendulums of different mass and length has demonstrated that humans have a tendency to oscillate at the natural frequency of the hand-pendulum system (Yu et al. 2003). One main advantage of moving at the resonance frequency is its energetic efficiency: in oscillatory systems at resonance, the ratio between the amplitude of the movement output and the force input is maximal. Another feature of oscillating at resonance has been shown by Goodman et al. (2000) in a study on rhythmic limb movements. Time series analysis using phase space embedding revealed that the trajectories became more predictable when oscillating at resonance. However, that study focused on pendular limb movements, and the applicability of its findings to the manipulation of underactuated objects is unclear. We, therefore, tested an additional hypothesis that in complex underactuated object control, humans exploit the resonance structure of the manipulated object (hypothesis 3). As the analyses showed, the manipulated object together with the hand had not only one, but also a second resonance frequency separated by an antiresonance frequency, a structure that will aid in interpreting the results.

In the experiment, participants manipulated a virtual cart-and-pendulum system at their preferred frequency with the movement amplitude prescribed. To evaluate the strategies that humans adopt, we mathematically examined the cart-and-pendulum system coupled to a simple model of hand impedance. This model-based analysis allowed us to assess alternative execution strategies, i.e., different values of frequency and hand impedance that could be used to perform the task. Interaction forces and the degree of predictability were calculated both experimentally and in simulation. Comparison of human behavior with the mathematically derived results showed that participants did not minimize interaction force but favored strategies with high predictability. In addition, frequency analysis of the coupled object-hand system showed that the degree of predictability was closely related to the resonance and antiresonance frequencies of the system.

EXPERIMENTAL PROCEDURES

Participants

Ten young adults with no self-reported neuromuscular pathology volunteered for the experiment (mean age = 24.3 ± 1.8 yr). All participants performed the task with their dominant hand. They were naïve to the purpose of the study and gave written, informed consent before the experiment. All procedures were approved by the Northeastern University Institutional Review Board.

Virtual Task

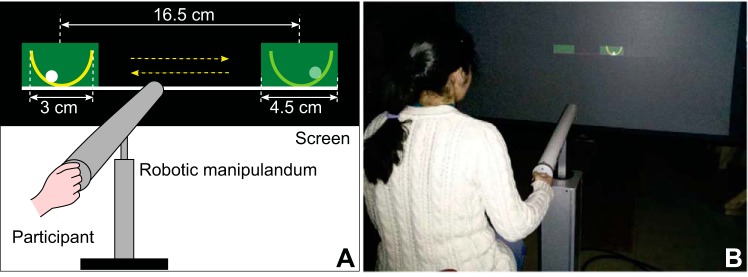
To test the three hypotheses, a virtual task mimicking the manipulation of a bowl-shaped cup with a ball inside was developed. Importantly, this system is underactuated, since moving the cup causes movements of the ball, which simultaneously exerts forces on the cup: the person moving the cup has to take into account these indirectly controlled forces to obtain the desired movement of the cup. A simplified model of a cup-and-ball was simulated in a virtual environment with visual and haptic feedback via a robotic manipulandum. Participants were asked to move this virtual cup rhythmically between two specified targets but were allowed to choose their preferred frequency.

Mechanical Model

Similar to Hasson et al. (2012a, 2012b), Nasseroleslami et al. (2014), and Sternad and Hasson (2016), the cup-and-ball system was modeled as a ball sliding in a semicircular cup (Fig. 1A). The cup motion was limited to one direction in the horizontal plane, without any friction. Under the assumption that the ball does not roll but only slides without friction between the cup and ball, the cup-and-ball system was mathematically equivalent to an undamped pendulum attached to a moving cart (Fig. 1B). The ball corresponded to the pendulum bob, the horizontal position of the cup corresponded to the cart position, and the arc of the cup corresponded to the semicircular path of the pendulum. With this simple model, the full dynamics of the task could be computed more easily, without sacrificing the essential elements of the dynamics: underactuated and nonlinear.

Fig. 1.

Model of the task. A: conceptual model of the cup-and-ball system. B: mechanical model of cup-and-ball dynamics as a cart-and-pendulum system.

Hence, the equations of the cart-and-pendulum motion are:

$$\left(m_{\text{c}}+m_{\text{p}}\right)\stackrel{‥}{X}=m_{\text{p}}d[{\dot{\theta }}^2\sin \theta -\ddot{\theta }\cos \theta ]+{\text{F}}_{\text{inter}}={\text{F}}_{\text{ball}}+{\text{F}}_{\text{inter}}$$

$$\ddot{\theta }=-\frac{\ddot{X}}{d}\cos \theta -\frac{g}{d}\sin \theta ,$$ (1)

where X is the cart position, θ is the pendulum angle, F_inter is the force applied by the human on the cart, and F_ball is the force applied by the pendulum (the ball in the conceptual model) on the cart. Parameters of the system are the mass of the cart (m_c), mass of the pendulum (m_p), the pendulum length (d), and the gravitational acceleration (g). The following values were used: m_c = 2.40 kg, m_p = 0.60 kg, and d = 0.45 m. These values were chosen because they rendered resonance and antiresonance frequencies of the system that were well within human motor capacities and within reach of participants. The cart and pendulum masses were chosen to make the object light enough to avoid fatigue. The ratio of cart and pendulum masses was set to make the underactuated internal dynamics a prominent feature, i.e., participants clearly felt the forces generated by the ball. For lighter ball masses, the cart-and-ball system approximated a rigid object.

Apparatus and Data Acquisition

The dynamics of the cup-and-ball system were simulated in a virtual environment (Fig. 2). Participants were seated on an adjustable chair in front of a screen and interacted with the virtual environment via a 3-degree-of-freedom robotic manipulandum (HapticMaster; Motekforce, Amsterdam, Netherlands; van der Linde and Lammertse 2003). The force applied by the participants on the handle of the robotic arm (F_inter in Eq. 1) controlled the position of the virtual cup (X in Eq. 1). The movements of the robotic arm were restricted to horizontal translations parallel to the participant’s frontal plane to ensure a one-dimensional motion of the cup as in the model. Participants felt the interaction force (system inertia and F_ball in Eq. 1) via the force feedback provided by the robotic manipulandum. A custom-written C++ program based on the HapticAPI (Moog FCS Control Systems) computed the ball kinematics and controlled the virtual display as well as the force feedback.

Fig. 2.

Experimental setup of the ball-and-cup task using virtual reality and force feedback. A: rendering of the task in the virtual environment: the robotic manipulandum provided haptic feedback of the mechanical interaction with the object while the behavior of the system was displayed online on the back-projection screen. The physical model used the distances shown on the figure, whereas the distances displayed on the screen were multiplied by a factor of 4 for visibility. The cup displayed was 7.5 times smaller than the physical arc determined by the length of the pendulum. B: participant using the HapticMaster to interact with the simulated cup-and-ball system. The position of the cup was controlled by the force exerted on the robot.

The cup and ball movements were displayed on a 2.40 × 2.40-m back-projection screen located 2.15 m in front of the participants. The display consisted of two green, rectangular targets on a horizontal line delimiting the displacement of the cup; a yellow semicircle represented the cup, and a small, white circle represented the ball (Fig. 2). Although the cup was only displayed as a semicircle, there was no restriction on the ball angle, and the pendular rotations could exceed 90° without the ball escaping the cup. The visual translation of the cup was 4.0 times the physical displacement of the manipulandum. The cup displayed on the screen was 7.5 times smaller than the physical dimension of the cup (set by d) to have plausible dimensions and fit the display. The force applied by the participants on the robotic arm (F_inter), the cup kinematics (position X, velocity Ẋ, and acceleration Ẍ), and the computed ball kinematics (angular position θ, angular velocity θ̇, and angular acceleration θ̈) were recorded at 120 Hz.

Experimental Task and Instructions

Participants were asked to move the cup rhythmically between two targets located at a horizontal distance of 16.5 cm from one another (physical distance between the centers of each target; Fig. 2A). Participants were instructed to place the cup within the target rectangle at each excursion so movement amplitude was prescribed. However, the scaled cup was 3 cm wide, whereas each target was 4.5 cm wide; the peak-to-peak excursion of the physical cup oscillation could, therefore, range from 15 to 18 cm and still satisfy the task. This tolerance gave participants some leeway to develop their preferred motion. Furthermore, participants were told that they could freely choose their frequency of oscillation and that they could change it throughout the experiment to arrive at their most preferred frequency. Even though participants did not receive explicit restrictions on the movement frequency, a demonstration of the task by the experimenter and the emphasis to “move rhythmically” discouraged them from extremely slow movements. Note that people do not necessarily prefer to move as slowly as possible, even though this may save effort (Park et al. 2017; van der Wel et al. 2009). No instruction was given regarding the position of the ball within the cup, but participants were informed that the ball could not escape the cup (i.e., the behavior was that of a pendulum, attached with a string, rather than that of a loose ball). However, due to the haptic feedback provided by the manipulandum, participants could not ignore the movement of the ball: the ball movement affected the cart movement, as in a real system, and participants felt and saw it. Note that this experimental design intentionally refrained from specifying a single optimal task performance but rather aimed to give insight into what participants preferred to do, especially after some exploration and practice.

The experiment consisted of 5 blocks of 10 trials each. Each trial lasted 45 s. The trials within a block were separated by a 15-s pause, and the blocks were separated by a break of several minutes. At the beginning of each trial, the cup was positioned at the center of the left target, and the ball rested at the bottom of the cup.

Data Analysis

As the task could be achieved by multiple solutions, i.e., it had redundancy, we distinguished between execution and the outcome or result of the movement. Performance was quantified by variables that fully described the kinematics of the system, i.e., amplitude and frequency of cart and pendulum, whereas the outcome was quantified by the task or result variables interaction force, predictability, and resonance. Result variables were metrics that explicitly tested the hypotheses.

Task performance and kinematic variables.

The task instructions elicited trajectories close to a sinusoid; therefore, the movements of the cart (cup) were characterized by the amplitude (A_k) and the frequency (f_k) of each cycle k (i.e., each back-and-forth movement). A_k was defined as the half-distance between the minimum and the maximum of the cart position during cycle k. The cart period (T_k) was defined as the time between two successive maxima of the cart position; the oscillation frequency was f_k = 1/T_k. In addition, we quantified the relative phase between the cart and pendulum movements by computing the time lag that maximized the cross-correlation between the time series of the cart position and pendulum angle. The resulting time lag was then converted into relative phase.

To detect the extrema in the cart position, the difference between successive data points, i.e., velocity, was computed. Extrema were detected as those values where the sign changed. To ensure robust detection of the cart extrema, the cart position data were smoothed with a zero-phase-lag, fourth-order, low-pass Butterworth filter with a 3-Hz cutoff frequency. Note that this smoothing was used only for detecting the extrema.

Result variables.

hypothesis 1: minimize interaction force.

The net force required to perform the task was estimated by the root mean square of the continuous interaction force, RMSF:

$$\text{RMSF}\left({\text{F}}_{\text{inter}}\right)=\frac{1}{T}\underset{0}{\overset{T}{{\displaystyle \int }}}{\text{F}}_{\text{inter}}^2\left(t\right)dt,$$ (2)

where T is the duration of the trial. Note that this hypothesis is about the hand-cart interaction force and not the overall force exerted by the participants. In particular, muscular effort was not evaluated.

hypothesis 2: maximize predictability.

Predictability is a mathematical concept that can be operationalized in several ways. We opted to characterize the degree of predictability of the object dynamics by the mutual information between the input and the output of the system, i.e., the cart trajectory and F_inter. Mutual information is an information-theoretic metric that quantifies the statistical dependency between two variables and thereby quantifies how much knowing one of the variables reduces the uncertainty about the other. High mutual information indicates a small degree of uncertainty (Cover and Thomas 2012). In the present context, mutual information quantifies the degree to which the long-term evolution of the interaction force can be expected, i.e., predicted, if the cart trajectory is known. Unlike cross-correlation, which is limited to linear relations between variables, mutual information assesses both linear and nonlinear dependency. It is, therefore, more suitable for this nonlinear system. In particular, mutual information has been commonly used to quantify predictability of weather and climate, which are modeled by chaotic dynamical systems (DelSole 2004; Kleeman 2011).

The cart trajectory, which was close to sinusoidal, was represented by its phase in state space, φ(t) = arctan[Ẋ/(2 π f X)]. The interaction force F_inter(t) was used as defined above. The predictability measure mutual information (MI) was, therefore:

$$\text{MI}\left(\text{φ},{\text{F}}_{\text{inter}}\right)=\iint P\left(\text{φ},{\text{F}}_{\text{inter}}\right)\text{ln}\left[\frac{P\left(\text{φ},{\text{F}}_{\text{inter}}\right)}{P\left(\text{φ}\right)P\left({\text{F}}_{\text{inter}}\right)}\right]d\text{φ}d{\text{F}}_{\text{inter}},$$ (3)

where P denotes the probability density functions for φ(t) and F_inter(t). Mutual information is a dimensionless quantity, and its unit depends on the base of the logarithm that is used. Here, the natural logarithm was used, and the unit of mutual information is the nat.

hypothesis 3: exploit resonance.

Determining the resonance structure of the system requires analytical or numerical analysis of the system dynamics and cannot be inferred from the behavioral data alone. Therefore, hypothesis 3 will be addressed later in the modeling and simulation section.

Data processing.

For all kinematic and result variables, only the data between t = 20 s and t = 40 s of each trial were analyzed to eliminate transients at the beginning and end of the trial. As the experimental data were compared with model simulations described below, trials that significantly deviated from periodicity needed to be excluded as the model assumed periodicity. Hence, when the standard deviation of the oscillation frequency exceeded 10% of its mean, the trial was excluded as this indicated significant deviation from the instructed periodic movements. Similarly, a trial was excluded if the mean cart excursion was <12 or >21 cm, as it did not satisfy the instructed excursion (15–18 cm), even allowing an additional 3 cm of tolerance. These relatively stringent inclusion criteria were adopted in postprocessing only to enable meaningful comparison with the simulation study reported below (the simulation assumed constant movement frequency within a given amplitude range). They were not success/failure criteria for the participants. One participant’s majority of trials did not satisfy these criteria, and his entire data were eliminated from subsequent analysis. From the remaining 450 trials of 9 participants, only 17 trials did not meet these criteria. These 17 trials were not at the beginning of the experiment but distributed across early and late trials. This indicated that the task did not require practice, and performing with periodicity was not a challenge per se.

The data processing and analyses were performed with MATLAB (The MathWorks, Natick, MA) and Gnumeric. The numerical values of the interaction force and predictability estimates for each experimental trial were computed with MATLAB from the experimental trajectories. Mutual information was calculated with the MATLAB MIToolbox 2.1.2. Statistical comparisons were performed using t-tests since the measures were normally distributed (confirmed by Kolmogorov-Smirnov tests).

BEHAVIORAL RESULTS

Task Performance and Kinematic Variables

As a first overview of participants’ performance, Fig. 3 shows the frequencies (f_k) adopted by participants plotted as a histogram. To obtain a sufficiently large number of data, each cycle, i.e., one back-and-forth movement, was a data point. Two distinct strategies were observed: frequencies were concentrated either between 0.4 and 0.7 Hz (low-frequency strategy) or between 0.9 and 1.8 Hz (high-frequency strategy). The low frequencies were densely concentrated with a sharp peak at ~0.65 Hz, whereas the higher frequencies were distributed more broadly. These two strategies were separated by a gap between 0.7 and 0.9 Hz: only very few oscillations had a frequency within this range. Four participants adopted the low-frequency strategy, and four participants chose the high-frequency strategy. One participant used low frequencies for the 1st 35 trials and then switched to high frequencies; his 1st 35 trials were, therefore, put in the low-frequency strategy, and the subsequent trials in the high-frequency strategy. All others were consistent in their choice throughout their 50 trials, excluding the very 1st trials that were exploration.

Fig. 3.

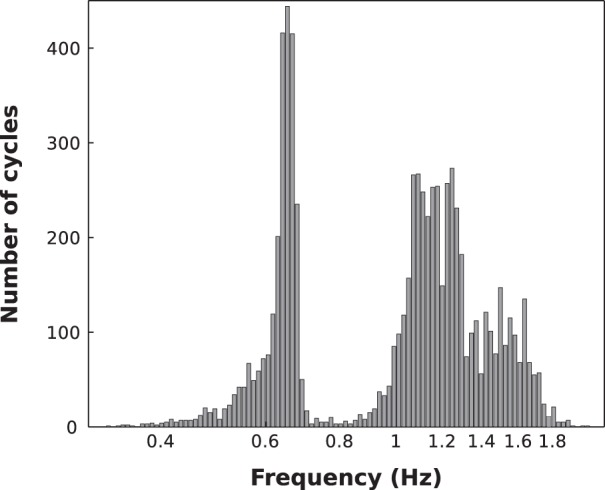
Distribution of frequencies adopted by all participants when manipulating the virtual cup-and-ball system. Histogram represents the frequencies of every single cycle of the 433 valid trials (total: 7,350 cycles). Note that the x-axis is in log scale.

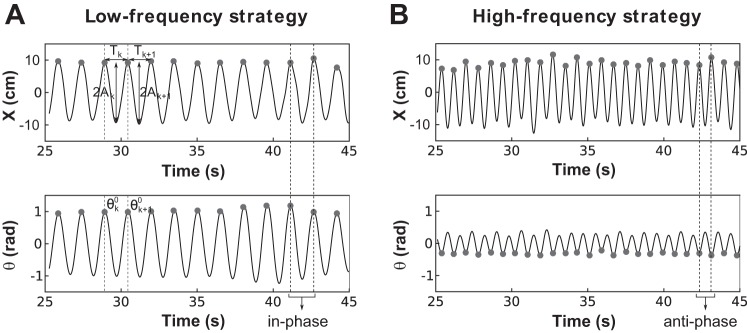
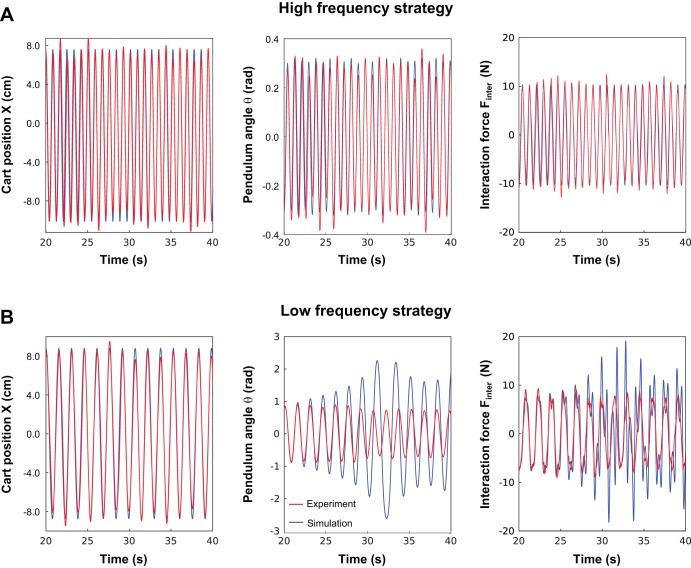
Figure 4 depicts a low- and a high-frequency strategy with exemplary time series of the cart and pendulum positions of two representative participants. For the low-frequency strategy, the cart and pendulum movements were in-phase (the maximum angle of the pendulum was synchronized with the maximum position of the cart). In contrast, the cart and pendulum movements of the high-frequency strategy were in antiphase relation (the pendulum maximum angle was synchronized with the minimum position of the cart).

Fig. 4.

Experimental cart and pendulum trajectories. Representative trajectories of the cart (top) and pendulum (bottom) from 1 participant who chose the low-frequency strategy (A) and 1 participant who chose the high-frequency strategy (B) are shown. With the low-frequency strategy, the cart and pendulum movements were in-phase, and the pendulum oscillations were large. With the high-frequency strategy, the cart and pendulum movements were antiphase, and the pendulum oscillations were smaller. θ, Pendulum angle; A_k, amplitude of each cycle k; T_k, time between 2 successive maxima of the cart position (X).

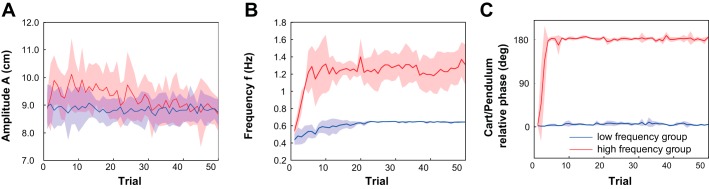
Figure 5 shows how the kinematic variables A and f and the relative phase between the cart and pendulum movements changed over the 50 practice trials for the 2 groups, i.e., 2 strategies. In overview, all kinematic variables tended to show an initial transient and then reached a plateau relatively early on.

Fig. 5.

Evolution across trials of the experimental kinematic variables. A: amplitude (A) of the cart oscillations. B: frequency (f) of the cart oscillations. C: relative phase between the cart movement and the pendulum movement (θ). Note that the amplitude is defined as the half-distance between the cup extrema. Each of the 433 valid trials was represented by 1 single value of A and f and relative phase by averaging across all of the cycles within 20 ≤ t ≤ 40 s in the trial. Blue and red correspond to the 2 frequency groups. Thick lines denote the mean across participants; the shaded areas denote the standard deviations across participants. deg, Degrees.

Cart oscillation amplitude (Fig. 5A).

The amplitude (A) of the cart was relatively invariant throughout the whole experiment in the low-frequency group, whereas for the high-frequency group it only stabilized in approximately the last 20 trials. The mean cart amplitude in the last 20 trials converged to similar values in both frequency groups: 8.8 ± 0.1 cm in the low-frequency group and 8.9 ± 0.1 cm in the high-frequency group. These values were within the instructed amplitude range, although closer to the higher limit, showing that both participant groups satisfied the task. The mean amplitudes over the last 20 trials were not significantly different between groups (P = 0.47).

Cart oscillation frequency (Fig. 5B).

After initial exploration in which all participants adopted relatively low frequencies (~0.5 Hz in the very 1st trials), f stabilized after ~15 trials in both groups. The low-frequency group arrived at a mean movement frequency of 0.65 ± 0.01 Hz (average and standard deviations across the last 35 trials). The high-frequency group adopted a mean movement frequency of 1.27 ± 0.04 Hz (average and standard deviations across the last 35 trials), although the variability across participants was much higher, as already indicated by the broad distribution in Fig. 3. The mean frequencies over the last 35 trials were significantly different between groups (P < 0.01).

Cart and pendulum synchronization (Fig. 5C).

In the low-frequency group, the relative phase between the cart and pendulum movements remained close to 0 for all trials, indicating in-phase movements (average relative phase over all trials: 4.92 ± 2.71°). In the high-frequency group, after abruptly transitioning from 0 to 180° in the 1st 5 trials, relative phase stabilized at ~180°, indicating antiphase movements (average relative phase over the last 45 trials: 181.9 ± 4.47°). No intermediate relative phase values were observed in any of the experimental trials.

Result Variables and Hypothesis Testing

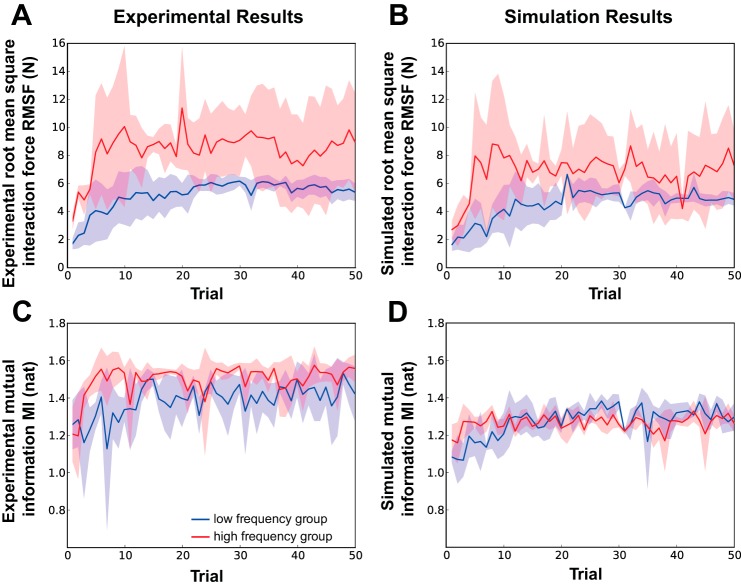
Figure 6, A and C, displays the evolution of the result variables interaction force (RMSF) and mutual information (MI) averaged over all participants across trials. The two frequency strategies are again shown separately. Similar to the kinematic variables, there is an initial change leading to a plateau relatively early. To evaluate the hypotheses, the initial 5 trials were compared with the final 5 trials.

Fig. 6.

Evolution across trials of the result variables. Evolution of the experimental (A and C) and simulated (B and D) result variables root-mean-square interaction force (RMSF) and mutual information (MI) across trials is shown. Experimental variables were computed from the measured time series. Simulated variables were computed from time series obtained by simulation of the coupled model (see main text). Simulations were run using the experimental values of the cart amplitude and frequency. Natural logarithm was used, and the unit of MI is nat. Solid lines represent the average over all participants in each of the 2 frequency groups, and the shaded areas represent 1 standard deviation.

Hypothesis 1: interaction force.

RMSF increased from 2.57 ± 0.56 to 5.49 ± 0.10 N in the low-frequency group and from 5.48 ± 1.59 to 9.09 ± 0.38 N in the high-frequency group between early and late trials. The increase was significant in both groups (P < 0.001). This evolution suggests that participants did not minimize interaction force, counter to hypothesis 1. Instead, with practice they increased the exerted interaction force. Furthermore, five out of the nine participants chose the high-frequency strategy, which was associated with significantly higher RMSF values. If minimization of interaction forces had been the criterion, all participants should have converged to the low-frequency strategy.

Hypothesis 2: predictability.

MI between the interaction force and the cart kinematics of the low-frequency group increased from 1.25 ± 0.05 nat in the 1st 5 trials to 1.44 ± 0.06 nat in the last 5 trials. In the high-frequency group, mutual information increased from 1.36 ± 0.08 to 1.53 ± 0.03 nat between early and late trials. The increase was significant in both groups (P < 0.003), supporting hypothesis 2 that participants sought to increase predictability of the system they interacted with. Note that although the increase in MI seemed modest, the maximum achievable value of MI was ~1.8 nat (for achievable oscillation frequencies). Therefore, the observed relative increases were important.

SIMULATIONS AND ANALYSIS OF THE RESULT SPACE

The results of the behavioral experiment provided support for hypothesis 2 that humans strive to increase the predictability of the interaction when manipulating an inherently erratic or unpredictable system. Conversely, the interaction force was not minimized in this interactive task (counter to hypothesis 1). To evaluate these findings further and to test hypothesis 3, we compared the strategies adopted by participants with possible alternative executions to shed light on priorities in human control. To this end, model simulations were performed to compute the result variables for alternative executions that could have achieved the task.

Coupled Model

In a previous study, the task dynamics were analyzed by considering the behavior of the cart-and-pendulum system alone without including the controlling hand (Nasseroleslami et al. 2014). However, this uncoupled model only partly replicated our experimental data (see appendix a). We, therefore, extended the model to include the continuous coupling between the cart and the hand.

Mechanical model and forward dynamics.

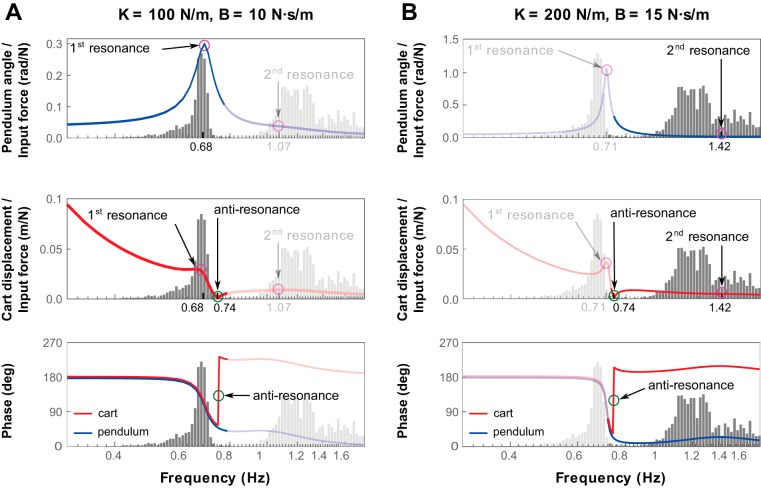
To capture the dynamics of the task more accurately, the cart-and-pendulum system was coupled to the hand dynamics (Fig. 7). The hand dynamics was represented by an ideal force generator (force F_input) in parallel with a spring (stiffness, K) and a damper (damping coefficient, B). F_input(t) was the force required to follow a desired trajectory [X_des(t), Ẋ_des(t)]. If the full dynamics of the task, including the pendulum force, were perfectly anticipated, participants would be able to generate an F_input allowing the cart to follow exactly the desired trajectory X_des(t). In reality, however, it was unlikely that participants learned the perfect model due to the pendulum force acting as a perturbation. Therefore, the motion due to the generated F_input(t) did not exactly track the desired cart trajectory, so that the actual cart trajectory (X) differed from X_des. The spring and damper, which was a simplified model of hand impedance, then served to resist this perturbation. Note that this model represented the impedance at the level of the limb: K and B corresponded to limb features and not to properties of the involved muscles. The equations of motion of the coupled model are

$$\left(m_{\text{c}}+m_{\text{p}}\right)\ddot{X}=m_{\text{p}}d[{\dot{\theta }}^2\sin \theta -\ddot{\theta }\cos \theta ]+{\text{F}}_{\text{inter}}={\text{F}}_{\text{ball}}+{\text{F}}_{\text{inter}}$$

$$\ddot{\theta }=-\frac{\ddot{X}}{d}\cos \theta -\frac{g}{d}\sin \theta$$ (4)

$${\text{F}}_{\text{inter}}={\text{F}}_{\text{input}}-K\left(X-X_{\text{des}}\right)-B\left(\dot{X}-{\dot{X}}_{\text{des}}\right)\mathrm{.}$$

Given the task instructions, the desired trajectory was a sinusoid X_des(t) = A sin(2 π f t + π/2).

Fig. 7.

Model used to analyze the dynamics of the task in simulation. Forward dynamics of the cart-and-pendulum system were coupled to a model of hand impedance. X, cart position; θ, pendulum angle; F_inter, interaction force; F_input, input force; K, hand stiffness; B, hand damping coefficient; X_des, desired cart position; d, pendulum length; m_c, mass of the cart; m_p, mass of the pendulum.

The coupled model was simulated with forward dynamics, i.e., computing the system state variables X(t), Ẋ(t), θ(t), and θ̇(t) and F_inter(t) from a known F_input(t). Since F_input(t) could not be measured experimentally, it was chosen to match the force required to manipulate a rigid object of similar mass, i.e., F_input(t) = (m_c + m_p) Ẍ_des(t). Humans can manipulate rigid objects very accurately, suggesting that they have a good model of the task dynamics. The hand impedance parameters K and B were considered constant during a trial.

Execution Variables

To evaluate the three hypotheses, one must first define a strategy. This was defined by the set of execution variables that participants directly controlled and that fully determined the task outcome (and hence referred to as result variables). While the cart oscillation amplitude (A) was prescribed in the experiment, participants could freely choose three variables of the coupled model: the movement frequency (f), the hand stiffness (K), and the damping (B), referred to as execution variables.

Unlike the movement frequency, the experimental hand stiffness and damping could not be measured directly but had to be estimated to afford forward simulations. To this end, an optimization was conducted that aimed to estimate the values of K and B for which the simulated cart and pendulum trajectories best resembled the experimental trajectories. The optimization process and the cost criterion (C) are detailed in appendix b.

Simulation of Result Variables and Hypothesis Testing

As for the behavioral experiment, the simulation tested the hypotheses by evaluating the result variables root-mean-square interaction force (RMSF; Eq. 2) and mutual information (MI) between the cart kinematics and the interaction force (Eq. 3). To obtain the space of all executions spanned by execution variables f, K, and B, forward dynamics simulation of the coupled model were run to generate the profiles of the cup kinematics φ(t) and F_inter(t). With the use of MATLAB Simulink, the simulation time was 45 s, but only data from 20 ≤ t ≤ 40 s were analyzed to eliminate transients. The two result variables, MI and RMSF, were then calculated with MATLAB as for the experimental data. These results then served to test hypotheses 1 and 2.

To evaluate hypothesis 3 (exploit resonance), a frequency response analysis of the coupled model was conducted in MATLAB. Because of the nonlinearity of the coupled cart-and-pendulum and human hand system, classic frequency response tools could not be used. However, the system could be linearized assuming small pendulum angles. Although this approximation was not valid for all frequencies, the linear analysis allowed further insight into the behavior of the system. In the frequency response analysis, only one of the execution variables, f, was varied, whereas K and B were fixed to typical values: one corresponding to the mean values of K and B adopted by participants in the low-frequency group and the other to the mean values in the high-frequency group (see appendix b for the identification procedure of experimental values of K and B).

SIMULATION RESULTS

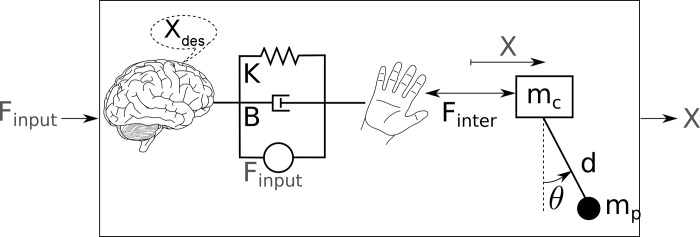
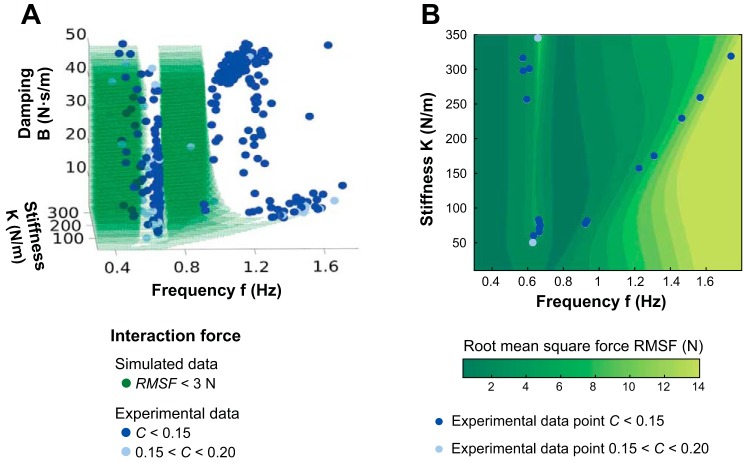
Figures 8A and 9A display the three-dimensional execution space spanned by f, K, and B. For each combination or point in this space, the result variables RMSF and MI were calculated (resolution of f: 0.005 Hz; resolution of K: 2 N/m; resolution of B: 1 N·s/m). The green shades denote the area of low interaction force RMSF (Fig. 8A), and the pink shades denote the areas of high MI or predictability (Fig. 9A), the hypothesized strategies according to hypotheses 1 and 2, respectively. The blue dots are the participants’ data, one point for each trial. Note that the participants’ data points in the two figures are the same to compare them with the two simulated result variables. Figures 8B and 9B show a two-dimensional (2-D) contour map of the same RMSF and MI, plotted for a constant value of B = 10 N·s/m. Hence, this 2-D space only shows a subset of all participants’ data points (for 8 < B < 12 N·s/m). The result space for MI contains one area of very low predictability for frequencies ~0.8 Hz (Fig. 9). This area coincides with an area where the interaction force RMSF is low (Fig. 8); therefore, the two hypotheses of interaction force minimization and predictability maximization are mutually exclusive. Conversely, for frequencies ~0.64 Hz and >1.20 Hz, predictability was high, but the interaction force was high was high as well.

Fig. 8.

Three-dimensional (3-D) plot and 2-D contour map of the root-mean-square interaction force (RMSF) in the space of the execution variables. A: 3-D plot of RMSF in the space spanned by the 3 execution variables frequency (f), stiffness (K), and damping coefficient (B). Green shading represents areas of low interaction force, RMSF < 3 N. B: 2-D map of RMSF in the space spanned by 2 of the execution variables: f and K. Hand damping (B) was fixed at 10 N·s/m. Blue dots represent the strategies (f, K, and B) adopted by participants in the experiment. Dark blue dots correspond to trials for which the impedance fit was good [cost (C) < 0.15, 80% of trials], and lighter dots are trials where 0.15 < C < 0.20 (12% of trials). Trials where the impedance fit was poor (C > 0.20) are not represented since they were not reliable (8% of trials). C is defined in appendix b.

Fig. 9.

Three-dimensional (3-D) plots and 2-D contour map of the mutual information (MI) in the space of the execution variables. Natural logarithm was used, and the unit of MI is nat. A: 3-D plot of MI between the cart trajectory and interaction force in the space spanned by the 3 execution variables frequency (f), stiffness (K), and damping coefficient (B). Pink shading represents areas of high mutual information, MI > 1.2 nat. B: 2-D map of MI in the space spanned by 2 of the execution variables: f and K. Hand damping (B) was fixed at 10 N·s/m. Blue dots represent the strategies (f, K, and B) adopted by participants in the experiment. Dark blue dots correspond to trials for which the impedance fit was good [cost (C) < 0.15, 80% of trials], and lighter dots are trials where 0.15’< C < 0.20 (12% of trials). The trials where the impedance fit was poor (C > 0.20) are not represented since they were not reliable (8% of trials). C is defined in appendix b.

Hypothesis 1: interaction force.

As seen in Fig. 8A, very few experimental trials overlapped with low RMSF solutions that separated the two frequency groups. Very few trials were centered in the low interaction force/low predictability area, and two of these data points were based on only a moderately good impedance fit (light blue dots). The 2-D section in Fig. 8B shows the modulation of RMSF for different frequency and stiffness combinations. Notably, the low interaction force solutions are indicated at movement frequencies <0.5 Hz or between 0.7 and 0.9 Hz. The experimental data points clearly were not in these regions and, therefore, did not support hypothesis 1.

In addition, the simulated time series of the model were analyzed in analogous fashion to the experimental time series. The simulated RMSF was computed from time series obtained by simulation of the coupled model initialized with the experimental values of the execution variables. Figure 6B displays the evolution across trials of the simulated RMSF averaged over all participants in each of the two frequency groups. The significant increase in RMSF from early to late trials in both groups was a further indicator that low interaction force was not a priority. The simulated RMSF increased from 2.35 ± 0.51 to 4.89 ± 0.07 N in the low-frequency group and from 4.42 ± 1.89 to 7.44 ± 0.58 N in the high-frequency group (P < 0.001). Note that despite some discrepancies between the experimental and simulated RMSF, the general trends in their evolution and even the magnitudes were remarkably similar, supporting the adequacy of the coupled model and the estimated values of K and B.

Hypothesis 2: predictability.

According to Fig. 9A, none of the participants chose a strategy located in the area of lowest MI, i.e., low predictability (nonshaded areas). The two frequency groups were clearly separated by the low MI area ~0.8 Hz. Figure 9B details the irregular pattern of MI for different frequency-stiffness combinations, with adjacent regions of high and low MI between 0.6 and 0.8 Hz. This fast change in MI was likely due to the resonance structure of the system detailed below. The more intricate variation of MI at higher frequencies might be due to chaotic behavior. The data suggest that participants adopted strategies with relatively high MI, i.e., high predictability.

Additionally, MI was computed from the time series of the simulated data and is presented in Fig. 6D. MI increased from 1.11 ± 0.05 nat in the early (1st 5) trials to 1.30 ± 0.03 nat in the late (last 5) trials in the low-frequency group (P = 0.003). In the high-frequency group, the simulated MI increased from 1.21 ± 0.07 to 1.29 ± 0.02 nat (P = 0.02). Again, note that the maximum value of MI was ~1.8 nat. Comparing this progression with the experimental values (Fig. 6C) shows that both the time course and the magnitudes of the MI simulated values were close to the experimental values, supporting the adequacy of the coupled model and the estimated values of stiffness and damping. This simulation result strengthens the experimental results that predictability was increased with practice.

Hypothesis 3: resonance.

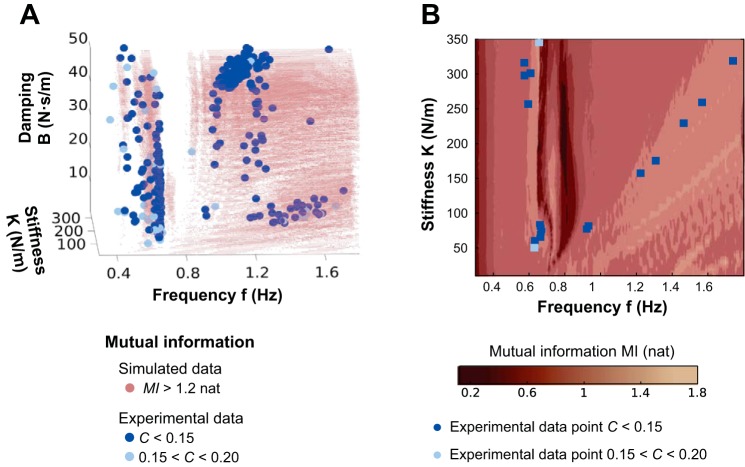
One essential feature of the task dynamics is the resonance structure: the coupled system has two resonance peaks and one antiresonance frequency or dynamic zero between the two resonance frequencies. Figure 10 displays Bode magnitude and phase plots of the linearized coupled model for two representative values of hand impedance. System A was simulated with K = 100 N/m and B = 10 N·s/m, values that were typical for the low-frequency group. System B with K = 200 N/m and B = 15 N·s/m was typical for the high-frequency group. As the responses of the two systems reveal, the resonance peaks depend on the values of K and B. The panels for pendulum angle show one clear resonant peak at 0.68 Hz for system A and at 0.71 Hz for system B.

Fig. 10.

Bode amplitude and phase plots of the linearized coupled model, for different values of hand impedance. A: stiffness (K) = 100 N/m, and damping coefficient (B) = 10 N·s/m, typical for the low-frequency group. B: K = 200 N/m, and B = 15 N·s/m, typical for the high-frequency group. Note that the pendulum amplitude plots have different scales in A and B. Phase plots of the cart and pendulum are superimposed to highlight the synchronization of their movements. For comparison, the gray histogram represents the distribution of frequencies adopted by participants in the experiment (identical to Fig. 3). The part of the graph right (respective left) of the antiresonance frequency is grayed out because it is not relevant for system A (respective B) with values of K and B for which the frequency analysis was performed. deg, Degrees.

Surprisingly, at first sight, the second peaks at the higher frequencies are hardly noticeable. This arises from the fact that the simulation assumed that subjects generated a sinusoidal predictive force F_input(t) intended to produce the desired cart motion X_des(t). This predictive force was based on an incomplete model of the object dynamics that considered only the lowest-frequency mode of behavior, i.e., as though the pendulum and the cart moved as one body, F_input = (m_c + m_p) Ẍ_des. This imperfect predictive force only partially compensated for object dynamics, which was nevertheless sufficient to counteract the resonances of the object, especially at the higher frequencies. Mathematically, the predictive force introduced complex-valued zeros near the complex-valued poles that describe the high-frequency resonance. These zeros tended to cancel or “mask” the effect of the adjacent poles, converting a sharp resonant peak into a broad region of nearly constant magnitude.¹

Importantly, the response of the cup displacement for both systems shows a sharp valley, indicating the antiresonance at 0.74 Hz between the two resonances. Note that the antiresonance frequency is identical in systems A and B, i.e., independent of the values of K and B. The phase plots in Fig. 10 display the relative phase between the input force and the cart movement (red line) and the relative phase between the input force and the pendulum movement (blue line). Comparison between these two curves highlights that for low frequencies the cart and pendulum are in phase, whereas for frequencies higher than the antiresonance frequency, cart and pendulum motions are antiphase. In addition, the relative phase between the input force and the cart movement reveals that for frequencies outside of the two resonance frequencies, the cart movement is antiphase with the input force. Conversely, over a small interval between the two resonance frequencies, the relative phase between the input force and the cart movement is changing.

For comparison of the resonant peaks of the model with the experimental data, the distributions of the observed frequencies in participants are shown in gray (Fig. 10). For the low-frequency group (system A), the peak in the distribution is very close to the resonance peak of the system. For the high-frequency group, participants show a very broad distribution that matches with the smeared-out resonance peak of system B. Comparison between Figs. 9 and 10 reveals that the two resonance frequencies of the system coincided with areas of high MI. This suggests that the behavior of the system is easily predictable when oscillating at a resonance frequency. Conversely, the antiresonance frequency coincides with a region of low MI; therefore, the behavior of the system is hard to predict when oscillating at or around the antiresonance frequency. These results are consistent with hypothesis 3.

DISCUSSION

This study examined strategies that humans adopt when manipulating objects with underactuated internal dynamics. To date, the majority of research in motor neuroscience has examined unconstrained movements in highly controlled experimental tasks to render interpretable data; only relatively few studies have examined control of complex objects. However, everyday behavior is full of complex manipulations that set humans apart from primates and other animals. The present study focused on continuous physical interaction with a cart-and-pendulum system, representing the simplified dynamics of moving a cup of coffee. Participants had to move with a prescribed amplitude but could choose their preferred frequency. Importantly, in continuous interaction with the complex object, the dynamics of this system is underactuated and can exhibit erratic and unpredictable behavior. Such unpredictable dynamics poses significant challenge to any internal model guiding the goal-directed manipulation.

With the use of both behavioral data and numerical analysis of the cart-and-pendulum system coupled to a model of hand impedance, we tested three hypotheses: humans minimize the interaction force required to move the system (hypothesis 1); alternatively, they maximize predictability of the system behavior (hypothesis 2); and/or they exploit the resonance structure of the system (hypothesis 3). Interaction force between hand and cart was quantified by its root-mean-square value. Predictability was operationalized by the mutual information between the kinematics of the cart and the interaction force. Exploiting resonance was tested by comparing the chosen frequencies with the resonance structure of the system. Results of the experiment showed that participants increased, not decreased, the interaction force (counter to hypothesis 1), whereas they increased predictability of the system with practice (consistent with hypothesis 2). Half of the participants chose a strategy that had significantly higher interaction forces while affording similarly high degree of predictability.

The results of the simulations gave further support that, among alternative strategies (defined by values of movement frequency and hand impedance that humans could adopt), participants chose strategies with high predictability but not with low interaction force. These results corroborate and generalize those obtained by Nasseroleslami et al. (2014) in a similar experiment that prescribed movement frequency but left amplitude free to choose. In addition, frequency response analysis of the linearized coupled system showed that participants chose movement frequencies close to the resonance frequencies of the system while avoiding the antiresonance frequency (consistent with hypothesis 3). These findings demonstrate that predictability is a control priority in complex underactuated object manipulation, which takes precedence over principles such as interaction force minimization. The fact that results support both hypotheses 2 and 3 suggests that predictability may be explained by the resonance structure of the system. Therefore, manipulation of underactuated objects cannot be understood simply by extending principles of free movements or rigid object manipulation; underactuated object manipulation constitutes a different class of tasks with different control challenges.

Assumptions of the Coupled Model

To provide an entry to a quantitative understanding of this complex task, an essential element in our approach was simulation of the task dynamics with only minimal assumptions about the controller. We, therefore, coupled a simplified model of hand impedance to the cart-and-pendulum system. This coupled model approximated the experimental data more accurately than a previous model with the cart and pendulum alone (appendix a). However, as this model went beyond the physics of the task alone and included the human controller, certain assumptions had to be made.

Invariance of input force.

One first assumption was that the input force (Eq. 4) was equal to the force required to move a rigid object of the same mass as the cart-and-pendulum system; furthermore, the amplitude, frequency, and phase of this input force was the same sinusoidal signal during and across trials. Although this is a reasonable initial assumption, it is likely that humans learned to adapt their input force based on the perceived interaction force and/or the cart displacement. As the simulation kept the input force invariant, the desired cart trajectory was not always accurately tracked, especially when the hand impedance was low. A plausible next modeling step would be to modulate the amplitude of the sinusoidal input force based on the difference between the actual and desired cart amplitude. Even though it is relatively straightforward to include such an adaptation of the input force, this would evidently make the model more complex and not necessarily help to understand the data.

Invariance of hand impedance.

A second simplifying assumption was that the hand impedance was constant throughout one trial. Given the task instruction and the virtual display, the amplitude of the cart movement was the main concern for participants, whereas the actual trajectory between the two targets was secondary. Therefore, it could be speculated that participants may increase their arm impedance close to the targets to ensure accuracy in the amplitude but decrease impedance during translation between targets. A sinusoidally changing impedance might, therefore, better match experimental data. However, as with the modulation of input force, the potential gain in realism would be at the cost of more parameters to identify. Therefore, constant impedance and constant input force is a reasonable compromise between accurate replication of experimental data and transparency of the model.

Predictability, Muscular Effort, and Antagonist Cocontraction

The simulations reveal that high predictability and low interaction force are nonoverlapping strategies, and the data provide evidence that it is predictability that determines the choice of control strategy. The finding that humans do not try to minimize interaction force may seem to run counter to many studies on unconstrained movements that have shown that humans favor energy- or effort-efficient strategies (Alexander 2000; Nelson 1983; Prilutsky and Zatsiorsky 2002). It should be pointed out that our force criterion only quantified the net external force, i.e., interaction force. Although this external force increased, it might be that higher predictability had a secondary effect on decreasing internal muscular effort: when the system dynamics are erratic, it is difficult to anticipate and preempt the perturbing force of the pendulum by feedforward control. The user may then rely on his/her hand impedance to reject these perturbations and maintain the desired cart trajectory. This requires increasing the impedance through coactivation of antagonist muscles, which results in higher muscular effort without any consequences on the net external force. Conversely, predictable object dynamics may enable participants to anticipate the perturbing interaction force and thereby reduce effort due to cocontraction. Predictability can, therefore, afford a way to minimize the overall muscular effort.

The strongest evidence that force minimization was not an objective was that half of the participants chose the high-frequency strategy associated with higher forces than the low-frequency strategy (Fig. 6). If effort were the main concern, all participants should have chosen the lower frequency and lower impedance (appendix b). As mutual information was similar in both frequency groups, the low-frequency solution would have decreased the overall effort and reconciled the predictability and interaction force objectives. However, one point to note is that the task required only relatively low forces, which may be one reason why optimizing effort was not a priority. Testing the same experiment with different masses for the cart-and-pendulum system is a direction for future work.

Predictability, Error Correction, and Computational Cost

Another factor that may have influenced participants’ choices was that the low-frequency strategy was close to the boundary of the low predictability zone (starting around 0.7 Hz in Fig. 9) compared with the high-frequency solution that was more robust or tolerant to variation in frequency. With the low-frequency strategy, small variations could easily lead to erratic behavior and perturbations that require correction. If such error corrections were executed by the central nervous system, then the computational cost would increase. Computational effort has been recognized and included as a cost in several optimization studies (Ronsse et al. 2010; Todorov and Jordan 2002). However, in these modeling approaches, computational cost terms have remained unspecified placeholders for unaccounted factors contributing to human control choices. A series of studies by Sternad and colleagues have argued that the human controller may exploit the stability properties of a task to avoid computationally expensive corrections (Sternad 2017). With the task of rhythmically bouncing a ball with a paddle, several experiments provided robust evidence that human subjects learned to attain dynamic stability, such that small errors passively decayed, obviating the need for explicit corrections (de Rugy et al. 2003; Schaal et al. 1996; Sternad et al. 2001). When applying larger perturbations, additional corrections were evidenced, although the signature of dynamic stability was still visible (Siegler et al. 2010; Wei et al. 2007, 2008). In a similar spirit, mathematical and empirical studies of a throwing task showed that humans seek solutions that are tolerant to error and noise, therefore, requiring fewer corrections (Cohen and Sternad 2009; Sternad et al. 2011, 2014). Predictability of the interactive dynamics of complex object manipulation may again be a manifestation of human controllers seeking to simplify the control task.

Resonance/Antiresonance Structure, Effort, and Predictability

Did participants choose to move at resonance peaks to reduce effort? As Fig. 10A shows, participants who moved the cart and pendulum in phase could take advantage of the low-frequency resonance to reduce effort but had to exert precise control of frequency to avoid the nearby antiresonance frequency. Participants who chose the antiphase strategy expended more muscular effort due to the higher frequency of antiphase motion and to the elevated stiffness and damping they exhibited. However, the antiphase motion was available over a much broader range of frequencies (Fig. 10B) and, therefore, required much less precise control of frequency. Furthermore, they were far away from the antiresonance frequency or dynamic zero at 0.74 Hz.

Did participants prefer certain cup frequencies because they were associated with specific relative phases between the cart and the pendulum movements or between the input force and the cart movement? Several studies on rhythmic bimanual coordination have shown that humans prefer in-phase and antiphase relations between two limbs over other phase relations (Kelso 1984; Schöner and Kelso 1988; Sternad et al. 1992, 1996). In the present experiment, participants also oscillated the cart either in-phase (at low frequencies) or antiphase (at high frequencies) with the ball movements and avoided intermediate relative phases at the antiresonance frequency. However, this observation does not imply that participants chose strategies for their relative phase values. Except at antiresonance, the task dynamics did not allow other relative phases as the frequency response plots show (Fig. 10). The entire frequency range <0.65 Hz corresponds to in-phase coupling, but participants of the low-frequency group nevertheless all converged to a narrow area of high predictability (Fig. 9). Similarly, the high-frequency group favored those subsets of the frequency range with high predictability. In addition, a large set of frequencies outside of the two resonance frequencies correspond to antiphase coupling between the input force and the cart movement (red line in Fig. 10). It is reasonable to think that participants may prefer this antiphase coupling between what they predict (input force) and what they actually obtain (cart movement) over any other relative phase. Indeed, antiphase coupling between force and movement is what one gets in the very common situation of manipulating a rigid object. However, if relative phase were the only concern, participants’ data points would be spread over all of the frequencies with antiphase coupling and not grouped over a narrow frequency range. These observations support that potential phase preferences alone do not account for our observations.

Why did participants avoid the antiresonance frequency? At antiresonance, the force generated by the pendulum movement (F_ball in Eq. 4) exactly opposes the interaction force exerted by the human (F_inter in Eq. 4), resulting in zero displacement of the cart. In addition, near the antiresonance frequency, the relation between cart motion and input force undergoes a large and rapid, almost discontinuous, phase shift, whereas the relation between pendulum motion and input force does not (phase plot in Fig. 10). Around the antiresonance frequency, the oscillations of the cart and pendulum desynchronize very quickly and small variations result in large changes in the direction of the perturbing force due to pendulum motion. This makes the compensatory input force that should be applied to obtain the desired cart movement hard or impossible to predict. The results clearly showed that subjects consistently avoided the antiresonance frequency and, implicitly, favored predictability.

Task-Dynamic Approach, Internal Models, and Predictability

Most computational studies on movement control start with a hypothesis about the human controller. For example, several studies of the pole-balancing task investigated specific hypotheses about the neural control system, ranging from different control models to the role of noise or sensory feedback (Gawthrop et al. 2013; Insperger et al. 2013; Mehta and Schaal 2002; Milton 2011; Milton et al. 2013; Venkadesan et al. 2007). In contrast, our task-dynamic approach shifted the emphasis to understand first the task and its affordance while minimizing assumptions about human neuromotor control (Sternad 2017). Starting with a mathematical model of the task and analysis of its dynamics, the solution space can be derived and human solutions can be evaluated. To make this mathematical approach transparent, a simplified model is advantageous. Here, we reduced the fluid dynamics of the coffee to a single degree of freedom. As with any virtual implementation, this may raise the question whether the problem has become too simple and whether the results will generalize to the real cup of coffee. Recently, two theoretical studies have indeed analyzed the cup of coffee system in its full physical complexity (Han 2016; Mayer and Krechetnikov 2012). Comparison of these and our studies may reveal the advantages and disadvantages of the realistic vs. computationally simplified approach.

Our task-based approach does not contradict but complements controller-based approaches. When, for example, Nagengast et al. (2009) studied optimal control for the manipulation of a virtual mass-spring-damper system, they assumed that participants had complete knowledge of the system dynamics. Similarly, Dingwell et al. (2002, 2004) showed that participants manipulating a linear mass-spring system displayed behavior compatible with learning an internal model of the object dynamics. However, underactuated objects, such as our cup-and-pendulum system, pose a significant challenge due to their possibly unpredictable dynamics, leading to an apparent absence of correlation between the human action and the resulting behavior of the system. Increasing the predictability of object dynamics might, therefore, be a way to increase the chance of acquiring an internal model.

GRANTS

D. Sternad was supported by the National Institutes of Health Grants R01-HD-087089, R01-HD-081346, and R21-DC-013095 and the National Science Foundation Grants NSF-NRI 1637854 and NSF-EAGER-1548514. N. Hogan was supported by NIH Grant R01-HD-087089, National Science Foundation Grants NSF-NRI 1637814 and NSF-EAGER-1548501, and the Eric P. and Evelyn E. Newman Foundation. P. Maurice was supported, in part, by the European Union’s Horizon 2020 Research and Innovation Program under Grant Agreement no. 731540.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

D.S. conceived and designed research; P.M. performed experiments; P.M. analyzed data; P.M., N.H., and D.S. interpreted results of experiments; P.M. prepared figures; P.M. and D.S. drafted manuscript; P.M., N.H., and D.S. edited and revised manuscript; P.M., N.H., and D.S. approved final version of manuscript.

APPENDIX A: LIMITATIONS OF A MODEL WITHOUT HAND IMPEDANCE

In a previous study, the dynamics of the cup-and-ball task was analyzed by looking at the behavior of the cart-and-pendulum system alone without the controlling hand (Nasseroleslami et al. 2014). This uncoupled model is depicted in Fig. A1, and the motion of the system is described solely by Eq. 1. It is straightforward to simulate this uncoupled model using inverse dynamics calculations: if the cart trajectory X(t) and initial conditions of the cart and pendulum (X₀, Ẋ₀, θ₀, and θ̇₀) are given, the pendulum trajectory θ(t) and the interaction forces F_inter(t) can be computed using Eq. 1 and a numerical integration scheme for θ. This uncoupled model has the advantage that it does not require any assumptions about control by the human (contrary to the coupled model). The only assumption is about the movement of the cart, which could reasonably be modeled by a sinusoid X(t) = A sin (2 π f t + π/2) given the task instructions.

Fig. A1.

Model of the dynamics of the task. Inverse dynamics model of the cart-and-pendulum system alone are shown. θ, Pendulum angle; d, pendulum length; F_inter, interaction force; m_c, mass of the cart; m_p, mass of the pendulum; X, cart position; Ẋ, cart velocity; Ẍ, cart acceleration.

A first approach used this simple model to analyze the task in this work. To test to what degree this model faithfully reproduced human behavior, we ran inverse dynamics simulations to compute θ(t) and F_inter(t). A separate simulation was run for each experimental trial based on X(t) and initial conditions taken from experimental values of X₀, Ẋ₀, θ₀, θ̇₀, and cart amplitude (A) and frequency (f). This afforded direct comparison of the experimental and simulated trajectories of cart and pendulum and the interaction forces. The cart initial conditions X₀ and Ẋ₀ were fixed by the assumed sinusoidal shape of X(t): X₀ = A and Ẋ₀ = 0. Although all experimental trials started with the same nominal conditions (immobile pendulum at 0° angle), trials contained a transient before participants settled onto their approximate steady state with their chosen frequency. Initial transients were excluded because the oscillation frequency varied substantially during this stage. Therefore, the values of A, f, and pendulum initial conditions θ₀ and θ̇₀ were the experimental averages across all cycles within 20 ≤ t ≤ 40 s, as in the experimental data analysis. The simulated cart, pendulum, and force profiles were then compared with the experimental time series of the corresponding trial. A simulation was run for each of the 433 experimental trials with their respective values.

Figure A2 displays one representative example of cart and pendulum trajectories X(t) and θ(t) and the interaction force F_inter(t) from the two frequency strategies. For the high-frequency strategy, all three simulated time series (cart position, pendulum angle, and interaction force) closely matched their experimental counterparts. For the low-frequency strategy, the experimental cart trajectory closely resembled the simulated trajectory, but the pendulum trajectory and the interaction force diverged after a few cycles. The experimental profiles were close to periodic, whereas the simulated profiles differed at each oscillation, developing complex, erratic (possibly chaotic) patterns.

Fig. A2.

Comparison of experimental and simulated trajectories and force time series for the uncoupled model. Experiment (red) and simulation (blue) profiles of the cart trajectory, pendulum trajectory, and interaction force for 1 trial of each frequency strategy. Experimental data correspond to 1 representative trial in each of the 2 frequency strategies. Simulation data were computed from inverse dynamics of the uncoupled model, initialized with the experimental values of amplitude (A), frequency (f), initial pendulum angle (θ₀), and initial pendulum velocity (θ̇₀). A: high-frequency strategy (A = 8.9 cm, f = 1.182 Hz, θ₀ = −0.31 rad, θ̇₀ = −0.05 rad/s). B: low-frequency strategy (A = 8.8 cm, f = 0.655 Hz, θ₀ = 0.79 rad, θ̇₀ = −0.08 rad/s).

To quantify the divergence, the root-mean-square (RMS) errors between the experimental and simulated trajectories were computed. Table A1 summarizes RMS error for each quantity X, Ẋ, θ, θ̇, and F_inter, expressed as percentage of its respective maximum value in the corresponding experimental trial. In the high-frequency group, the RMS error was small and fairly consistent across variables (median RMS error ~10% of the variable maximum experimental value), indicating a reasonably good match between the experimental and simulated profiles. This uncoupled model was, therefore, a competent representation of the cup-and-ball task for the high-frequency strategy. With the low-frequency strategy, however, the RMS error varied greatly and reached 30% of the maximum value for the experimental pendulum angle and angular velocity (and interaction force to a lesser extent). These discrepancies between experimental and simulated data demonstrate that the uncoupled model did not represent the execution strategies adopted by the low-frequency group sufficiently accurately.

Table A1.

RMS error between experimental and simulated trajectories and force time series for the uncoupled model

	Low-Frequency Group		High-Frequency Group
	Median	IQR	Median	IQR
$\frac{\text{rms}\left(X^{\text{e}}-X^{\text{s}}\right)}{{\Vert X^{\text{e}}\Vert }_{\infty }}$	0.10	0.04	0.08	0.02
$\frac{\text{rms}\left({\dot{X}}^{\text{e}}-{\dot{X}}^{\text{s}}\right)}{{\Vert {\dot{X}}^{\text{e}}\Vert }_{\infty }}$	0.13	0.06	0.08	0.03
$\frac{\text{rms}\left({\theta }^{\text{e}}-{\theta }^{\text{s}}\right)}{{\Vert {\theta }^{\text{e}}\Vert }_{\infty }}$	0.29	0.52	0.13	0.09
$\frac{\text{rms}\left({\dot{\theta }}^{\text{e}}-{\dot{\theta }}^{\text{s}}\right)}{{\Vert {\dot{\theta }}^{\text{e}}\Vert }_{\infty }}$	0.31	0.39	0.11	0.07
$\frac{\text{rms}\left({\text{F}}_{\text{inter}}^{\text{e}}-{\text{F}}_{\text{inter}}^{\text{s}}\right)}{{\Vert {\text{F}}_{\text{inter}}^{\text{e}}\Vert }_{\infty }}$	0.22	0.29	0.12	0.04

Ratio of root-mean-square (RMS) error between experimental and simulated data normalized by the maximum value for the cart and pendulum trajectories and interaction force in both subject groups. Simulated data were obtained from inverse dynamics simulation of the uncoupled model. Median and interquartile range were computed over all 433 valid trials. θ, Pendulum angle; θ̇, pendulum angular velocity; X, cart position; Ẋ, cart velocity; F_inter, interaction force; ^e, experimental; ^s, simulated; IQR, interquartile range.

A likely reason for the divergence between experimental and simulated data is the assumption of a perfectly sinusoidal cart trajectory in the simulations, whereas experimental trajectories exhibited small deviations from this ideal shape. Given the sensitivity of the cart-and-pendulum dynamics to initial conditions, small changes in the participant’s movement could lead to significant changes in the system evolution. These deviations of the experimental cart trajectories from a perfect sinusoid could have two main causes: the intrinsic variability of human movements and the perturbations caused by the internal dynamics of the object. The first cause results from the ever-present human variability: even if the object were rigid or if there were no object at all, humans are unable to repeat the same exact movements. Although present in both frequency strategies, this variability could have different consequences, since the sensitivity of the system to initial conditions is not constant.

The second cause, the perturbation forces created by the pendulum movements, affected the cart trajectory because the human hand is not an ideal position generator. Unexpected pendulum forces disrupted hand and hence cart movement. Although this is again true for both frequency strategies, the cart trajectory was likely less perturbed in the high-frequency strategy because hand movements were faster, which is often associated with a higher hand impedance. Higher impedance would result in better resistance to external perturbations and lower RMS error (Table A1).

Furthermore, F_inter results from two different forces (Eq. 1): one is the cart-and-pendulum inertial force, F_inertia = (m_c + m_p) Ẍ, and the other is the pendulum force, F_ball. The average ratio between the RMS pendulum force and the RMS inertial force (computed for 20 ≤ t ≤ 40 s) was 0.70 ± 0.16 in the low-frequency group and 0.32 ± 0.05 in the high-frequency group (averaged across all trials of all participants in each of the 2 groups). Relative to the expected force (i.e., required to accelerate the total system inertia, similar to the manipulation of a rigid object), the magnitude of the unexpected perturbation (the pendulum force) was thus much higher in the low-frequency group and was, therefore, less likely to be resisted. Hence, the current study included the effect of hand impedance on the dynamics of the cart-and-pendulum system.

APPENDIX B: ESTIMATION OF HAND IMPEDANCE IN THE COUPLED MODEL

Unlike the movement frequency (f), the experimental hand stiffness (K) and damping (B) could not be measured directly but had to be estimated from the human data. To this end, an optimization was conducted that aimed at finding the values of K and B for which the simulated cart and pendulum trajectories most resembled the experimental trajectories. For each combination of K and B, a 45-s forward dynamics simulation of the coupled model was performed and compared with the corresponding experimental trial. The continuous variations in the cart amplitude (A) and/or frequency (f) in the experimental trials were evidently not captured in the simulation as constant desired cart amplitude/frequency was assumed. The simulations used the average experimental values of A and f across all cycles of the trial (20 ≤ t ≤ 40 s) to define the desired trajectory, X_des(t) = A sin(2 π f t + π/2), and the input force, F_input(t) = (m_c + m_p) Ẍ_des(t). However, the average amplitude and frequency were only representative of the experimental trial if they did not vary significantly throughout the trial. This motivated the stringent inclusion criteria in the analysis of the behavioral data.

All combinations of 10 ≤ K ≤ 350 N/m (step size 2 N/m) and 3 ≤ B ≤ 50 N·s/m (step size 1 N·s/m) were tested to find the best fit. The difference between the experimental and simulated trajectories was quantified by the cost (C) of the normalized root-mean-square errors of the four quantities X(t), Ẋ(t), θ(t), and θ̇(t):

$$C=\frac{1}{4}\left[\frac{\text{rms}\left(X^{\text{e}}-X^{\text{s}}\right)}{{\Vert X^{\text{e}}\Vert }_{\infty }}+\frac{\text{rms}\left({\dot{X}}^{\text{e}}-{\dot{X}}^{\text{s}}\right)}{{\Vert {\dot{X}}^{\text{e}}\Vert }_{\infty }}+\frac{\text{rms}\left({\theta }^{\text{e}}-{\theta }^{\text{s}}\right)}{{\Vert {\theta }^{\text{e}}\Vert }_{\infty }}+\frac{\text{rms}\left({\dot{\theta }}^{\text{e}}-{\dot{\theta }}^{\text{s}}\right)}{{\Vert {\dot{\theta }}^{\text{e}}\Vert }_{\infty }}\right],$$ (B1)

where the superscripts s and e stand for simulation and experimental, respectively. Only the data within 20 ≤ t ≤ 40 s were included to avoid confounding by transients (both for experimental and simulated trials).

Although the movement frequency was fixed in the simulations, experimental frequencies were not exactly constant within trials. Such variations of the experimental frequency created a temporal offset between the experimental and simulated trajectories, which could lead to high RMS errors even when the two profiles were similar. To limit this artifact, C was computed cycle by cycle, i.e., the RMS errors were computed for each cycle k by time-aligning the experimental and simulated trajectories of cycle k. Subsequently, they were averaged over all cycles.

Across all trials, the median cost measured for the best impedance fit of each trial was 0.104 with an interquartile range of 0.051. Table B1 gives the ratio between the RMS error between experimental and simulated time series and the maximum experimental value of the corresponding trial for the state variables X, Ẋ, θ, and θ̇ as well as for F_inter. The median value of the RMS error was between 9 and 13% of the maximum value, depending on the variable. Importantly, the error was consistently low in both groups, unlike for the uncoupled model above (see Table A1 in appendix a).

Table B1.

RMS error between experimental and simulated trajectories and force time series for the coupled model

	Low-Frequency Group		High-Frequency Group
	Median	IQR	Median	IQR
$\frac{\text{rms}\left(X^{\text{e}}-X^{\text{s}}\right)}{{\Vert X^{\text{e}}\Vert }_{\infty }}$	0.09	0.04	0.09	0.02
$\frac{\text{rms}\left({\dot{X}}^{\text{e}}-{\dot{X}}^{\text{s}}\right)}{{\Vert {\dot{X}}^{\text{e}}\Vert }_{\infty }}$	0.11	0.05	0.08	0.03
$\frac{\text{rms}\left({\theta }^{\text{e}}-{\theta }^{\text{s}}\right)}{{\Vert {\theta }^{\text{e}}\Vert }_{\infty }}$	0.11	0.07	0.12	0.07
$\frac{\text{rms}\left({\dot{\theta }}^{\text{e}}-{\dot{\theta }}^{\text{s}}\right)}{{\Vert {\dot{\theta }}^{\text{e}}\Vert }_{\infty }}$	0.12	0.07	0.10	0.05
$\frac{\text{rms}\left({\text{F}}_{\text{inter}}^{\text{e}}-{\text{F}}_{\text{inter}}^{\text{s}}\right)}{{\Vert {\text{F}}_{\text{inter}}^{\text{e}}\Vert }_{\infty }}$	0.13	0.05	0.13	0.04

Ratio between root-mean-square error (RMS) between experimental and simulated data and the maximum value for the cart and pendulum trajectories and interaction force. Results are separated for the 2 frequency groups. Simulated data were obtained with forward simulation of the coupled model, using the optimized values of hand stiffness and damping for each trial (i.e., the values for which cost was minimum). θ, Pendulum angle; θ̇, pendulum angular velocity; X, cart position; Ẋ, cart velocity; F_inter, interaction force; ^e, experimental; ^s, simulated; IQR, interquartile range.

The values of hand impedance were different between groups. The comparison of stiffness and damping values between the two frequency groups was performed with a Wilcoxon signed-rank test because the data were not normally distributed. Both K and B were significantly lower in the low-frequency group, with P < 0.0001 each. This is consistent with the known fact that, for a similar task accuracy, limb stiffness usually increases with movement speed.

These results are the basis for characterizing the experimental trials with hand impedance. The coupled model with optimized K and B reproduced experimental trajectory and force time series much more accurately than the uncoupled model (especially for the low-frequency group), thus confirming its better competence to analyze the experimental task.