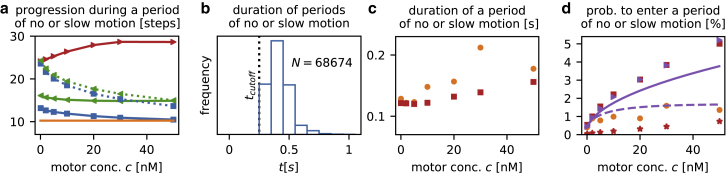
Figure 5.

Periods in which kinesin-1 motors show no or only very slow motion. The model parameters are the same as in Fig. 3. Experimental measurements from Telley et al. (18) are shown in orange. For the detection of these periods, the protocol of Telley et al. (18) was used (see the main text). (a and b) Our model cannot explain the frequent periods of no or slow motion of motors observed experimentally. (a) The distance traveled by a motor between the beginning and end of such a period is shown. A threshold value of d_c = 5 sites (red line) is too large for reliable detection of these periods: motors traverse for almost 30 lattice sites between the beginning and end of such a period, which is three times the experimental result (orange line). This implies that most of the detected events actually reflect stochastically slow motion that is otherwise normal, and hence the scheme detects these events inaccurately with this choice of d_c. Reduction of the threshold to d_c = 3 sites (green) or d_c = 2 sites (blue) leads to results that are in closer agreement with experimental data. However, this correspondence deteriorates on addition of Gaussian noise (σ = 20 nm) to the simulation data before applying the detection protocol (dashed lines). (b) Duration of the thus-detected periods of no or slow motion for c = 20 nM and a detection threshold d_c = 2 sites is shown. In contrast to the experimental findings, in which an exponential distribution was observed, the duration peaks around 0.4 s. This result does not change qualitatively when d_c is varied or Gaussian noise is added at various strengths. (c and d) Qualitative agreement with experiments is found when motors can spontaneously switch between an active and inactive mode at rates extracted from experimental data (18). (c) The duration of periods of no or slow motion detected from simulations of this model variant (red squares) is similar to those measured in experiments (18). The duration was computed by extrapolating the (now) approximately exponential distribution of the detected periods below the cutoff time of 0.3 s (see (18) and the main text for details). (d) The per-step probability that a motor is found in a period of no or slow motion is shown. The direct yield from the detection algorithm (red asterisks) is below experimentally observed (18) values. When their frequency is corrected for the time cutoff (red squares) similar to the procedure used in experiments (18), good qualitative agreement is found, in particular at low motor concentrations. Violet triangles show the frequencies obtained with a different algorithm that counts motors that are inactive or caught up in a traffic jam behind an inactive motor but not motors that move slowly because of their stochastic motion. The good agreement between these results and the original detection protocol (red squares) reveals that spontaneously inactivated motors are the dominant contribution for periods of no or slow motion. Solid and dashed lines show heuristic estimates of the probability of entering such a period, assuming that motors in a traffic jam require two or only one binding site on the lattice. For details, see the main text. To see this figure in color, go online.