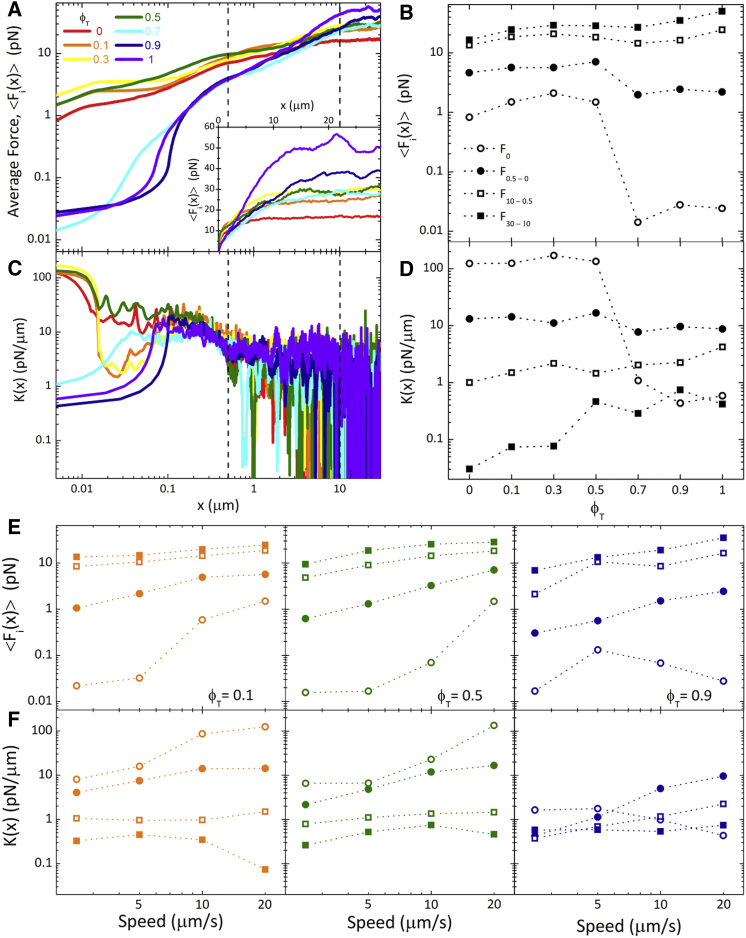
Figure 2.

Mesoscale force response of actin-microtubule composites display a ϕ_T-dependent crossover from strain-softening to strain-stiffening. (A) The ensemble-averaged force <F_i(x)> applied to the moving bead by actin-microtubule composites of varying tubulin molar fraction ϕ_T (listed in legend) is plotted. Data shown are an average over 25 individual (i) measurements. Dotted vertical lines denote the displacements over which <F_i(x)> and K(x) are averaged in (B) and (D). Inset shows <F_i(x)> on a linear scale. (B) The initial <F_i(x)> value, F₀ (open circles), and the average of <F_i(x)> values plotted over different bead displacements, x_f − x_i, denoted as F_xf−xi. Displacements of x_f − x_i = 0.5 − 0 μm (F_{0.5 − 0}, closed circles), 10 – 0.5 (F_10−0.5, open squares), and 30 – 10 (F₃₀₋₁₀, closed squares) are shown. (C) Stiffness, K(x), is calculated as the derivative of the average force with respect to bead displacement (K(x) = d<F_i(x)>/dx). (D) The initial K value, K₀, and the average of K(x) values plotted over different displacements (K_0.5−0, K_10−0.5, K₃₀₋₁₀). Displacements and symbol scheme are the same as in (B). (E and F) The dependence of force and stiffness on the speed of the bead displacement for ϕ_T = 0.1 (orange, left), 0.5 (green, middle), and 0.9 (purple, right) composites is presented. F₀, F_0.5−0, F_10−0.5, and F₃₀₋₁₀ (E) and K₀, K_0.5−0, K_10−0.5, and K₃₀₋₁₀ (F) are shown as a function of bead speed, with the symbol scheme the same as in (B) and (D). To see this figure in color, go online.