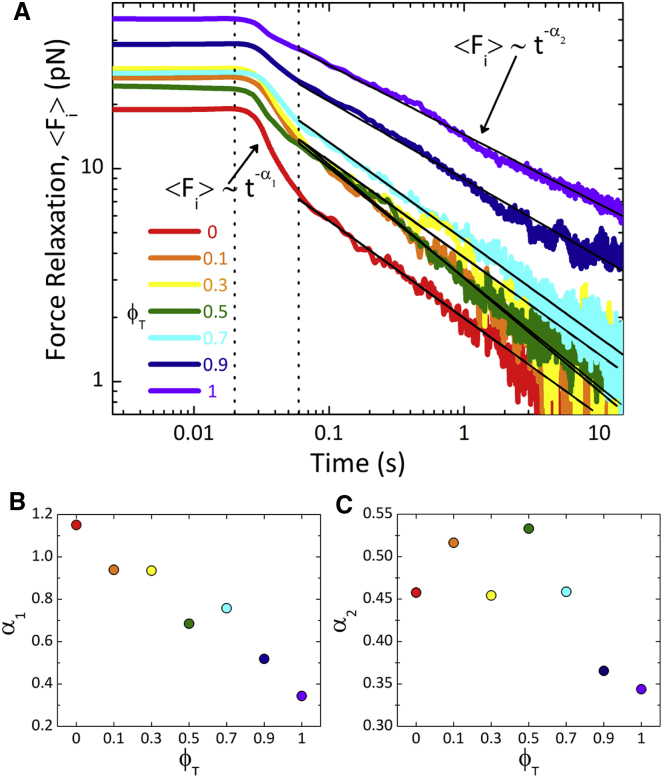
Figure 4.

Force relaxation of actin-microtubule composites exhibits two-phase power-law decay. (A) Relaxation of ensemble-averaged resistive force after bead displacement is shown as a function of time for composites of varying tubulin fractions ϕ_T. The color scheme is the same as in Figs. 2 and 3. Force curves exhibit an initial plateau phase until t₁ ≈ 0.02 s, after which composites relax via two distinct power-law decays: an initial fast decay (<F_i> ∼ t^−α₁) until t₂ ≈ 0.06 s, followed by a slow decay (<F_i> ∼ t^−α₂). Vertical dotted lines indicate the crossover timescales t₁ and t₂. Solid black lines are fits of the data to power laws with exponents α₂. (B) Estimated scaling exponents α₁ for the fast decay, which decrease proportionally with increasing ϕ_T and become indistinguishable from α₂ when ϕ_T = 1, are shown. (C) Scaling exponents α₂ measured for the second decay phase are shown. Exponents exhibit a nonmonotonic dependence on ϕ_T reaching a maximum value of ∼0.53 for ϕ_T = 0.5. To see this figure in color, go online.