Absorption by water increases fluorescence image contrast of biological tissue in the shortwave infrared

Significance

Shortwave infrared (SWIR) fluorescence imaging is a tool for visualizing biological processes deep within tissue or living animals. Our study shows that the contrast in a SWIR fluorescence image is primarily mediated by the absorptivity of the tissue, and can therefore be tuned through deliberate selection of imaging wavelength. We show, for example, that, in 3D tissue phantoms and in brain vasculature in vivo in mice, imaging at SWIR wavelengths of the highest water absorptivity results in the greatest fluorescence contrast. We further demonstrate, in microscopy of ex vivo mouse liver tissue, that imaging at wavelengths of high tissue absorptivity can also increase imaging penetration depth, and use a theoretical contrast model to explain this effect.

Abstract

Recent technology developments have expanded the wavelength window for biological fluorescence imaging into the shortwave infrared. We show here a mechanistic understanding of how drastic changes in fluorescence imaging contrast can arise from slight changes of imaging wavelength in the shortwave infrared. We demonstrate, in 3D tissue phantoms and in vivo in mice, that light absorption by water within biological tissue increases image contrast due to attenuation of background and highly scattered light. Wavelengths of strong tissue absorption have conventionally been avoided in fluorescence imaging to maximize photon penetration depth and photon collection, yet we demonstrate that imaging at the peak absorbance of water (near 1,450 nm) results in the highest image contrast in the shortwave infrared. Furthermore, we show, through microscopy of highly labeled ex vivo biological tissue, that the contrast improvement from water absorption enables resolution of deeper structures, resulting in a higher imaging penetration depth. We then illustrate these findings in a theoretical model. Our results suggest that the wavelength-dependent absorptivity of water is the dominant optical property contributing to image contrast, and is therefore crucial for determining the optimal imaging window in the infrared.

Fluorescence imaging has emerged as a powerful tool for preclinical in vivo imaging and as a promising clinical technology, particularly for surgical guidance (1–6). Most fluorescence imaging approaches use widely available visible (400 nm to 700 nm) and near-infrared (NIR, 700 nm to 1,000 nm) light-emitting fluorophores, which can be detected on high-performing, inexpensive silicon detectors. However, recent advances in longer wavelength detection and synthesis of infrared emitters have also enabled fluorescence imaging in the shortwave infrared (SWIR, 1,000 nm to 2,000 nm). SWIR detection technology, once cost-prohibitive and restricted by military regulations (e.g., the International Traffic in Arms Regulations, in the United States), has become readily available for commercial use and research purposes. With recent progress in InGaAs fabrication, the cost of SWIR cameras has steadily declined, while camera sensitivity and resolution have increased. Moreover, a wide variety of biologically compatible SWIR emitters have emerged, including organic dyes with peak emission in the SWIR (7–10), carbon nanotubes (11, 12), quantum dots (13–15), rare-earth−doped nanocomposites (16), and gold nanoparticles (17). More recently, it was also shown that NIR dyes, which are commercially available and approved for clinical use, can be used for many SWIR imaging applications (18).

Selecting an appropriate imaging wavelength is critical to enabling a given application in biological fluorescence imaging. Fluorophore sensitivity, penetration depth, and spatial resolution all depend on the optical properties of biological tissue, and these tissue properties, including autofluorescence, absorption, and scattering, are each wavelength-dependent. Tissue autofluorescence, which creates interfering background signal, primarily comes from molecules such as NADPH, flavins, and collagen. These molecules emit the majority of light at visible wavelengths and can be avoided by moving into the NIR and SWIR (19). Tissue absorption, which reduces signal intensity, is primarily due to hemoglobin, melanin, lipids, and water. These tissue components each have unique spectral profiles, but share a common absorption minimum between ∼650 nm and 900 nm; thus, the NIR has long been identified as an optimal imaging window for in vivo studies requiring high penetration depths (20–27). Finally, scattering, caused by the refractive index inhomogeneities within most tissues, misdirects photons from the direct path to the detector, degrading spatial resolution and also contributing to signal attenuation. The effects of scattering can be minimized by imaging at the longest wavelengths possible (12).

Considering the combined effects of tissue autofluorescence, absorption, and scattering, the SWIR regime promises greater fluorophore sensitivity, higher tissue penetration depths, and greater spatial resolution than visible and NIR imaging (12, 14, 19, 28–31). For many applications, these improvements are related to an overall increase in image contrast. Studies in 2D tissue-mimicking phantoms predict fluorescent contrast to be the highest between 700 nm and 1,400 nm and between 1,500 nm and 1,600 nm (32), corresponding to the minima in the attenuation spectra of biological tissues (29, 33). Recent demonstrations in vivo, with fluorescence originating from a 3D network of structures, show particularly high contrast between 1,300 nm and 1,400 nm and an additional contrast increase between 1,500 and 1,700 nm (11, 12, 19). However, the effect of small wavelength changes within the SWIR on in vivo image contrast has not been examined.

By probing image contrast with high wavelength resolution, we show that SWIR fluorescence contrast is primarily governed by water absorption in tissue. We investigate the wavelength dependence of contrast in 3D tissue phantoms, disentangling the individual contributions of tissue absorption and tissue scattering, and perform further investigations in vivo in mice. We then describe how different imaging wavelengths in the SWIR influence contrast and penetration depth in microscopy of ex vivo biological tissue and present a theoretical model to illustrate the results. We find, in each case, that images have the highest contrast at wavelengths with the highest water absorption. While these wavelengths have conventionally been avoided to obtain greater signal throughput, we show that in contrast-limited applications, such as tissue with many and/or overlapping fluorescently labeled structures, the improvement in contrast from water absorption enables resolution of deeper structures, resulting in a larger imaging penetration depth. The trade-off between contrast, penetration depth, and fluorescence signal intensity can thus be balanced for a given application by selectively imaging at wavelengths with a particular level of tissue absorption.

Results

Effects of Absorption and Scattering on Contrast in a 3D Tissue Phantom.

We aimed to probe the relationship between tissue scattering, tissue absorption, and fluorescence contrast at SWIR wavelengths. Considering tissue scattering alone, contrast should continuously increase with wavelength, as scattering steadily decreases in accordance with the Mie theory (34). However, tissue absorption, dominated by water in the SWIR, has an unsteady wavelength dependence, exhibiting three local absorption peaks near 970 nm, 1,200 nm, and 1,450 nm with increasing respective intensity. The dominant mechanism of contrast improvement can therefore be revealed if the contrast is probed with sufficiently high wavelength resolution.

We probed the individual influence of absorption and scattering on fluorescence contrast through 3D liquid tissue phantoms. Phantoms were composed of 1% Intralipid in water (H₂O) or 1% Intralipid in deuterium oxide (D₂O). The H₂O-based phantom attenuates light through both scattering and absorption, while the D₂O-based phantom exhibits approximately equal scattering properties but has no absorption in the SWIR (Fig. 1A and SI Appendix, Fig. S1A). Thus, the D₂O phantom was used to measure the influence of scattering alone on contrast, while the H₂O phantom revealed the influence of scattering in the presence of absorption. We filled two glass capillaries with a mixture of fluorescent quantum dots (SI Appendix, Fig. S1B) and submerged them in the phantom materials (SI Appendix, Fig. S1C). We chose quantum dots as the fluorescent probe in our study to obtain bright emission across all SWIR wavelengths. The quantum dots were excited with diffuse 808-nm light, and their fluorescence was imaged in 50-nm-wavelength bands across the SWIR (SI Appendix, Fig. S1D). We then quantified the contrast of each image using the coefficient of variation, which is defined as the ratio of the SD in signal intensities, σ, to the mean signal intensity, μ,

$$c_V=\frac{\sigma }{\mu }.$$ [1]

We find that only in the presence of absorption does contrast significantly change as a function of wavelength in the SWIR (Fig. 1 B and C). In the D₂O-based phantom, contrast increased slightly with increasing SWIR wavelength. In the H₂O-based phantom, on the other hand, contrast was overall greater, and increased considerably up to 1,450 nm before decreasing to the edge of our detection range at 1,600 nm. This behavior beyond 1,450 nm in particular reveals the important role of absorption in the enhancement of contrast, as the decline in scattering beyond these wavelengths should, in its absence, favor a contrast increase. We observed similar behavior in a relatively weakly scattering tissue phantom based on silica beads (SI Appendix, Fig. S3).

Fig. 1.

Water absorption enhances contrast in a tissue phantom through background signal suppression. (A) Attenuation spectra of the tissue phantom materials show scattering of light for 1% Intralipid in deuterium oxide (D₂O, orange line) and both scattering and absorption of light for 1% Intralipid in water (H₂O, blue line). (B) Images of capillaries filled with a mixture of SWIR-emitting PbS quantum dots in both D₂O-based (Top) and H₂O-based (Bottom) phantoms were taken, filtering the emission through 50-nm-bandwidth band-pass filters centered across SWIR wavelengths (complete set of images shown in SI Appendix, Fig. S1D). Integration times for all images are listed in SI Appendix, Table S1. All images are scaled to fill the maximum displayable intensities. (Scale bars, 1 mm.) (C) Contrast of the capillary images, calculated using Eq. 1, varies strongly with wavelength in the H₂O-based phantom and is overall greater than in the D₂O-based phantom.

We attribute the increase in contrast observed at wavelengths of strong water absorption, in part, to the suppression of background signal from the deeper submerged capillary. According to the Beer−Lambert law, signal attenuation depends exponentially on the depth of an emitting structure and the absorption strength of the medium. By varying the absorption strength, which we achieve by tuning the imaging wavelength, we can tune the depth at which signal falls below the noise level of the system, and thus control the relative intensities of structures at different depths. By imaging at wavelengths of strong absorption, we therefore preferentially suppress the signal from deeper objects in the background over the more superficial object of interest, improving the object contrast.

In addition, we find that water absorption also improves SWIR contrast by suppressing scattered light from the emitting object itself. We immersed a single capillary into the tissue phantoms and imaged with the same set of 50-nm band-pass filters (SI Appendix, Fig. S2A). Analyzing the intensity profile of the capillary cross-section reveals a narrowing of the intensity profile for wavelengths with strong water absorption (SI Appendix, Fig. S2B). Narrowing is also observed in the D₂O phantom, but to a lesser extent, particularly at 1,450 nm (SI Appendix, Fig. S2C). We quantified this effect by calculating the inverse of the capillary intensity profile peak widths at 10% maximum height and find that the metric is indeed the greatest at 1,450 nm, with broadening of the width observed for wavelengths longer than 1,450 nm (SI Appendix, Fig. S2D). This demonstrates that water absorption improves capillary image contrast and resolution by suppressing the detection of any scattered light, which has a high probability of being absorbed before reaching the detector. The relative trajectory lengths of scattered versus ballistic photons in scattering media such as tissue can be modeled using diffusion theory and/or Monte Carlo methods, as has been previously described and shown for visible wavelengths using an exogenous absorbing agent to suppress scattered photons (35–37). We discuss the theoretical trajectory lengths for our experiment in SI Appendix, Fig. S4.

Overall, our results suggest that water absorption is the primary inherent optical property which enhances fluorescence contrast across SWIR wavelengths. Given that our system is not diffraction-limited, we expect that highly scattered photons from deeper-lying structures, as well as scattered photons from an emitting object itself, are more likely to be absorbed than ballistic photons of the same object, as scattered photons travel a longer path length through the tissue before reaching the detector. This difference in absorption probability becomes more pronounced for wavelengths that exhibit stronger water absorption. As a result, fluorescence contrast is greatest at those wavelengths with the highest absorption.

Wavelength Dependence of Contrast in Vivo.

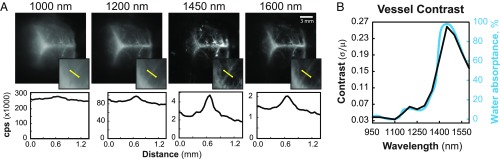
To investigate the wavelength dependence of contrast in vivo, we labeled the brain vasculature of a mouse using a mixture of quantum dots, and imaged the fluorescence through the mouse’s intact skin and skull in 50-nm-wavelength bands centered across SWIR wavelengths (Fig. 2A and SI Appendix, Fig. S5). The contrast $c_V$ (Eq. 1) was evaluated for each image, taken with a separate band-pass filter, and plotted as a function of band-pass center wavelength (Fig. 2B). In accordance with our phantom studies, we find that the wavelength dependence of contrast for the in vivo vasculature follows the same trend as the water absorptance spectrum, suggesting that water absorption also plays a key role in improving in vivo fluorescence image contrast at SWIR wavelengths. The contrast generally increases with wavelength until reaching a peak at 1,450 nm, then decreases beyond 1,450 nm, again supporting the dominant influence of water absorption on contrast over scattering, as the continuous decrease of scattering should cause an increase in contrast beyond these wavelengths. We verified our findings with additional contrast metrics (the signal to background ratio, the contrast to noise ratio, and the Weber fraction) and observed the same contrast trend for regions of interest over multiple different vessels, and for the entire brain image (SI Appendix, Fig. S6).

Fig. 2.

Correlation of in vivo fluorescence contrast with water absorptance. Brain vasculature of a mouse was fluorescently labeled with a broadly emitting InAs-based quantum dot mixture and imaged through ∼1 mm to 2 mm of intact skin and skull (12) with 50-nm-bandwidth band-pass filters centered in 50 nm spacing between 950 nm and 1,600 nm (SI Appendix, Fig. S5). (A) We show here images taken with 1,000-, 1,200-, 1,450-, and 1,600-nm filters and their respective intensity profiles in counts per second (cps) across a line of interest (yellow line in Insets) used to calculate the contrast (Eq. 1) of a vessel. Images are scaled to fill the maximum number of displayable intensities. (B) The contrast (black line) of the vessel plotted against band-pass center wavelength mimics the water absorptance spectrum (blue line).

Contrast and Penetration Depth Enhancement in ex Vivo Tissue Microscopy.

Conventionally, wavelengths of high tissue absorption have been avoided in fluorescence imaging, due to the belief that penetration depth is limited by photon collection. Indeed, if tissue attenuation is too high relative to the fluorescence intensity of the probe, emission from labeled structures will never reach the detector or will be indistinguishable from noise. However, we demonstrate here an example of a contrast-limited ex vivo tissue sample in which fluorescence image contrast and imaging penetration depth are both improved by imaging at SWIR wavelengths with strong tissue absorption.

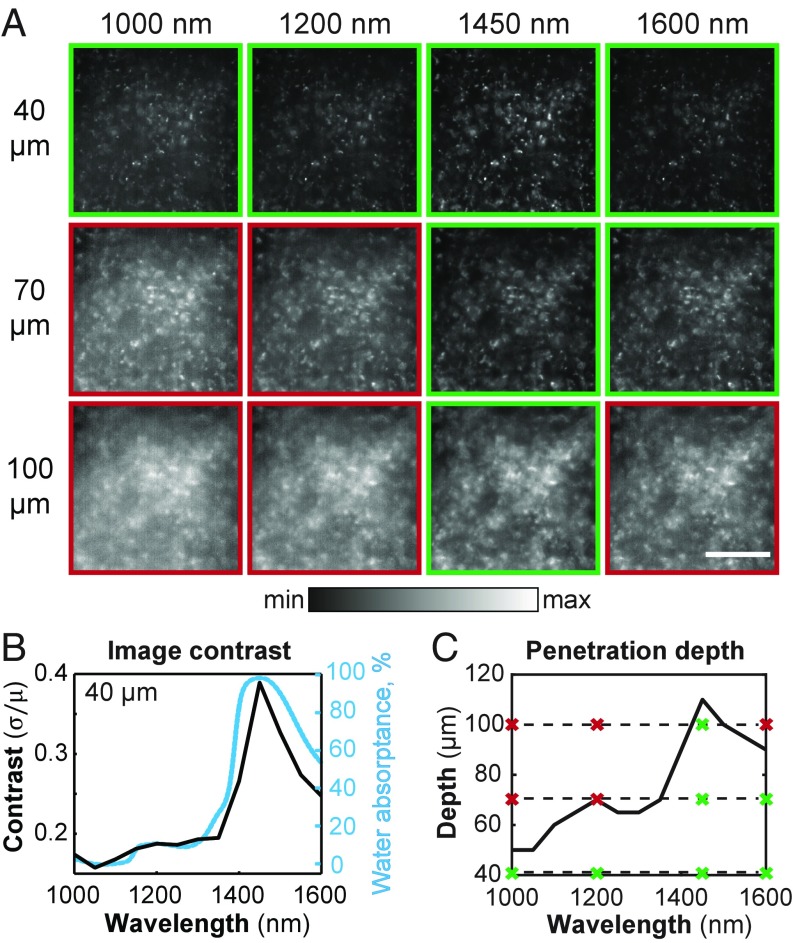
We labeled the Kupffer cells (tissue-resident macrophages) of a mouse liver using a broadly emitting quantum dot emulsion (SI Appendix, Fig. S7). We then acquired z stacks of the extracted, labeled tissue, filtering the emission through 50-nm band-pass filters centered across SWIR wavelengths (Fig. 3A). We determined the contrast, $c_V$ (Eq. 1), over the entire image for each wavelength (Fig. 3B). The penetration depth of the z stacks was then determined using an image processing algorithm adapted from Rowlands et al. (38) that determines the deepest tissue position at which an image with a given spatial resolution can be formed (Fig. 3C; see SI Appendix for algorithm details). Of note, the imaging performed in this study is not at the diffraction limit, and resolution—defined here as the minimum distance between two distinguishable features in an image—is primarily limited by contrast.

Fig. 3.

Contrast and penetration depth enhancement in microscopy of ex vivo liver tissue. (A) We labeled the Kupffer cells of a mouse liver using a broadly emitting quantum dot emulsion, and imaged the cells via microscopy with 50-nm band-pass emission filters centered across SWIR wavelengths, a subset of which are shown here at imaging depths of 40, 70, and 100 μm for 1,000-, 1,200-, 1,450-, and 1,600-nm filters. Integration times for all images are listed in SI Appendix, Table S1. All images are set to fill the maximum displayable intensities. (Scale bar, 200 μm.) (B) The contrast, $c_V$ (Eq. 1), was calculated and plotted as a function of wavelength (black line) for images taken at a depth of 40 μm. The contrast shows a similar trend to the water absorptance spectrum (blue line). (C) Furthermore, penetration depth was calculated using an algorithm adapted from Rowlands et al. (38) and plotted as a function of wavelength, showing a similar trend. The dashed lines mark the depths at which the images in A were taken, and the crosses display the wavelength positions. Green boxes and crosses indicate images considered to be resolvable within the contrast threshold.

Consistent with our macroscopic tissue phantom and in vivo data, we find that the liver microscopy images have the greatest contrast at wavelengths of high water absorption. Furthermore, we observe that the penetration depth likewise increases with water absorption. At shallow depths, e.g., 40 μm, an image of the labeled liver features is formed at all SWIR wavelengths, but imaging much deeper, e.g., 100 μm, causes significant loss of image contrast for most SWIR wavelengths except for those immediately around the water absorption peak at 1,450 nm. While, indeed, signal decreases when imaging at 1,450 nm versus 1,000 nm due to an almost 20 times greater optical density of the tissue, contrast and penetration depth more than double. Our data also demonstrate that, in this application, imaging at maximum absorption at around 1,450 nm enhances the penetration depth by almost 50% compared with imaging at 1,600 nm, which was previously believed to be the optimum for SWIR imaging (31). This observation shows that the contrast, and not the signal, limits penetration depth in this case. Although deep structures have sufficient signal to be detected, they are unable to be resolved, due to overlapping signal from structures in the background, foreground, or scattered light from the object itself. Imaging at wavelengths of strong tissue absorption enhances image contrast, and therefore enables resolution of deeper structures (SI Appendix, Fig. S8), resulting in a higher penetration depth.

Attenuation Dependence of Contrast and Penetration Depth in a Theoretical Contrast Model.

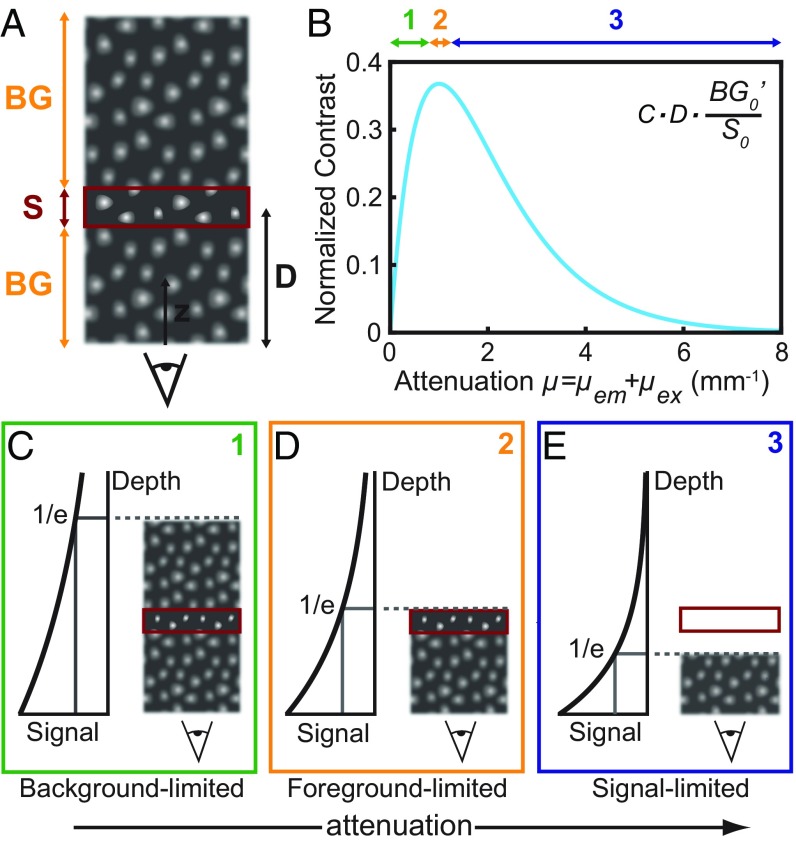
Given that it may be counterintuitive that tissue absorption can improve imaging penetration depth, we developed an illustrative theoretical model and show the existence of two regimes—one in which penetration depth is signal-limited, because not enough photons reach the detector, and one in which penetration depth is contrast-limited. In our model, tissue is described by a semiinfinite slab with emitting cells homogenously distributed throughout the slab, resembling the labeled liver tissue in our ex vivo tissue microscopy experiment. A signal of interest, S, arises from the focal plane at depth $D$, and a background signal, BG, arises from all planes elsewhere, i.e., above and below D (Fig. 4A). The background signal BG can result from, for example, autofluorescence, scattered photons from the signal layer, or fluorescence from nonspecific and/or out-of-focus labeled structures lying above or below D. In the case of our ex vivo tissue experiment, BG arose from both labeled cells outside of the focal plane and nonballistic photons scattered from their original source.

Fig. 4.

Theoretical contrast model shows contrast dependence on attenuation. (A) Schematic of the type of tissue modeled by our contrast model shows a semiinfinite slab of tissue containing homogeneously fluorescing cells. The signal (S) arises from the focal plane (red rectangle) at a given depth (D), and the background (BG) comprises emission from all other depths in the tissue. (B) The contrast was calculated for a fixed depth of 1 mm, varying the magnitude of the attenuation coefficient, which is a sum of the excitation wavelength attenuation coefficient μ_ex and the emission wavelength attenuation coefficient μ_em. (C–E) Schemes 1, 2, and 3 illustrate the relationship between contrast and attenuation coefficient as it relates to the emission from above and below the focal plane.

We first quantified the relationship between contrast and attenuation. We approximated the contrast as the ratio of signal intensity to background intensity, modeled according to Beer−Lambert’s law,

$$C=\frac{S_0}{B{G}_0^{\prime }}\cdot e^{-D({\mu }_{ex}+{\mu }_{em})}\cdot ({\mu }_{ex}+{\mu }_{em}),$$ [2]

where $S_0$ describes the in-focus signal intensity at zero depth, $B{G}_0\prime$ is the out-of-focus background intensity per millimeter slab at zero depth, and ${\mu }_{ex}$ and ${\mu }_{em}$ are the tissue-specific attenuation coefficients of the excitation and emission wavelengths, respectively, which consider all modes of attenuation (e.g., both absorption and scattering) (see SI Appendix for details). We note that this simple model cannot discriminate between ballistic photon and scattered photon positions, as is better described by diffusion theory and/or Monte Carlo methods (39–43). Rather, we weight S₀ greater than $B{G}_0\prime$ to roughly approximate the effect of the objective transfer function, and scattered photons are assumed to be homogenously distributed throughout the tissue (and thus averaged into the S₀ and $B{G}_0\prime$ terms). The model is sufficient to describe the results of our ex vivo tissue experiment in which cells are densely and homogenously distributed throughout the tissue, causing a relatively uniform background of scattered photons.

We plotted the contrast as a function of the total attenuation at a fixed depth of 1 mm. Our results show that, initially, contrast increases with attenuation, until reaching a maximum, after which stronger attenuation reduces the contrast (Fig. 4B). For a fixed excitation wavelength, this trend can be explained by the roles of the emission originating from behind the focal plane and the emission originating from in front of the focal plane. Initially, the stronger the attenuation, the less emission originates from background signal behind the focal plane, reducing background signal and increasing contrast (Fig. 4C). A maximum is reached when the attenuation length (namely the inverse of the overall attenuation coefficient) equals the imaging depth (Fig. 4D). If the attenuation is further increased, the signal from the focal plane is attenuated, and therefore the contrast decreases (Fig. 4E).

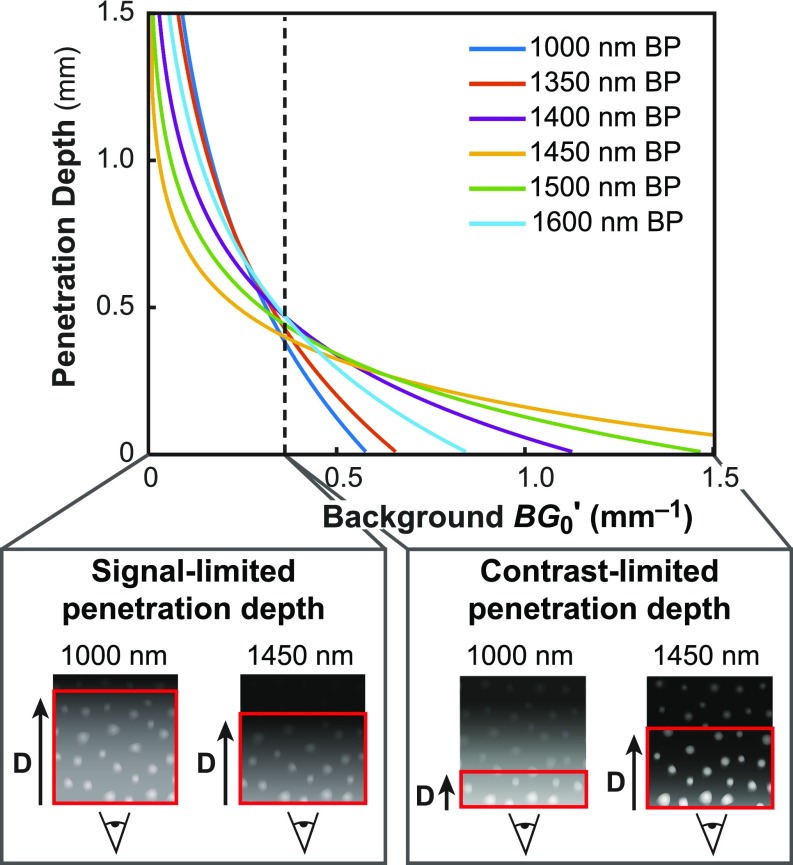
With this model, we further estimated the penetration depth trend across SWIR wavelengths. The penetration depth can be thought of as the maximum imaging depth at which one can still resolve the structures of interest; this depth is reached when the image contrast drops below some threshold contrast value. We calculated contrast as a function of imaging depth and as a function of inherent background signal (SI Appendix, Fig. S9A). Then, setting a threshold for the minimum resolvable contrast, we extracted the penetration depth for each wavelength (Fig. 5 and SI Appendix, Fig. S9 B and C).

Fig. 5.

Theoretical model of imaging penetration depth versus inherent background signal. By selecting a threshold contrast in our model to define the level at which structures are minimally resolvable (SI Appendix, Fig. S9), we extracted the effective imaging penetration depth for each wavelength, plotted here against background signal for select wavelengths. We find that, for a fixed signal intensity at small $B{G}_0\prime$, wavelengths of minimal absorption have the greatest imaging penetration depth, defining a signal-limited regime, whereas, at large $B{G}_0\prime$ wavelengths of strong absorption achieve the highest imaging penetration depth, defining a contrast-limited regime.

The results show the existence of two regimes which have opposite relationships between penetration depth and imaging wavelength. In the first regime, wavelengths with low tissue absorption favor contrast and therefore also penetration depth. This “signal-limited” regime, applies in the case when S₀/$B{G}_0\prime$ is inherently high, and large imaging depths are feasible, e.g., for systems with inherently strong contrast, such as tissue with a large, isolated emitting structure of strong signal or tissue with sparse label density and low background signal. In the second regime, wavelengths with high absorption enable the greatest contrast and simultaneously enable the greatest imaging penetration depth. The system is thus “contrast-limited,” which occurs in the case when S₀/$B{G}_0\prime$ is small, as in a highly labeled tissue with significant background emission, or for small, weakly emitting objects with inherently low signal to background ratios. We note that, while our discussion above centered on a fixed excitation and a varying emission wavelength, Eq. 2 implies that the same findings apply to the case in which excitation wavelength is varied while keeping the emission window fixed.

Discussion and Conclusions

Our findings provide a mechanism for tuning image contrast in biological SWIR fluorescence imaging using the inherent optical properties of the tissue. In a 3D tissue phantom, in in vivo brain vasculature imaging of a mouse, and in ex vivo microscopy of liver cells, we show that image contrast has a wavelength dependence governed by the absorption of the tissue, which is dominated by water absorption in the SWIR. We observe, in these experiments, that image contrast increases with increasing water absorption, and that contrast is the greatest at around 1,450 nm where absorption from water is the greatest. The idea that absorption can aid image contrast in a scattering medium (e.g., tissue) has been previously demonstrated; the underlying principle is that absorption preferentially suppresses photons having a longer path length through tissue (e.g., multiply scattered photons and fluorescence from deep background structures) which contribute to noise, over ballistic photons which form the image (35–37, 44). These prior studies administered exogenous agents to the sample to improve image contrast in the visible and NIR, whereas we show that the inherent optical properties of tissue in the SWIR provide sufficient variation in absorption to significantly affect image contrast without the need for an exogenous agent.

We show that fluorescence imaging contrast can be fine-tuned along the water absorption spectrum, but suppression of scattered light through absorption comes at the cost of decreasing the overall signal intensity, requiring longer integration times to achieve a sufficient signal to noise ratio. In our study, the bright indium arsenide- and lead sulfide-based quantum dots (13) used for contrast provided sufficient signal to be imaged in 50-nm-wavelength bands across the SWIR, eliminating signal limitations. However, for contrast agents that radiate less fluorescence signal and/or in the case of lower excitation fluxes, contrast may be limited by low signal levels relative to other sources of background noise (e.g., camera read noise or dark counts). In these cases, it may be necessary to choose an imaging wavelength that balances signal requirements with optimal scattering suppression, such as wavelengths near 1,300 nm to 1,350 nm or using a 1,300-nm long-pass filter on an InGaAs camera (SI Appendix, Fig. S10) (12, 18).

We have further demonstrated, in ex vivo liver tissue microscopy, and explained, with an illustrative theoretical model, that imaging penetration depth can likewise be tunable by selection of the SWIR wavelength (either the emission and/or the excitation wavelength). In our study, we achieved the greatest penetration depth at wavelengths of greatest water absorption, around 1,450 nm, which had the greatest image contrast. We describe this scenario as having contrast-limited penetration depth, and expect other tissues such as those with a high fluorescent label density, referring to tissue that contains many fluorescently labeled structures, strong autofluorescence, or other strong background signal, to show a similar effect. However, our theoretical model suggests that the penetration depth for other applications, such as those with low fluorescent labeling density, low background signal, or large, easily resolvable structures (e.g., whole organs), may be limited by signal rather than contrast. For these applications, wavelengths with lower absorption lead to the highest penetration depths. Furthermore, we expect that imaging with higher numerical aperture, and consequently a smaller depth of field, as in microscopy, will benefit more from this absorption effect than imaging with lower numerical aperture. We conclude that it is therefore important to understand whether a given imaging application is contrast-limited or signal-limited, to predict the behavior of the penetration depth with wavelength.

These results suggest an approach for improving both fluorescence image contrast and penetration depth in tissue by deliberate selection of specific SWIR wavelengths. The variation in the magnitude of water absorption within the SWIR spectral window distinguishes this wavelength region from the NIR, which was previously proposed as an ideal optical window for fluorescence imaging. Given these results, which show that contrast and penetration depth increase with increasing tissue attenuation, the SWIR wavelength regime may be preferable for imaging over the NIR in contrast-limited applications (e.g., resolution of fine, highly labeled structures, as in angiography). This work then further motivates the continued development of bright and biocompatible fluorescent probes for imaging at the longest and most highly absorbed SWIR wavelengths.

Materials and Methods

All animal experiments were conducted in accordance with approved institutional protocols of the Massachusetts Institute of Technology Committee on Animal Care. Detailed methods on the following subjects are available in SI Appendix: fluorescence imaging setup, tissue phantoms, quantum dot synthesis methods and characterization, capillary and in vivo brain vasculature images, contrast metric discussion, theoretical contrast model and penetration depth algorithm details, animal procedures, and tissue preparation details.