FEBio: History and Advances

Abstract

The principal goal of the FEBio project is to provide an advanced finite element tool for the biomechanics and biophysics communities that allows researchers to model mechanics, transport, and electrokinetic phenomena for biological systems accurately and efficiently. In addition, since FEBio is geared towards the research community, the code is designed such that new features can be added easily, thus making it an ideal tool for testing novel computational methods. Finally, since the success of a code is determined by its user base, an integral part of the FEBio project has been to offer support and outreach to our community, to provide mechanisms for dissemination of results, models, and data, and to encourage interaction between users. This review article presents the history of the FEBio project, starting from its initial developments through its current funding period. A glimpse into the future of FEBio is presented as well.

1. INTRODUCTION

The finite element (FE) method has proven to be one the most versatile numerical methods for solving computational problems in physics. Although it was initially applied to problems in mechanics, it has since its inception in the 1950s been used in virtually every field of engineering and physics, including solid mechanics, fluid flow, heat transfer, electromagnetism, diffusion, and many more. In the field of biomechanics the FE method was applied to problems as early as the 1970s (e.g (1–6)). Since that time, the application of FE analysis in biomechanics research and design has increased exponentially as commercial software and improved computing platforms made the method more accessible to the research communities. Applications have spanned from the molecular level to cellular, tissue and organ levels.

The field of biomechanics has made tremendous advances over the last few decades as our understanding of the complex structure of biological tissues has grown. As an example, the development of mixture theory as an accurate approach for modeling the interaction of the solid and fluid components of living tissues has resulted in many new insights (7–13). However, the lack of FE software that is tailored to the needs of the field has hampered research progress, dissemination of research, and sharing of models and results. The commercial packages that are most commonly used by the biomechanics community are not specifically geared towards biological applications. In addition, the closed nature of commercial codes makes them difficult to verify (14; 15) or to compare results across different codes since the implementation details are often unavailable. Commercial codes often do not offer a mechanism for adding new features easily. This makes it challenging for researchers to implement and test new computational methods or constitutive models.

The limitations of commercial codes forced many researchers to develop custom FE packages for solving problems in the biomechanics domain. One of the earliest examples of a finite element code developed for applications in biomechanics was by Simon et al. (16), who developed a custom code for modeling intervertebral disc segments based on porous media theories. FE implementations of biphasic theory for cartilage were presented by Spilker and coworkers, for small strains (17) and finite deformation of the solid matrix (18), using penalty methods to enforce incompressibility. They considered various refinements to their approach (19), including hybrid, mixed-penalty and velocity-pressure formulations (20; 21) as well as tissue anisotropy (22) and explicit modeling of interstitial fluid viscosity (23). u-p (displacement-pressure) formulations of the biphasic mixture theory were presented by Oomens et al. (13) and Wayne et al. (24), and a biphasic formulation accommodating solid matrix viscoelasticity was developed by Ehlers et al. (25). Custom-written FE codes for modeling deformation, electrokinetics, transport and swelling of charged hydrated tissues were developed by Simon et al. (26; 27), Levenston et al. (28), Sun et al. (29), and Frijns et al. (30). Although these custom-written codes implemented more advanced modeling and solution algorithms than were available in commercial packages, few of these codes were actually made available in the public domain. This made verification and reproducibility of results challenging or impossible. Many of these codes were also not sufficiently general, but instead designed for solving very specific problems and did not support all features that are necessary for analyses in computational biomechanics and biophysics. In addition, to the best of our knowledge, at the time development of FEBio started (c. 2005) none of these custom-written codes offered extended documentation, support, or mechanisms for continued development.

Due to the many limitations of commercial and custom-written FE packages, the authors (and many others in the research communities) felt there was a genuine need for a new FE tool: a tool that would be designed by and for the biomechanics community. FEBio was developed to fill this need. In order to accomplish its goals, it would be designed around three pillars. First, it would specifically target the biomechanics community by focusing on features that are relevant in the field. This would include, for example, accurate constitutive relations for mechanical, transport, and electrokinetic properties of tissues and cells; the ability to easily model anisotropy and inhomogeneity; and the ability to prescribe boundary conditions and loading scenarios that would allow researchers to model the complex interactions between biological structures. Second, the source code would be freely available and designed such that it would be easy for researchers to implement new algorithms (e.g. new constitutive models). This would greatly reduce the need for new custom-written codes and overcome the problems with verification and repeatability of results as researchers can easily share their new additions and algorithms. Third, emphasis would be placed on thorough documentation, support, and outreach to the community, which would make it much easier than before for researchers to develop new ideas and share them with others.

2. INITIAL DEVELOPMENT (2005–2009)

2.1. The FE Kernel

In 1995 Weiss was involved in the development of a deformable image registration algorithm termed Hyperelastic Warping (31). This method uses a finite element method for solving the image registration problem. The result of this approach is a deformation that is physically realistic and can be used to calculate the strains and, assuming the constitutive properties of the materials are known, the stresses as well. This algorithm was originally implemented in NIKE3D, a nonlinear implicit finite element code for solving problems in solid mechanics, developed by the Lawrence Livermore National Laboratories (LLNL). Weiss obtained the source code for NIKE3D through their LLNL licensing mechanism and used the code for solving problems in computational biomechanics (32–34). A special version of NIKE3D was developed that included the Hyperelastic Warping algorithm. Unfortunately, NIKE3D was not free and, as a government-owned program, the dissemination of the additions was complicated. Consequently, the algorithm was not widely used outside Weiss’s lab despite the fact that it had many valuable applications (35–37) (Figure 1). To overcome this problem, the idea started to develop a new, custom, open-source, FE kernel that would serve as the engine that drives the future developments of the warping algorithm.

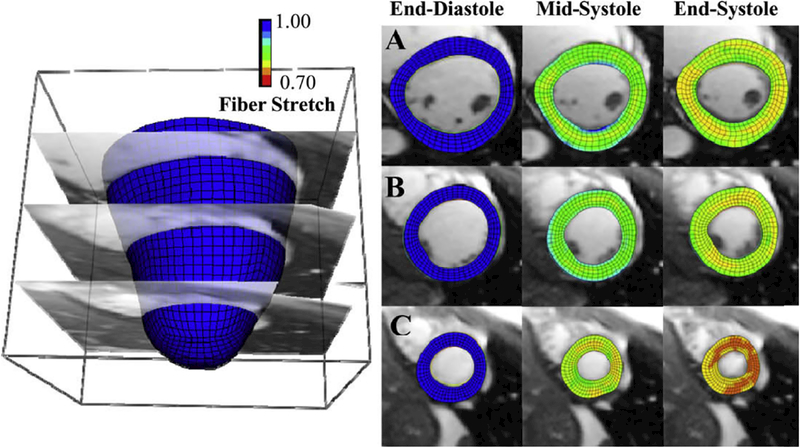
Figure 1:

Example of an application of the hyperelastic warping method which combines a finite element kernel with an image registration technique. LV fiber stretch developed through systole (left column – end-diastole, fiber stretch = 1.0, middle – mid-systole, right – end-systole) with the Hyperelastic Warping solution depicted at (A) basal (B) mid-cavity and (C) apical slices.

The development of this FE kernel commenced in 2005 at the same time that Maas joined Weiss’s lab. However, it was quickly realized that the kernel could be used for solving traditional finite element problems as well, and in fact could replace the dependency on NIKE3D. This became a pressing concern at the time because LLNL reported it would soon discontinue development of NIKE3D. This kernel code was greatly expanded in 2005 and 2006 and became the predecessor to FEBio. When other researchers started to express interest in our new code, the idea of FEBio was born: a new finite element code specifically designed for the biomechanics community. Ateshian, who had previously collaborated with Spilker et al. (38) and later developed his own custom finite element codes for analyzing contact of biphasic cartilage layers (39; 40), became one of the earliest researchers to express interest in the FEBio project. With his expertise in mixture theory, Ateshian joined forces with Weiss and started working on the incorporation of biphasic modeling capabilities in FEBio, a capability that was of significant interest to the biomechanics community.

The main focus of the first version of FEBio was the implementation of a nonlinear, implicit finite element solver for large deformation mechanics. The formulation was based on the discretization and linearization of the virtual work equation (41) and the implementation of robust quasi-Newton methods for solving the non-linear FE equations (42). Constitutive models were mostly defined using hyperelastic strain energy density functions. Nearly-incompressible materials were implemented using uncoupled formulations and a three-field variational formulation to overcome locking issues (43). Transverse isotropy was also supported in some of the material models (44) as well as viscoelasticity (45). The implementation of viscoelasticity allowed any of the hyperelastic materials to be used as the elastic component. A special material type was defined for rigid materials, which implicitly defined the rigid parts of the model. Rigid bodies were modeled using an efficient method based on the reduction of degrees of freedom (46). Frictionless sliding and tied contact algorithms were also implemented using an augmented Lagrangian approach (47), although a standard penalty formulation was available as well. A biphasic material was also supported, which required the specification of the elastic mixture response material and the permeability of the solid phase. When such a material was defined, FEBio would essentially solve a coupled displacement-fluid pressure problem where the virtual work equation combines the mixture momentum and mass balance equations using a monolithic approach (40).

2.2. PreView and PostView

FEBio was developed as a command-line tool. This choice was mostly motivated by our initial intent to continue using our available pre- and post-processing software and focus our efforts solely on the development of the FE solver. Thus, FEBio would take an input file, solve the problem, and return the results in one or more output files. We took advantage of our experience with NIKE3D and initially used the same input and output file formats. This allowed us to continue using the commercial code TrueGrid (truegrid.com) to generate the input file and LSDYNA PrePost (lstc.com) for post-processing. Of course, this presented a problem for other users of our code since they would be required to purchase TrueGrid and LSDYNA in order to use FEBio. We reasoned that it did not make sense to offer a free software package that required a significant financial investment in order to use it, motivating us to develop our own pre- and post-processing software.

Another limitation was that these initial file formats were static. The structure and contents of the files were predefined and could not be changed easily. Since one of the aims of the FEBio project was to allow researchers to add new features, this limitation would severely complicate the process of adding new input data and storing new output data fields. Therefore, a new, extendable input (the “feb” format) and output format (the “xplt” format) were designed. Being able to support these new formats was another motivation for the development of custom pre- and post-processing software.

The FE pre-processor was termed PreView and initially allowed the import of volume meshes and the definition of boundary conditions, material and analysis parameters. Users would then export the model definition as a FEBio input file. This initial implementation still posed the problem of how to generate the FE meshes. However, at that time, it was felt that many software packages were available, commercial as well as free, to achieve these tasks so this issue was not considered a severe limitation.

For post-processing and analyzing the FEBio results, PostView was developed. The initial implementation of PostView was actually an adaptation of another software package, called WarpLab, which Maas had developed for analyzing the results of the Hyperelastic Warping algorithm.

2.3. FEBio 1.0

The first version of FEBio was released in December 2007. It was developed using the C++ programming language. This was a break from tradition since many FE codes at the time were still being developed in FORTRAN. In fact, most of the authors’ initial experience with FE codes was in FORTRAN due to our work with NIKe3D, which was written in FORTRAN. However, at the time C++ had become an accepted language for scientific programming, mostly as a result of its maturation as a language and the availability of efficient compilers that made it competitive with FORTRAN (48). The largest advantage of C++ over FORTRAN was its support for object-oriented design, which greatly simplifies the development of large, complex software. This decision was vindicated after initial benchmark problems showed that FEBio outperformed NIKE3D quite well. Of course, this improved performance cannot be attributed solely to the chosen programming language, since NIKE3D was optimized for the now mostly obsolete vector-processing machines, whereas FEBio was designed to target more modern computer architectures. Nevertheless, the excellent initial performance of FEBio was encouraging.

As part of the first FEBio release, a forum was created where users could submit questions, report bugs or propose new features. The software was made available for download from the website of Weiss’s Musculoskeletal Research Laboratory (MRL) at the University of Utah. Both pre-build binaries and the source code itself were available for download.

3. FIRST FUNDING PERIOD (2008–2012)

3.1. Multiphasic Framework

In 2008 we received our first federally funded grant for the FEBio project through the U.S. National Institutes of Health. The main goal for this funding period was to expand FEBio’s capabilities for modeling problems in biomechanics. In particular, the initial implementation of biphasic (or poroelastic) materials was to be extended to mixtures with multiple constituents, using the general framework of mixture theory. This allowed the representation of mixtures consisting of a solid matrix, solvent, and initially only one (40), but later any number of solutes. A special emphasis was placed on solute-solid matrix interactions, including solute exclusion from a fraction of the matrix pore space (solubility) and frictional momentum exchange that produces solute hindrance and pumping under certain dynamic loading conditions (49). The finite element formulation implemented full coupling of mechanical and chemical effects, providing a framework where material properties and response functions may depend on solid matrix strain as well as solute concentration. The implementation was verified using canonical problems for which analytical or alternative numerical solutions exist. Additional boundary conditions were also implemented to accommodate the complete set of boundary conditions applicable to a solid-fluid mixture, including prescribed solid displacement, fluid pressure, total traction, effective traction, normal fluid flux, and fluid volumetric flow rate. A general theoretical framework for formulating constitutive relations for anisotropic, strain-dependent permeability and solute diffusivity in multiphasic mixtures was also developed, since some of the fundamental principles for such formulations were lacking in the prior literature (50).

Furthermore, to accommodate contact between solids and mixtures having a solid matrix, new contact algorithms were implemented that properly accounted for conservation of mass and momentum between contacting mixtures. These contact algorithms allowed both the solvent (Figure 2) and solutes (Figure 3) to flow across the contact interface (51; 52).

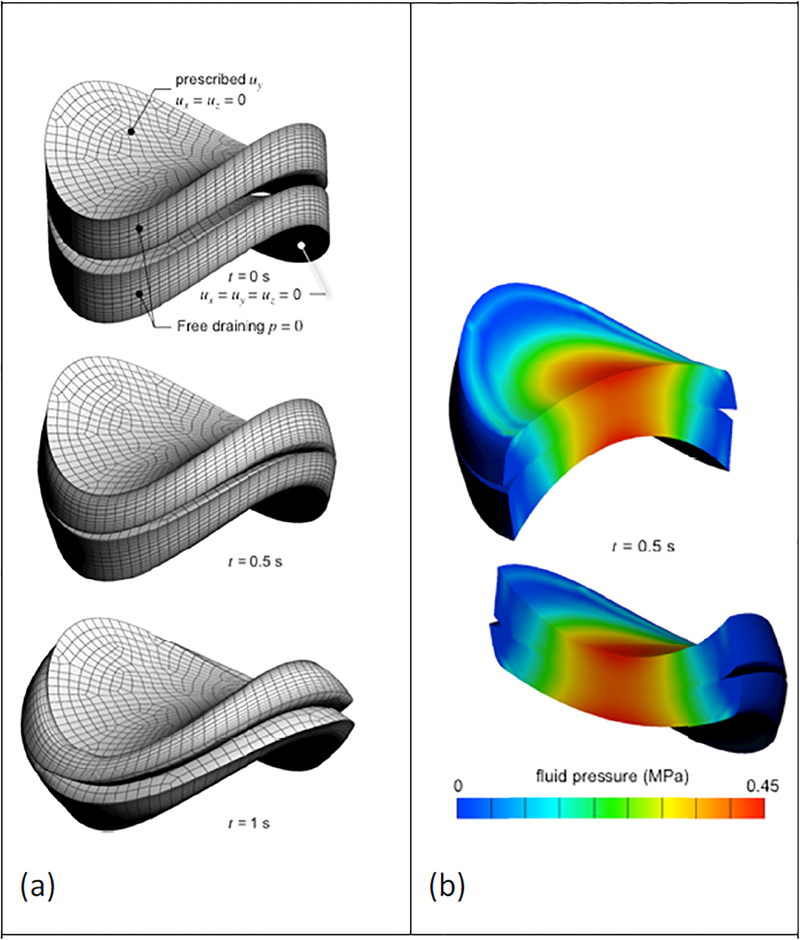
Figure 2:

Biphasic contact of saddle-shaped articular layers. (a) Boundary conditions and mesh deformation at various time points. (b) Fluid pressure distribution shown on cross-sections at t=0.5 s. Notice the continuity of the fluid pressure across the contact interface.

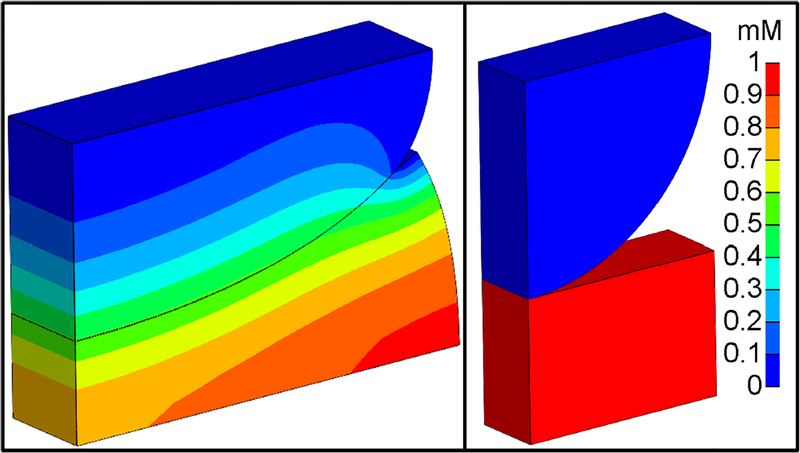
Figure 3:

Contact analysis with solute transport. Right: Initial configuration. The solute concentration is initially 1 mM in the bottom body and 0 mM in the top body. Left: During finite deformation contact, solute transports from the bottom body to the top body, enforcing concentration continuity at the contact interface.

A particularly useful feature of FEBio has been the ability to model mixtures of solid constituents, allowing users to combine various models available within the solid material library to produce custom materials with very little effort. This feature has been particularly useful for modeling fibrous tissues as mixtures of one or more fiber families that only sustain tension, superposed with a ground matrix that may also support compression. Without a ground matrix, such tension-only material models would otherwise be unstable (53). The ability to model biological tissues using continuous fiber distributions has also been added to FEBio, since these models have been shown to produce far better agreement between theory and experiments for some tissues (54). A special class of solid mixtures has been introduced, which allows the various solid constituents to have distinct reference configurations; this feature makes it possible to model multi-generational growth of biological tissues, including the evolution of residual stresses with evolving growth (55).

3.2. Enhanced Tetrahedral Elements

Another important goal of this funding period was the implementation of tetrahedral formulations that are suitable for large deformation mechanics, especially for modeling near-incompressible materials. As is well-known, linear tetrahedral formulations perform poorly under these conditions and have a tendency to lock, i.e. they grossly under-predict the displacements under applied loads (56). Yet, the use of linear tetrahedral elements is appealing in finite element modeling due to the ease with which complex geometries can be meshed with such elements. To overcome the limitations of linear tetrahedral elements, an enhanced tetrahedral element formulation (the UT4 element) was implemented in FEBio (57; 58). This formulation evaluates the finite element equations at the nodes as the average of the quantities evaluated at the adjacent elements. However, the nodally averaged results are inherently unstable, and therefore a weighted sum of the standard linear tetrahedral residual and the new nodally averaged one is used to improve stability. Unfortunately, despite obtaining some promising initial results for certain test problems, this element formulation ultimately demonstrated inaccurate results, especially for contact problems, and spurious deformation modes (59).

3.3. Pre- and Post-processor Enhancements

During this funding period, our existing pre- and post-processing software packages were also expanded. Support for tetrahedral mesh generation was added using TetGen (tetgen.berlio.de), which allowed users to convert triangulated surfaces (created, for instance, using image segmentation software) into tetrahedral finite element meshes. In addition, support for boundary conditions on multiphasic mixtures was also implemented, which allowed users to prescribe fluid pressures, fluid flux, solute concentration, solute flux, mixture normal traction as well as apply contact interfaces that take fluid and solute transfer between the contacting surfaces into account. Finally, support for defining biphasic, triphasic and multiphasic materials was added in PreView.

3.4. Validation and Verification

In order for any simulation software to gain credibility, it must be subjected to a well-defined verification and validation process. FEBio was verified by comparing its predictions to both analytical solutions as well as results obtained with other FE codes (60). In addition, a rigorous regression test suite was developed that ran nightly and ensured that FEBio produced consistent results. The test suite currently contains over 160 problems. The test suite was also made available to users so that they could ensure that FEBio worked properly on their computing platforms as well.

3.5. Expansion of Support Mechanisms

An integral part of the FEBio project was to provide mechanisms for user and developer support, as well as encouraging interactions between members of our community. The MRL web site (http://mrl.sci.utah.edu) was completely redone and launched in February 2010. Registered users could download FEBio, PreView and PostView executables for Windows, Mac and Linux operating systems. The source code for FEBio was also made available for download. Manuals were made available online for the first time, along with downloadable PDF files, and an updated help system with search capabilities was implemented. The online FEBio source code documentation was generated with Doxygen (www.doxygen.org).

4. SECOND FUNDING PERIOD (2012–2016)

4.1. Multiphasic Models and Chemical Reactions

During the second funding period, the multiphasic framework was expanded to include modeling of any number of neutral or charged solutes in a porous deformable solid matrix that may carry electrical charge (61). The inclusion of solutes and charged solid matrix made it possible to model osmotic effects that play a dominant role at the cellular level (62) and in a variety of soft tissues that exhibit a significant fixed charge density (63–65). Thus, it became possible to analyze Donnan osmotic pressure, electro-osmosis, electro-diffusion, and other eletrokinetic phenomena that are relevant to biological tissues. Chemical reactions were also incorporated into the code to allow mass exchanges between solutes and solid-bound molecular species. Any number of chemical reactions could be included in a particular multiphasic mixture material. Four standard constitutive relations were incorporated into the code, including the law of mass action for forward reactions, the law of mass action for reversible reactions, Michaelis-Menten kinetics as a special case of the law of mass action, and the solid remodeling theory of Huiskes and co-workers (66). The validity of the code was verified for a number of problems for which analytical solutions are available (67) (Figure 4). For example, these implementations made it possible to investigate the role of nutrient transport and consumption in tissue engineering studies (68; 69), and binding kinetics of growth factors to the scaffold, extracellular matrix and cells in a tissue construct (70).

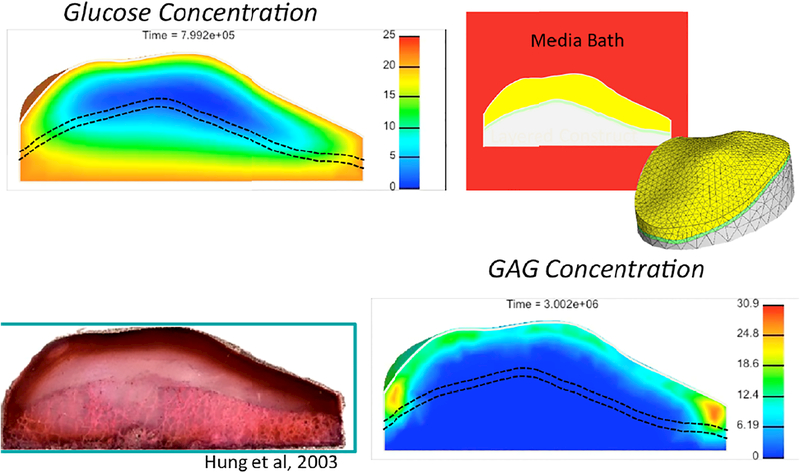
Figure 4:

A finite element model of a human patella-sized engineered tissue construct (mesh shown at center right) was analyzed using chemical reactions to model glucose consumption from the available media bath (top right), as well as glycosaminoglycan (GAG) synthesis in response to glucose availability. The glucose concentration at an intermediate time point during the growth process is shown in the top left panel, indicating limited glucose availability near the center of the construct due to consumption by cells at the construct periphery. The concentration of synthesized GAG at the final time point in simulated culture is shown in the bottom right panel, demonstrating that GAG synthesis occurred predominantly near the articular surface. The Safranin-O staining of a real tissue construct, cultured under the conditions simulated in the finite element model, is shown in the bottom left panel. Agreement between the model and experiment validates the modeling method.

Related to the expansion of the multiphasic framework, the implementation of body forces in biphasic materials was implemented, which served as a template for the implementation of active solute transport in the form of a solute momentum supply. Ongoing studies aim to demonstrate the application of this reactive framework to model active transport processes in cells, such as those involved in cell volume regulation, pH regulation, and Calcium signaling.

Our formulation of a reactive mixture framework for constrained solid mixtures also produced unexpected benefits, such as the ability to reproduce the classical theory of linear viscoelasticity using bond breaking and reforming reactions (rather than the classical springs and dashpots); with this novel approach to a classical problem, we were able to formulate more general theories of nonlinear viscoelasticity (71), which have now been implemented in FEBio. The same reactive constrained mixture framework has also allowed us to model damage mechanics in tissues, by modeling the permanent bond-breaking process as a reaction (72); this damage framework has also been implemented in FEBio, allowing users to implement damage in any of the existing solid materials, using a variety of damage criteria. We have applied this model to investigate damage mechanics in cartilage constructs that are subjected to excessive Donnan osmotic swelling due to a more rapid synthesis of charged proteoglycans than a restraining collagen matrix (72).

The FEBio framework has been designed such that users may combine any of these models as needed: For example, a multiphasic material may be set up with a charged solid matrix and multiple neutral or charged solutes; the solid matrix may be modeled as viscoelastic, or may be allowed to undergo damage in response to loading, at the same time that growth and degradation processes are taking place, driven by chemical reactions involving solutes and solid-bound molecules. Importantly, the material properties may also evolve with the evolving composition, so that tissue remodeling analyses may be easily accommodated.

4.2. Plugins

One of the important design goals for FEBio was to make it easy for users to expand the source code and add new features. The initial versions of FEBio used principles from object-oriented programming to create a modular structure of the code that could be modified easily. Although it was possible for users to download the source code and modify it directly, this process presented some practical limitations. A significant issue was that after the user modified the code, this customized version might not be compatible with the next FEBio upgrade, requiring significant effort to port changes to the new version. Another difficulty for developers was the need to build the entire FEBio source code tree from scratch, even if they only needed to make a small modification. Since FEBio depends on third-party libraries (e.g. MKL for PARDISO linear equation solver, levmar for optimization, zlib for data compression) – some of them not free – users would be required to obtain these third-party libraries as well. To overcome this limitation, a plugin framework was developed for FEBio that allowed users to create customized tools without the need for modifying or recompiling the FEBio source code. The plugins were implemented as stand-alone libraries (dynamically linked libraries on Windows, or shared object libraries on Linux and Mac) that are linked to the FEBio executable at run-time. Each plugin implements a new feature by extending the classes that are defined in the FECore library, which is a library that contains all the base classes that are used by FEBio. The plugins are compiled and built separately from the FEBio code. To link the plugin with FEBio, the user simply adds the path to the plugin in the FEBio configuration file and FEBio will automatically load the plugin at run-time and add the classes defined in the plugin to the FEBio framework. This plugin feature allows users to extend almost every part of FEBio, such as adding a new material model, customizing or extending the plot file output, coupling FEBio to other codes, and much more.

For example, a plugin was developed to couple FEBio to a computational model of angiogenesis (73). The coupling allowed us to include matrix deformations and study the effects thereof on the growth of the microvessel fragments (Figure 5). Another plugin has implemented Weiss’s original Hyperelastic Warping algorithm (31), which now makes use of FEBio as its FE kernel. This plugin adds image-based body forces that register a FE mesh onto a target image (Figure 1). A plugin was also developed for applying pre-strain to models (74). With this plugin users can apply an initial strain to the reference configuration (Figure 6), an important application for modeling biological tissues, or pre-stress a geometry by solving an inverse FE problem. These three examples illustrate the versatility of the plugin framework and demonstrate that it provides a powerful tool for extending the capabilities of FEBio.

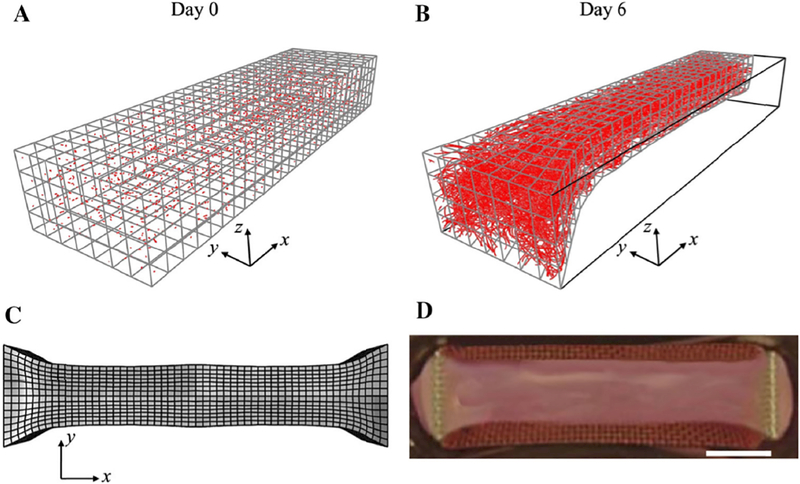
Figure 5:

Example illustrating the application of the FEBio angiogenesis plugin. Simulation of a long axis constrained (LAC) vascularized gel. A) At Day 0, the mesh was seeded with initial microvessel fragments. B) At Day 6, the gel was highly perfused by microvessels and has deformed into a ‘neck’ shape as seen in the LAC experiments. C) Full-geometry construction of the gel as predicted by the deformed FE mesh. D) The deformed gel geometry predicted in the simulation closely resembled the shape of long axis constrained vascularized gels at Day 6. (Scale bar 2 mm).

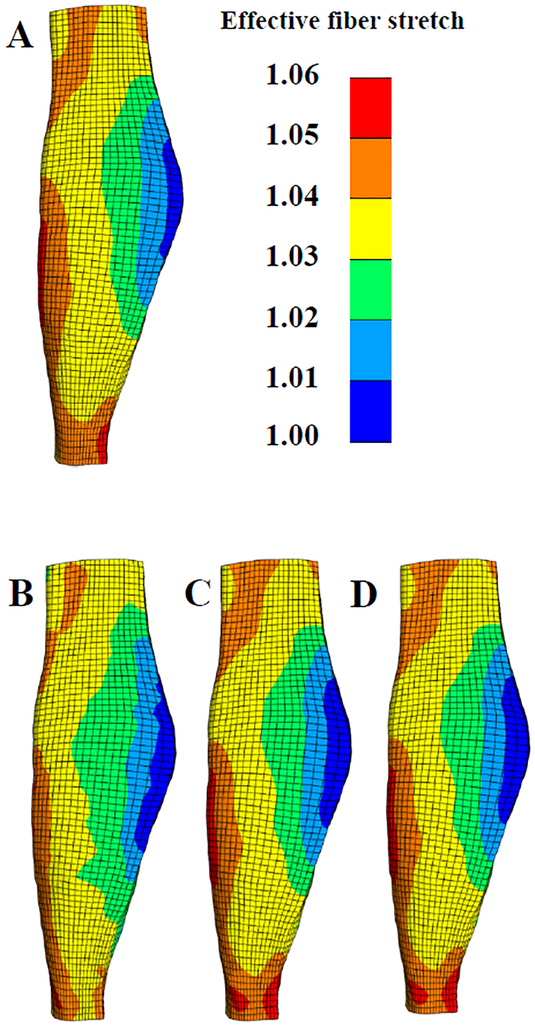
Figure 6:

Effects of applying in situ stretch to a reference geometry that is kinematically incompatible. (A) Reference geometry with target in situ fiber stretch. (B) Deformed state and effective fiber stretch without updates. (C) Effective fiber stretch after eliminating distortion. (D) Effective fiber stretch after enforcing the target in situ stretch.

4.3. Parallelization

Initially, FEBio did not take advantage of parallel architectures on desktop computers, at least not directly. Support for parallelization was a result of using third-party parallel linear solver libraries (e.g. Intel MKL PARDISO, software.intel.com/en-us/articles/intel-mkl-pardiso). The justification for this design choice was the fact that, as an implicit finite element solver, the factorization of the global stiffness matrix takes up most of the solution time. At the same time, the use of quasi-Newton methods (42), which do not require the factorization of the stiffness matrix at each iteration, meant that more time was spent in the serial part of the code. In addition, the development of more complex constitutive models (e.g. continuous fiber distribution materials (75)) significantly increased the time spent evaluating the stiffness matrix and right hand side vector. The result was that the serial part of the code had now become a significant bottleneck; to overcome this limitation the serial parts of the code had to be parallelized. OpenMP (openmp.org) was chosen as the parallelization mechanism as this was the easiest path to parallelizing a serial code. The parts of FEBio that were most time consuming were identified and, where possible, were rewritten with support for OpenMP. This included most stiffness matrix calculations and right-hand-side evaluations where the loop over all elements was parallelized. Some aspects of the contact projection algorithms, which turned out to be costly in terms of run time, were also parallelized. Some of the error handling routines also had to be rewritten since they were not thread-safe. This initial effort resulted in some encouraging benchmarks. The initial parallelization effort left the assembly of the global structures from the element structures as a critical section, so that this part of the solution process remained serial. This limitation was later removed and resulted in slightly better performance of the parallel code. Additional improvements were achieved by experimenting with different loop splitting mechanisms.

Although the parallel version of FEBio (starting with FEBio 2.0) greatly improved the performance for many problems, the overall performance gain was highly problem dependent and was affected by the time spent inside the linear solver. The most dramatic reductions in run time (up to a factor of 3.5 on architectures with 8 processors) were observed for problems that spend the most time outside of the linear solver, such as contact problems or problems that use complex constitutive models.

4.4. Quadratic Tetrahedral Elements

Since the UT4 elements did not prove as successful as initially anticipated, especially for contact problems, the search for efficient tetrahedral formulations continued. This time, the focus was on quadratic tetrahedral formulations. During this grant period several quadratic tetrahedral element formulations were implemented in FEBio. These elements are an attractive alternative to linear tetrahedral elements since they maintain the advantages of tetrahedral mesh generation. In addition, they can represent curved boundaries more accurately than linear elements since their edges and faces are curved, reducing the need for fine meshes for representing curved structures. In addition, as reported in a recent publication (76), it turns out that quadratic tetrahedral elements perform similarly and sometimes even better, both in terms of computational cost and in terms of accuracy, than the “gold standard” linear hexahedral element (Figure 7).

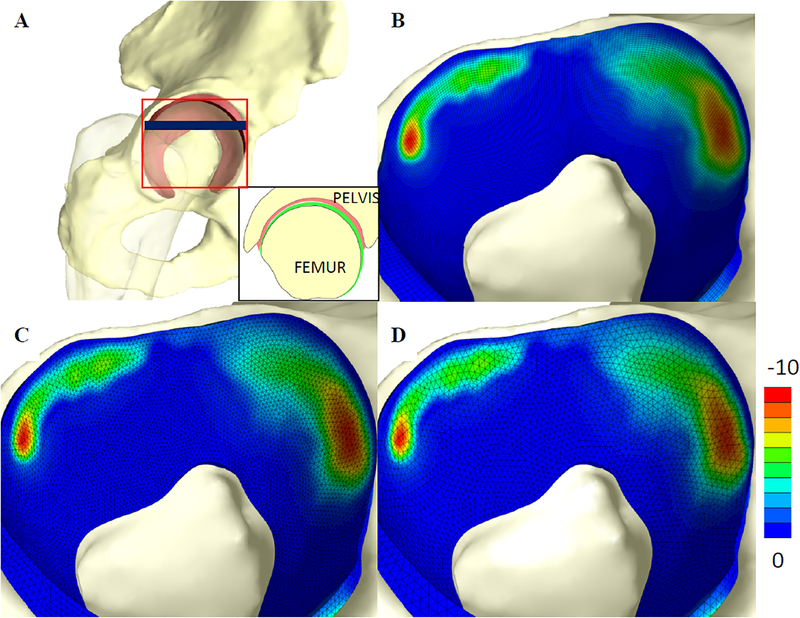
Figure 7:

A) Finite element model of the human hip, including the acetabulum, proximal femur and articular layers on the acetabulum and femoral head. Red square shows approximate area corresponding to contour plots. Blue line shows approximate location of inset, showing cross-section of model B-D) Fringe plots of 3rd principal stress for the acetabular cartilage discretized with B) HEX8 elements, C) TET10 elements, and D) TET15 elements. There was very good agreement between the 3rd principal stress and contact area predicted by the three models.

5. IMPACT OF FEBIO

5.1. Overall impact

To this day the FEBio user’s community continues to grow. Since the first release of FEBio in 2007, there have been over 110,000 software downloads. Currently, there are more than 5,100 registered FEBio users and around 1,100 registered users on the forums, and these numbers continue to grow. Our user base ranges from students, some of them new to finite element modeling, to more experienced academics and researchers. FEBio is also used as a teaching tool in various institutes across the world, such as the University of Michigan, Boise State University, Technical University of Madrid, National University of Singapore, University of Strathclyde, Brigham Young University, Eindhoven Technical University, Tel Aviv University, McGill University, and several others. FEBio has also been featured in many posters and podium presentations during various conferences over the years.

Although these statistics give a glimpse of the positive impact of FEBio on the community, perhaps the best way of estimating its impact is by looking at how the software has been used by other researchers. Currently, we are cognizant of at least 216 articles in peer reviewed publications that have used FEBio in a significant way, covering areas of soft tissue mechanics, tissue engineering, joint and muscle mechanics, damage modeling, cardiovascular mechanics, angiogenesis, modeling of vision and hearing, multiscale modeling, and many more. An exhaustive review of these articles is beyond the scope of this article (see febio.org for the full list). Instead, a few selected examples are presented below.

5.2. Specific Use Cases

Few commercial codes offer effective sliding contact algorithms under large deformations for poroelastic materials. ABAQUS (abaqus.com) has emerged as the de facto gold standard in biomechanics (77–86). It offers a contact algorithm that may be customized with user-specified routines to accommodate fluid pressure and fluid flux interface conditions compatible with biomechanics applications, such as articular joint contact (87). With the introduction of a biphasic contact algorithm in FEBio (51), at least two independent studies have been recently published in the biomechanics literature (83; 88), whose aims were to compare ABAQUS and FEBio. Both studies demonstrated favorable agreement for a variety of test problems, concluding that either code could be used effectively for such applications.

In (89) the authors implemented a new constitutive model of slightly compressible transversely isotropic material which overcomes some of the limitations of the traditional approach to implementing nearly-incompressible formulations. This material model was implemented in both ABAQUS (as a user subroutine) and FEBio (as a material plugin) and the performance of the codes were compared. Although the results between the codes agreed well, FEBio was notably faster. Due to FEBio’s tensor class and operator library, the implementation in FEBio was considerably easier. In addition, FEBio offers a diagnostic routine for checking the consistency between the stress and tangent implementations, which gives confidence that the implementation is correct. ABAQUS does not offer such capabilities, making the implementation of a new constitutive model much more difficult.

The OpenKnee project (90; 91) is a collaborative effort between several institutes and research labs and one of its main goals is the development of freely available finite element models of the human tibiofemoral joint. These models include detailed anatomically correct models of the femur and tibia, cartilage layers, medial and lateral menisci, and cruciate and collateral ligaments. The models are available for download as FEBio input files. The OpenKnee project showcases how new synergetic collaborations have been formed out of the FEBio project and how these new collaborations have driven the FEBio development. For example one of the outcomes of this collaboration was the development of a plugin that allows users to apply prestrain to finite element models, an important application for accurate modeling of biological tissues (Figure 8). The expansion of FEBio’s rigid connector features was also in part motivated by this project.

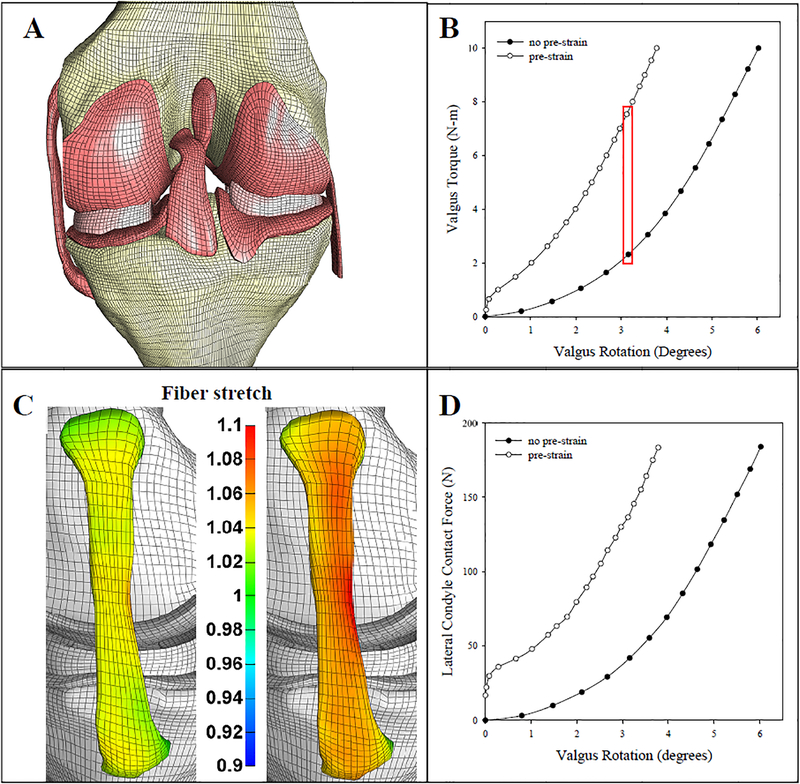
Figure 8:

Finite element analysis of the Open Knee model under 10 Nm of valgus torque. A) The Open Knee finite element model, including articular cartilage, menisci, and the four major knee ligaments. B) Valgus torque as a function of valgus rotation for both the prestrained model and the model without prestrain. The red box shows the two points where the fiber strains are compared in panel C. C) Effective fiber stretch at ~3.1 degrees valgus rotation. Left, without prestrain. Right, with prestrain. D) The contact reaction force across the lateral condyle. Results demonstrate that the structural behavior of the joint and predicted ligament strains are dramatically different without prestrain field to the ligaments, and in particular the response is too soft under valgus torque without prestrain.

6. FUTURE OF FEBIO

6.1. FEBio, a multi-physics solver

FEBio’s main priority continues to be the development of a software environment that is tailored to the specific needs of the biomechanics and biophysics communities. The initial focus of the project was mostly on solid mechanics. With the implementation of biphasic, and later multiphasic capabilities, including the modeling of an arbitrary number of solutes, electrokinetics and chemical reactions, FEBio has evolved into a true multi-physics code. This allows researchers to model and investigate the interactions between different types of physics within a single model. These capabilities are obviously important for solving problems in biophysics. Due to the importance of modeling multi-physics capabilities, the expansion of FEBio’s capabilities in this area is our current focus.

The modeling of fluids remains one of the biggest challenges of FEBio. Although fluids can be modeled in FEBio as components of mixtures, the explicit modeling of viscous fluid flows is not yet available. The modeling of computational fluid dynamics, and more significantly the incorporation of fluid-solid interactions, is very relevant to biomechanics and biophysics (e.g. cardiovascular mechanics, cerebrospinal mechanics, vocal fold and upper airway mechanics, viscous flow over endothelial cells, canalicular and lacunar flow around osteocytes, diarthrodial joint lubrication, and many applications in biomedical device design). Therefore the next stage of FEBio development efforts are focused on the implementation of algorithms that model computational fluid dynamics and fluid-solid interactions (FSI). To accommodate these features, FEBio’s linear and nonlinear solution algorithms will need to be expanded. In particular, the implementation of efficient iterative linear solvers and preconditioners will be essential.

As we expand the capabilities of FEBio into the fluid mechanics and FSI domains, adaptive mesh refinement (AMR, local mesh refinement and coarsening) will become a necessary feature. The accuracy of a FE solution is intimately tied to the discretization, since it determines the spatial resolution of both the geometry and the interpolation of field variables. As an example application motivating the need for AMR, high gradients in velocity for fluid mechanics simulations necessitate local refinement for both accuracy and sometimes local convergence as well. These areas are not always possible to identify before the analysis begins requiring the initial mesh to be refined during the analysis. Although AMR is available in some commercial and free FE packages for solid mechanics, it is much more of a necessity in CFD and FSI where the solution times may be very long and restarting an analysis with a new mesh is not practical. ALE type FSI algorithms generate a special necessity for mesh adaptivity at solid-fluid boundaries.

6.2. Center for Computational Biomechanics and Biophysics

The PIs of the FEBio project, Weiss and Ateshian, are currently in the process of setting up the Center for Computational Biomechanics and Biophysics (CCBB). The purpose of the center is to continue the development of FEBio and extend it in exciting new directions, but also to create new collaborations and widen the reach and impact of FEBio.

Aside from extending FEBio’s multi-physics capabilities, the integration of image data in FE analyses is another goal. This implies developing an entire modeling pipeline from image data, through segmentation and mesh generation, to FE analysis. In addition, this new capability would allow users to integrate image data directly into FE models, e.g. for specification of inhomogeneous material properties.

Another development effort will be focused on the expansion of the plugin framework such that FEBio could be coupled easily with other, domain-specific software. Also the support for scripting languages such as Python will allow users to easily develop new applications with FEBio.

The CCBB center will also focus on expanding our dissemination and training efforts. New education and training programs will be developed for our major target communities. This will entail developing new curricula for course-based education, specific tutorials and workshops for relevant audiences, and expanding our already extensive web-based documentation and online education tools.

7. ACKNOWLEDGMENTS

The development of FEBio was supported by the National Institute of General Medical Sciences of the National Institutes of Health under award number R01GM083925. The content of this article is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

The FEBio project has advanced thanks to the help of many contributors. We wish to express our special thanks to David Rawlins, who has been a member of the FEBio software development team since 2008 and has contributed, among other things, to the material optimization module, the distribution of the code and documentation, and the proper functioning of the forum and website. Others have contributed by implementing specific features, or offering valuable feedback that helped us address shortcomings that led to code improvements: Dr. Ben Ellis, Dr. Alexander Veress, Dr. Lowell Edgar, Dr. Sam Evans, Dr. Mike Puso, Dr. Ahmet Erdemir, Mr. Robert Nims, Mr. Chieh Hou. The FEBio project also received a generous donation from Dr. Siswanto from the Universiti Tun Hussein Onn Malaysia. Finally, we also wish to express our gratitude to our user community. The level of enthusiasm that we have received over the years has greatly exceeded our expectations. We appreciate the invaluable feedback that they have given us as this has in a profound manner helped us shape FEBio such that it will continue to be the preferred tool for solving computational problems in biomechanics and biophysics.