Skip to main content
PMC home page
PLOS ONE logoLink to PLOS ONE
. 2018 Sep 19;13(9):e0202141. doi: 10.1371/journal.pone.0202141

Tubulin's response to external electric fields by molecular dynamics simulations

Joshua J Timmons 1, Jordane Preto 2, Jack A Tuszynski 2,3,4, Eric T Wong 1,*
Editor: Claude Prigent5
PMCID: PMC6145594  PMID: 30231050

Abstract

Tubulin heterodimers are the building blocks of microtubules and disruption of their dynamics is exploited in the treatment of cancer. Electric fields at certain frequencies and magnitudes are believed to do the same. Here, the tubulin dimer’s response to external electric fields was determined by atomistic simulation. External fields from 50 to 750 kV/cm, applied for 10 ns, caused significant conformational rearrangements that were dependent upon the field’s directionality. Charged and flexible regions, including the α:H1-B2 loop, β:M-loop, and C-termini, were susceptible. Closer inspection of the α:H1-B2 loop in lower strength fields revealed that these effects were consistent and proportional to field strength, and the findings indicate that external electric fields modulate the stability of microtubules through conformational changes to key loops involved in lateral contacts. We also find evidence that tubulin’s curvature and elongation are affected, and external electric fields may bias tubulin towards depolymerization.

Introduction

α- and β- tubulin heterodimers spontaneously assemble end to end to form protofilaments, and the helical arrangement of 13 protofilaments constitutes microtubules that are central to cellular rigidity, division, motility, and trafficking of intracellular proteins [1–4]. As the driving force for sister chromatid segregation in mitosis, microtubules have long been targeted by chemotherapies using pharmacological agents that stabilize MTs such as paclitaxel, and those that destabilize them such as vincristine, and vinblastine [5,6]. More recently, microtubules have become the target of a novel treatment modality: electric fields. Alternating electric fields at 2.5 V/cm with a frequency of 100–300 kHz, known as Tumor Treating Fields (TTFields), disrupt microtubules in vitro. While no definitive mechanistic model of their action has been established, a putative explanation claims that this is due to the microtubules’ large intrinsic charge and dipole [7–10] which interacts with electric fields and their gradients. In a major development in the area of cancer therapy, Optune®, a device for administering the fields to patients, was recently approved by the FDA to treat glioblastoma [11–13].

Compared to TTFields, external electric fields (EEFs) of much greater strengths but shorter timescales can also eliminate cancer cells in vitro and in vivo. Nanosecond pulsed electric fields (nsPEFs)—static EEFs of tens of kV/cm that are applied repeatedly over nanosecond durations [14,15]—have demonstrated anti-cancer potential against Jurkat and HL-60 cells in vitro at 300 kV/cm [15], papillomas and squamous cell carcinoma in vivo at 40 kV/cm [16], and many other cancer models [17–23]. Several mechanisms have been proposed to explain nsPEFs’ effects, but their creation of nanopores, which allow an influx of Ca2+ from extracellular and intracellular sources, and reduction of mitochondrial membrane potential have received the most attention [14,24,25].

More recent investigations have demonstrated that nsPEFs affect the cytoskeleton. Nanosecond pulsed electric fields cause a breakdown of actin filaments with concomitant cell rounding [26–29] and 44 kV/cm pulses induce microtubule clearance in U87 human glioblastoma cells within minutes, all without observable Ca2+ influx and/or osmotic swelling [30]. These findings of microtubule breakdown [30], in conjunction with those of Kirson et al. [31] in TTFields, suggest that EEFs may destabilize microtubules directly in addition to various indirect effects that have been proposed [8].

Other investigations of tubulin in EEFs have found that microtubules can be aligned with an applied electric field [32,33] and that EEFs reduce the Young’s modulus of a tubulin heterodimer [34]. Despite these earlier findings, the precise atomic-level details of a single dimer’s response to EEFs are unknown. Therefore, we performed an investigation of these effects through Molecular Dynamics, applying EEFs along multiple directions (Fig 1) at time scales and field strengths consistent with nsPEFs (36–38), the results of which are important for understanding macroscopic observations like nsPEF-induced depolymerization. Notably, the α:H1-B2 loop and β:M-loop, that are integral to lateral contacts between protofilaments, are especially susceptible to the influence of electric fields, and the bend angle and elongation of tubulin are affected, which may accelerate the depolymerization process.

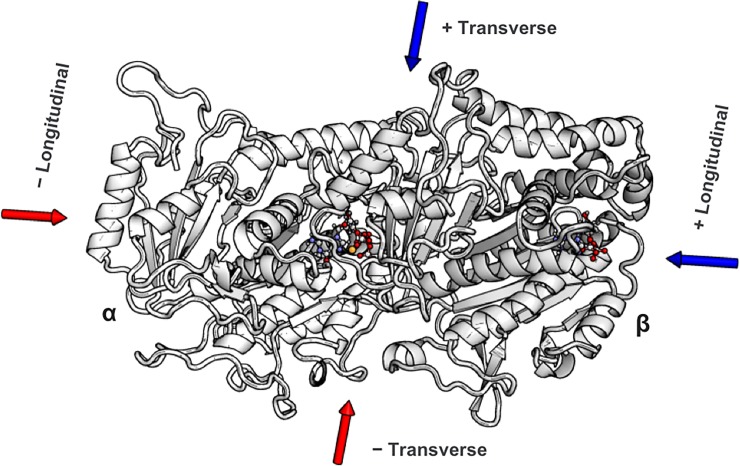
Fig 1. Directionality of the applied electric fields.

Fig 1

Open in a new tab

Electric fields were applied along the direction of the dipole (transverse axis) and along the vector between the beta and alpha monomers’ center of mass (longitudinal axis), both in reference to the equilibrated dimer’s initial position.

Results and discussion

Tubulin’s structure and dynamics are affected by EEFs

Structural change as measured by root mean standard deviation

We first investigated large-scale EEF-induced changes to tubulin’s root mean standard deviation (RMSD) and dipole magnitude. By both measurements, a 750 kV/cm EEF caused significant structural changes in all directions tested (Fig 2). Most of the change in RMSD was in loops and turns. As expected, we found that rigid structures like alpha helices and beta sheets remained relatively fixed, with an RMSD for alpha carbons close to 1 Å, whereas other structural motifs were more sensitive to the EEFs and exhibited an RMSD of 5–6 Å. By comparison, the same flexible motifs showed an RMSD of around 2–3 Å in the dimer unexposed to an EEF. These more-flexible residues were classified as, in order of prevalence, coils, hydrogen bonded turns, and 310 helices (Fig 2B and Fig 2E). The relaxation time was less than 30 ns, when the EEF was applied along the dimer’s transverse axis (Fig 2A), but lasted longer when applied along the longitudinal axis (Fig 2D). Microtubules clearance is observable in nsPEFs applied at 10 Hz, or with 100 ms between their application, which means that there is likely sufficient time for total relaxation in a single dimer between pulses.

Fig 2. Structural rearrangement in the presence of a strong EEF.

Fig 2

Open in a new tab

Cα RMSD of a tubulin dimer in the transverse (a) and longitudinal (d) directions. Cα RMSD again but with delineation of displacement in alpha helices and beta sheets versus other structures in the transverse (b) and longitudinal (e) directions. Total dimer dipole magnitudes for the transverse (c) and longitudinal (f) directions.

Increase of dipole moment by EEFs

In all but the negative transverse direction, or opposite the dimer’s dipole, the EEF doubled the magnitude of tubulin’s dipole moment (Fig 2C and Fig 2F). Increases in dipoles were longer lasting when the EEF was applied along the longitudinal versus transverse axis, a finding similar to our results in RMSD (Fig 2C and Fig 2F). This effect is explainable by coupling of charged residues with the EEF, in which the dimers’ natural charge distributions were exaggerated (in all but the negative transverse simulation). Atomistic simulations of insulin and lysozyme in EEFs have demonstrated that protein dipoles are affected by the localized rearrangement of charged sidechains and loops [35–37]. Additionally, Ojeda-May et al [38] and Budi et al [36] found that EEFs can convert beta sheets to alpha helices or destabilize alpha helices, respectively, but we observed neither in the 750 kV/cm EEFs studied here (S1 Fig).

Rearrangement is greatest in the α:H1-B2 Loop, β:H6-H7 Loop, and C-termini

Charged, flexible regions undergo large per-residue displacement

To gain a better understanding of EEFs’ effects on the tubulin dimer, we superimposed final structures, after 10 ns of EEF exposure in opposite directions, and calculated displacement on a residue-by-residue basis. In flexible regions, structural rearrangement was dependent upon the residue’s root mean square fluctuation (RMSF) (S2 Fig) and charge; positive and negative residues move towards the EEF’s anode and cathode, respectively. There was overlap in the affected regions within dimers in the transverse and longitudinal EEFs. After exposure to EEFs along the dimer’s transverse axis (Fig 3B), displacement was greatest in the α:H1-B2 loop (Fig 3D), α:H4-B5 loop, β:H6-H7 loop (Fig 3C), β:M-loop, and C-termini of both monomers (Fig 3E). Similarly, the longitudinal EEFs greatly affected the α:H1-B2 loop (Fig 4C), β:H6-H7 loop, β:M-loop (Fig 4E), and both C-termini (Fig 4D).

Fig 3. Displacement induced by transverse electric fields.

Fig 3

Open in a new tab

(A) Displacement distance (Å) of Cα atoms between final tubulin structures after 10 ns of 750 kV/cm in the positive and negative transverse directions (after superimposition of structures). (B) Displacements exceeding 2 angstroms are visualized by vectors from the residues in the initial, equilibrated structure (white) to the final structure after application along the negative direction (red arrows) and the positive direction (blue arrows). For clarity, every other displacement vector is shown. (C, D, E) Final positions of the dimer are visualized after 750 kV/cm in the negative (red) and positive (blue) transverse directions for the β:H6-H7 Loop, α:H1-B2 Loop, and β:C-terminus. Positively and negatively charged residue side chains are represented by light-blue and yellow sticks, respectively.

Fig 4. Displacement induced by longitudinal electric fields.

Fig 4

Open in a new tab

(A) Analogous to Fig 3, but comparing displacement between structures after application of longitudinal EEFs. (B) Displacement vectors are shown from every other Cα, for clarity. (C, D, E) Final positions are visualized for the heterodimer after 750 kV/cm in the negative (red) and positive (blue) longitudinal directions for the α:H1-B2 Loop, C-termini, and M-loop.

C-termini exposed to EEFs showed large movements relative to those that were unexposed, but the extent of their rearrangement was dependent on the field’s direction. While the C-termini of the α-monomer and β-monomer shifted inwards in the positive and negative longitudinal EEF, respectively, neither were significantly displaced when the EEF was applied along the opposite, outward direction (Fig 4B). This, plus other research indicating that there are frequent interactions between each monomer’s C-terminus and the other’s H11 [39], suggests that the C-termini take an “inward” trajectory from a position on the surface of the dimer. In opposition to this movement is the attraction between the negative C-termini and the dimer’s positively charged surface. Our equilibrated structure contained salt bridges from α:311K to α:447E and β:292K to β:445E (S3 Fig); the C-termini would necessarily need to escape their attraction to the dimer’s positive surface along an inward low-energy path and the EEFs’ direction influences whether they reach such an extended state.

EEF-induced modulation of C-termini would have biological relevance because of effects on the dynamics of kinesin [40], dynesin [41], and other microtubule-associated proteins, all of which directly interact with the C-termini of microtubules. In fact, post-translational modifications and removal of the C-termini have already been implicated in changes to motor protein velocity and processivity [41,42]. The interaction between the C-termini and EEFs may be further complicated by post-translational modifications. One such modification is polyglutamylation, which is common to cancer cells, and would result in the addition of negatively charged glutamate amino acids to the already negatively charged C-termini [43] making the latter protrude even more from the mostly negatively charged surface of microtubules. Further investigations of the C-termini’s response to EEFs are needed to characterize their transition between contracted and extended states [44] and whether such changes affect the dynamics of microtubule-associated proteins.

Per-residue fluctuations are augmented in EEFs

We also investigated how EEFs affect residue fluctuations. We calculated change in RMSF as ΔRMSF = RMSFEEF − RMSFAMB where RMSFEEF represents fluctuations of each residue in the dimer exposed to an EEF and RMSFAMB denotes fluctuations in dimer unexposed to an EEF. Therefore, a residue with a large positive ΔRMSF experienced a significant increase in its fluctuation in an external electric field (relative to the same residue in the dimer unexposed to an external electric field); conversely, a residue with a large negative ΔRMSF was found to have stabilized by the field. The results (Fig 5 and S4 Fig) further demonstrate the interaction between EEFs and the α:H1-B2 loop, α:H10-B9 loop, M-loop, and C-termini. For these regions, the EEFs’ influence on |ΔRMSF| was consistent, regardless of the direction in which the EEF was applied, but whether ΔRMSF was positive or negative was variable. For example, there was an increase in fluctuation for the M-loop in both the positive transverse and, especially, negative longitudinal directions. But the same loop showed reduced fluctuation in the negative transverse and positive longitudinal directions. The directional dependence was most apparent in the α:H1-B2 loop which, for three of the four directions tested, experienced the greatest increase in fluctuation among all internal structures, yet was rigidified in the positive transverse EEF.

Fig 5. Change in per-residue RMSF.

Fig 5

Open in a new tab

Changes in residue fluctuations for a tubulin dimer in a 750 kV/cm external electric field compared to a tubulin dimer not exposed to an external electric field (ΔRMSF = RMSFEEF − RMSFAMB). The positive transverse (blue) and negative transverse ΔRMSF plots are along the top row, while the positive longitudinal (blue) and negative longitudinal (red) ΔRMSF plots are along the bottom.

EEF perturbation results are consistent at lower magnitudes

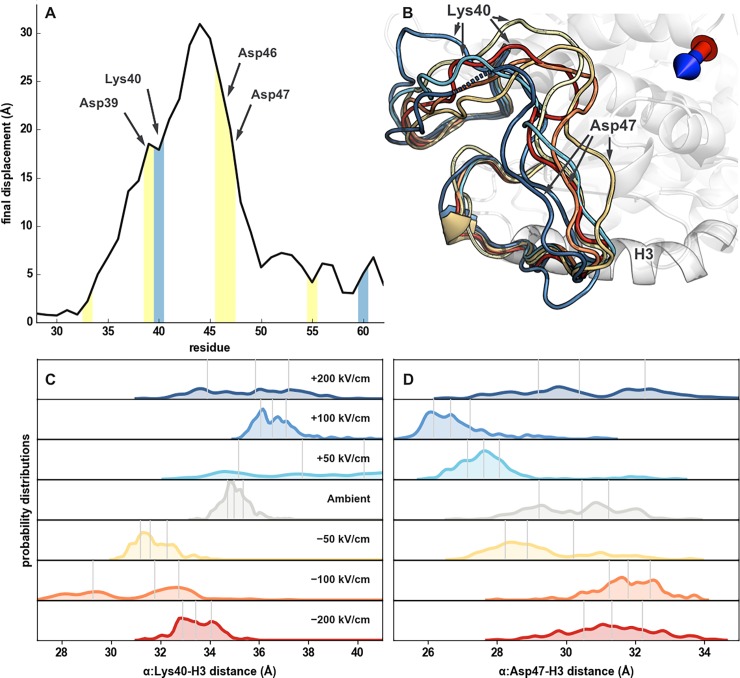
Given its notable susceptibility to 750 kV/cm EEFs, measurable by both displacement and ΔRMSF, we examined the robustness of α:H1-B2 loop’s response to EEFs of lower strengths. We ran 10 ns simulations of EEFs applied along the positive and negative transverse directions at 50, 100, and 200 kV/cm and then visualized the average positions of the loop over the last 5 ns (Fig 6B). We also characterized the loop’s movement using measurements of two charged amino acids—greater distances between α:40K and α:H3 (Fig 6C) and α:47D and α:H3 (Fig 6D) correspond to outward movements of the first and second half of the α:H1-B2 loop, respectively. Inspection of the α:H1-B2 loop’s response to lower strength EEFs revealed a change in conformation that was proportional to field strength. The greatest effect was observed in the movements of α:40K.

Fig 6. α:H1-B2 Loop’s response to transverse external electric fields.

Fig 6

Open in a new tab

(A) Final per-residue displacement, after application a 750 kV/cm EEF along the transverse axis, between a dimer exposed to a positive and negative transverse direction. Negatively and positively charged residues are highlighted with yellow and light-blue, respectively. (B) Average positions of the α:H1-B2 loop, during the final 5 ns of EEF application, along the transverse direction. Loop colors of dark blue, blue, light blue, yellow, light orange, orange, and red correspond to +200, +100, +50, 0, -50, -100, and -200 kV/cm field strengths, respectively. The positive and negative EEF directions are indicated with a blue and red arrowhead, respectively. (C, D) Probability distributions for the distance between α:40K and α:H3 and between α:47D and α:H3, using snapshots from the final 5 ns of EEF exposure, correspond to outward movement of the first and second half of the α:H1-B2 loop, respectively. Quartiles for distance measurements are indicated with vertical gray lines.

As a positively charged residue, α:40K was more frequently in an “outward” conformation in a positive transversal field and vice versa, even at 50 kV/cm (Fig 6C). Conversely, the negatively charged α:Asp47 was more likely to be in an “inward,” closer to the dimer conformation in a positive transverse EEF. Given the field magnitudes and exposure duration tested here, the results indicate that nsPEFs induce rearrangement in the α:H1-B2 loop. The findings are relevant to a mechanistic explanation of the breakdown of microtubules under the influence of EEFs.

A tubulin dimer in a microtubule is held in place through loop-loop interactions. A dimer within a microtubule has both longitudinal and lateral contacts with its own and adjacent protofilaments, respectively [4,45,46]. In the energetically favorable B-lattice confirmation, lateral contacts between the α monomers of two protofilaments include hydrogen bonds between the H1-B2 loop on one side and the M-loop on the other [47,48]. Similarly, lateral contacts between β monomers include hydrogen bonds between the M-loop of one dimer and the H1-B2 loop of the other [2,4,47]. Given that these regions are susceptible to EEFs, we conjecture that this induced rearrangement may promote microtubule catastrophe.

Tubulin’s essential dynamics are affected by EEFs

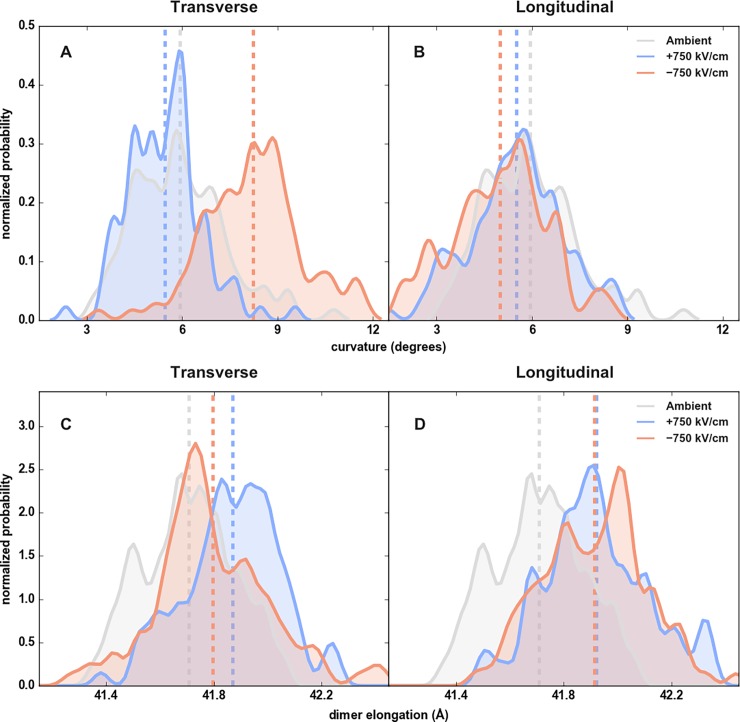
Beyond the per-residue effects of EEFs, we asked whether the lower-frequency motions of tubulin were also affected. Specifically, intradimer curvature and elongation are two modes that are biologically relevant for the polymerization and depolymerization of microtubules [49,50]. These two essential modes in microtubule dynamics were calculated over the last 5 ns of exposure to 750 kV/cm EEFs for all field directions (Fig 7). The negative transverse EEF promoted the greatest change in curvature, with the mean bend angle at 5.9° and 8.2° for the unexposed and negative transverse EEF, respectively (Fig 7B). Furthermore, EEFs in all four directions promoted elongation, though the greatest increases were in the longitudinal EEFs (Fig 7D).

Fig 7. Tubulin essential dynamics in an external electric field.

Fig 7

Open in a new tab

(A, B) Normalized probability distributions of tubulin’s curvature and dimer elongation for the last 5 nanoseconds of EEF application. Curvature was calculated by the method presented in [51]. Elongation was measured as the distance between the center of mass of each monomer’s alpha helices. Mean curvature and compaction are shown by dashed lines.

The curvature of tubulin has long been linked to the dynamics of microtubules. The straight conformation is found in zinc-induced protofilament sheets [52] and are characteristic of stable microtubules [2], while the curved conformation is found in depolymerization peels, which are sometimes referred to in the literature as “ram’s horns” [4,53]. A recent model, based on structures produced with cryo-electron microscopy, proposed that the curved dimer conformation is an energetically preferred state that alleviates the strain of elongation produced during the depolymerization process [4]. Given our findings that EEFs can bias tubulin dimers towards bent (Fig 7B) and elongated conformations (Fig 7D), we posit that modulation of essential dynamics is another means by which nsPEFs affect microtubule stability.

While our model investigates the effects of EEFs on a single tubulin dimer, other groups have proposed that nsPEFs’ effects on the cytoskeleton are due to electrophoresis of the large, negatively charged microtubules [30]. In other words, microtubule breakdown in nsPEFs stems from macro-scale forces, because an unaligned microtubule experiences a lateral electrophoretic force in electric fields [54], and the breakdown of loop-loop interactions occurs secondarily. We did observe an increase in the mean squared displacements of dimers that were proportional to the EEFs’ magnitude (S5 Fig), but insight into large-scale, electrophoretic breakdown of microtubules would require either a macroscopic model of microtubule networks or an in vitro experiment on microtubule buckling in a range of external electric fields. Relatedly, buckling during the alignment process appears to be modulated by loop-loop interactions between adjacent protofilaments, as evidenced by microtubule response to acetylation of α:40K [55]—so EEF-induced changes in loop-orientation may affect microtubules’ plasticity and resistance to buckling at the level of the dimer. Future experiments may further this work by increasing tubulin’s number—by simulating either a full or partial cross-section of a microtubule with lateral contacts [48]—or by investigating the effects of hydrolysis of GTP on the dimer’s response to EEFs.

Conclusions

In this paper, we have reported on our computer simulations of the effects of externally applied alternative electric fields on the structure and dynamics of tubulin dimers. This was motivated by several experimental observations concluding that microtubules become unstable when exposed to sufficiently strong electric fields. In our simulations, we have observed displacement in the charged and flexible regions of tubulin, including the α:H1-B2 loop, β:M-loop, and C-termini. The changes to the α:H1-B2 loop were persistent at lower magnitude EEFs, and there were also detectable perturbations to tubulin’s curvature and elongation. Based on these observations, we propose a mechanistic explanation of the microtubule breakdown in EEFs, which is most likely to involve promotion of depolymerization through weakened lateral bonds and increased dimer strain. Finally, we have found significant effects of the field’s orientation on the conformational rearrangements of tubulin dimers, an observation that should encourage an experimental validation.

Materials and methods

We created a 3D model of a tubulin heterodimer by modifying a crystal structure of tubulin bound to Taxol: PDB ID: 1JFF [56]. Preparing this structure for computer simulations, we removed Taxol, added missing residues α:1, α:35–60, α:440–451, β:1, and β:428–445, and energy minimized using Modeller [57].

Note that the residue indices referenced here are ungapped and therefore differ from those reported by Löwe et al [56]. The final structure included the dimer’s C-termini and consisted of 451 residues in α-tubulin plus GTP and one Mg2+ atom, both of which are bound to α-tubulin, and 445 residues in β-tubulin plus GDP, which is bound to β-tubulin. We included missing hydrogen atoms and delta protonated histidine residues with psfgen [58]. We then solvated the dimer in TI3P3 water atoms in a rectangular box with 20 Å of padding along each axis using VMD’s Solvate plugin. This box sizing was chosen with consideration of C-terimini movements to prevent interaction with the dimer’s image. To neutralize the dimer and produce a NaCl molarity of 150mM, we added 185 Chloride and 240 Sodium ions via VMD’s Autoionize plugin; ultimately, the periodic cell was 110 x 150 x 110 Å along the x, y, and z axes, respectively, and contained 164,493 water atoms.

Long-range electrostatics effects were treated with Particle-Mesh Ewald sum and a 12 Å cutoff [59]. We applied rigid bonds to hydrogen bonds, used a 2 femtosecond timestep, and saved frames to trajectories every 25 ps. We energy minimized the solvated structure for 25 ps, equilibrated it for 500 ps in an NVT ensemble, then equilibrated it for 1 nanosecond in an NPT ensemble. Because of 1JFF’s unfavorable initial conformation, we performed extensive additional energy minimization of the dimer by running it for an additional 100 ns in an NPT ensemble until convergence was definitive in RMSD. All simulations were run with the CHARMM36 force field [60]. Notably, CHARMM36 is a non-polarizable force field in which dipoles are measured purely by the distribution of fixed charges. In future studies, electronic polarization by the EEF and or other modalities could be accounted for with a polarizable force field like Drude-2013 or AMOEBA-2013 [61–63]. NAMD 2.10 [64] was used to run the simulations on clusters of 64 nodes, each containing 16 cores, connected by Infiniband in a BlueGene/Q cluster. We ran equilibration and production simulations at 310°K and coupled them to a Nosé-Hoover-Langevin piston for pressure control and used Langevin dynamics for temperature control.

We simulated static electric fields with the External Electric Field module of NAMD and applied them along four directions that we define as the positive and negative of the transverse and longitudinal axes, respectively (Fig 1). The positive transverse direction was that of the dimer’s dipole moment at the start of the production runs while the negative transverse direction was its negative. The positive longitudinal direction was along the vector formed from the beta to the alpha monomers’ center of mass at the beginning of the production runs; here again, the negative longitudinal vector was its negative. In addition to the control run, we ran simulations of EEFs at 750 kV/cm along each of the four major directions; we chose this initial magnitude based on other Molecular Dynamics studies of proteins in EEFs found in the literature [35,65,66]. We performed each production run for 50 ns and applied the EEFs between the 10 and 20 ns time points (using a 10 ns duration that is typical of nsPEFs [30]). Additionally, we simulated lower strength fields at 200, 100, and 50 kV/cm along the two transverse directions for 10 ns using the positions and velocities of the ambient production run at the ten-nanosecond mark for the first frame.

Analysis was performed with modules and scripting in VMD [58]. Per-residue displacement, referred to here as “final displacement,” was calculated as the distance between alpha carbons after superimposing heterodimers exposed to two EEFs of opposite directionality, which is loosely based on the concept developed by Hekstra et al [67]. Tubulin’s intradimer curvature (or bend angle) was calculated by the method described by Pecquer et al [51] and characterized by Peng et al [53]. Briefly, we calculated curvature as the intersection angle between the two best fit lines—created with the atoms of α:H7 and β:H7—from the Taxol bound tubulin dimer, PDB ID: 1JFF, and the dimer under study, after superimposing the two structures by the atoms of their α:H7s. We measured dimer elongation as the distance between the centers of mass from all alpha helices atoms in the α and β monomers, using atoms classified as belonging to alpha helices in the initial equilibrated structure.

Supporting information

S1 Fig. Secondary residue classifications in a 750 kV/cm EEF.

(A, B) The total number of residues that are classified as alpha helices or beta sheets during the application of 750 kV/cm EEFs of four directions: positive transverse, negative transverse, positive longitudinal, and negative longitudinal.

(TIFF)

Click here for additional data file. (6.6MB, tiff)
S2 Fig. Final displacement in a transverse external electric field and RMSF.

Final displacement, measured as the distance between residues after 10 ns exposure to a positive and negative transverse EEF (black). Cα RMSF per residue of a tubulin heterodimer, from the 10 to 20 ns time frame, without exposure to an EEF (blue).

(TIFF)

Click here for additional data file. (3.3MB, tiff)
S3 Fig. Salt bridges between the C-termini and the dimer surface.

Representative salt bridges experienced by the C-termini when in a contracted state (lying along the dimer’s surface). A distance cutoff of 3.2 Å and the positions of the initial frame, after equilibration, were used to identify possible salt bridges.

(TIFF)

Click here for additional data file. (3.6MB, tiff)
S4 Fig. Visualization of change in per-residue RMSF.

Same as Fig 4 but with ΔRMSF of each residue mapped onto the structure. Red and blue indicate an increase and decrease in RMSF, respectively. Field directions are indicated with arrows.

(TIFF)

Click here for additional data file. (5.7MB, tiff)
S5 Fig. Mean standard displacement of tubulin in a transverse external electric field.

Mean standard displacement (Å2) of tubulin from the start to the end of the application of a transverse EEF.

(TIFF)

Click here for additional data file. (3.5MB, tiff)

Data Availability

The code used for analysis is available on Github at: https://github.com/JJTimmons/tubulin-in-an-EEF. Data is also available on FigShare at (DOI: https://figshare.com/s/32bd5a62009f184ebd47)

Funding Statement

This work was supported by A Reason to Ride research fund (http://areasontoride.com/). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

References

  • 1.Janke C. The tubulin code: Molecular components, readout mechanisms, and functions. J Cell Biol. 2014;206: 461–472. 10.1083/jcb.201406055 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Li H, DeRosier DJ, Nicholson WV, Nogales E, Downing KH. Microtubule Structure at 8 Å Resolution. Structure. 2002;10: 1317–1328. 10.1016/S0969-2126(02)00827-4 [DOI] [PubMed] [Google Scholar]
  • 3.Tuszyński JA, Hameroff S, Satarić MV, Trpisová B, Nip MLA. Ferroelectric behavior in microtubule dipole lattices: Implications for information processing, signaling and assembly/disassembly. J Theor Biol. 1995;174: 371–380. 10.1006/jtbi.1995.0105 [DOI] [Google Scholar]
  • 4.Alushin GM, Lander GC, Kellogg EH, Zhang R, Baker D, Nogales E. High-Resolution Microtubule Structures Reveal the Structural Transitions in αβ-Tubulin upon GTP Hydrolysis. Cell. 2014;157: 1117–1129. 10.1016/j.cell.2014.03.053 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Dumontet C, Jordan MA. Microtubule-binding agents: a dynamic field of cancer therapeutics. Nat Rev Drug Discov. 2010;9: 790–803. 10.1038/nrd3253 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Gigant B, Wang C, Ravelli RBG, Roussi F, Steinmetz MO, Curmi PA, et al. Structural basis for the regulation of tubulin by vinblastine. Nature. 2005;435: 519–522. 10.1038/nature03566 [DOI] [PubMed] [Google Scholar]
  • 7.Kirson ED, Dbaly V, Tovarys F, Vymazal J, Soustiel JF, Itzhaki A, et al. Alternating electric fields arrest cell proliferation in animal tumor models and human brain tumors. Proc Natl Acad Sci. 2007;104: 10152–10157. 10.1073/pnas.0702916104 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Tuszynski J, Wenger C, Friesen D, Preto J. An Overview of Sub-Cellular Mechanisms Involved in the Action of TTFields. Int J Environ Res Public Health. 2016;13: 1128 10.3390/ijerph13111128 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Tuszynski JA. Electromagnetic fields and optomechanics in cancer diagnostics and treatment. Front Biosci. 2018;23: 1391–1406. 10.2741/4651 [DOI] [PubMed] [Google Scholar]
  • 10.Gera N, Yang A, Holtzman TS, Lee SX, Wong ET, Swanson KD. Tumor Treating Fields Perturb the Localization of Septins and Cause Aberrant Mitotic Exit. Prigent C, editor. PLOS ONE. 2015;10: e0125269 10.1371/journal.pone.0125269 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Stupp R, Wong ET, Kanner AA, Steinberg D, Engelhard H, Heidecke V, et al. NovoTTF-100A versus physician’s choice chemotherapy in recurrent glioblastoma: A randomised phase III trial of a novel treatment modality. Eur J Cancer. 2012;48: 2192–2202. 10.1016/j.ejca.2012.04.011 [DOI] [PubMed] [Google Scholar]
  • 12.Stupp R, Taillibert S, Kanner AA, Kesari S, Steinberg DM, Toms SA, et al. Maintenance Therapy With Tumor-Treating Fields Plus Temozolomide vs Temozolomide Alone for Glioblastoma: A Randomized Clinical Trial. JAMA. 2015;314: 2535 10.1001/jama.2015.16669 [DOI] [PubMed] [Google Scholar]
  • 13.Stupp R, Taillibert S, Kanner A, Read W, Steinberg DM, Lhermitte B, et al. Effect of Tumor-Treating Fields Plus Maintenance Temozolomide vs Maintenance Temozolomide Alone on Survival in Patients With Glioblastoma: A Randomized Clinical Trial. JAMA. 2017;318: 2306 10.1001/jama.2017.18718 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Beebe S, Sain N, Ren W. Induction of Cell Death Mechanisms and Apoptosis by Nanosecond Pulsed Electric Fields (nsPEFs). Cells. 2013;2: 136–162. 10.3390/cells2010136 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Beebe SJ, Fox PM, Rec LJ, Willis ELK, Schoenbach KH. Nanosecond, high-intensity pulsed electric fields induce apoptosis in human cells. FASEB J. 2003;17: 1493–1495. 10.1096/fj.02-0859fje [DOI] [PubMed] [Google Scholar]
  • 16.Yin D, Yang WG, Weissberg J, Goff CB, Chen W, Kuwayama Y, et al. Cutaneous Papilloma and Squamous Cell Carcinoma Therapy Utilizing Nanosecond Pulsed Electric Fields (nsPEF). Rubinsky B, editor. PLoS ONE. 2012;7: e43891 10.1371/journal.pone.0043891 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Chen X, Kolb JF, Swanson RJ, Schoenbach KH, Beebe SJ. Apoptosis initiation and angiogenesis inhibition: melanoma targets for nanosecond pulsed electric fields: nsPEFs targets apoptosis and angiogenesis. Pigment Cell Melanoma Res. 2010;23: 554–563. 10.1111/j.1755-148X.2010.00704.x [DOI] [PubMed] [Google Scholar]
  • 18.Garon EB, Sawcer D, Vernier PT, Tang T, Sun Y, Marcu L, et al. In vitro andin vivo evaluation and a case report of intense nanosecond pulsed electric field as a local therapy for human malignancies. Int J Cancer. 2007;121: 675–682. 10.1002/ijc.22723 [DOI] [PubMed] [Google Scholar]
  • 19.Miao X, Yin S, Shao Z, Zhang Y, Chen X. Nanosecond pulsed electric field inhibits proliferation and induces apoptosis in human osteosarcoma. J Orthop Surg. 2015;10: 104 10.1186/s13018-015-0247-z [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Nuccitelli R, Tran K, Sheikh S, Athos B, Kreis M, Nuccitelli P. Optimized nanosecond pulsed electric field therapy can cause murine malignant melanomas to self-destruct with a single treatment. Int J Cancer. 2010;127: 1727–1736. 10.1002/ijc.25364 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Ren Z, Chen X, Cui G, Yin S, Chen L, Jiang J, et al. Nanosecond Pulsed Electric Field Inhibits Cancer Growth Followed by Alteration in Expressions of NF-κB and Wnt/β-Catenin Signaling Molecules. Agoulnik IU, editor. PLoS ONE. 2013;8: e74322 10.1371/journal.pone.0074322 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Wang J, Guo J, Wu S, Feng H, Sun S, Pan J, et al. Synergistic Effects of Nanosecond Pulsed Electric Fields Combined with Low Concentration of Gemcitabine on Human Oral Squamous Cell Carcinoma In Vitro. Rishi A, editor. PLoS ONE. 2012;7: e43213 10.1371/journal.pone.0043213 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Yin S, Chen X, Hu C, Zhang X, Hu Z, Yu J, et al. Nanosecond pulsed electric field (nsPEF) treatment for hepatocellular carcinoma: A novel locoregional ablation decreasing lung metastasis. Cancer Lett. 2014;346: 285–291. 10.1016/j.canlet.2014.01.009 [DOI] [PubMed] [Google Scholar]
  • 24.Beebe SJ, White J, Blackmore PF, Deng Y, Somers K, Schoenbach KH. Diverse Effects of Nanosecond Pulsed Electric Fields on Cells and Tissues. DNA Cell Biol. 2003;22: 785–796. 10.1089/104454903322624993 [DOI] [PubMed] [Google Scholar]
  • 25.Semenov I, Xiao S, Pakhomov AG. Primary pathways of intracellular Ca2+ mobilization by nanosecond pulsed electric field. Biochim Biophys Acta BBA—Biomembr. 2013;1828: 981–989. 10.1016/j.bbamem.2012.11.032 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Dutta D, Asmar A, Stacey M. Effects of nanosecond pulse electric fields on cellular elasticity. Micron. 2015;72: 15–20. 10.1016/j.micron.2015.01.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Stacey M, Stickley J, Fox P, Statler V, Schoenbach K, Beebe S., et al. Differential effects in cells exposed to ultra-short, high intensity electric fields: cell survival, DNA damage, and cell cycle analysis. Mutat Res Toxicol Environ Mutagen. 2003;542: 65–75. 10.1016/j.mrgentox.2003.08.006 [DOI] [PubMed] [Google Scholar]
  • 28.Stacey M, Fox P, Buescher S, Kolb J. Nanosecond pulsed electric field induced cytoskeleton, nuclear membrane and telomere damage adversely impact cell survival. Bioelectrochemistry. 2011;82: 131–134. 10.1016/j.bioelechem.2011.06.002 [DOI] [PubMed] [Google Scholar]
  • 29.Thompson GL, Roth C, Tolstykh G, Kuipers M, Ibey BL. Disruption of the actin cortex contributes to susceptibility of mammalian cells to nanosecond pulsed electric fields: Actin Cortex Disruption by nsPEF. Bioelectromagnetics. 2014;35: 262–272. 10.1002/bem.21845 [DOI] [PubMed] [Google Scholar]
  • 30.Carr L, Bardet SM, Burke RC, Arnaud-Cormos D, Leveque P, O’Connor RP. Calcium-independent disruption of microtubule dynamics by nanosecond pulsed electric fields in U87 human glioblastoma cells. Sci Rep. 2017;7: 41267 10.1038/srep41267 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Kirson ED, Gurvich Z, Schneiderman R, Dekel E, Itzhaki A, Wasserman Y, et al. Disruption of Cancer Cell Replication by Alternating Electric Fields. Cancer Res. 2004;64: 3288–3295. 10.1158/0008-5472.CAN-04-0083 [DOI] [PubMed] [Google Scholar]
  • 32.Kim T, Kao M-T, Hasselbrink EF, Meyhöfer E. Active Alignment of Microtubules with Electric Fields. Nano Lett. 2007;7: 211–217. 10.1021/nl061474k [DOI] [PubMed] [Google Scholar]
  • 33.Kim T, Kao M-T, Hasselbrink EF, Meyhöfer E. Nanomechanical Model of Microtubule Translocation in the Presence of Electric Fields. Biophys J. 2008;94: 3880–3892. 10.1529/biophysj.107.112755 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Saeidi HR, Lohrasebi A, Mahnam K. External electric field effects on the mechanical properties of the αβ-tubulin dimer of microtubules: a molecular dynamics study. J Mol Model. 2014;20 10.1007/s00894-014-2395-1 [DOI] [PubMed] [Google Scholar]
  • 35.English NJ, Solomentsev GY, O’Brien P. Nonequilibrium molecular dynamics study of electric and low-frequency microwave fields on hen egg white lysozyme. J Chem Phys. 2009;131: 035106 10.1063/1.3184794 [DOI] [PubMed] [Google Scholar]
  • 36.Budi A, Legge FS, Treutlein H, Yarovsky I. Electric Field Effects on Insulin Chain-B Conformation. J Phys Chem B. 2005;109: 22641–22648. 10.1021/jp052742q [DOI] [PubMed] [Google Scholar]
  • 37.Budi A, Legge FS, Treutlein H, Yarovsky I. Effect of Frequency on Insulin Response to Electric Field Stress. J Phys Chem B. 2007;111: 5748–5756. 10.1021/jp067248g [DOI] [PubMed] [Google Scholar]
  • 38.Ojeda-May P, Garcia ME. Electric Field-Driven Disruption of a Native β-Sheet Protein Conformation and Generation of a Helix-Structure. Biophys J. 2010;99: 595–599. 10.1016/j.bpj.2010.04.040 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Freedman H, Luchko T, Luduena RF, Tuszynski JA. Molecular dynamics modeling of tubulin C-terminal tail interactions with the microtubule surface. Proteins Struct Funct Bioinforma. 2011;79: 2968–2982. 10.1002/prot.23155 [DOI] [PubMed] [Google Scholar]
  • 40.Okada Y, Hirokawa N. Mechanism of the single-headed processivity: Diffusional anchoring between the K-loop of kinesin and the C terminus of tubulin. Proc Natl Acad Sci. 2000;97: 640–645. 10.1073/pnas.97.2.640 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Wang Z, Sheetz MP. The C-Terminus of Tubulin Increases Cytoplasmic Dynein and Kinesin Processivity. Biophys J. 2000;78: 1955–1964. 10.1016/S0006-3495(00)76743-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Sirajuddin M, Rice LM, Vale RD. Regulation of microtubule motors by tubulin isotypes and post-translational modifications. Nat Cell Biol. 2014;16: 335–344. 10.1038/ncb2920 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Janke C, Chloë Bulinski J. Post-translational regulation of the microtubule cytoskeleton: mechanisms and functions. Nat Rev Mol Cell Biol. 2011;12: 773–786. 10.1038/nrm3227 [DOI] [PubMed] [Google Scholar]
  • 44.Luchko T, Torin Huzil J, Stepanova M, Tuszynski J. Conformational Analysis of the Carboxy-Terminal Tails of Human β-Tubulin Isotypes. Biophys J. 2008;94: 1971–1982. 10.1529/biophysj.107.115113 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.Mitchison T, Kirschner M. Dynamic instability of microtubule growth. Nature. 1984;312: 237–242. 10.1038/312237a0 [DOI] [PubMed] [Google Scholar]
  • 46.Nogales E, Whittaker M, Milligan RA, Downing KH. High-Resolution Model of the Microtubule. Cell. 1999;96: 79–88. 10.1016/S0092-8674(00)80961-7 [DOI] [PubMed] [Google Scholar]
  • 47.Ayoub AT, Craddock TJA, Klobukowski M, Tuszynski J. Analysis of the Strength of Interfacial Hydrogen Bonds between Tubulin Dimers Using Quantum Theory of Atoms in Molecules. Biophys J. 2014;107: 740–750. 10.1016/j.bpj.2014.05.047 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 48.Ayoub AT, Klobukowski M, Tuszynski JA. Detailed Per-residue Energetic Analysis Explains the Driving Force for Microtubule Disassembly. Briggs JM, editor. PLOS Comput Biol. 2015;11: e1004313 10.1371/journal.pcbi.1004313 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 49.Keskin O, Durell SR, Bahar I, Jernigan RL, Covell DG. Relating Molecular Flexibility to Function: A Case Study of Tubulin. Biophys J. 2002;83: 663–680. 10.1016/S0006-3495(02)75199-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 50.Gebremichael Y, Chu J-W, Voth GA. Intrinsic Bending and Structural Rearrangement of Tubulin Dimer: Molecular Dynamics Simulations and Coarse-Grained Analysis. Biophys J. 2008;95: 2487–2499. 10.1529/biophysj.108.129072 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 51.Pecqueur L, Duellberg C, Dreier B, Jiang Q, Wang C, Plückthun A, et al. A designed ankyrin repeat protein selected to bind to tubulin caps the microtubule plus end. Proc Natl Acad Sci. 2012;109: 12011–12016. 10.1073/pnas.1204129109 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 52.Nogales E, Wolf SG, Downing KH. Structure of the αβ tubulin dimer by electron crystallography. Nature. 1998;391: 199–203. 10.1038/34465 [DOI] [PubMed] [Google Scholar]
  • 53.Peng LX, Hsu MT, Bonomi M, Agard DA, Jacobson MP. The Free Energy Profile of Tubulin Straight-Bent Conformational Changes, with Implications for Microtubule Assembly and Drug Discovery. Alber MS, editor. PLoS Comput Biol. 2014;10: e1003464 10.1371/journal.pcbi.1003464 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 54.Isozaki N, Ando S, Nakahara T, Shintaku H, Kotera H, Meyhöfer E, et al. Control of microtubule trajectory within an electric field by altering surface charge density. Sci Rep. 2015;5 10.1038/srep07669 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 55.Xu Z, Schaedel L, Portran D, Aguilar A, Gaillard J, Marinkovich MP, et al. Microtubules acquire resistance from mechanical breakage through intralumenal acetylation. Science. 2017;356: 328–332. 10.1126/science.aai8764 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 56.Löwe J, Li H, Downing K., Nogales E. Refined structure of αβ-tubulin at 3.5 Å resolution 1 1Edited by I. A. Wilson. J Mol Biol. 2001;313: 1045–1057. 10.1006/jmbi.2001.5077 [DOI] [PubMed] [Google Scholar]
  • 57.Fiser A, Do RKG, Šali A. Modeling of loops in protein structures. Protein Sci. 2000;9: 1753–1773. 10.1110/ps.9.9.1753 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 58.Humphrey W, Dalke A, Schulten K. VMD: Visual molecular dynamics. J Mol Graph. 1996;14: 33–38. 10.1016/0263-7855(96)00018-5 [DOI] [PubMed] [Google Scholar]
  • 59.Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG. A smooth particle mesh Ewald method. J Chem Phys. 1995;103: 8577–8593. 10.1063/1.470117 [DOI] [Google Scholar]
  • 60.Huang J, MacKerell AD. CHARMM36 all-atom additive protein force field: Validation based on comparison to NMR data. J Comput Chem. 2013;34: 2135–2145. 10.1002/jcc.23354 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 61.Baker CM. Polarizable force fields for molecular dynamics simulations of biomolecules. Wiley Interdiscip Rev Comput Mol Sci. 2015;5: 241–254. 10.1002/wcms.1215 [DOI] [Google Scholar]
  • 62.Lemkul JA, Huang J, Roux B, MacKerell AD. An Empirical Polarizable Force Field Based on the Classical Drude Oscillator Model: Development History and Recent Applications. Chem Rev. 2016;116: 4983–5013. 10.1021/acs.chemrev.5b00505 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 63.Shi Y, Xia Z, Zhang J, Best R, Wu C, Ponder JW, et al. Polarizable Atomic Multipole-Based AMOEBA Force Field for Proteins. J Chem Theory Comput. 2013;9: 4046–4063. 10.1021/ct4003702 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 64.Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, et al. Scalable molecular dynamics with NAMD. J Comput Chem. 2005;26: 1781–1802. 10.1002/jcc.20289 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 65.Solomentsev GY, English NJ, Mooney DA. Hydrogen bond perturbation in hen egg white lysozyme by external electromagnetic fields: A nonequilibrium molecular dynamics study. J Chem Phys. 2010;133: 235102 10.1063/1.3518975 [DOI] [PubMed] [Google Scholar]
  • 66.Garate J-A, English NJ, MacElroy JMD. Human aquaporin 4 gating dynamics in dc and ac electric fields: A molecular dynamics study. J Chem Phys. 2011;134: 055110 10.1063/1.3529428 [DOI] [PubMed] [Google Scholar]
  • 67.Hekstra DR, White KI, Socolich MA, Henning RW, Šrajer V, Ranganathan R. Electric-field-stimulated protein mechanics. Nature. 2016;540: 400–405. 10.1038/nature20571 [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

S1 Fig. Secondary residue classifications in a 750 kV/cm EEF.

(A, B) The total number of residues that are classified as alpha helices or beta sheets during the application of 750 kV/cm EEFs of four directions: positive transverse, negative transverse, positive longitudinal, and negative longitudinal.

(TIFF)

Click here for additional data file. (6.6MB, tiff)
S2 Fig. Final displacement in a transverse external electric field and RMSF.

Final displacement, measured as the distance between residues after 10 ns exposure to a positive and negative transverse EEF (black). Cα RMSF per residue of a tubulin heterodimer, from the 10 to 20 ns time frame, without exposure to an EEF (blue).

(TIFF)

Click here for additional data file. (3.3MB, tiff)
S3 Fig. Salt bridges between the C-termini and the dimer surface.

Representative salt bridges experienced by the C-termini when in a contracted state (lying along the dimer’s surface). A distance cutoff of 3.2 Å and the positions of the initial frame, after equilibration, were used to identify possible salt bridges.

(TIFF)

Click here for additional data file. (3.6MB, tiff)
S4 Fig. Visualization of change in per-residue RMSF.

Same as Fig 4 but with ΔRMSF of each residue mapped onto the structure. Red and blue indicate an increase and decrease in RMSF, respectively. Field directions are indicated with arrows.

(TIFF)

Click here for additional data file. (5.7MB, tiff)
S5 Fig. Mean standard displacement of tubulin in a transverse external electric field.

Mean standard displacement (Å2) of tubulin from the start to the end of the application of a transverse EEF.

(TIFF)

Click here for additional data file. (3.5MB, tiff)

Data Availability Statement

The code used for analysis is available on Github at: https://github.com/JJTimmons/tubulin-in-an-EEF. Data is also available on FigShare at (DOI: https://figshare.com/s/32bd5a62009f184ebd47)

Articles from PLoS ONE are provided here courtesy of PLOS

RESOURCES