Table 1.

Definition and Calculation of Total (whole-molecule) and Local (Atom) Linear Indices of the Molecular Pseudograph’s Atom Adjacency Matrix of the 2-Aminobenzaldehyde Molecule.

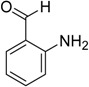2-Amino-benzaldehyde MolecularStructure		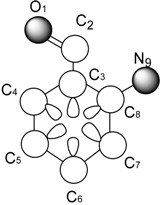Molecular Pseudograph (G) (hydrogen suppressed-pseudograph)			X = [O1, C2, C3, C4, C5, C6, C7, C8, N9] Molecular Vector: X∈ℜ9 In the definition of the X, as molecular vector, the chemical symbol of the element is used to indicate the corresponding electronegativity value. That is: if we write O it means χ(O), oxygen Mulliken electronegativity or some atomic property, which characterizes each atom in the molecule. Therefore, if we use the canonical basis of 9, the coordinates of any vector X coincide with the components of that molecular vector [X] = [3.17, 2.63, 2.63, 2.63, 2.63, 2.63, 2.63, 2.63, 2.33] [X]: column vector of coordinates of X in the Canonical base of R9 (a nx1 matrix)
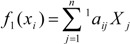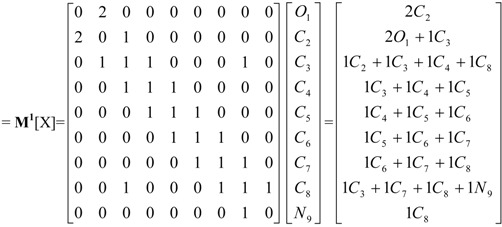
Atom linear indices of first order is a linear map; f1(xi): ℜn→ ℜn such that, f1(O1, C2, C3, C4, C5, C6, C7, C8, N9) = (2C2, 2O1+1C3, 1C2 +1C3+1C4+1C8, 1C3+1C4+1C5, 1C4+1C5+1C6, 1C5+1C6+1C7, 1C6+1C7+1C8, 1C3+1C7+1C8+1N9, 1C8) = (5.26, 8.97, 10.52, 7.89, 7.89, 7.89, 7.89, 10.22, 2.63) and whole-molecule linear indices of first order is a linear functional; 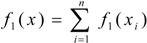=f1(O1) + f1(C2) + f1(C3) + f1(C4) + f1(C5) + f1(C6) + f1(C7) + f1(C8) + f1(N9)= 69.16
Local and total linear indices of order 0-5 (k = 0-5)
Atom (i)	f0(xi)		f1(xi)	f2(xi)		f3(xi)	f4(xi)	f5(xi)
O1	3.17		5.26	17.94		42.08	146.96	400.72
C2	2.63		8.97	21.04		73.48	200.36	676.25
C3	2.63		10.52	37.6		116.2	382.33	1193.57
C4	2.63		7.89	26.3		87.57	277.41	894.29
C5	2.63		7.89	23.67		73.64	234.55	739.87
C6	2.63		7.89	23.67		73.34	227.91	721.81
C7	2.63		7.89	26		80.93	259.35	820.73
C8	2.63		10.22	31.26		105.08	333.47	1080.23
N9	2.33		2.63	10.22		31.26	105.08	333.47
Total	23.91		69.16	217.7		683.58	2167.42	6860.94