A semiautomatic algorithm for three-dimensional segmentation of the prostate on CT images using shape and local texture characteristics

Abstract

Prostate segmentation in computed tomography (CT) images is useful for planning and guidance of the diagnostic and therapeutic procedures. However, the low soft-tissue contrast of CT images makes the manual prostate segmentation a time-consuming task with high inter-observer variation. We developed a semi-automatic, three-dimensional (3D) prostate segmentation algorithm using shape and texture analysis and have evaluated the method against manual reference segmentations. In a training data set we defined an inter-subject correspondence between surface points in the spherical coordinate system. We applied this correspondence to model the globular and smoothly curved shape of the prostate with 86, well-distributed surface points using a point distribution model that captures prostate shape variation. We also studied the local texture difference between prostate and non-prostate tissues close to the prostate surface. For segmentation, we used the learned shape and texture characteristics of the prostate in CT images and we used a set of user inputs for prostate localization. We trained our algorithm using 23 CT images and tested it on 10 images. We evaluated the results compared with those of two experts’ manual reference segmentations using different error metrics. The average measured Dice similarity coefficient (DSC) and mean absolute distance (MAD) were 88 ± 2% and 1.9 ± 0.5 mm, respectively. The averaged inter-expert difference measured on the same dataset was 91 ± 4% (DSC) and 1.3 ± 0.6 mm (MAD). With no prior intra-patient information, the proposed algorithm showed a fast, robust and accurate performance for 3D CT segmentation.

1. INTRODUCTION

Prostate cancer (PCa) is the most often diagnosed cancer among males in the United States, excluding skin cancer [1], and with more than 180,000 new cases diagnosed and more than 26,000 deaths in 2016 [1]. During last two decades, several image-guided procedures have developed for PCa diagnosis and therapy. Some of these procedures, e.g. radiation therapy, are performed with the prostate segmented on computed tomography (CT) images. However, due to low softtissue contrast, manual prostate segmentation on CT images is a time-consuming task with high intra- and inter-observer variability [2].

Recently, several computer-assisted segmentation algorithms have been developed to segment the prostate more quickly and with higher repeatability compared to manual segmentation [3–10]. A large majority of these algorithms were learning-based segmentation techniques that used previously segmented CT images from the same patient for training. In those cases, manual segmentation of previous CT images from the same patient must be available as a prerequisite for segmentation of the next image. On the other hand, all of the listed algorithms were evaluated against one set of manual reference and high inter-observer variability in manual segmentation was not taken into account for evaluation.

To address the need for a fast, accurate, and reproducible full 3D prostate segmentation on CT images and that is not related to intra-patient data for training and evaluated against multiple manual references, we present here a semiautomatic algorithm based on learned prostate shape variability and local image texture near the prostate border. The proposed technique does not need to be trained on previously acquired or manually segmented images from the target patient. We evaluated the performance of the algorithm against two manual references and compared the results to inter-expert observer variation.

2. METHODS

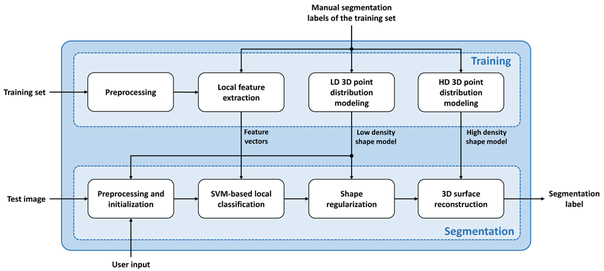
The proposed segmentation algorithm consists of two main steps: training and segmentation. For training the algorithm, we used an image set to i) extract a set of local texture features within each sector of the spherical space using the prostate centroid as the origin point and ii) model prostate shape with a low-density (LD) and a high-density (HD) point distribution model (PDM). During segmentation, the extracted texture features were used to train a set of classifiers and the shape models were used for shape regularization and surface reconstruction. Figure 1 shows a general block diagram of the method. Each of the blocks illustrated in this figure is described in detail below.

Figure 1.

General block diagram of the segmentation algorithm.

2.1. Training

Preprocessing:

First, we rotated each image about its inferior-superior axis in order to have the anteroposterior symmetry axis of the patient’s body aligned parallel to the anteroposterior axis of the image. We then truncated the Hounsfield unit (HU) range of the image by replacing values below −100 and above 155 with −100 and 155, respectively. This reduces the effect of non-soft tissue textures on our further measurements. A 3 × 3 2D median filter was then applied to each axial slice of the image to reduce the noise effect. Finally, the image and its manual segmentation label were resampled along the inferior-superior axis so as to have an isotropic voxel size for the image.

Shape modeling:

We defined two sets of 86 and 2056, equally spaced rays emanating from the prostate centroid and found their contact points with the prostate surface as surface landmarks. We used the landmarks to build two PDMs for prostate shape, i.e. one LD and one HD. To build the shape models we first aligned (rotated, scaled and translated) all the training segmentation labels using generalized Procrustes analysis [11] to minimize the least squares error between the landmarks. Then we applied principal component analysis to compute the eigenvalues and eigenvectors of the covariance matrix of the landmark coordinates. For more details see [12].

Local texture feature extraction:

We selected a set of points close to the prostate surface and on each of the 86 rays defined for shape modeling. For each point we defined a 3D cubic image patch centered at the point. For center points inside the prostate, the image patches were labeled as prostate patch and for center points outside the prostate the image patches were labeled as non-prostate patches. For each cubic image patch we calculated a set of 67 features consisting of:

• first-order features (including center voxel intensity, mean intensity, standard deviation of the intensities, median of the intensities, minimum intensity, maximum intensity, histogram skewness, histogram kurtosis, histogram entropy and histogram energy),

• eight-bin histogram of oriented gradients (HOG),

• eight-bin histogram of Local binary patterns (LBP),

• grey-level co-occurrence matrices (GLCM)-based features; i.e., energy, entropy, contrast, homogeneity, inverse different moment, correlation, cluster shade, and cluster prominence of GLCM, based on four, different 2D pixel neighboring, i.e. (−1,0), (0,−1), (1,−1), (−1,−1),

• eight-bin histogram of edge directions based on Sobel edge detection [13],

• and average of mean gradient angles of all 2D axial slices of the patch.

For details regarding feature calculation see [14-16], For each ray we selected the most discriminative feature set within the training set using the two-tailed t-test for each feature with the null hypothesis that the mean of the feature measured for prostate patches equals the mean of the feature measured for non-prostate patches. We used α=0.01 to reject the null hypothesis.

2.2. Segmentation

Preprocessing and initialization:

We used the similar preprocessing method (image alignment, HU truncation, and noise reduction) we applied to the training images for each test image. The segmentation algorithm required being initialized by an approximation of the prostate bounding box and 12 manually selected points on the prostate surface, termed anchor points, i.e. four points at four sides of an axial apex slice, four points at four sides of a mid-gland slice, and four points at four sides of a base slice. We estimated the centroid of the gland based on these inputs. We also used the bounding box and anchor points to extract the closest shape in the LD shape model that fits the input. This shape was considered as a rough initial surface estimation.

Local Classification:

We defined 86 rays emanating from the centroid, and for each ray we used the corresponding selected features to train a support vector machine (SVM) classifier for the ray. We used the classifier to classify the points on the ray close to the initial segmentation surface and selected a point on the ray as a candidate point for the prostate border. We repeated that for all the 86 rays in order to have a set of 86 candidate points for the prostate surface.

Shape regularization:

We fixed the selected surface points based on the manually selected anchor points and the bounding box, if required, and applied our LD shape model to find the closest shape in the model that fits the points in order to have a plausible shape for the prostate gland.

Surface reconstruction:

To reconstruct the prostate surface from the 86 points, we fitted the 86 corresponding points of our HD model to the 86 selected points and used the same transform function to transform all the 2056 points of the HD model shape. Then a scattered data interpolation was used to generate a continuous surface.

2.3. Evaluation metrics

We compared the results of the segmentation algorithm against manual segmentation using a set of segmentation error metrics including the Dice similarity coefficient (DSC), sensitivity (or recall) rate (SR), precision rate (PR), mean absolute distance (MAD), and volume difference (ΔV). MAD measures the disagreement between surfaces of two shapes. The MAD between two surfaces is the average of the shortest distances between each of the segmentation surface (S_s) points to the reference surface (S_ref points and defined as:

$$MAD(S_s,S_{ref})=\frac{1}{K}{\displaystyle \sum {}_{p\in S_s}{\min }_{q\in S_{ref}}}ED(p,q),$$ (1)

where, K is the number of points of S_s, p is a point in S_s, q is a point in S_ref, and ED(p, q) is the Euclidean distance between p and q. DSC, SR and PR are region-based error metrics that measures the overlap between two shapes. For 3D shapes, DSC is the ratio of the overlap volume to the average of the shape volumes:

$$DSC(V_s,V_{ref})=2\frac{V_s\cap V_{ref}}{V_s+V_{ref}}\times 100,$$ (2)

where, V_s and V_ref are algorithm segmentation and reference segmentation, respectively. SR is the ratio of the overlap volume to the volume of the reference:

$$SR(V_s,V_{ref})=\frac{V_s\cap V_{ref}}{V_{ref}}\times 100,$$ (3)

and PR is the ratio of the overlap volume to the volume of the algorithm segmentation:

$$PR(V_s,V_{ref})=\frac{V_s\cap V_{ref}}{V_s}\times 100.$$ (4)

The signed volume difference were defined as:

$$\Delta V(V_s,V_{ref})=V_s-V_{re\mathrm{f.}}$$ (5)

Here we reported ΔV values in cm³. The positive values of ΔV indicate over segmentation, and the negative values of ΔV indicate under-segmentation. For more details regarding the metric calculation see [17-19]

3. DATA AND EXPERIMENTS

3.1. Materials

The dataset used in this study contained 33 3D abdominal CT scans from 33 patients. Each image was 512 × 12 × 27 voxels in size with a voxel size of 0.977 × 0.977 × 4.25 mm³. For each image, two manual segmentations were provided by two expert radiologists.

3.2. Inter-observer variability

To quantify the inter-observer variation in manual segmentation, we compared our two manual references to each other using our segmentation error metrics. For MAD calculation, we measured two MAD values for each case; one when the first manual segmentation label is used as the reference and the other when the second manual segmentation label is considered as the reference. We used the average of the two MAD values, called bilateral MAD (MAD_b), to measure surface disagreement between two manual segmentation labels. For ΔV measurement, we calculate the absolute value of the volume difference (|ΔV|).

3.3. Accuracy measurements

To measure the accuracy of the algorithm, we randomly chose 70% of the images (23 images) to train and the rest 30% of the images (10 images) to test the algorithm. We applied the proposed algorithm to segment the 10 test images using reference segmentation #1 for initialization of the algorithm. For each test image, we defined the bounding box and the 12 anchor points based on the manual segmentation label. To evaluate the segmentation results we compared the algorithm segmentation label to the same reference used for initialization of the algorithm (i.e., reference #1) using our segmentation error metrics.

3.4. Two-operator test accuracy measurements

To measure the impact of different operators’ input on the algorithm performance, we run the algorithm with the similar configuration used for accuracy measurement in subsection 3.3, but we used two different sets of operator inputs for initialization of the algorithm. To evaluate the results, we compared each set of results to the reference segmentation labels from the corresponding operator. We compared the average segmentation errors with each other and to the average difference between the two manual references using DSC and MAD error metrics.

3.5. Segmentation time

We developed a parallel implementation of the segmentation algorithm on Matlab platform using parallel computing toolbox. We run the code on 12 CPU cores on a 64-bit computer with Windows 7 operating system, 3.0 GHz Intel Xeon processor and 64 GB of memory. The total segmentation time includes operator interaction time for initializing the algorithm (i.e., selecting the bounding box and the 12 anchor points) and the algorithm execution time. We recorded the manual operator interaction time and algorithm execution time separately. The operator interaction time for initialization of the algorithm was recorded based on the inputs by a research scholar with experience in reading prostate CT images.

4. RESULTS

4.1. Inter-observer variation

The measured average ± standard deviation (range) for the whole gland based on DSC, MAD_b, and ΔV were 91 ± 4% ([85%, 96%]), 1.3 ± 0.6 mm ([0.6 mm, 2.7 mm]), and 4.2 ± 7.0 cm³ ([0.3 cm³, 23.9 cm³]), respectively. Table 1 shows the results for different regions of interest (ROIs). These results show slightly better agreement between the two experts for manual segmentation of mid-gland and base of the prostate compare to apex.

Table 1.

The disagreement between two expert observers in manual segmentation of the prostate in CT images.

Region of Interest	Npat	NImg	MADb (mm)	DSC (%)	|ΔV| (cm3)
Whole Gland	10	10	1.3 ± 0.6	91 ± 4	4.2 ± 7.0
Apex			1.4 ± 0.7	88 ± 7	1.5 ± 2.4
Mid-Gland			1.3 ± 0.8	93 ± 4	2.1 ± 3.1
Base			1.2 ± 0.5	93 ± 3	1.3 ± 1.4

4.2. Accuracy measurements

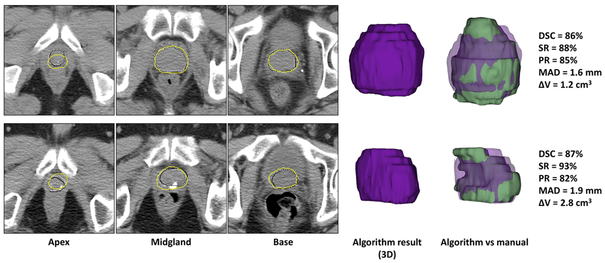
Table 2 shows the accuracy of the algorithm compared to a single manual reference and compares them to a group of recently published segmentation algorithms. Figure 2 shows the segmentation results for two, sample cases.

Table 2.

The accuracy of the proposed algorithm against the manual reference compared to a number of recently published methods. The significant differences detected between the metric values of the other method and the corresponding metric values of our methods are shown in bold (p < 0.05).

Method, Year	NPat	NImg	MAD (mm)	DSC (%)	SR (%)	PR (%)	Execution Time (second)
Proposed algorithm	10	10	1.9 ± 0.5	88 ± 2	94 ± 3	82 ± 4	22 ± 2
Ma et al. [9], 2017	92	92	-	87 ± 3	87 ± 5	-	11
Ma et al.[8], 2016	15	15	-	85 ± 3	83 ± 1	-	-
Shi et al. [20], 2016	24	330	1.3 ± 0.8	92 ± 4	90 ± 5	-	-
Shi et al. [6], 2015	24	330	1.1 ± 0.6	95 ± 3	93 ± 4	-	-
Shao et al.[5], 2015	70	70	1.9 ± 0.2	88 ± 2	84	86	-
Shi et al. [4], 2013	24	330	1.1	94 ± 3	92 ± 4	-	-
Liao et al.[3], 2013	24	330	1.0	91	-†	-	156

Figure 2.

Qualitative and quantitative segmentation results for two, sample cases. Each row shows the results for one patient. For each image, the algorithm segmentation results are shown with yellow contours and the reference contours with solid black contours (first reference) and dotted white contours (second reference) on three, sample 2D slices. The 3D segmentation results (purple volumes) are also shown and compared to the first references (green volumes).

4.3. Two-operator test accuracy measurements

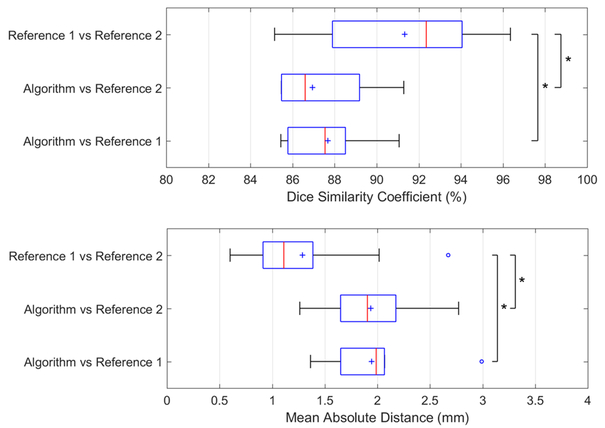
Figure 3 compares the algorithm performance based on MAD and DSC error metrics when two different sets of manual reference segmentation labels were used for initialization of the algorithm. We used the box plots to compare the average segmentation errors with each other and to the average difference between two manual references.

Figure 3.

Segmentation algorithm’s performance based on two operators and two references compared to inter-observer variability in manual segmentation. Box plots show the minimum (left bar), 25 percentile to 75 percentile (blue box), maximum (right bar), median (red line), and mean (blue cross symbol) values of DSC and MAD across 10 test images. The outliers are shown with blue ‘o’ symbols. The asterisk indicates statistically significant differences between the means (p < 0.05).

4.4. Segmentation time

The average operator interaction time for the test image set was 53 ± 9 seconds per 3D image. This time includes selecting a bounding box and 12 anchor points on the prostate boundary. The average measured execution time for 3D segmentation of each test image was 22 ± 2 seconds.

5. DISCUSSION AND CONCLUSIONS

We developed and evaluated a semi-automatic, learning-based algorithm for full 3D segmentation of the prostate on CT images. The proposed segmentation technique does not need to be trained on previously acquired or manually segmented images of the same patient. We trained the algorithm based on learned local texture and shape characteristics of the prostate in a training CT image dataset. A set of ray-specific, trained SVMs were used for segmentation of an unseen prostate CT image. We evaluated the performance of our algorithm against two, different manual references and compared the results with inter-observer variation in manual segmentation. The evaluation results show that the proposed method could achieve a segmentation accuracy close to the observed variation between manual references (< 5% and < 0.7 mm in terms of DSC and MAD, respectively). The results are comparable to the previously published work in the literature with a higher average sensitivity rate. The average 3D segmentation time, including the manual operator interaction time, is 75 seconds per image which is more than three times lower than manual prostate segmentation time reported in [21]. Since the presented technique is not related to previously acquired, and/or segmented CT images from the same target patient, it could be used for radiation therapy planning CT image segmentation. Our future work will focus on testing the algorithm on a larger dataset and evaluating the performance of the algorithm on a radiation therapy planning performance.