Fig. 3.

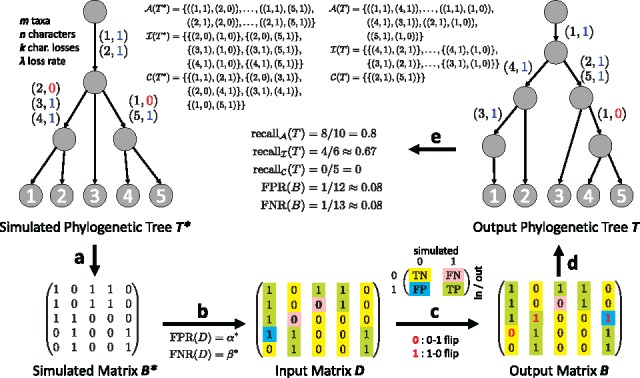
Simulation setup and comparison measures. (a) Given the number m of taxa and n of characters, we use the ms package (Hudson, 2002) to simulate a perfect phylogeny tree. Subsequently, we introduce at most k losses per character using a rate λ, yielding the simulated phylogenetic tree $T^{*}$ and matrix $B^{*}$. (b) We then perturb the entries of $B^{*}=[b_{p,c}^{*}]$ given a false positive rate $\text{FPR}(D)={\alpha }^{*}$ and false negative rate $\text{FPNR}(D)={\beta }^{*}$, yielding the input matrix $D=[d_{p,c}]$. Entry $d_{p,c}=0$ is a true negative (TN) if $b_{p,c}^{*}=0$ and a false negative (FN) if $b_{p,c}^{*}=1$. Conversely, $d_{p,c}=1$ is a false positive (FP) if $b_{p,c}^{*}=0$ and a true positive (TP) if $b_{p,c}^{*}=1$. (c) Given D, ${\alpha }^{*}$ and ${\beta }^{*}$, a phylogeny estimation method yields output matrix $B=[b_{p,c}]$. (d) In addition, such a method outputs a phylogenetic tree T whose leaves form the rows of output matrix B. (e) To compare T and $T^{*}$, we compute the recall in terms of pairs of character states that are ancestral ($\mathcal{A}$), on distinct branches (incomparable, $\mathcal{I}$), or on the same edge (clustered, $\text{C}$). A recall of 1 for all three measures implies that (the internal nodes of) T and $T^{*}$ are identical. To compare B and $B^{*}$, we compute $\text{FPR}(B)$ and $\text{FNR}(B)$—if both are 0 then $B=B^{*}$