Deep longitudinal transfer learning-based automatic segmentation of photoreceptor ellipsoid zone defects on optical coherence tomography images of macular telangiectasia type 2

Abstract

Photoreceptor ellipsoid zone (EZ) defects visible on optical coherence tomography (OCT) are important imaging biomarkers for the onset and progression of macular diseases. As such, accurate quantification of EZ defects is paramount to monitor disease progression and treatment efficacy over time. We developed and trained a novel deep learning-based method called Deep OCT Atrophy Detection (DOCTAD) to automatically segment EZ defect areas by classifying 3-dimensional A-scan clusters as normal or defective. Furthermore, we introduce a longitudinal transfer learning paradigm in which the algorithm learns from segmentation errors on images obtained at one time point to segment subsequent images with higher accuracy. We evaluated the performance of this method on 134 eyes of 67 subjects enrolled in a clinical trial of a novel macular telangiectasia type 2 (MacTel2) therapeutic agent. Our method compared favorably to other deep learning-based and non-deep learning-based methods in matching expert manual segmentations. To the best of our knowledge, this is the first automatic segmentation method developed for EZ defects on OCT images of MacTel2.

1. Introduction

Macular telangiectasia type 2 (MacTel2) is a progressive retinal disease of unknown cause which affects with varying severity the juxtafoveolar region of both eyes. Clinical signs of MacTel2 include loss of retinal transparency, crystalline deposits, telangiectatic vessels, and pigment plaques which result in a slow decline in visual acuity [1–5]. The early signs are often subtle and difficult to identify with ophthalmoscopy [3].

With optical coherence tomography (OCT) it is possible to obtain high-resolution retinal images [6], on which retinal layer boundaries can be delineated with micron (and even submicron [7]) accuracy. OCT has become a valuable tool to diagnose MacTel2 [2]. Signs of MacTel2 visible on OCT include hypo-reflective spaces in the inner and outer retina, thinning and defects of the retina temporal to the foveal center, and atrophy of the hyper-reflective layer or band that is located external to the external limiting membrane (ELM) and internal to a band thought to represent cone photoreceptor tips [2–5, 8, 9]. There is an ongoing lively debate regarding the exact cellular structure that correlates with this hyper-reflective band and the nomenclature used to describe it. Recent publications [10–16], including that from a consensus International Nomenclature group [17], refer to this band as the ellipsoid zone (EZ) as it is thought to represent the ellipsoid region of the photoreceptor inner segments which have densely-packed mitochondria that are likely hyper-reflective on OCT [18]. However, other studies, including a recent one that used adaptive optics to characterize this structure [9], refer to it as the junction between the inner segments and outer segments (IS/OS) of the photoreceptors [2–4, 8, 19–22]. In this paper, without making a judgment about the true nature of this band, we have used the EZ terminology, as it is more commonly used in the recent MacTel2 clinical trial literature [13, 23–25].

The 3-dimensional (3-D) information contained within OCT images can be projected to create a 2-D en face summed voxel projection (SVP) image. The SVP is useful to assess topographic locations and to quantify retinal lesion areas that include those caused by EZ atrophy or defects [2–4, 23].

Correlation between EZ defects and loss of retinal function has been established in previous MacTel2 studies [3, 4, 19, 20, 23, 26], in which segmentation of EZ defects has been achieved manually [3,4] or semi-automatically [21, 23]. Of note, the semi-automatic method by Mukherjee et al. [23] used a popular graph search algorithm [27, 28] to automatically segment retinal layer boundaries on individual OCT B-scans, which were then assessed and manually corrected by expert graders. An en face thickness map was generated from these segmentations, and thresholded to determine EZ defect areas. Subsequently, Gattani et al. [21] developed an iterative semi-automatic method to segment EZ defect boundaries based on manual initialization of seed locations by the user on the en face image.

EZ defects are also observed in other retinal diseases such as age-related macular degeneration (AMD) [22], macular edema (ME) [10], and diabetic retinopathy (DR) [11]. Semi-automatic EZ defects analysis has also been performed in these diseases [10, 12, 29].

Automatic segmentation and quantification of EZ defects would be a very useful tool to analyze EZ defects in clinical trials, especially in longitudinal studies where patients are observed over time to monitor disease progression or treatment efficacy. Most recently, Wang et al. [11] developed an automatic method to detect EZ defects in OCT images of DR using graph search and fuzzy c-means. In general, these automatic and semi-automatic methods to segment EZ defects involve a two-step process; first, defective retinal layer boundaries are segmented (e.g. using graph search [30–32], random forest classifiers [33], or active contours [34]); then, EZ thicknesses or pixel intensities are projected onto an en face image where EZ defects can be identified.

Deep learning is a powerful approach that has been used, especially in the past few years, in computer vision for object recognition, classification, and semantic segmentation [35–40]. Deep learning methods have been successfully used in many areas of medical imaging; for example, to detect and classify lesions, to segment organs and sub-structures, and to register and enhance medical images [41]. Convolutional neural networks (CNNs) are particularly suitable for image analysis. A CNN generally consists of several layers of filters learned from labeled training data that extract multi-scale features from an input and then map the extracted features to the associated label. Deep learning models have also been applied to a variety of ophthalmic image processing applications [42–47] that include OCT layer segmentation algorithms. Specifically, Fang et al. [48] was the first to utilize a CNN to segment inner retinal layer boundaries on OCT images of diseased eyes. Roy et al. [49], Xu et al. [50], and Venhuizen et al. [51] adopted variant versions of the fully-convolutional network (FCN) [37] and U-net [52] CNN models to delineate the boundaries of fluid masses and pigment epithelium detachment. Many other variants of CNNs have been recently employed for segmenting a variety of anatomic and pathologic features on OCT images [53–59].

Quantification of targeted biomarkers assessed at different time points (e.g. the growth of EZ defect areas over time) is a key method to evaluate treatment efficacy in clinical trials, as well as in clinical care. As such, patients enrolled in a clinical trial are frequently imaged with OCT over multiple visits. The accuracy of classic automatic image segmentation techniques (e.g. graph search [27]) is similar for all these visits, and at each visit, segmentation errors must be manually corrected [60–62]. Accordingly, the overall human workload to manually correct these errors is relatively constant at each visit using these classic techniques. However, despite progression of disease and treatment effects, it is reasonable to assume that the OCT images from the same eye of the same patient at different visits should have strong similarities in their anatomical and pathological structures. Fortunately, deep learning frameworks are well-suited to analyze temporal data, such as electronic medical health records [63–65]. For medical images, we will show how the algorithm can learn from its errors in previous encounters with images of a specific subject, which can, thereby, decrease the need for manual correction at each visit.

In this paper, we describe a novel deep learning-based method using a CNN to automatically segment 2-D en face EZ defect areas from 3-D OCT volumes obtained from eyes with MacTel2 without the need to segment retinal layer boundaries as an intermediate step. We further developed a transfer learning paradigm to learn from mistakes in segmenting the baseline images of a particular subject and fine-tuned our CNN to segment with higher accuracy the subsequent OCT images. We show the efficacy of our deep learning-based method with longitudinal transfer learning, which we call Deep OCT Atrophy Detection (DOCTAD), to segment images obtained from a clinical trial of a novel therapeutic agent to inhibit the progression of EZ defects in eyes with MacTel2.

2. Methods

We developed and trained DOCTAD to classify the EZ on individual OCT A-scans as normal or defective (atrophied) and automatically estimate the EZ defect areas in OCT volumes. In addition, a transfer learning procedure was utilized to demonstrate the benefits of learning from a subject’s past scan information to improve the segmentation at future time points. The performance of DOCTAD was evaluated using the Dice similarity coefficient and errors in the predicted EZ defect areas.

2.1 Data set

The study data set consisted of retinal spectral domain (SD)-OCT volumes of 134 eyes from 67 subjects from the international, multicenter, randomized phase 2 trial of ciliary neurotrophic factor for MacTel2 (NCT01949324; NTMT02; Neurotech, Cumberland, RI, USA). This study complied with the Health Insurance Portability and Accountability Act (HIPAA) and Clinical Trials (United States and Australia) guidelines, adhered to the tenets of the Declaration of Helsinki and was approved by the institutional ethics committees at each participating center.

We analyzed data at two different time points, six months apart, at which subjects were imaged on Spectralis SD-OCT units (Heidelberg Engineering GmBH, Heidelberg, Germany) at different imaging centers. We refer to the SD-OCT volumes obtained at the first time point as the baseline volumes and those obtained at the second time point as the 6-month volumes. The data set consisted of a total of 25,876 B-scans. Most SD-OCT volumes consisted of 97 B-scans with 1024 A-scans each, within a 20° × 20° (approximately 6 mm × 6 mm) retinal area. The exceptions were two 6-month volumes with 37 B-scans, and twelve baseline and four 6-month volumes with 512 A-scans per B-scan. All B-scans had a height of 496 pixels with an axial pixel pitch of 3.87µm/pixel. We removed no subject or eye from the data set regardless of image quality or defect size, and even included those eyes that were eventually excluded from the clinical trial, to be most faithful to a real-world clinical trial scenario, whereby the segmentation outcome determines the eligibility for trial enrollment.

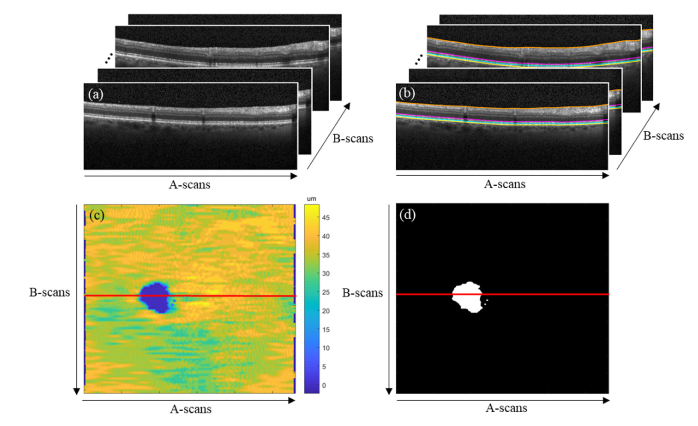
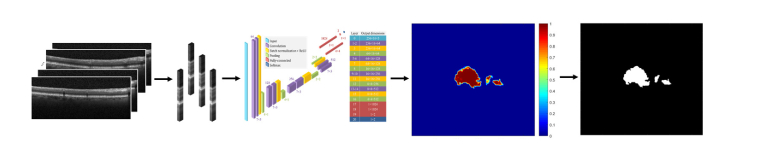
The process to attain the gold standard EZ defects segmentation is described in our previous publication [23]. In brief, for each B-scan, the inner limiting membrane (ILM), inner EZ, inner retinal pigment epithelium (RPE), and Bruch’s membrane (BrM) layer boundaries were first segmented by graph search [27, 28] using the Duke OCT Retinal Analysis Program (DOCTRAP; Duke University, Durham, NC, USA) software. Automatic segmentation was reviewed and manually corrected by an expert Reader at the Duke Reading Center. A second, more senior Reader reviewed the layers delineated by the first Reader and corrected these segmentations, as needed. An EZ thickness map was generated by axially projecting the EZ thicknesses, defined by the inner EZ and inner RPE layer boundaries, onto a 2-D en face image. This image was then interpolated using bicubic interpolation to obtain a pixel pitch of 10µm in each direction. EZ thicknesses of less than 12µm were classified as EZ defects [23] and the EZ thickness map was thresholded to obtain a binary map of EZ defects. The resulting binary map of EZ defects was used as the gold standard in this study. Figure 1 illustrates this process and Fig. 2 shows a representative B-scan with EZ defects.

Fig. 1.

(a) Retinal OCT volume. (b) Gold standard (manual) segmentation of the ILM (orange), inner EZ (magenta), inner RPE (cyan), and BrM (yellow) layer boundaries by expert Readers. The EZ thickness is defined by the inner EZ and inner RPE layer boundaries. (c) En face EZ thickness map. (d) Gold standard (manual) binary map of EZ defects. EZ thicknesses of less than 12µm were classified as EZ defects.

Fig. 2.

B-scan from the position marked by the red line on Fig. 1(c-d) showing the gold standard (manual) segmentation of the inner EZ (magenta) and inner RPE (cyan) layer boundaries by expert Readers and the EZ defects identified (white).

2.2 Cluster extraction

Since EZ defects are usually continuous in a local region, it is natural to assume that information from adjacent A-scans and B-scans can be useful in determining the absence or presence of EZ defects. Thus, the training of DOCTAD was based on a set of normal and defective A-scan clusters which were sampled from the OCT volumes as follows.

As a pre-processing step, we first used a simple method to swiftly locate an approximated location of the retina in the OCT volume and to remove as much of the background as possible while retaining full view of the retina. For each volume, the 20th B-scan was smoothed with a Gaussian filter (11 × 11 pixels, σ = 11 pixels) and thresholded (at 0.4 of the maximum intensity of the smoothed image) to obtain estimates of the retinal nerve fiber layer (RNFL), the innermost retinal layer, and the RPE layer, which is just external to the outer retinal boundary. These layers often appear as the brightest layers in the image. For each A-scan, the mean position of the RNFL and RPE was calculated and the median value across all A-scans was taken to be the estimated center of the retina for the volume. Then, all the images in the volume were cropped to a height of 256 pixels about the estimated center.

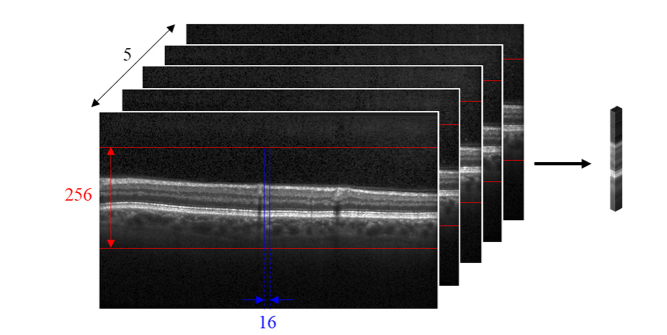
For every A-scan, a cluster of A-scans (256 × 16 × 5 pixels) centered at that A-scan was extracted and labeled according to the gold standard manual segmentation. Any clusters that fell outside the lateral field-of-view were mirrored about the center A-scan. Figure 3 illustrates the dimensions of such a cluster. We used data from a carefully-designed clinical trial. Nonetheless, some of the volumes had different scan densities. Accordingly, to ensure that our algorithm was robust, even given image acquisition inconsistencies that resulted in volumes with varying scan densities, we used the same cluster dimensions for all volumes to train the CNN to be invariant to scan density. Additionally, efficient CNNs for classification are often trained with approximately equal numbers of samples per class. Thus, since the EZ defect areas in the volumes were very small compared to the normal EZ areas, for each volume, normal clusters were randomly sampled with a probability equal to the ratio between the EZ defect area and normal area.

Fig. 3.

Clusters of dimensions 256 × 16 × 5 pixels were extracted from the OCT volumes.

2.3 CNN architecture

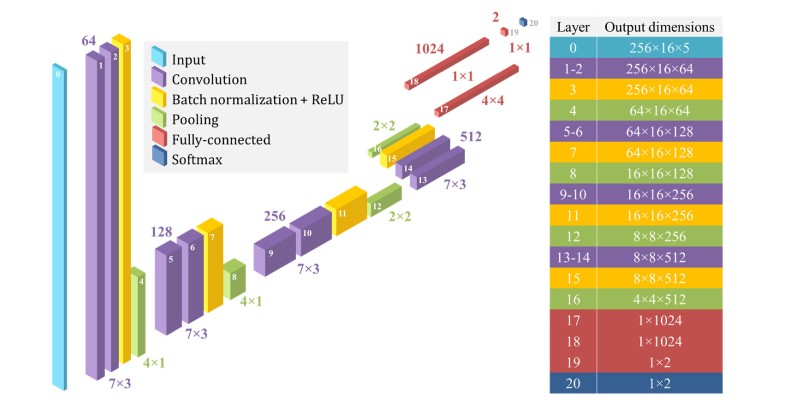
The CNN architecture used in DOCTAD is shown in Fig. 4. It consists of 20 convolutional, pooling, batch normalization, fully-connected, and softmax layers. It was constructed using standard CNN design principles. Certain aspects were modified to suit the structure of our data. In the convolutional layers, rectangular (7 × 3 pixels) instead of square (3 × 3 pixels) filters were used to extract features as the retinal images have greater variation in the vertical direction. A batch normalization layer, which has been demonstrated to improve training [66], was added after the convolutional layers before the rectified linear unit (ReLU) operation was applied. In the first two pooling layers, we used 4 × 1 max-pooling instead of the conventional 2 × 2 max-pooling to efficiently downsample the input as it propagated through the network. At the end of the network is a softmax layer to perform classification. In this case, our architecture performed binary classification (normal or defective) and the final output was a two-element vector.

Fig. 4.

DOCTAD CNN architecture showing the number of features (top) and filter sizes (bottom) of the convolutional and fully-connected layers, pooling sizes of the pooling layers, and the output dimensions of each layer as indicated by the layer number.

2.4 Training the CNN

The CNN was trained on the clusters and labels extracted from the baseline volumes of subjects in the training set. The parameters of the CNN were randomly initialized using Xavier initialization [67] and optimized using Adam optimization [68] to minimize the binary cross-entropy loss, $\mathcal{L}$ defined as

$$\mathcal{L}=-\frac{1}{N}{\displaystyle \sum _{i=1}^N[y_i\log (p_i)+(1-y_i)\log (1-p_i)}]$$ (1)

where y_i is the gold standard class label (0 for normal, 1 for defective) and p_i is the predicted probability of the cluster i being defective. N is the number of clusters used per mini-batch or the mini-batch size. The value of p_i was the final output from the softmax layer. A mini-batch size of 250 and learning rate of 0.0001 was used during training, without any weight regularization. The network was trained for a maximum of 10 epochs until the best performance was achieved on a hold-out validation set, which was usually between 3 to 10 epochs in our experiments. Performance metrics are detailed in Section 2.7.

2.5 Prediction

Once trained, DOCTAD was used to predict a binary map of EZ defects from a given OCT volume of an eye. During prediction, clusters centered on every A-scan were extracted and passed as inputs to the trained CNN to obtain the probability of each cluster being defective. An en face probability map was generated and interpolated to obtain a pixel pitch of 10µm in each direction. Any clusters with a probability of greater than 0.5 was considered defective and the probability map was thresholded to obtain the final predicted binary map of EZ defects. Figure 5 illustrates this process.

Fig. 5.

During prediction, clusters of every A-scan were extracted from the given OCT volume and passed as inputs to the trained CNN to generate an en face probability map which was thresholded to obtain the predicted binary map of EZ defects.

2.6 Longitudinal transfer learning

As previously mentioned, deep learning frameworks are well-suited to take advantage of the correlation between the OCT images from the same eye of the same patient at different time points. Thus, we expect that fine-tuning a trained CNN on a specific subject’s scan information from a previous time point would improve its performance when making a prediction on the same subject’s scans at a future time point.

In this sub-section, we utilize an interpretation of the general transfer learning approach [69], which we call longitudinal transfer learning. In longitudinal transfer learning, we fine-tune the proposed CNN model based on the semi-automatically corrected segmentations acquired at a previous time point and use the fine-tuned model to automatically segment the EZ defects in the same eye at a later time point. Specifically, we first train the CNN as described in Section 2.4 with the baseline volumes. Then, for each eye in our data set, we fine-tuned the trained CNN with clusters extracted from the baseline volume and evaluated performance on the 6-month volume of the corresponding eye. To fine-tune the CNN, we used a smaller batch-size of 100, lowered the learning rate to 0.00001, and trained it for a maximum of 10 epochs until the best performance was achieved on the baseline volume. It is possible that fine-tuning does not improve the performance on the baseline volume of some subjects. In these cases, the CNN is not updated and the performance both before and after fine-tuning would be unchanged.

2.7 Performance metrics

Two metrics were used to evaluate the performance of DOCTAD – the Dice similarity coefficient (DSC) [70] and errors in the predicted EZ defect areas.

The DSC was calculated between the gold standard and predicted binary map of EZ defects as

$$DSC=\frac{2TP}{2TP+FP+FN},$$ (2)

where TP was the number of true positives, FP was the number of false positives and FN was the number of false negatives (in pixels) in the predicted binary map of EZ defects. False positives or “over-prediction” indicated a scenario in which DOCTAD predicted EZ defects where the gold standard identified the area as normal. False negatives or “under-prediction” indicated a scenario in which DOCTAD failed to predict EZ defects where the gold standard identified the area as defective. The DSC ranged from 0 to 1 where a value of 1 indicated complete agreement between the gold standard and predicted binary maps of EZ defects. This metric was the one used to monitor the performance on the hold-out validation set during training.

The DSC is a relative measure and for volumes with small EZ defect areas, the DSC is drastically affected by small errors. In the extreme case, for example, a volume with no EZ defects will have a DSC of 0 if even one pixel is predicted as defective. Thus, we also calculated the total, E_t and net, E_n errors of the predicted EZ defect areas as

$$E_t=k\left|FP+FN\right|,$$ (3)

$$E_n=k\left|FP-FN\right|,$$ (4)

where k = 0.0001 is the conversion factor from pixels to mm² and $|.|$ is the absolute value. The errors in the predicted EZ defect areas are absolute values and this metric is, therefore, more robust, especially for volumes with small EZ defect areas.

2.8 Implementation

DOCTAD was implemented in Python using the TensorFlow [71] (Version 1.2.1) library. On a desktop computer equipped with an Intel Core i7-6850K CPU and four NVIDIA GeForce GTX 1080Ti GPUs, the average prediction time was approximately 12 seconds per SD-OCT volume. For longitudinal transfer learning, the average deployment time to fine-tune the CNN was approximately 5 minutes per SD-OCT volume.

3. Results

We report the average performance metrics of DOCTAD and alternative methods on all volumes, as well as the subset of clinically-significant (CS) volumes. CS volumes were defined as volumes having a gold standard EZ defect area of more than 0.16 mm², consistent with the lower limit EZ defect area required for enrollment in the MacTel2 clinical trial [23].

3.1 Comparison to alternative methods on baseline volumes

We compared DOCTAD to the alternative method whereby the layer boundaries were first segmented, and then the EZ thicknesses projected onto an en face image where EZ defects could be identified. To segment the layer boundaries, we used two popular retinal layer boundary segmentation algorithms – DOCTRAP [27, 28], a graph search-based algorithm, and CNN-GS [48], a deep learning-based algorithm. We compared the performance of DOCTAD to DOCTRAP and CNN-GS on the baseline volumes in our data set.

DOCTRAP automatically segments 9 layer boundaries. The inner EZ and inner RPE correspond to boundaries 7 and 8, respectively. To account for any biases due to different conventions in marking the boundaries, we calculated the pixel shift that minimized the absolute difference between the DOCTRAP boundary segmentations with respect to the gold standard boundary segmentation across all baseline volumes and found that no pixel shifts were necessary.

To train both CNN-GS and DOCTAD, we used 6-fold cross validation to ensure independence of the training and testing sets. The 67 subjects were divided into six folds (groups), each consisting of 11 or 12 subjects. Baseline volumes of the subjects in five folds were used as the training set while the remaining volumes were used as the testing set. From the training set, volumes of subjects in one fold were set aside as the hold-out validation set. In the original work, CNN-GS was trained to segment 9 layer boundaries. However, as our data set consisted of only 4 manually-segmented layer boundaries as shown in Fig. 1(b), we modified the CNN-GS architecture to predict only 4 layer boundaries and trained CNN-GS using the methodology and parameters as described in the original work [48]. We trained DOCTAD as described in Section 2.4.

For DOCTRAP and CNN-GS, an EZ thickness map was generated for each volume by axially projecting the EZ thicknesses onto an en face image and interpolating to obtain a pixel pitch of 10µm in each direction as in the gold standard. EZ thicknesses of less than 12µm were classified as EZ defects and the EZ thickness map was thresholded to obtain a predicted binary map of EZ defects. For DOCTAD, the predicted binary maps of EZ defects were directly obtained as described in Section 2.5. Table 1 shows the average performance metrics of DOCTRAP, CNN-GS, and DOCTAD on the baseline volumes.

Table 1. Performance metrics (mean ± standard deviation, median) of DOCTRAP [27, 28], CNN-GS [48], and our new DOCTAD method on 134 baseline volumes using 6-fold cross validation.

Volumes	Performance metric	Method
		Gold standard (Manual)	DOCTRAP	CNN-GS	DOCTAD
All	EZ defect areas (mm2)	0.68 ± 0.69, 0.51	0.03 ± 0.04, 0.01	0.32 ± 0.40, 0.19	0.71 ± 0.66, 0.55
	DSC	-	0.06 ± 0.15, 0.02	0.50 ± 0.23, 0.53	0.79 ± 0.22, 0.87
	Et (mm2)	-	0.67 ± 0.68, 0.52	0.46 ± 0.51, 0.32	0.19 ± 0.21, 0.13
	En (mm2)	-	0.66 ± 0.67, 0.49	0.40 ± 0.44, 0.28	0.11 ± 0.17, 0.06
CS	EZ defect areas (mm2)	0.84 ± 0.68, 0.67	0.03 ± 0.05, 0.01	0.39 ± 0.41, 0.25	0.87 ± 0.64, 0.71
	DSC	-	0.05 ± 0.06, 0.03	0.52 ± 0.18, 0.54	0.86 ± 0.12, 0.89
	Et (mm2)	-	0.83 ± 0.68, 0.63	0.56 ± 0.52, 0.38	0.22 ± 0.22, 0.15
	En (mm2)	-	0.81 ± 0.67, 0.62	0.49 ± 0.44, 0.33	0.12 ± 0.18, 0.07

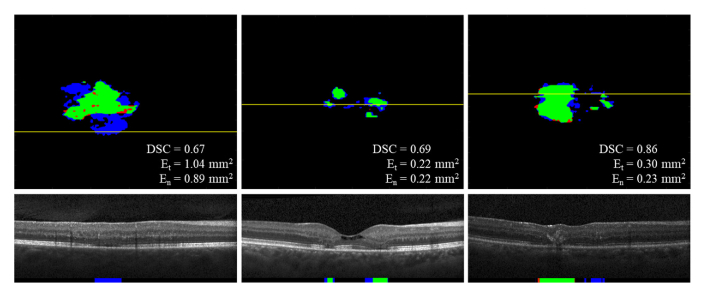
The overall performance of both DOCTRAP and CNN-GS were poor with small DSC values and large errors. DOCTAD was able to identify EZ defects areas with high accuracy, resulting in a mean DSC of 0.86 on 107 CS volumes. Figures 6–7 show examples of the boundary segmentations and predicted EZ defect areas by DOCTRAP, CNN-GS, and DOCTAD. The errors made by DOCTAD occurred mostly around the boundaries of the EZ defect areas, some of which are difficult to classify even for expert Readers, as further discussed in Section 3.3.

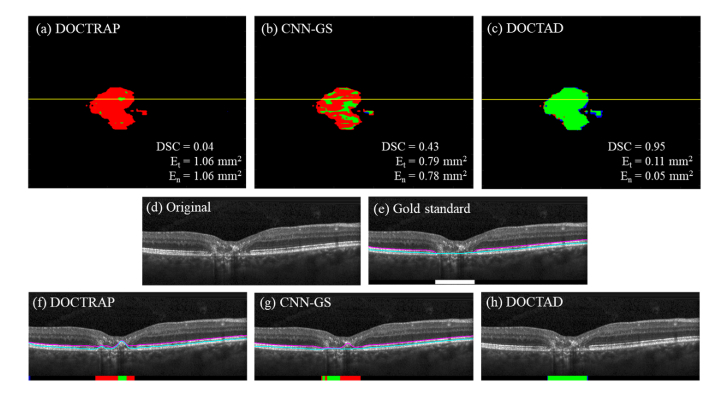
Fig. 6.

(a – c) Overlay of gold standard (manual) and predicted binary maps of EZ defects by DOCTRAP, CNN-GS, and our new DOCTAD method showing TP (green), FP (blue) and FN (red). (d) B-scan from the position marked by the yellow line on (a-c). (e) Gold standard (manual) boundary segmentations and EZ defect areas (white). (f – h) Boundary segmentations and predicted EZ defect areas by DOCTRAP, CNN-GS, and DOCTAD showing TP (green), FP (blue) and FN (red). DOCTRAP and CNN-GS correctly identified some EZ defects despite errors in the boundary segmentations.

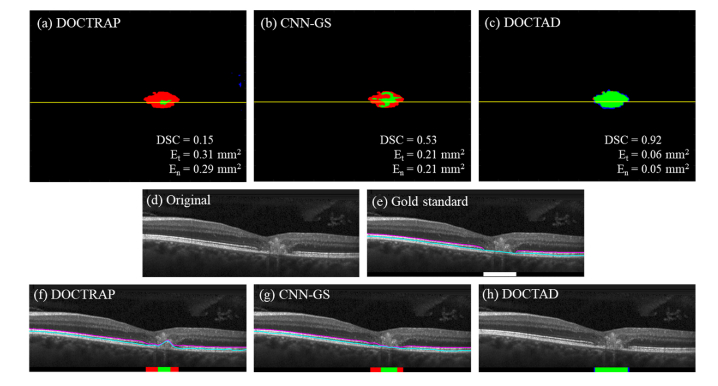
Fig. 7.

(a – c) Overlay of gold standard (manual) and predicted binary maps of EZ defects by DOCTRAP, CNN-GS, and our new DOCTAD method showing TP (green), FP (blue) and FN (red). (d) B-scan from the position marked by the yellow line on (a-c). (e) Gold standard (manual) boundary segmentations and EZ defect areas (white). (f – h) Boundary segmentations and predicted EZ defect areas by DOCTRAP, CNN-GS, and DOCTAD showing TP (green), FP (blue) and FN (red). DOCTRAP correctly identified some EZ defects despite errors in the boundary segmentations whereas CNN-GS correctly identified more EZ defects with more accurate boundary segmentations.

3.2 Improvements with longitudinal transfer learning

Next, we studied the effect of fine-tuning DOCTAD for a specific subject’s eye as described in Section 2.6. For each subject’s eye, we fine-tuned the CNN trained on the baseline volumes for which the subject was not included in the initial training set. To demonstrate that any improvement in performance was due to the usage of the subject’s baseline volume during fine-tuning instead of simply an extended training time, we also fine-tuned the CNN on the initial training set using the same methodology and parameters as in the proposed longitudinal transfer learning procedure. Performance was evaluated on the 6-month volume of the corresponding eye both before and after fine-tuning. We used the Wilcoxon signed-rank test to determine the statistical significance of the observed differences. Table 2 shows the average performance metrics of DOCTAD on the 6-month volumes before and after fine-tuning.

Table 2. Performance metrics (mean ± standard deviation, median) of DOCTAD on 134 6-month volumes before and after fine-tuning both on the initial training set and the subject’s baseline volume using 6-fold cross validation. Statistically significant differences (p-value < 0.05) are shown in bold.

Volumes	Performance metric	Method
		Gold standard (Manual)	Before fine-tuning	After fine-tuning
				On initial training set	On baseline volume
All	EZ defect areas (mm2)	0.71 ± 0.71, 0.54	0.74 ± 0.70, 0.56	0.76 ± 0.72, 0.60	0.78 ± 0.74, 0.61
	DSC	-	0.82 ± 0.16, 0.88	0.82 ± 0.17, 0.88	0.83 ± 0.17, 0.89
	Et (mm2)	-	0.18 ± 0.20, 0.12	0.18 ± 0.20, 0.12	0.17 ± 0.21, 0.11
	En (mm2)	-	0.11 ± 0.17, 0.06	0.12 ± 0.17, 0.06	0.11 ± 0.20, 0.06
CS	EZ defect areas (mm2)	0.87 ± 0.71, 0.70	0.89 ± 0.69, 0.73	0.92 ± 0.71, 0.76	0.93 ± 0.73, 0.76
	DSC	-	0.85 ± 0.12, 0.89	0.85 ± 0.12, 0.89	0.87 ± 0.10, 0.90
	Et (mm2)	-	0.21 ± 0.21, 0.14	0.21 ± 0.21, 0.14	0.20 ± 0.22, 0.13
	En (mm2)	-	0.13 ± 0.18, 0.07	0.13 ± 0.18, 0.08	0.12 ± 0.21, 0.07

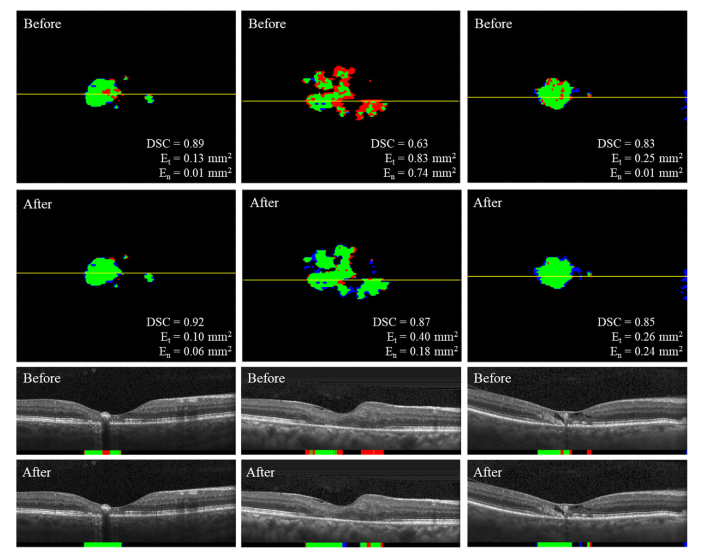
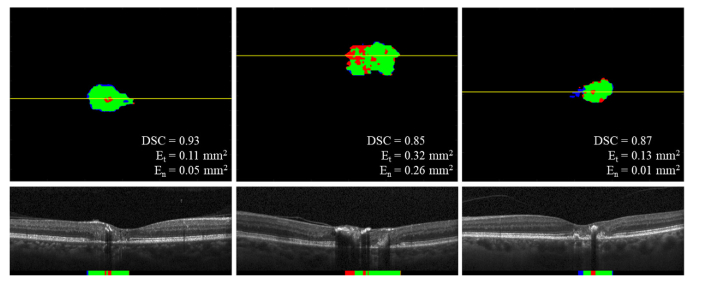
Overall, fine-tuning on the subject’s baseline volume resulted in an improved performance when predicting EZ defect areas. There was a significant increase in DSC especially for the 109 CS volumes, and decreased errors in the predicted EZ defect areas. Figure 8 shows examples of predicted EZ defect areas on the 6-month volumes before and after fine-tuning on the subject’s baseline volume. In contrast, fine-tuning on the initial training set did not result in comparable performance improvement overall.

Fig. 8.

Predicted binary maps of EZ defects on the 6-month volumes by DOCTAD before and after fine-tuning on the subject’s baseline volume showing TP (green), FP (blue), FN (red) and B-scans corresponding to the position marked by the yellow lines. Fine-tuning improved the EZ defects segmentations.

A major challenge in developing transfer learning techniques is to produce positive transfer (improved performance) while avoiding negative transfer (reduced performance) which in practice, is difficult to achieve simultaneously [72]. In our case, negative transfer may occur when the CNN overfits to features in the baseline volume that do not generalize to the 6-month volume, such as noise patterns in the images. Therefore, while there was an overall improvement across all volumes, there were some instances in which the performance on the 6-month volume did not improve following the longitudinal transfer learning procedure, either due to overfitting, or if the CNN was not updated during the fine-tuning as described in Section 2.6 (unchanged performance). Additionally, it is also possible that there is an improvement in one performance metric but a reduction in another. Table 3 shows the breakdown of the effect of the longitudinal transfer learning procedure on the performance of individual volumes.

Table 3. Performance breakdown on 134 6-month volumes after fine-tuning on the subject’s baseline volume.

Volumes	Performance metric	Percentage of volumes (%)
		Unchanged performance	Improved performance	Reduced performance
All	DSC	26	41	33
	Et (mm2)	26	43	31
	En (mm2)	26	38	36
CS	DSC	22	46	32
	Et (mm2)	22	44	34
	En (mm2)	22	41	37

3.3 Qualitative analysis

Upon qualitative assessment of the EZ defects segmentations by DOCTAD, there was good agreement between the gold standard and predicted binary maps of EZ defects. Some of the false positives or “over-prediction” could be associated with borderline-defective areas. We refer to borderline-defective areas as areas where the EZ is certainly diseased, but it is not clear if it is completely lost or is in transition to become completely defective. These are difficult to classify even for expert Readers and are subject to judgment calls, which may be inconsistent among different Readers. Figure 9 shows examples of some false positives associated with borderline-defective areas.

Fig. 9.

Predicted binary maps of EZ defects by DOCTAD showing TP (green), FP (blue), FN (red) and B-scans corresponding to the position marked by the yellow lines. The false positives (blue) occurred in borderline-defective areas.

On the other hand, some of the false negatives or “under-prediction” could be associated with the CNN’s limited field of view, as it only “sees” clusters. If a cluster was from a region where the retina was partially obscured, usually by shadowing from overlying blood vessels or intra-retinal pigment, DOCTAD was likely to make a prediction error. Figure 10 shows examples of false negatives associated with regions obscured by intra-retinal pigment.

Fig. 10.

Predicted binary maps of EZ defects by DOCTAD showing TP (green), FP (blue), FN (red) and B-scans corresponding to the position marked by the yellow lines. The false negatives (red) occurred in regions obscured by intra-retinal pigment.

One of the main motivations for developing a method to automatically segment EZ defects is to replace the time-consuming and subjective task of manual segmentation. Despite the careful review and manual correction of the EZ layer boundaries in the thousands of images by the expert Readers, there were occasional errors in the gold standard manual segmentations. Figure 11 shows an example of a manual segmentation error in the gold standard that was correctly identified by DOCTAD as EZ defects.

Fig. 11.

(a) B-scan with EZ defects that was missed in the gold standard (manual) segmentation (yellow arrow). (b) Gold standard (manual) boundary segmentations and EZ defects areas (white). (c) Predicted EZ defects areas by DOCTAD showing TP (green), FP (blue) and FN (red). The missed EZ defects (yellow arrow) were correctly identified but considered false positives (blue).

4. Conclusions

We have developed DOCTAD, a novel deep learning-based method to automatically segment EZ defects on SD-OCT images from eyes with MacTel2. We developed and trained DOCTAD to classify clusters of A-scans as normal or defective to create an en face binary map of EZ defects given a SD-OCT volume of an eye. Our method can localize and quantify EZ defects accurately compared to the gold standard manual segmentation. It does not require any segmentation of retinal layer boundaries as an intermediate step and outperforms two popular retinal layer boundary segmentation algorithms – DOCTRAP [27, 28] and CNN-GS [48]. It achieved a higher mean DSC of 0.86 on 107 CS volumes, compared to a mean DSC of 0.05 and 0.52 achieved by DOCTRAP and CNN-GS, respectively.

We further demonstrated that when longitudinal information was available, DOCTAD could be fine-tuned for a specific subject to improve the segmentation at future time points. In our experiments, subjects were imaged at two time points – baseline and 6-month. With fine-tuning using the baseline volumes, a higher mean DSC of 0.87 was achieved on 109 CS 6-month volumes, compared to a mean DSC of 0.85 achieved without fine-tuning. The fine-tuning procedure can be continuously applied as more images are collected over time to improve the segmentation performance of DOCTAD. We expect that volumes that did not benefit from the longitudinal transfer learning procedure at the 6-month time point may do so at a future time point.

DOCTAD’s average segmentation speed of 12 seconds per volume is fast enough for most clinical applications. Yet, some niche applications such as real-time OCT-guided ocular surgery require even faster execution times [73]. Currently, the segmentation time is limited by the need to extract and process clusters for every A-scan. In the future, we plan to adapt our method to process the 3-D SD-OCT volumes as a whole without the need for cluster extraction by adapting 3-D CNNs for volumetric segmentation [74–76] to automatically segment and additionally, project EZ defects onto 2-D en face images, which would decrease the segmentation time. While 5 minutes is needed for the longitudinal transfer learning procedure, this step is often implemented offline during the 6-month period between each imaging time point.

The errors in the predicted EZ defect areas by DOCTAD could be in large associated with borderline-defective areas, or regions obscured by blood vessels or intra-retinal pigment. While we expect that using larger clusters may mitigate to a certain degree the false negatives associated with regions obscured by blood vessels or intra-retinal pigment, it would also increase the likelihood of false positives and the computation time. Additionally, in some cases, such as the first example shown in Fig. 8, the proposed longitudinal transfer learning procedure was able to correct some of these false negatives. Also, although the study data set was reviewed and corrected by two expert OCT Readers, we found (albeit rare) instances of manual segmentation error, which further highlights the need for an objective and consistent automatic segmentation method. An example is shown in Fig. 11, where upon image review it was deemed that DOCTAD correctly detected a region of EZ defects missed by the manual Readers. Such errors naturally occur when manually segmenting large data sets in a multi-center clinical trial. We did not alter manual segmentation when calculating the overall error of DOCTAD, so we would not bias the reported results in favor of our algorithm. While we expect that in the near future clinical trials will still utilize the current approach of semi-automatic segmentation, we expect that utilization of our deep learning method will significantly reduce the workload and will improve the accuracy of semi-automatic grading.

Funding

The Lowy Medical Research Institute; National Institutes of Health (NIH) (R01 EY022691 and P30 EY005722); Google Faculty Research Award; 2018 Unrestricted Grant from Research to Prevent Blindness.

Disclosures

The authors declare that there are no conflicts of interest related to this article.