Metal–insulator-transition engineering by modulation tilt-control in perovskite nickelates for room temperature optical switching

Significance

Correlated transition metal oxide perovskites receive a lot of attention due to their unique physical properties, which are largely driven by distortion of the BO₆ octahedral network. In bulk, the control of the octahedral network is normally obtained by cation substitutions in a random alloy. Similar to the charge donors in semiconductors, cation substitutions will introduce scattering and disorder. The development of artificial heterostructures offers unprecedented opportunities to lattice engineering to achieve desired properties. In this work, we demonstrated a structural analogue of modulation doping in nickelate heterostructures through the interfacial transfer of tilt patterns. Modulation tilt control was used to remotely control the Ni–O bonds in the compound SmNiO₃ and thereby its critical temperature for optimal optical switching application.

Abstract

In transition metal perovskites ABO₃, the physical properties are largely driven by the rotations of the BO₆ octahedra, which can be tuned in thin films through strain and dimensionality control. However, both approaches have fundamental and practical limitations due to discrete and indirect variations in bond angles, bond lengths, and film symmetry by using commercially available substrates. Here, we introduce modulation tilt control as an approach to tune the ground state of perovskite oxide thin films by acting explicitly on the oxygen octahedra rotation modes—that is, directly on the bond angles. By intercalating the prototype SmNiO₃ target material with a tilt-control layer, we cause the system to change the natural amplitude of a given rotation mode without affecting the interactions. In contrast to strain and dimensionality engineering, our method enables a continuous fine-tuning of the materials’ properties. This is achieved through two independent adjustable parameters: the nature of the tilt-control material (through its symmetry, elastic constants, and oxygen rotation angles), and the relative thicknesses of the target and tilt-control materials. As a result, a magnetic and electronic phase diagram can be obtained, normally only accessible by A-site element substitution, within the single SmNiO₃ compound. With this unique approach, we successfully adjusted the metal–insulator transition (MIT) to room temperature to fulfill the desired conditions for optical switching applications.

Oxide heterostructures offer unprecedented opportunities to manipulate the interplay between spin, charge, orbital, and lattice degrees of freedom, leading to many novel electronic phases that are hard or even impossible to be realized in bulk materials (1–7). To date, strain and dimensionality are two main approaches used to engineer properties of heterostructures (in oxides ranging from dielectric or ferroelectric insulators to superconductors). While both can strongly modify the physical response of the materials (1–5), they suffer several limitations, in particular in the context of oxide perovskites whose physical properties are largely driven by the metal–oxygen bond angles (8–10). First, the strain and dimensionality engineering are both discrete handles with restricted tuning possibilities. The strain is applied through the growth on a handful of commercial substrates that have preset lattice constants, and the small lattice mismatch that is required for coherent epitaxial growth further limits the choice of substrates. Dimensionality is tuned by reducing the number of unit cells one-by-one, and a significant effect only occurs when the thickness is in the range of a few unit cells. Second, the strain often acts in an indirect manner: It will influence the bond angles but also the bond lengths, which can result in nonsystematic behavior.

The nickelates have been attracting enormous attention owing to their intriguing properties (4, 7, 10–15). One of the remarkable properties is the metal–insulator transition (MIT), which in the bulk can be continuously adjusted by tolerance factor or external pressure (10, 16), serving as a fascinating platform for both fundamental physics investigation and synaptic applications (11–19). Very recently, Mercy et al. (19) identified that the breathing mode responsible for the MIT in the perovskite nickelates is triggered by octahedral rotations and tilts. This makes the nickelates an ideal system for exploring emergent functionalities through the direct control of angles between neighboring octahedra.

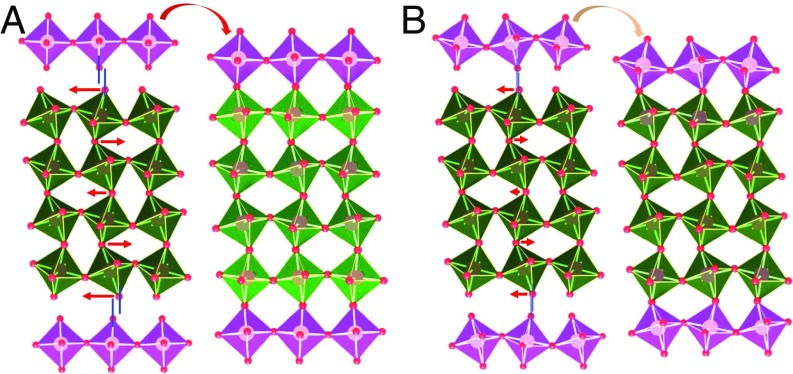
In this work, we introduce modulation tilt control as an approach to tune the ground state of nickelate thin films by directly acting on the oxygen octahedral rotation modes. Through intercalating the target material with a tilt-control layer (TCL) as shown by the sketch in Fig. 1, the natural amplitude of a given rotation mode will be modified to retain the connectivity of the octahedral network (20, 21), leading to strong propagation of the tilt around the in-plane axes. As also shown in Fig. 1A, a less tilted TCL can significantly reduce the tilt in the target material. If the tilt of TCL is similar to the target material, the structure modulation effect then will be very small (Fig. 1B). Additionally, the decay nature of tilt propagation should allow us to modulate the tilt by changing the thickness of the target material. In contrast with strain and dimensionality engineering, our method enables a pseudocontinuous fine-tuning of the materials’ properties. This is achieved through two independent adjustable parameters: the nature of the tilt-control material (through its symmetry, elastic constants, and oxygen rotation angles), and the relative thicknesses of the target and tilt-control materials. In a prototypical system where we combine SmNiO₃ (SNO) with TCLs in fine period TCL/SNO superlattices (SLs), we are able to directly act on the SNO octahedral rotation mode and therefore continuously tune the MIT. Our results show that a magnetic and electronic nickelate phase diagram, normally built through A-site element substitution, can be demonstrated in a single SNO compound through the transfer of tilt patterns. This remote control of ground state properties, not through doping but here through the transfer of tilt patterns, can be viewed as a structural analog of modulation doping in semiconductors. This approach paves a way for novel phases in oxides that remain inaccessible by simple composition modulations. Moreover, it offers a method to adjust materials to meet practical conditions for applications.

Fig. 1.

Octahedral tilt pattern modulation. Schematic view of octahedral tilt modulation (green layer) by introducing a tilt-control layer (purple layer) having (A) less tilting and (B) more tilting. Here, an orthorhombic structure (a⁺b⁻b⁻) is used for demonstration. The red arrows and their lengths indicate the direction and amount of the rotation angle change, respectively, which are necessary to match TCL. A smaller tilt change in interior layers is due to the decay nature of interfacial geometry constraint.

Results

Nickelate SLs were grown on atomically flat NdGaO₃ (NGO) (110) substrates by pulsed laser deposition (PLD) (SI Appendix, section 1). LaFeO₃ (LFO) was chosen as the TCL layer because LFO is less tilted than SNO, and it also shares same polar nature and orthorhombic symmetry as SNO. Additionally, a large compressive strain (1.8%) enforced by the NGO substrate will further reduce the tilt of LFO (22, 23). Therefore, a strong tilt modulation of SNO by LFO can be expected. Four unit cells (uc) of LFO were deposited first, and subsequently, the (LFO₁/SNO_n)_m SLs (noted as LFO₁–SNO_n) were grown starting from SNO. The total SNO thickness (n × m) was maintained at ∼40 uc. The SNO films and LFO₁–SNO_n SLs share the same orthorhombic symmetry as characterized by X-ray diffraction (SI Appendix, section 2). Due to the presence of LFO, the LFO₁–SNO_n SLs are found to exhibit less structural distortion compared with pure SNO films.

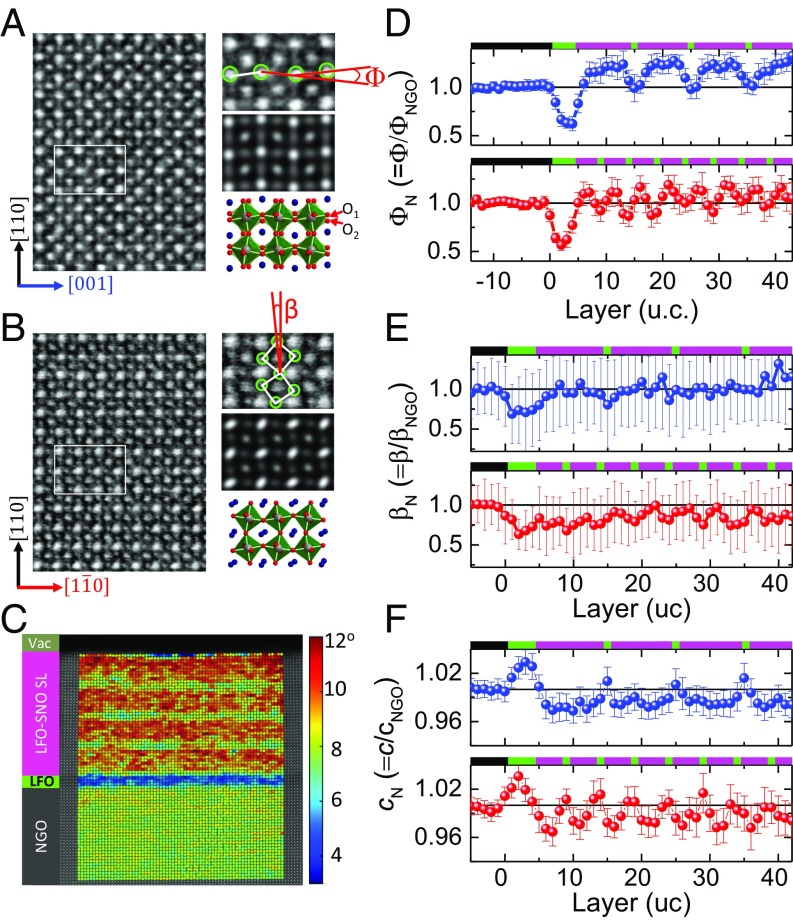
The layer-resolved lattice distortion of nickelate SLs was investigated by scanning transmission electron microscopy (STEM). The orthorhombic symmetry produces out-of-phase tilts of amplitude (α_T) and in-phase rotations of amplitude (α_R) around the in-plane [1-10] and [001] axis, respectively. These rotational behaviors are revealed microscopically by resolving the oxygen sites in the annular bright field (ABF) images (Fig. 2 A and B). The limited contrast difference between LFO and SNO in STEM images is due to the similarity in atomic number for Sm and La, as well as Ni and Fe, but the chemical contrast can be resolved by electron energy loss spectroscopy (EELS) (SI Appendix, sections 3 and 4). The ABF image of the (1–10) plane displays significantly elongated and blurred oxygen sites, which are consistent with the signature of out-of-phase rotation that generates two very close oxygen columns (O₁ and O₂) (Fig. 2A). In the (001) plane, the atomically resolved oxygen sites clearly confirm the in-phase rotational behavior around the [001] axis (Fig. 2B).

Fig. 2.

Atomic scale lattice structural characterization. Inversed ABF images of LFO₁–SNO₄ with zone axis along (A) [1-10] and (B) [001] directions. (A and B, Right) Magnifications of a selected region (Top), simulated ABF-STEM images (Middle), and structural models of bulk SNO (Bottom) for comparison. (C) 2D mapping of antipolar A-site motions (Φ) in LFO₁–SNO₁₀. The Φ mapping is overlaid on a HAADF image from which the angle Φ is calculated. The profile of (D) antipolar motion (Φ), (E) octahedral tilt (β), and (F) out-of-plane lattice parameter c for LFO₁–SNO₄ (red) and LFO₁–SNO₁₀ (blue). (D–F, Top) The corresponding schematic view of chemical profiles with black (NGO), green (LFO), and purple (SNO).

Using statistical parameter estimation theory to quantify the atomic positions from a STEM image, we are able to obtain detailed, layer-resolved lattice structure parameters across the SLs (SI Appendix, section 5). Fig. 2C shows an example of the 2D mapping of the anti-polar A motion of LFO₁–SNO₁₀ SL, which is described by angle (Φ) (see definition in Fig. 2A). The angle Φ is correlated with amplitudes of rotations (α_R) and tilts (α_T) of the BO₆ octahedra: Φ ∼ α_R·α_T (24, 25). The layer-resolved profile of Φ in LFO₁–SNO₁₀ is shown in Fig. 2D. To avoid possible artifacts from the imaging technique itself, the profiles are normalized to the value of the NGO substrate (Φ_N = Φ/Φ_NGO). As shown in Fig. 2D, a relaxation of the angle Φ_N is observed within the central part of the first 4-uc LFO layer, while near both the bottom LFO/NGO and top SNO/LFO interfaces, this angle Φ_N is larger, as expected from the geometric constraint effect discussed above in Fig. 1. Within the SL region, a trapezoidal wave-like Φ_N-profile is observed with a minimum angle exhibited by the LFO single layer and a plateau in the central part of each SNO layer. Closer to the LFO layer, the Φ_N of SNO becomes smaller. Upon reducing the SNO to 4 uc, the whole SNO layer is now under the impact of interfacial structure constraint, and thus, the Φ_N-profile is changed into a more triangular wave-like shape.

The profiles of octahedral tilt angle β_N (= β/β_NGO) around the [001] axis (see definition in Fig. 2B) are estimated from ABF images (SI Appendix, section 5). This tilt angle β corresponds in fact to the projection of α_T on (001) planes. Similar to the antipolar distortion Φ_N, the β_N becomes smaller near the LFO/SNO interface, and a periodic modulation of β_N is observed across the SL as shown in Fig. 2E. The modulation of the β_N of SNO layer is weakened when the SNO thickness is increased from 4 to 10 uc. The stretching or bending of the Ni–O bond should also change the lattice constant. This scenario is confirmed from the profile of out-of-plane lattice constant (c). As shown in Fig. 2F, the lattice parameter c of LFO within the SL region is smaller than that in the 4-uc LFO buffer region. Near the LFO/SNO interface, the c of the SNO becomes larger than that in the central region of the SNO layer. The larger (smaller) c of LFO or SNO corresponds to smaller (larger) tilt in LFO or SNO (Fig. 2 D–F). The mean values <Φ_N> (<β_N>) of SNO in LFO₁–SNO₁₀ and LFO₁–SNO₄ SLs are 1.178 (0.976) and 1.049 (0.852), respectively. The reduced tilts and antipolar distortion demonstrate the effective control of octahedral distortion of SNO by intercalating the single LFO layer.

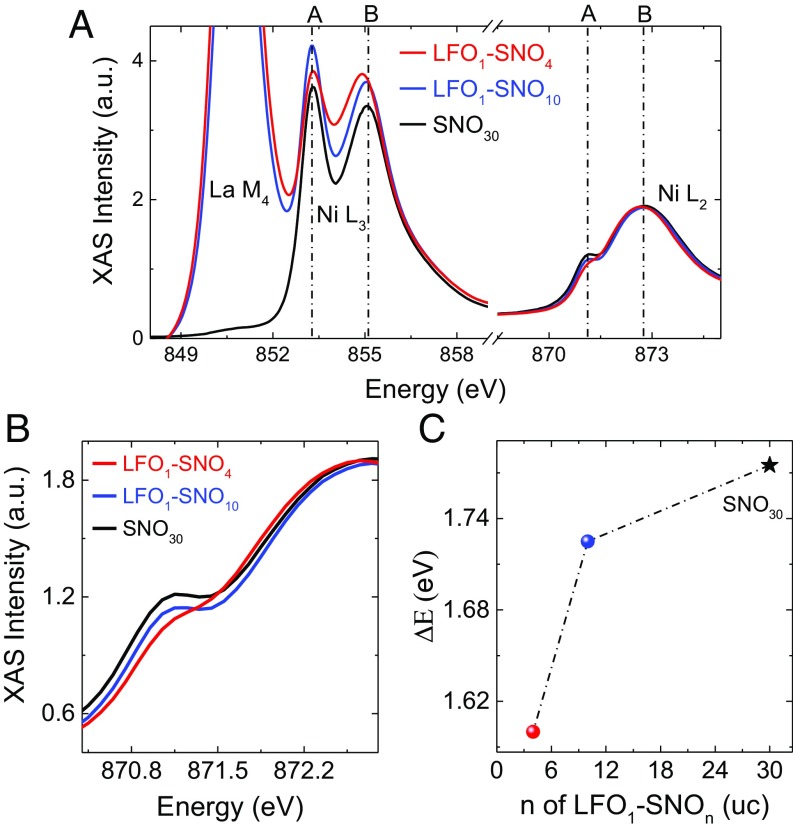
The electronic structures of SNO have been investigated by X-ray absorption spectroscopy (XAS). As shown in Fig. 3A, both Ni L₂ and L₃ edges are split into two (A and B) peaks as occurring in bulk RNiO₃ (26). The peak splitting energy ∆E (≡E_B − E_A) in LFO₁−SNO₄ is smaller than in LFO₁−SNO₁₀, while in LFO₁−SNO₁₀ is similar to that in SNO₃₀. As shown by the zoomed-in view of the Ni L₂ edge in Fig. 3B, the two split peaks gradually merge with decreasing SNO thickness in LFO₁−SNO_n. The ∆E for the Ni L₃ edge is shown in Fig. 3C, clearly illustrating a smaller splitting energy due to the structure modulation by LFO. The splitting of the Ni L edge is suggested to depend on both the magnitude of the breathing mode distortion and the size of the Ni–O–Ni hopping interaction (27). A smaller splitting energy indicates a smaller Ni–O–Ni interaction and a smaller breathing distortion [δd = (d_L − d_S)/2], where d_L and d_S are the long and short Ni–O bonds, respectively (27). The XAS of the Ni L_2,3 edge shown in Fig. 3A also suggests the absence of Ni²⁺ and no change of the valence of Ni, excluding possible charge transfer between LFO and SNO layers.

Fig. 3.

Electronic structure of nickelate SLs. (A) XAS of Ni L_2,3 edge. (B) Zoomed-in spectra of Ni L₂ edge. (C) Peak splitting energy ∆E = E_B − E_A of LFO₁–SNO_n SLs and SNO₃₀ film. The XAS was measured at 22 K.

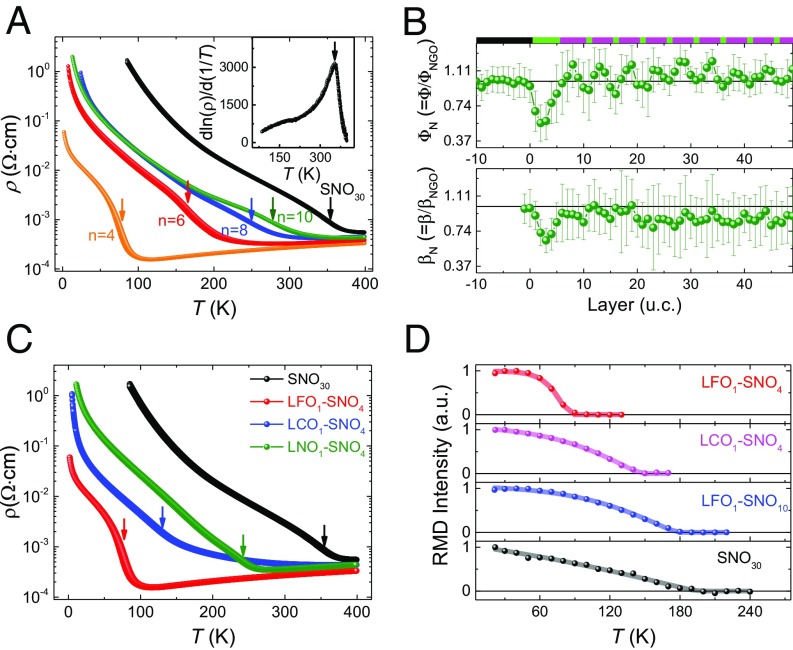
Concomitant to lattice and electronic structure modulations, a significant change of transport properties in LFO₁–SNO_n SLs has been achieved. As shown in Fig. 4A, a giant enhancement of conductivity is observed in LFO₁–SNO₄ SL. The characteristic MIT temperature T_MIT is reflected from the resistivity inflection point $\left(\frac{dln\rho }{d1/T}{|}_{\text{max}}\right)$ (28) as shown in Fig. 4A, Inset. The T_MIT of LFO₁–SNO₄ is 78 K, much lower than that of SNO₃₀ film (356 K). With increasing SNO thickness, the T_MIT moves toward that of bulk SNO films, coincident with the smaller structural modulation by LFO as the SNO thickness increases. The thickness (n) of SNO within LFO₁–SNO_n behaves similarly to the tolerance factor, monotonically controlling the transition temperatures (SI Appendix, section 6).

Fig. 4.

Transport and magnetic properties of tilt engineered nickelate SLs. (A) Temperature-dependent resistivity of LFO₁–SNO_n SLs (n = 4–10) and 30 uc SNO film (SNO₃₀). Inset shows the first derivative $\frac{dln\rho }{d1/T}$ of the SNO₃₀ sample. The arrows in A and C indicate the resistive inflection points derived from d$\frac{dln\rho }{d1/T}{|}_{\text{max}}$. (B) Layer-dependent profiles of antipolar motions (Φ) and octahedral tilt angle (β) of LCO₁–SNO₄ SL. The chemical profile is schematically shown on Top: black (NGO), green (LCO), and purple (SNO). (D) Temperature-dependent intensity of (1/4,1/4,1/4) magnetic Bragg reflection peak.

The decay nature of the geometric constraint imposed by the octahedral network across the interface allows us to rationally design the octahedral tilt distortion via either changing the thickness of the SNO layer or a delicate choice of the tilt-control layer. As an illustration of the designed functionality by engineering the nature of TCL, a LaCrO₃ (LCO) layer was used to fabricate a LCO₁–SNO₄ SL and compare with the LFO₁–SNO₄ SL. LCO shares the same orthorhombic structure and similar octahedral tilt with LFO but has a smaller lattice mismatch of 0.6% with NGO than LFO/NGO of 1.8%. LCO is expected to exhibit more bending of the Cr–O–Cr bond and, therefore, have less impact on the tilt of the SNO (22, 23). The effect of LCO on the SNO structural modulation was investigated as well by STEM, as shown in Fig. 4B. Near the LCO/SNO interface, both the Φ_N and β_N of SNO are found to be reduced as occurring in LFO₁–SNO₄. However, the <Φ_N> and <β_N> of SNO within LCO₁–SNO₄ SL are 1.079 and 0.890, respectively, bigger than the values for LFO₁–SNO₄, as mentioned above. Accordingly, the LCO₁–SNO₄ SL shows higher conductivity than nonengineered SNO₃₀ but is less conductive than the LFO₁–SNO₄ SL (Fig. 4C). The significant impact from LFO is further illustrated by comparing to the (LaNiO₃)₁–SNO₄ (LNO₁–SNO₄) SL. As shown in Fig. 4C, LNO₁–SNO₄ exhibits a much higher T_MIT (=240 K) than LFO₁–SNO₄. Although LNO has a little smaller tilt in bulk (5.3°) than that of bulk LFO (6.8°), the LNO layer is under tensile strain, which increases the tilt, in contrast to the highly compressive strain imposed on the LFO layer. The higher conductivity in LFO₁–SNO₄ than LNO₁–SNO₄ further reveals a pivotal role of the structural effect rather than any possible chemical reconstruction at the interface.

In addition, the Néel temperature (T_N) was measured using resonant magnetic diffraction (RMD) (27, 29). The RMD signal was taken at the Ni L₃ resonance. Fig. 4D displays the temperature-dependent intensity of the (1/4,1/4,1/4) magnetic Bragg reflection peak, which arises from the E′-type antiferromagnetic (E′-AFM) ordering of the nickelates. The Néel temperature is found to vary significantly when introducing interfacial structure modulation. The T_N of the SNO₃₀ film is ∼194 K, while it is ∼85 K for the LFO₁–SNO₄. For LFO₁–SNO₁₀, the effect of the LFO layer becomes weaker and the T_N is around 176 K, close to the SNO₃₀ film. The T_N of LCO₁–SNO₄ is ∼146 K, in between LFO₁–SNO₄ and LFO₁–SNO₁₀.

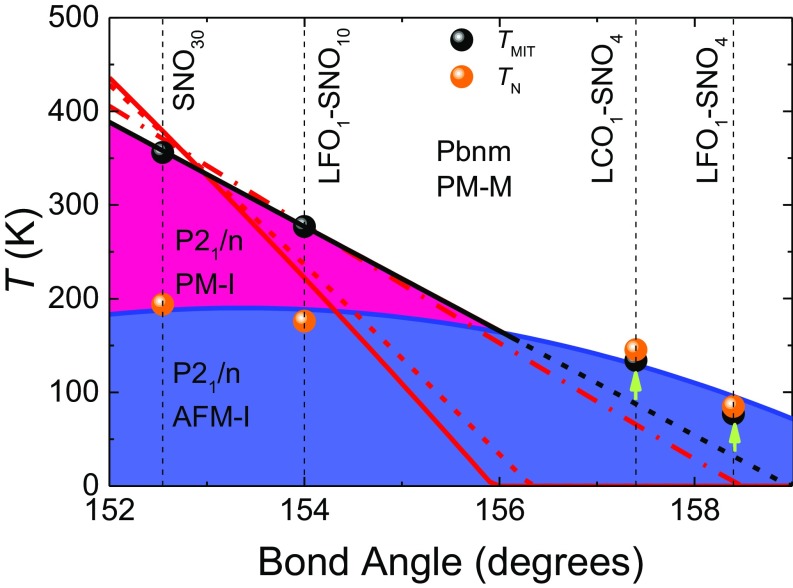
With the obtained T_N and T_MIT, a phase diagram is constructed using the mean Ni–O–Ni bond angle as a control parameter (Fig. 5). Here, the mean Ni–O–Ni bond angles are converted from mean values of β_N (see Materials and Methods). It is found that the T_MIT monotonically changes with the bond angle. For films with relatively small Ni–O–Ni bond angles and large T_MIT (>∼200 K), T_N and T_MIT are decoupled and T_MIT decreases relatively abruptly as the bond angle increases. According to that trend, T_MIT should be below T_N at large bond angles; in that region, however, the T_MIT is further promoted by the appearance of the E′-type AFM order and T_MIT becomes pinned at T_N, in line with the discussion in ref. 19 and in agreement with bulk phase diagram (10). Therefore, the geometric design of the octahedral network produces a bulk-like phase diagram of the whole nickelate family but using only one compound SNO (Fig. 5 and SI Appendix, section 6). Our results also highlight the effect of local octahedral distortion at the atomic scale on the nickelate electronic states, confirming the central role the NiO₆ octahedral tilt in determining the properties of nickelates.

Fig. 5.

Temperature phase diagram of nickelate SLs as a function of the mean Ni–O–Ni bond angle. The mean bond angle is converted from mean tilt angle α_T (see Materials and Methods). The black dots (T_MIT) and orange dots (T_N) are experimental data. The theoretical evolution of T_MIT has been estimated while constraining the tilt angle α_T as imposed by the TCL and (i) relaxing self-consistently the rotation angle α_R (∆α_R ∼ −1.5%, full red line), (ii) constraining the rotation angle to keep it fixed (∆α_R = 0%, dashed red line), or (iii) constraining further the rotation angle to increase it slightly (∆α_R ∼ +3%, dash-dot red line). See Materials and Methods for the explanation of the parameter ∆α_R.

The explicit link between the controlled amplitude of the Ni–O–Ni bond angle and the observed evolution of T_MIT can be further supported theoretically using the Landau-type model of ref. 19, assigning the MIT to a triggered phase transition arising from the softening of the breathing distortion by oxygen tilts and rotation and with parameters directly derived from first principles. Starting from the set of parameters associated to the effective tolerance factor yielding a T_MIT equal to that of SNO₃₀, we can mimic the role of the TCL by forcing artificially the tilt mode amplitude (i.e., rescaling its energy curvature; see Materials and Methods) and investigating the subsequent impact on T_MIT. This can be done while allowing self-consistent relaxation of the rotation mode or by constraining it additionally so that it remains constant or is slightly amplified. The predictions of the model are summarized in Fig. 5 and compared with the experimentally obtained correlation between T_MIT and the bond angle. Note that here the model is restricted to structural degrees of freedom and neglects the emergence of a magnetic order at T_N. The agreement observed between theory and experiment confirms the central role of the oxygen tilts in tuning T_MIT. The model further suggests that rotations might be slightly amplified as the tilts are reduced.

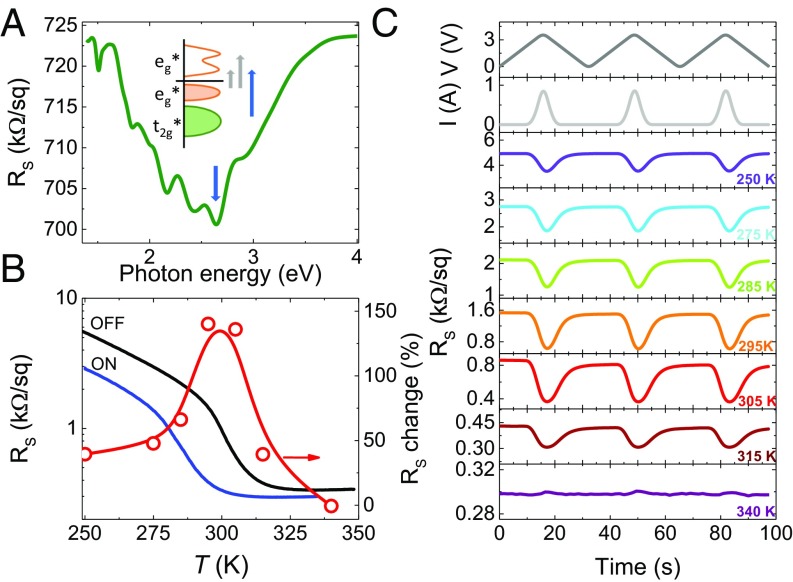
This efficient tuning is exploited practically to move T_MIT close to room temperature and switch the resistance by an external stimulus. Here, we propose and use an approach to tune the resistance of nickelates through light illumination at specific wavelengths. Fig. 6A, Inset presents a sketch of the electronic structure of a nickelate in its insulating phase as usually understood today. The conduction band is formed by e_g* states (antibonding states between Ni 3d and O 2p states, of predominant oxygen character) whose density of states shows a double peak shape with a local minimum (30). Below the Fermi level, the valence band has a similar character, in line with the negative-charge transfer nature of nickelates. Further down in energy lie the t_2g* states, with dominant Ni 3d character. This electronic structure allows for three main optical transitions (Fig. 6A, Inset) (31). The deeper t_2g* to e_g* state transition (blue arrow) corresponds to transferring electrons from a 3d-like state to an O 2p-like state. Given that the occupancy of O 2p states is directly related to the level of covalence, a t_2g* → e_g* transition should intensify the covalent character and then enhance conductivity (15). More generally, photo transfer of electrons from large to small Ni cages will bring the system closer to the metallic electronic configuration of the Pbnm phase.

Fig. 6.

Light-induced resistance switching in nickelate SLs. (A) Dependence of the sheet resistance with illuminating photon energy at 70 K for a NNO₁–SNO₂ SL. The sketch describes the different optical transitions in nickelates, and the down-pointing blue arrow shows the energy corresponding to the t_2g* → e_g* transition at ∼2.7 eV. (B) Temperature dependence of the sheet resistance of NNO₁–SNO₂ SL (left axis) without (black) and with illumination (blue) with a blue LED (hν = 2.69 eV) powered with 1 A. Relative resistance change (right axis) induced by illumination. The symbols (right axis) correspond to the data of C. (C, Top two) Voltage and current applied to the blue LED vs. time. (C, Bottom seven) Time dependence of the resistance upon illuminating the NNO₁–SNO₂ sample with the blue LED at different temperatures.

To realize room temperature oxide electronics for practical applications, several different TCLs have been explored to induce a first-order room temperature MIT, and NdNiO₃ (NNO) is found to be an ideal candidate (Fig. 4 and SI Appendix, section 7). A first-order MIT near room temperature was obtained in a (NNO₁/SNO₂)₁₀ (NNO₁–SNO₂) SL (SI Appendix, section 7). Fig. 6A shows its resistance at 70 K (well into the insulating state) upon low-power illumination at different photon energies. The resistance shows a minimum for an energy corresponding to the t_2g* → e_g* transition, which is consistent with the photo-doping mechanism described above. Fig. 6B presents the temperature dependence of the resistance of the sample with and without 2.69 eV high-power blue light, nonisothermal illumination. The MIT temperature shifts down by ∼20 K with the light on, yielding a maximum light-induced resistance change near 300 K. Fig. 6C shows the evolution of the resistance upon illumination with blue light pulses at different temperatures. Consistent with the data in Fig. 6B, the resistance switching effect is maximized at 300 K, amounting to nearly 150%. In SI Appendix, we show data for isothermal illumination and for a LFO₁–SNO₁₀ SL. Since we were using long illumination pulses, sample heating due to light absorption was probably the main process at play, causing an apparent shift of the MIT temperature. However, the observed maximum optical switching near room temperature would strongly imply that the photo-doping mechanism proposed above should also yield a resistance switching effect for ultrafast (sub ps) pulses with a photon energy corresponding to the t_2g* → e_g* transition (see also SI Appendix, section 8). In any case, our data qualify engineered nickelates as room temperature photoresistors based on a correlated material.

Discussion and Conclusion

In conclusion, we demonstrated the remote control of ground state properties of nickelates through interfacial tilt pattern modulation using a TCL. By manipulating two independent adjustable parameters—the nature of the tilt-control material, and the relative thicknesses of the target and tilt-control materials—we obtained pseudocontinuous modulation of octahedral tilt and fine-tuning of the materials’ properties. Our results visualized the monotonic change of the MIT with varying octahedral tilt, remarkably underlining the role of the Ni–O–Ni bond angle in determining the electronic ground state of the nickelates and supporting the structurally triggered mechanism proposed in ref. 19. By finely tuning the oxygen network, we are already able to achieve a near-room temperature MIT and a giant room temperature optical switching of resistance. The interfacial tilt pattern modulation using a TCL can be viewed as a structural analog of modulation doping in semiconductors, which has been a breakthrough discovery and led to both the observation of the fractional quantum Hall effect and to faster microelectronic circuits. This interface modulation tilt control can be applied directly to other perovksite materials, opening up new perspectives for the rational design of new classes of quantum materials for next-generation electronics applications.

Materials and Methods

The SNO, LNO, LFO, and LCO films or layers were deposited on atomic flat NGO substrates at a laser fluence of 2 J/cm² by PLD technique. The XRD was performed by PANalytical-X’Pert materials research diffractometer (MRD) at high-resolution mode. Transport properties were measured by using a Quantum Design Physical Properties Measurement System (PPMS) in a van-der-Pauw geometry.

STEM was performed on the Qu-Ant-EM instrument at the University of Antwerp. Cross-sectional cuts of the samples along the [1-10] and [001] directions were prepared using a FEI Helios 650 dual-beam Focused Ion Beam device. Satisfactory samples were prepared using low-energy ion beam final thinning subsequent to a protection of the sample surface by sputtering of a 30 nm-thick carbon protection layer, followed by E-beam deposition of Platinum as a first step to the FIB lamella preparation procedure. For imaging and EELS, the microscope was operated in STEM at 300 kV acceleration voltage with a convergence semiangle of 21 mrad, providing a probe size of ∼0.8 Å. The collection semiangle are 8 to 17 mrad and 44–190 mrad for ABF and high-angle annular dark field (HAADF) imaging, respectively. The collection angle for EELS was 69 mrad. Image processing and analysis is detailed in SI Appendix. Simulations of ABF-STEM images of SNO along [001]_or and [1-10]_or zone axes were made with QSTEM at conditions of probe size 0.7 Å, 300 kV, de focus −1.7 nm, C3 = 1 μm, convergence angle 21 mrad, 15 configurations for TDS, collection angle 8–17 mrad, and 15 nm thickness.

The XAS and RMD were performed using an in-vacuum four-circle diffractometer at the Resonant Elastic and Inelastic X-Ray Scattering (REIXS) beamline at Canadian Light Source (CLS) in Saskatoon, Canada. The beamline has a flux of 5 × 10¹² photons per second and photon energy resolution of 10⁻⁴ eV. The base pressure of the diffractometer chamber was kept lower than 10⁻⁹ Torr. The XAS spectra were measured using the total electron yield method, with the incident photons at an angle of 30° from the surface. At the Ni L_2,3 edge, measurements with π and σ polarizations were averaged.

The Landau-type modeling was performed relying on the expression provided in ref. 19 and related set of parameters directly fitted from first-principles DFT calculations (see supplementary material in ref. 19). The effective tolerance factor was selected to get a MIT corresponding to that experimentally observed in the SNO₃₀ sample (T_MIT = 356 K). Then, to mimic the role of the TCL on the tilt mode, the energy curvature of the latter was renormalized by adding a prefactor (1 − x) in front of the tilt quadratic coefficient. Tuning x, we can get the evolution of the tilt amplitude at room temperature (α_T directly linked to the Ni–O–Ni bond angle) and of the corresponding T_MIT in terms of the external constraint imposed on the tilt mode. Results are reported in Fig. 5, in which we plot the evolution of T_MIT with respect to that of the Ni–O–Ni bond angle at room temperature for direct comparison with experimental data. Since tilt and rotation modes are coupled within the Landau model through a biquadratic term, tuning the tilt amplitude also indirectly affects the rotation angle. Since we have no direct information on the effects of the TCL and epitaxial strain on the latter, calculations were performed (i) relaxing self-consistently the rotation angle α_R, which progressively evolves with α_T (for the largest constraint imposed on α_T in Fig. 5, the deviation of α_R at T_MIT with respect to its natural amplitude—i.e., value in bulk without constraint—is ∆α_R ∼ −1.5%); (ii) constraining the rotation angle to force it to remain unaffected (∆α_R = 0%); and (iii) constraining the rotation angle to increase it slightly (here the coupling between rotations and tilts has been slightly modified so that for the largest constraint imposed on α_T in Fig. 5, ∆α_R ∼ +3%). The tilt angle amplitude α_T, as accessible from the Landau model, and its projection on (001) planes, as measured experimentally, are both related to the Ni–O–Ni bond angle reported in Fig. 5 through θ = 180 − 2 α_T = 2 sin⁻¹ [1/(1 + 2 tan² β)^1/2].

Transport measurements under illumination were performed in a cryostation provided by Montana Instrument with uncoated windows presenting 90% transmittance in the visible range. Two different configurations were used for characterizing the thermal response of the samples. In setup 1, the layer was thermally connected to the cold finger of the cryostat. To do so, we added thermal grease to the edges of the sample in such a way that the NGO substrate was thermally connected to the sample holder. In setup 2, an insulating layer was added between the sample and the sample holder such that there was no thermal contact between the layer and the cold finger of the cryostat. The sheet resistance was determined by biasing with a current of 10 µA.