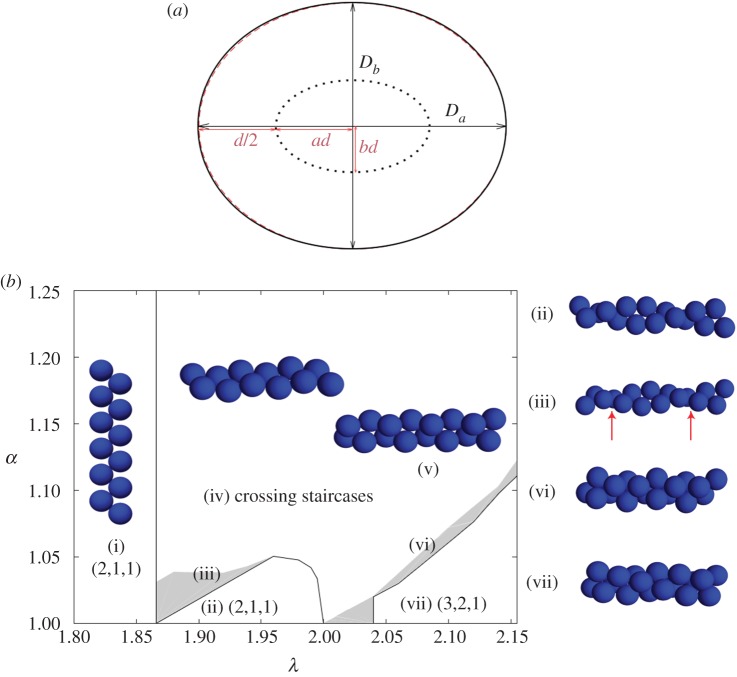
Figure 4.
Elliptical cylinders favour the staircase arrangement of hard spheres in simulations. (a) Cross section of elliptical cylinder model. During the SLP optimization, hard sphere centres of diameter d evolve on the surface of an elliptical cylinder (dotted curve) with semi-major axis ad and semi-minor axis bd. The resulting boundary confinement (black solid curve) is approximately elliptical (red dashed curve) with major and minor diameters Da and Db, respectively, when α = Da/Db is small. The case α = 1.25 is depicted here. (b) Diagram of the densest packings of hard spheres in cylinders of width up to λ = 2.15 and an elliptical aspect ratio α. Sharp transitions (solid lines) are observed between certain structures. Because of the competition between packing helicity and cylinder ellipticity, however, helicity is lost in two steps. It becomes discontinuous (solid line), before slowly vanishing (grey zones). Sample structures of (i) staircase (2,1,1) and (ii) twisted staircase (2,1,1); (iii) transitional defective (red arrows) structure between staircase and twisted staircase; (iv) and (v) crossing staircase (see text); (vi) triple helix (3,2,1); and (vii) transitional structure between (3,2,1) and crossing staircase regimes. The regime of staircase and twisted staircase is markedly enlarged for α > 1. Note, however, that in this model the bamboo structure is only stable at λ = 1, and the hopscotch structure is always unstable. (Online version in colour.)