Three-dimensional simulation of the Caenorhabditis elegans body and muscle cells in liquid and gel environments for behavioural analysis

Abstract

To better understand how a nervous system controls the movements of an organism, we have created a three-dimensional computational biomechanical model of the Caenorhabditis elegans body based on real anatomical structure. The body model is created with a particle system–based simulation engine known as Sibernetic, which implements the smoothed particle–hydrodynamics algorithm. The model includes an elastic body-wall cuticle subject to hydrostatic pressure. This cuticle is then driven by body-wall muscle cells that contract and relax, whose positions and shape are mapped from C. elegans anatomy, and determined from light microscopy and electron micrograph data. We show that by using different muscle activation patterns, this model is capable of producing C. elegans-like behaviours, including crawling and swimming locomotion in environments with different viscosities, while fitting multiple additional known biomechanical properties of the animal.

 This article is part of a discussion meeting issue ‘Connectome to behaviour: modelling C. elegans at cellular resolution’.

1. Introduction

During the last three decades, extensive studies of Caenorhabditis elegans have provided wide-ranging data about the organism, including the most detailed connectome of any adult organism available to science. While the nervous system of C. elegans is the best mapped [1], nervous systems are intrinsically coupled to a body. Sensory neurons transform energy impinging on a body into neurochemical signals that yield information about the outside world. Similarly, motor neurons transform signals from the nervous system into activation patterns of muscles, which in turn create physical forces on a body and cause it to move through an environment. Therefore, our understanding of the way a nervous system coordinates behaviour is deeply tied to the ability to accurately account for the inputs and outputs to that nervous system [2]. One of the difficulties of modelling biological neural networks is verifying the output of a neuronal simulation without the corresponding constraints provided by the rest of the organism's body.

However, in recent years, a growing number of researchers see new hope in gaining a deeper understanding of the complete organism with the help of detailed computer simulations, including its body with sensory, nervous and muscular systems, and a subset of its environment [3]. Integrating a model of an organism's body, and in particular its muscular system, could enable a simulation to close the loop between sensory input, neural processing and the resultant action of the organism upon the environment around it.

A robotic system operating in the real world can be used in concert with a software simulation of a nervous system to show its behaviour (e.g. [4]). However, in the case of C. elegans, a tiny approximately 1 mm long nematode, creating physical robots is challenging. First of all, the expense of making a robotic system to the same scale would be significant. For this organism, scale is important because in order to reproduce the worm's natural habitat (soil in nature, agar in a Petri dish), one needs to take into account such physical effects as capillary force, surface tension, viscosity etc. Despite some recent progress in soft robotics [5,6], creating soft robots only a millimetre long with a sophisticated control system, would be very challenging. Larger physical scales (decimetre and more) that are already attainable by robotics systems [7] create significantly different relationships between capillary/surface tension/viscosity/gravity and other forces.

Biophysical measurements of the C. elegans worm body are some of the most comprehensive for any animal in the field of biology. Detailed measurements exist of swimming and crawling behaviour [8–10], elasticity [11,12], muscle force [13], frictional forces [14] and more. Data of this kind have been used as important validations for comparisons of biophysical computer simulation models built in the past (electronic supplementary material, table S1).

Software packages dealing with physical simulations of liquids, gels and their relationships with flexible elastic materials have been present for engineering applications for some time [15]. As a result, a fully software-based approach that enables the simulation of some well-characterized tissues and their relationship to liquid and gel environments present an attractive alternative to exploring the relationship between the body of an elastic organism in an environment and its control system when compared with physical robots.

The type of question that one wishes to ask of a model is crucial to determine the level of complexity to which the model should be built. Because C. elegans offers such a rich literature on the details of its biophysics and cellular anatomy [16], it is possible to ask detailed questions about the relationship of the motor system to the muscle system that can hinge on the activity of individual neurons or muscle cells. Given the goal of cells-to-behaviour-level understanding, representing the tissue surrounding muscle cells is an important consideration.

Here we present an application of the Sibernetic engine [17] that serves as a basis for key features of the simulated body of the C. elegans nematode. Three-dimensional (3D) models of both individual muscle cells and a whole C. elegans body are converted into a 3D particle system. Simulations are run to compare the mechanics of both the muscle cells and the body model to the real organism.

2. Methods

(a). Building blocks for a worm body

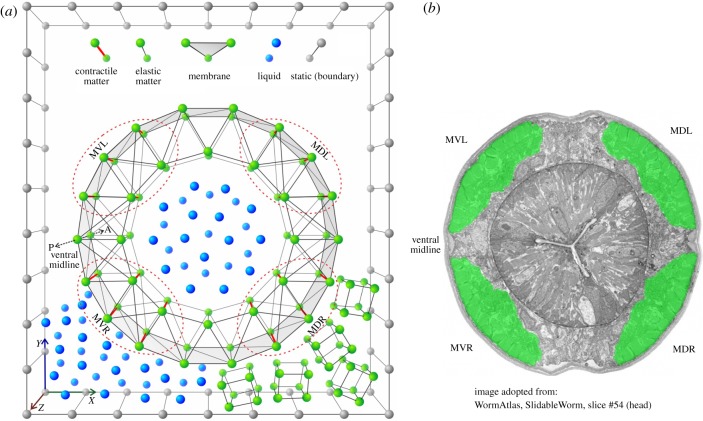
In a previous publication, we have described Sibernetic [17], an open-source finite particle simulation engine based on the Predictive Corrective Incompressible Smoothed Particle Hydrodynamics (PCISPH) algorithm [18] and extended to support novel matter relevant to biophysical simulation, such as the creation of elastic matter, contractile matter and membranes. Sibernetic enables complex geometries to be assembled from groups of particles. Figure 1 shows an example of assembling a simplified body segment from a worm-like body. The cross-section here shows the case where membranes are used on its outer surface. This enables the creation of a chamber within the cross section where liquid particles can be contained, while still keeping other liquid particles and gel-like elastic cube particles outside the cross section. The interactions between the liquid particles and the particles composing the membrane create pressure that causes the cross section to maintain its shape, much like the air inside a basketball.

Figure 1.

Construction of a cross section of C. elegans body model via particles (not to scale). At the top of (a) a legend for types of matter supported in Sibernetic [17]. Matter is represented as individual particles, or lattices composed of particles connected with springs. From basic components, multiple kinds of tissue can be constructed from different lattice configurations. (a, bottom) A cross section of the C. elegans worm body model, containing four quadrants of muscle cells highlighted with red dashed lines. Thick red lines within them represent contractile fibres of model muscle cells. This muscle cell example has contractile fibres along the Z-axis of the muscle, while it has elastic fibres in the X and Y directions of the muscle. Membranes make up the outer surface of the cross section. Liquid particles are depicted both inside the cross section, representing the liquid that creates internal hydrostatic pressure within the worm (electronic supplementary material, Methods 2.6), and outside the worm in the bottom left-hand corner, representing particles that make up the liquid (2.4) environment that the worm body model comes into contact with during swimming. In the bottom right-hand corner outside the worm are elastic cubes representing the gel-like environment used for crawling (2.3). Boundary particles define the outer limits of the simulation area. (b) The microphotograph of a real C. elegans cross section with corresponding labels for the muscle quadrants (reproduced with permission from WormAtlas [16]).

Another feature of the cross section in figure 1 are the embedded muscles within it. The cross section is composed of an outer ring and an inner ring. Between these two rings, there are four quadrants that contain contractile matter, much like what is shown in figure 1b. These four quadrants contain contractile matter that can squeeze the cross section in the Z-axis, and do so independently of one another. Along the X- and Y-axes are passive elastic matter connections, which demonstrates that the contractile matter can be constrained to pull along a specific axis if desired. Falling outside of the boundaries of the quadrants are also passive elastic matter connections.

With these building blocks, contractile matter was formed into approximations of muscle cells. A series of cross sections with internal liquid pressure and muscle cells embedded within them were unified into a body prototype of the invertebrate C. elegans (electronic supplementary material, Methods 2.5, 2.6). A computational interface enables the stimulation of arbitrary patterns of muscles (electronic supplementary material, Methods 2.7). A visualization system can be used to observe the model evolve in time (electronic supplementary material, Methods 2.8).

(b). Muscle cells

In C. elegans, 95 body-wall muscles are arranged in four quadrants as one observes the worm's body in cross section. Each muscle is rhomboid-shaped, and appears as staggered pairs. Looking within the muscles, they are striated by muscle filaments. These filaments lie inside the muscle membrane, and are attached to the exoskeleton/cuticle along the length of the cell.¹

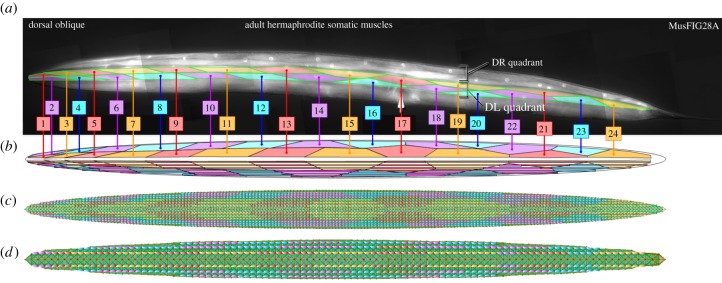
We mapped the anatomical features from C. elegans into our model within Sibernetic. The elastic shell is mapped into areas corresponding to four longitudinal muscle bundles, each located in its quadrant (VR, ventral right; VL, ventral left; DR, dorsal right; DL, dorsal left) (figure 1a; Q1–Q4), and every bundle is also mapped into 24 areas representing individual muscle cells with a geometry based on the microphotograph (figure 2).

Figure 2.

The mapping of muscles from WormAtlas (reproduced with permission from WormAtlas [16]),^8,9 (a) into readouts of their corresponding simulated muscle units in Sibernetic (b). High- (c) and low-resolution (d, twice lower) models are shown.

Muscle naming and enumeration from the DL side of the worm (figure 2) was used to create the geometries of the muscles. This pattern was copied and mirrored when necessary for the DR, VR and VL quadrants. While C. elegans lacks a muscle in one quadrant, we have left it in for symmetry purposes, but could remove it with minimal impact on the model.

Each ‘muscle cell’ includes 4–5 or more ‘muscle fibres’ (figure 1a). Every muscle ‘cell’ is composed of contractile matter with contractile fibres oriented in the anterior–posterior direction with some slope corresponding to body curvature at the head and tail ends.

Muscle fibres in the worm model are created by making some of the connections between the elastic matter particles in the shell into contractile connections (figure 1). The connections chosen are oriented along the length of the worm and are additionally located in one of four quadrants containing muscles in the real worm.

The frequencies of Ca²⁺-driven action potentials in C. elegans muscle determine its contraction. Action potentials are driven by graded motor neuron inputs, which typically consist of both excitatory cholinergic synapses and inhibitory GABA synapses. Muscle contraction is not all-or-nothing, and will create more force depending on the number and frequency of action potentials elicited in its membrane [19].

In the simulated system, we do not explicitly represent action potentials. Instead, the elastic force that acts on an ordinary elastic particle is

where k is a coefficient of elasticity, j is an index running through all particles forming elastic connections with elastic particle i, r_ij = r_i−r_j is a vector, connecting the i-th and j-th particles, and ‖r_ij‖ and 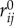are the current and relaxed-state lengths of elastic connections, respectively. If some particular pair of particles, i and j, is connected with a contractile matter (muscle) fibre, an additional force is applied to them:

where f_max is the maximal contraction force. C_corr is the muscle force correction coefficient (electronic supplementary material, Methods 2.7), which has a different function dependent upon the type of movement being simulated (swimming or crawling). u(i,j) is the position along the worm body of the cell that a given muscle fibre is contained within and takes values between 0 (head) and 1 (tail). a_ij^muscle is the total current activity of the muscle fibre, taking values between 0 and 1, caused by one or more activation signals from neurons or any other external source. All muscle fibres within the same cell share the same level of activity in the current model.

Maximal muscle contraction force was empirically found as a value which provides reasonable realistic bending. The maximal muscle contraction value as well as the functions for the muscle force correction coefficient were determined by testing. When the value of maximal muscle contraction is too weak, the worm does not bend very much. If the value is too large, the worm's shape becomes unrealistically curved. The chosen value of 2.7 × 10⁻⁹ N (electronic supplementary material, table S3) best reproduced typical worm geometries based on visual inspection, and, in addition, is in good agreement with the estimate of C. elegans muscular cell force, (1.4–9.6) × 10⁻⁹ N (electronic supplementary material, Methods 2.1).

(c). Reproducing a high-viscosity gel-like environment

The natural habitat of the worm is soil, and in a laboratory it usually lives in agar plates. ‘Agar’ is a gel-like elastic matter (a polymerized state of 2–5% agar solution), which is quite deformable as evidenced by the way a worm crawling over its plane surface leaves a groove in it. This should significantly influence the crawling process, as it allows a worm to push from its edges and thus locomote without sliding, slipping only along the groove and reducing lateral slipping.

To reproduce this process, different approaches were tried, among which were using a very viscous fluid, using a continuous plane pad of elastic matter with higher or lower elasticity and employing various regular (periodic) structures composed of elastic matter. Our current method uses an environment that behaves like an agar gel. We use small elastic matter cubes, each composed of eight particles, initially located in the nodes of a 3D grid with a space between adjacent cubes with 1.5–1.7 cube lengths, which form a pad on the ground. Its lowest layer is attached to floor, while the remaining 5–6 layers of cubes can freely move. After the beginning of the simulation they fall down forming the ‘agar’ layer.

(d). Reproducing a low-viscosity fully immersed water environment

Caenorhabditis elegans is capable of swimming through water and other low viscosity environments, using a significantly different gait than it uses during crawling. Therefore, it was important to reproduce the key aspects of the interactions between the worm's body and liquids in our environment.

We have designed a liquid environment with a viscosity ≈1.4 mPa s (electronic supplementary material, Methods 2.2, 2.4) that contains enough particles so that the model of C. elegans can be fully immersed. It consists of 500 K particles in a full-resolution model but only 81 K particles in a half-resolution model. The worm is put into a box partially filled with liquid, with a height between 100 and 200 µm, so the worm body may be completely immersed into it. At the start of the simulation, the worm body is oriented horizontally (ventral part on the left side and the dorsal part on the right), and located above the liquid surface. After initialization, the worm falls into the liquid and starts swimming. The amplitude of the periodic signal grows linearly from 0 to 1 until it reaches 1.

The density of the worm body is equal to the density of the outer liquid. The simulation starts with a configuration in which the worm is fully immersed in the liquid, right below its surface. We performed an additional in silico experiment, where the environment was filled with liquid at twice the height, and the positioning of the worm's body halfway between the surface and the bottom of the liquid was observed again. Soon after the simulation starts and the worm starts moving, the worm descends so that its body is positioned halfway between the surface of the liquid and the bottom of the environment and continues swimming at this position (electronic supplementary material, figure S5).

It has been noted that C. elegans swimming is subject to the counterintuitive properties of ‘low-Reynolds number environments' as a result of their small scale [20,21]. This leads to some physical dynamics that are different from other swimming animals, such as the Lamprey. The key difference is that inertial forces at low-Reynolds number are far outweighed by viscous forces, making the progress of a swimming undulatory animal stop immediately when it stops moving. In high-Reynolds environments, inertia operates at a much larger extent by carrying the animal forward for a small distance, even after it stops moving. We wanted to ensure that our liquid environment was within a related low-Reynolds number regime, so we calculated the Reynolds number in this environment to be less than or equal to 0.05 (electronic supplementary material, Methods 2.3, 2.4) for the case of worm swimming.

In addition, surface tension was implemented as per ([22], §3.3).

3. Results

In this section, we describe results from several in silico tests conducted to verify the assemblage of simulated tissue material, from a straightforward verification of friction, to the testing of more complex geometries with multiple particle matter types. We describe the performance of simulated muscle cells with respect to known properties of real muscle cells, and finally compare the worm body simulation dynamics to those measured in biophysical experiments.

(a). Individual muscle cells

We created a separate test that focused on the contraction and relaxation of our simulated muscle tissue (electronic supplementary material, Methods 2.1). This test also enables us to measure the contraction force empirically. Our test had a cross section of the worm's body that included all four muscle quadrants and was attached to the ceiling of the test environment. This allowed the section to be pulled downwards by gravity forces.

We used the test set-up (see electronic supplementary material, figure S1) to make several measurements of the dynamics of our simulated muscle tissue to compare it against other models and against what is known about real C. elegans muscle tissue and muscle tissue in general (figure 3). In measurements of velocity versus force, we found a characteristic nonlinear relationship that is well known in muscle physiology (e.g. [23]). In measurements of force versus length, we compared our results to the model of [24] to demonstrate both the consistency to this previously reported model, but also the additional noise introduced by our particle-based approach.

Figure 3.

(a) Velocity versus force for the muscle test, for different values of muscle strength, taken as a fraction of the maximal muscle strength (2.7 × 10⁻⁹ N; also see electronic supplementary material, table S2 and Methods 3.1). Tests were conducted by applying the force and measuring the velocity with which the muscle contracted (b) Force/length relationship obtained by holding the muscle at a specific length (X-axis) and measuring the force needed to keep the muscle at that length (Y-axis) for different values of muscle strength, as in a. Figure on the left is from Boyle et al. [24] (Reproduced with permission by Netta Cohen). Figure on the right shows measurements from our muscle test.

(b). Reproducing basic movements

After testing muscles and sections of the simulated body, we created tests built around a complete C. elegans body model. Basic behaviours such as assuming an omega-turn posture, shortening (figure 4) and reproducing two-frequency undulation (figure 6) were reproduced. Using a computational interface to stimulate specific muscles (electronic supplementary material, Methods 2.7), we aimed to reproduce very simple postures.

Figure 4.

Two basic behaviours exhibited in C. elegans reproduced by Sibernetic, shown via the visualization system (electronic supplementary material, Methods 2.8). (a) Sibernetic reproduces an omega turn posture.¹⁰ (b) Sibernetic reproduces a shortening behaviour.¹¹

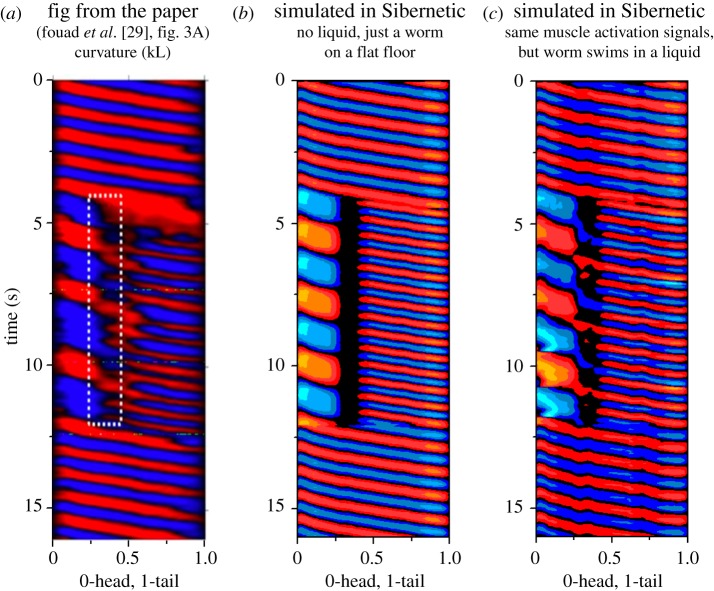
Figure 6.

A set of three curvature graphs demonstrate the swimming behaviour of the body model being interrupted by ceasing to send modulation input into the muscles in the worm's ‘neck’. Two frequencies of crawling occur in this case, which is known as ‘two-frequency undulation’. (a) Shows real data from a worm whose neck muscles were experimentally inactivated (reproduced with permission from Fouad et al. [29]), (b) shows results from Sibernetic without a liquid substrate and (c) shows results from Sibernetic within a liquid.

Caenorhabditis elegans has a well-known omega-turn posture where it contracts muscles on one side only. To reproduce this behaviour, we addressed the dorsal muscles on the right and left sides of the model's body and caused them to contract. Figure 4a demonstrates the final posture assumed by the body model after this contraction took place.

Strains of C. elegans that have muscle cells with greater than average contraction often have the ‘shortening’ phenotype. To investigate if Sibernetic could reproduce this, we sent equal activation force to all muscles between the tail and the head. As shown in figure 4b, we observed the worm reducing its length and increasing its width in a characteristic manner observed in the real organism.

(c). Swimming and crawling

To compare the performance of Sibernetic to that of real C. elegans, we generated experimental scenes within Sibernetic with equivalent environmental conditions to what were reported in experimental papers [25–27], as well as what we measured from videos depicting C. elegans in crawling² and swimming³ behaviours. We used a computational interface to inject different behavioural patterns into the simulated muscle cells corresponding to swimming and crawling (electronic supplementary material, Methods 2.7). We chose some behavioural patterns with frequencies that were both very near each other and also further apart in both swimming and crawling conditions to test the simulations' robustness to small and large perturbations (table 1).

Table 1.

Locomotion (crawling and swimming) characteristics.

	experimental measurements	Sibernetic simulations
velocity (mm s−1)
crawling over a surface with a gel (10–100 mPa s)	0.1–0.3 [27] 0.19 (forward)/0.3 (backward) (crawling video)	0.13–0.15
swimming in a water-like low-viscosity liquid (approx. 1 mPa s)	0.29 ± 0.03 [7] 0.38 ± 0.02 [26] 0.29–0.38 (swimming video)	0.26–0.41
wavelength (λ/L, where L is the length of the worm)
crawling over a surface with ‘high viscosity' (10–100 mPa s)	0.65 ± 0.03 [25], 0.48 (crawling video)	0.57–0.85
swimming in a water-like low-viscosity liquid (approx. 1 mPa s)	1.54 ± 0.04 [25] 2.15 ± 0.07 [26] 1.54 (swimming video)	1.49–1.66
frequency (Hz)
crawling over a surface with ‘high viscosity’ (10–100 mPa s)	0.3 ± 0.02 [25] 0.30–0.49 (crawling video)	0.27–0.41
swimming in a water-like low-viscosity liquid (approx. 1 mPa s)	1.76 ± 0.07 [25] 1.99 ± 0.05 [26] 1.76 (swimming video)	1.75–1.79

In figure 5, we show our results from frequency and wavelength measurements from Sibernetic experiments for the cases of swimming⁴ and crawling.⁵ This is comparable to those in [28], figure 1a, with the best fit line having a slope of 0.59 and an intercept of 0.48 ([28] slope: 0.64, intercept 0.42). In addition, an ability of simulating swimming and crawling within the single scene was demonstrated,⁶ as well as crawling forwards followed by a reverse.⁷

Figure 5.

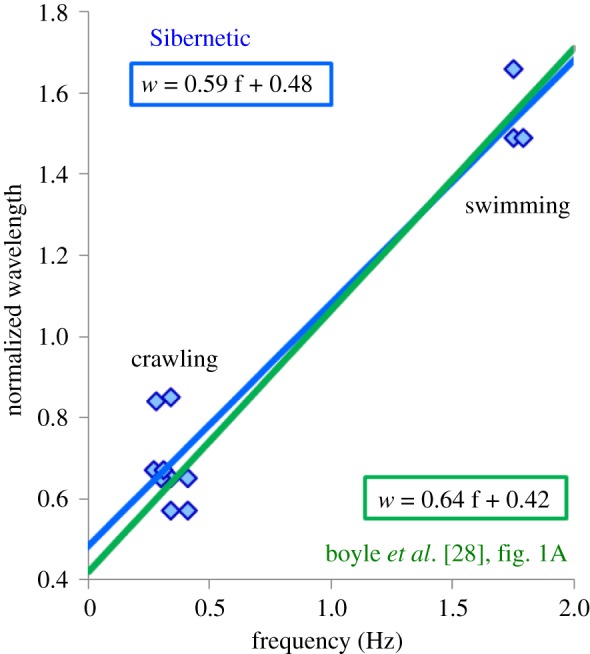
Reproducing frequency and wavelength for swimming and crawling.

When the muscles are activated, force is propagated throughout the connections between the particles to ultimately create movement in the entire worm body structure. This has the effect of moving the cuticle through the medium that it is within. In the case of simulating agar, the force enables the worm to create forward motion by forming a groove. As the groove forms, forces that are in parallel with the worm create forward motion as the cuticle interacts with the formed groove. In the case of simulated liquid, the worm is immersed in a chamber whose height is taller than the largest diameter of the worm body. In this case, the forward motion is created in a similar manner to the agar, but instead of a more viscous groove, the interaction between the cuticle and the liquid create the forward force.

(d). Reproducing two-frequency undulation

Fouad et al. [29] demonstrated, through optogenetic inactivation of neck muscles among other methods, that C. elegans is capable of producing different undulatory frequencies in different parts of its body, as if we had the ability to optogenetically stimulate each muscle cell independently. To explore the biomechanics of two-frequency undulation, we gave Sibernetic a set of patterned inputs (electronic supplementary material, Methods 2.7) that began with sinusoids capable of producing a single undulatory frequency, and then simulated the inactivation of neck muscle cells by removing input from them. Simultaneously, we fed two different frequencies to the head and tail sections during the neck inactivation period. Following a brief time period, we restored the original muscle activation pattern. Figure 6 shows the results.

4. Discussion

In this paper, we have demonstrated in silico modelling of muscle cells, elastic tissue, cuticle and environmental interactions of C. elegans using the open-source Sibernetic PCISPH engine. The model has properties such as internal hydrostatic pressure, 96 independently activable body-wall muscles, whose properties integrate experimental observations of real muscle force and structure, the ability to reproduce postures observed in the real worm, such as omega turns and shortening, and forward locomotion capacity (swimming and crawling) at speeds comparable to the real organism. Changes in shape of the worm body (e.g. figure 4b) are especially difficult to reproduce in models that do not explicitly represent a cuticle that has elastic properties. The model can also reproduce idiosyncratic behaviour such as two-frequency undulation, which relies on being able to modulate specific sets of muscle cells to affect overall behaviour.

It is also fully open-source, available for inspection and use by the broader scientific community. While there are still many mechanical properties left to simulate about C. elegans, we believe this represents the most detailed biomechanical simulation of C. elegans developed to date.

Our model of individual muscles was compared against the existing output of the simulated muscles in the 2D model of [24] and returned comparable results that included additional noise. A difference in the scales of muscle force between the two models (figure 3b) relates to the use of different references chosen for the calculation of the real C. elegans' muscle strength (electronic supplementary material, Methods 2.1). Because the muscles themselves are not a linear dynamic system, we believe that these additional nonlinearities add additional biological realism to the model we have implemented in Sibernetic. As a result, it creates additional challenges for a control system to deal with, which in turn creates a higher standard for the output of a neuronal system to meet to be comparable to the real animal.

Previous work has investigated the use of rigid-body simulations of the C. elegans body (electronic supplementary material, table S1). Our own previous investigation took the form of the CyberElegans simulator [30]. Muscles were represented only as a spring between two point masses. The rigid-body simulation therefore allowed only for the creation of a rigid ‘cross-beam’ structure for the worm. Swimming was not simulated because the surrounding liquid environment could not be incorporated. AnimatLab [31] is an open-source neuromechanical simulation tool that is a general purpose system for simulating embodied agents. Its goal is to enable exploration of the relationships between model nervous system activities and environments. It can simulate biologically reasonable neurons, muscles, sensors, organisms and their environments, including minimal support of liquid simulation—a volume of a given height and density can be included into simulation, with forces of buoyancy and drag acting on the objects within the volume. However, this is substantially not enough for C. elegans swimming simulation. Cohen & Ranner [32] offer a novel method for calculating a rigid 2D or 3D cylindrical shell for a worm body that has four orders of magnitude fewer degrees of freedom than this method and can take on a variety of worm poses. However, within this approach, crawling is rather modelled as swimming within a continuous highly viscous liquid, as crawling over the surface of a gel and formation of a groove in it are not considered.

In contrast with rigid-body simulations such as CyberElegans, AnimatLab or Cohen & Ranner [32], the PCISPH approach we describe in this manuscript has several advantages, which stems from our decision to capture the physical aspects of biological tissue in our model. There is a significant literature on the biophysical properties of the body of C. elegans, estimating parameters such as stiffness based on muscle tension versus hydrostatic pressure on the cuticle [33] or the Young's modulus of the worm's shell [11], and many others that demonstrate results from experiments with the physical 3D body of C. elegans. These observations can only be fully reconciled with each other and integrated together via a modelling system in which the biomechanical experiments conducted on C. elegans bodies can be conducted on the model and compared. As a result, a model that captures the 3D anatomical, structural and biomechanical properties of the tissue of the C. elegans body will have an additional ability to synthesize these results in a way that models that are less detailed cannot.

Additionally, in contrast with a rigid-body approach, it enables both fluid and soft bodies to be simulated and to interact. Using an SPH-based approach, increasing the resolution of material (liquid, elastic etc.) is a simpler and more automated process. It is possible to measure values such as pressure and force in the SPH-based simulation more easily by using particles as ‘tracking particles’. This is used for measuring values such as hydrostatic pressure in the worm cavity (electronic supplementary material, Methods 2.4). The SPH approach, with its ability to use many particles to create curved surfaces, allows for the flexibility to make the worm body match anatomical features with greater precision.

Previously there has been no computational way to deeply study worm swimming. Take the case of the swimming behaviour in C. elegans. It has been well studied biomechanically [25]. As the worm swims, the surface of the liquid it is swimming in completely encases it. As it moves through that liquid, differential pressure on one side of the worm increases relative to the other side. In addition, in our investigations, the movement through liquid creates complex flows around the body of the worm that would be difficult to capture with a simple linear model of the physics of the environment. No other model of C. elegans has included an explicit liquid model with a body model (electronic supplementary material, table S1), and therefore previously there has been no computational way to deeply study worm swimming.

Another important aspect of the modelling done here in three dimensions is the advantage of having a three-dimensional spatial representation of the volume of the muscles. Because the muscle cells occupy space within the body of the model, additional aspects of the relationship between muscle physiology and body dynamics can be explored. A much more accurate mapping of microscopy data surrounding the anatomy of the muscle cells can be incorporated. For example, real muscles in C. elegans will change their shape when they contract [19], which in turn affects the shape of the body they are inside (e.g. figure 4b). Another example is that real muscles in C. elegans are attached to each other and to the body wall in specific ways via their sarcomere assembly [34], which can only be appropriately captured in three dimensions. The range of motion of the model we have built is also important. A three-dimensional body enables three-dimensional range of motion. In nature, C. elegans lives and behaves not in a two-dimensional flat land but burrows through soil in three dimensions. Its musculature is therefore capable of producing motion in all three directions, especially its neck muscles.

There are some considerations of this approach that are disadvantages compared to models with lower complexity. One is that the particle system simulation is more computationally expensive than two-dimensional dynamical systems, and therefore run more slowly on the same hardware. Additionally, the higher complexity means that it takes more time to iterate the model and it is more complicated to learn how it works. Finally, it is possible that the explanations for the behaviours that emerge from the model may be more complicated, and therefore take more time or analysis work to understand. These considerations, in our view, however, are not reasons to not build a more comprehensive model, but they are worthy reasons to potentially begin ones' questions with simpler models first, and later convert those questions into models like the one in Sibernetic for deeper investigation.

Therefore, the approach of building a physical simulation at this level of detail provides an effective framework to deeply constrain the activity of the C. elegans nervous system within a closed loop system of a body and an environment. By assembling this model from a combination of constraints given by biophysical measurements of the tissue, we have learned that if we define the correct frequency and wavelength of the worm body along with the correct viscosity of a liquid or gel environment, we can get a crawling and swimming velocity which is very close to that for a real worm at the same conditions. Because the model enables behavioural output that is strongly comparable to real behaviour, we offer that this model provides a more efficient way to reduce the space of uncertainty about how the biomechanics of C. elegans could work compared to other means of reasoning about the aggregate effects of the biomechanics, e.g. simple logic or back-of-the-envelope calculations. In turn, we can explore the space of possibilities of how different patterns of muscle activation affect behaviour, which in turn allows users of this model to explore the space of possibilities of how different patterns of nervous system activity affect behaviour. For the first time, this enables an approach to generate new hypotheses with greater biological specificity about the internal state of the C. elegans neurons and body-wall muscles relative to its body posture and the forces acting on it. This provides a foundation to seek dynamical principles that hold within the complex biophysical interactions between the activity of the cells of the nervous system, muscular system and outside environment of a living organism.

(a). Future work

The approach we have taken here of using a more detailed and computationally complex means of simulating the biophysics of C. elegans has been done in order to enable a significant amount of additional measurements, observations and anatomical data to be integrated into the same model. The most obvious next step is to show the results of incorporating an electrical model of neurons and muscles together, such that stimulating motor neurons causes stimulation of muscle cells, and the electrical activity of the muscle cells can be related to the contraction/relaxation force within Sibernetic.

In addition to motor neuron activity, different kinds of sensory input can also be incorporated into the particle-based model. Mechanosensors, in particular, is a focus for our next effort. Our approach provides the ability to use corresponding points of the simulated C. elegans body for providing input data for the sensory system, especially mechanosensory. While some recent 2D models have incorporated proprioception [35], this has been captured purely as a matter of the posture of the worm's body, whereas here we have the ability to also simulate gentle touch or harsh touch on any point along the 3D surface area of the worm's cuticle. This would enable studies that show the effect of modified neuronal properties (by mutation, drug interaction, etc.) that lead to quantifiable behavioural differences to be modelled within Sibernetic (e.g. [36]). Including other kinds of sensory input such as thermosensors, by incorporating temperature as a property of each particle, or photosensors and chemosensors in a similar manner would be straightforward. Finally, in order to achieve simulation of peptides diffusing through the body of the worm, a 3D volume in which to do this would enable diffusion–reaction models to operate such that the spatio-temporal nature of these dynamics would have a more realistic backdrop on which to operate.

Because the particles draw a direct analogy to tissue that has mass and takes up 3D space, we can continue incorporating additional anatomical features of C. elegans within the same simulation framework. For example, adding a pharynx to the front of the worm with muscles that pump in the way that the real pharynx does would be straightforward. By updating the model to have muscles in the head of the worm that are organized as a pharynx, we could now compare pharynx pumping data to what happens in our worm. Similarly, egg-laying or defecation could be incorporated by the addition of vulval and anal muscles and pores. To incorporate these features into simpler models, significant changes to the fundamental architecture of the model would need to be made. In Sibernetic, these updates are simply a matter of adding or modifying the appropriate relationships between key particles within the volume of our model.

Data accessibility

The Sibernetic software [17] is free, open-source, able to run on Linux, Windows and MacOS operating systems and is available at sibernetic.org or https://github.com/openworm/sibernetic along with all necessary data files.

Authors' contributions

A.P. and S.L. drafted the article with S.K. revising it critically for important intellectual content. A.P. and S.K. wrote all code associated with the underlying system. A.P. focused on the scientific measurements and programming, while S.K. focused on infrastructural and computational aspects of the code.

Competing interests

We have no competing interests.

Funding

The work of A. Palyanov and S. Khayrulin was partially supported by Russian Foundation for Basic Research grant no. 18-07-00903 and by Russian Ministry of Science and Education under 5–100 Excellence Programme.