Comparison of in vitro and in vivo clastogenic potency based on benchmark dose analysis of flow cytometric micronucleus data

Abstract

The application of flow cytometry as a scoring platform for both in vivo and in vitro micronucleus (MN) studies has enabled the efficient generation of high quality datasets suitable for comprehensive assessment of dose–response. Using this information, it is possible to obtain precise estimates of the clastogenic potency of chemicals. We illustrate this by estimating the in vivo and the in vitro potencies of seven model clastogenic agents (melphalan, chlorambucil, thiotepa, 1,3-propane sultone, hydroxyurea, azathioprine and methyl methanesulfonate) by deriving BMDs using freely available BMD software (PROAST). After exposing male rats for 3 days with up to nine dose levels of each individual chemical, peripheral blood samples were collected on Day 4. These chemicals were also evaluated for in vitro MN induction by treating TK6 cells with up to 20 concentrations in quadruplicate. In vitro MN frequencies were determined via flow cytometry using a 96-well plate autosampler. The estimated in vitro and in vivo BMDs were found to correlate to each other. The correlation showed considerable scatter, as may be expected given the complexity of the whole animal model versus the simplicity of the cell culture system. Even so, the existence of the correlation suggests that information on the clastogenic potency of a compound can be derived from either whole animal studies or cell culture-based models of chromosomal damage. We also show that the choice of the benchmark response, i.e. the effect size associated with the BMD, is not essential in establishing the correlation between both systems. Our results support the concept that datasets derived from comprehensive genotoxicity studies can provide quantitative dose–response metrics. Such investigational studies, when supported by additional data, might then contribute directly to product safety investigations, regulatory decision-making and human risk assessment.

Introduction

There is growing recognition that quantitative approaches for dose–response analysis and risk assessment that are commonly employed in other fields of toxicology have the potential to serve important roles in genetic toxicology (1–3). The premise that genotoxicity data are not only useful for determining hazard, but can also contribute directly towards broader risk-based decision making, has reinforced the need for more comprehensive and informative means of interpreting and using genotoxicity data. Thus, the application of point of departure (PoD) analyses to genetic toxicology data has recently received increasing attention. Looking beyond the simple categorisation of a compound as ‘hazardous’ and making more than a ‘yes/no genotoxicity call’ is the rationale for developing new quantitative methods in order to make the best use of existing data.

This topic has been the focus of several industry working groups and their observations and recommendations were summarised in several recent publications. Gollapudi et al. (4) described BMD, threshold effect level (Td) and the ‘no observed genotoxic effect level’ (NOGEL) as potential approaches of evaluating quantitative dose–response information from genetic toxicology studies. In a follow-up report, Johnson et al. (5) focussed on specific examples for the application of these PoD metrics as a means to assess the merits and limitations of existing methods and guide the use of these tools for generation of reference doses, margins of exposure, etc. Slob and Setzer (6) conducted an analysis of several different toxicology study formats including subchronic toxicity, local lymph node assay, in vivo and in vitro micronucleus (MN), whole embryo culture developmental assessment, etc. in order to examine the shape of toxicological dose–response relationships. They concluded that the dose–response curves all shared a similar shape despite being derived from very different assay systems. The authors went further to state that ‘the finding that the choice of the dose–response model is not crucial may help convincing toxicologists and risk assessors who have difficulty in accepting the BMD approach’.

Finally, at the 2013 International Workshops on Genotoxicity Testing (IWGT) held in Foz do Iguacu, Brazil, the Working Group on Quantitative Approaches to Genetic Toxicology Risk Assessment (QWG) reviewed the current status of PoD metrics and described consensus statements and future needs for genetic toxicology (2,3). One of their conclusions was that the preferred method of dose–response analysis is determination of the BMD, as this approach is used regularly in other risk assessment contexts and it makes use of all available data. The QWG also stated that no matter what quantitative approach is used, ‘there is a need for high quality data’, and any uncertainties that may exist based on the data and chosen approach should be clearly represented. Evaluation of the uncertainties in relatively poor datasets may benefit from robust dose–response estimates derived from studies that include broad dose ranges and sufficient sample size.

Our laboratory has developed methodologies for flow cytometric assessment of MN formation in both in vivo and in vitro systems. These methods share characteristics such as simple, efficient sample processing, automated, objective scoring and high throughput sample analysis that can generate data in minutes or even seconds per sample. Thus, high quality data can be practically and efficiently obtained via these methods. Given the established qualitative role that these assays already serve in genetic toxicology, for example hazard identification, expanding their quantitative utility by examining the relationships that may exist between both test systems is an important pursuit.

Based on examples in the literature and recommendations from the QWG, we applied BMD analyses to datasets obtained from several previously reported in vivo rat studies (7–9) and compared them to results obtained from new in vitro experiments with the same chemicals. Thus, these studies were focused on the chromosomal damage effects of seven well-known clastogenic agents representing diverse chemical classes: melphalan (MEL), chlorambucil (CHL), thiotepa (THI), methyl methanesulfonate (MMS), azathioprine (AZA), hydroxyurea (HU) and 1,3-propane sultone (PRS). These particular in vivo studies/chemicals were also chosen based on characteristics that seemed advantageous for the in vitro versus in vivo comparison—consistent rodent model, age, sex, treatment schedule/harvest schedule and consideration of multiple dose levels. The flow cytometric methodologies employed for both the in vivo and in vitro studies enabled very efficient collection of MN induction data across a large dose range of the study compounds. The resulting data were statistically analysed by fitting dose–response models and estimating BMDs (equipotent doses) in either test system. Further, we investigated the existence of a correlation between both systems, as well as the impact of the BMR (the effect size associated with the BMD) on that comparison.

Materials and methods

Reagents and test chemicals

MEL (CAS no 148-82-3), CHL (CAS no 305-03-3), THI (CAS no 52-24-4), MMS (CAS no 66-27-3), AZA (CAS no 446-86-6), HU (CAS no 127-07-1), PRS (CAS no 1120-71-4) were purchased from Sigma–Aldrich (St. Louis, MO, USA). Reagents for processing and analysis of peripheral blood samples for micronucleated reticulocytes were from In Vivo MicroFlow® Rat PLUS kits (Litron Laboratories, Rochester, NY USA). Reagents for staining and lysing cultured cells for MN analysis were from In Vitro MicroFlow® kits (Litron Laboratories).

In vivo micronucleus

Data from these studies were originally published across several papers that describe the development and validation of an in vivo gene mutation assay (7–9). All animal experiments were conducted with the oversight of the University of Rochester’s Institutional Animal Care and Use Committee. Male Sprague-Dawley rats obtained from Charles River Laboratories (Wilmington, MA, USA) were ~7 weeks old at the time of initiation of exposure. Test articles were administered via oral gavage at 10ml/kg body weight/day at ~24h intervals for 3 consecutive days.

The concentrations examined were based on preliminary dose-range information and were selected in order to achieve certain target exposures. The highest concentration tested was designed to achieve maximum tolerated dose (MTD) as defined by body weight and other indices of health. Other concentrations were selected based on variations of the numerical measure of carcinogenic potency (TD₅₀) as reported by the Carcinogenic Potency Database (10,11). In particular, we examined doses equivalent to 0.33 TD₅₀, TD₅₀ and 3× TD₅₀. These dose ranges allowed us to examine data from exposures that elicited dose-related elevations in peripheral blood MN-RET frequencies at low to moderate bone marrow toxicity, up to highly-induced responses observed at MTD.

On study Day 4, peripheral blood was collected via tail vein from five to six animals per exposure group for all studies. Fixation, processing and analysis of peripheral blood samples for MN-RET was performed according to the In Vivo MicroFlow instruction manual and as described elsewhere (12,13). MN-RET and RET frequencies were determined via analysis of ~20000 RETs per sample. The identification of the RET population was accomplished by staining the samples with a fluorescently-labelled CD71 (transferrin receptor) antibody and enumerating RETs by their elevated expression of this cell surface marker. All analyses were performed on a BD FACSCalibur™ flow cytometer running CellQuest™ Pro v5.2.

In vitro micronucleus

Human lymphoblastoid TK6 cells (American Type Culture Collection, Manassas, VA, USA) were maintained in RPMI 1640 medium supplemented with 10% horse serum, 200 µg/ml sodium pyruvate, 2mM l-glutamine, 50 units/ml penicillin and 50 µg/ml streptomycin. Medium and serum was obtained from Mediatech (Manassas, VA, USA), all other cell culture reagents were supplied by Sigma–Aldrich. Cells were continuously passed at less than 1.0×10⁶ cells per millilitre in a 37°C, humid atmosphere with 5% CO₂.

All TK6 cell treatments, processing and analyses were performed in 96-well plates as described in the In Vitro MicroFlow manual and elsewhere (14,15). Briefly, stock solutions of test article in dimethyl sulfoxide (DMSO) were serially diluted across wells containing fresh culture medium. Initial top concentrations of the various test articles were determined by preliminary dose-range finder experiments and the dilution series achieved up to 20 exposure conditions. Cells were then distributed across the plate and incubated for ~24 continuous hours in order to achieve the desired population doublings. Samples were analysed using a Becton Dickinson FACSCANTO™ II flow cytometer equipped with a high throughput sampler and running BD FACSDiva™ software. A total of four separate wells were analysed per treatment condition with a maximum of 10000 healthy cells’ nuclei evaluated per well.

Criteria for a valid in vitro MN assay included demonstration of 1.5–2.0 population doublings in vehicle-exposed control cultures that also showed baseline MN frequencies within the historical control distribution. Concurrent positive control MN values also needed to fall within the historical distribution. In addition to these criteria for assay validity, the conditions for selecting an acceptable top concentration for analysis were defined as exposures that achieved 50±5% cytotoxicity and had a %ethidium monoazide (EMA) positive events value <4-fold over solvent control. Data from concentrations that exceeded these culture viability criteria were not included in the BMD analyses.

Statistical analyses

Individual sample data were initially compiled in Microsoft Excel and converted to text files for input into PROAST software (RIVM, The Netherlands; www.proast.nl) operating in the R environment (16). The PROAST software allows for fitting a single dose–response model to combined datasets (relating to different subgroups), thereby establishing which parameters in the model differ significantly among the subgroups. Parameters that are not found to differ significantly will be estimated as a single value in the final model, while those parameters that do differ significantly are estimated as subgroup-specific values. This approach was followed for each test system, that is in vivo or in vitro MN, by combining the data for all chemicals and by fitting the dose–response model using chemical identity as a covariate (17). Critical effect sizes (CES) of 0.05, 0.5, 1, 2 and 4 were chosen to provide information on the BMD values at various points along the dose–response curves. CES is equivalent to BMR when defined as a percent change in mean response compared with the control baseline, thus the latter term will be used for the remainder of the manuscript. BMDs and their associated confidence intervals for each compound were obtained, these values were then used to rank compounds as well as examine the relationship between the test systems. Chemicals with non-overlapping confidence intervals can be differentiated from each other based on potency, whereas those with overlap cannot be ranked. The latter is an inconclusive result, unless the confidence intervals are deemed small enough to consider the chemicals as equally potent from a practical point of view. A more detailed description of the statistical methods can be found in Soeteman-Hernández et al. (18).

Correlation plots

The chemicals selected for this study were known to be potent clastogens, and the combined MN studies resulted in the ability to examine many doses. As a result, the BMD confidence intervals in this investigation were relatively small. In other cases, where BMDs must be estimated from smaller datasets, or when weakly potent or ‘non-potent’ chemicals are included, the BMD confidence intervals are wider, while they also partly have infinite upper bounds. In those cases, a correlation coefficient cannot be calculated, and another (visual) approach of evaluating the correlation has been used. We follow that visual approach here as well, for reasons of consistency. The approach is to draw two lines in the double-log plot with unity slope. A unity slope in a double-log plot translates into a proportional relationship between the BMDs on the original x- and y-axis. The two lines are drawn such that they encompass most of the BMD intervals. If the different chemicals scatter randomly between both lines, this indicates that the BMDs in both systems are proportionally related. The vertical distance between both lines reflects the uncertainty range of the predicted BMD on the y-axis, given a BMD on the x-axis. This uncertainty range can be regarded as a measure of the correlation (small range means good correlation). See L. G. Soeteman-Hernández, M. D. Fellows, G. E. Johnson, W. Slob (submitted to Tox. Sci.) for a more extensive discussion and an illustrative example how to use the two sloped lines in predicting the BMD on the y-axis.

Results

In vivo micronucleus

Fitting a four-parameter exponential model to the combined dataset (with chemicals as subgroups) showed significant differences among the subgroups regarding the potency parameter and the within-group variance, but not in background response. Therefore, the data were described by a four-parameter exponential model (6) with constant background and shape parameters, but with potency and within-group variance depending on the subgroup (chemical). The in vivo MN data and the associated curves generated by the model just mentioned are shown in Figure 1. The same data and curves are plotted in supplementary Figure S1, available at Mutagenesis Online, but now for each chemical separately. Based on visual inspection of the fitted curve for each individual chemical the overall conclusion is that all seven dose–response relationships can be described by the four-parameter exponential model, while assuming their shapes are the same. Figure 1 also shows the chemical-specific BMDs associated with a 3-fold induction from baseline (BMR = 200%). This response value was chosen here to more readily display the graphical representation of the derived BMDs. The horizontal line represents the chosen response value from baseline which intersects the dose–response curve and then drops down as a vertical line to the BMD on the x-axis. As described in the Statistical analysis, BMDs were also calculated for a number of other BMR values (supplementary Figure S2, available at Mutagenesis Online). Table 1 shows the BMD, and the lower (BMDL) and upper (BMDU) confidence bounds associated with various values of BMR.

Figure 1.

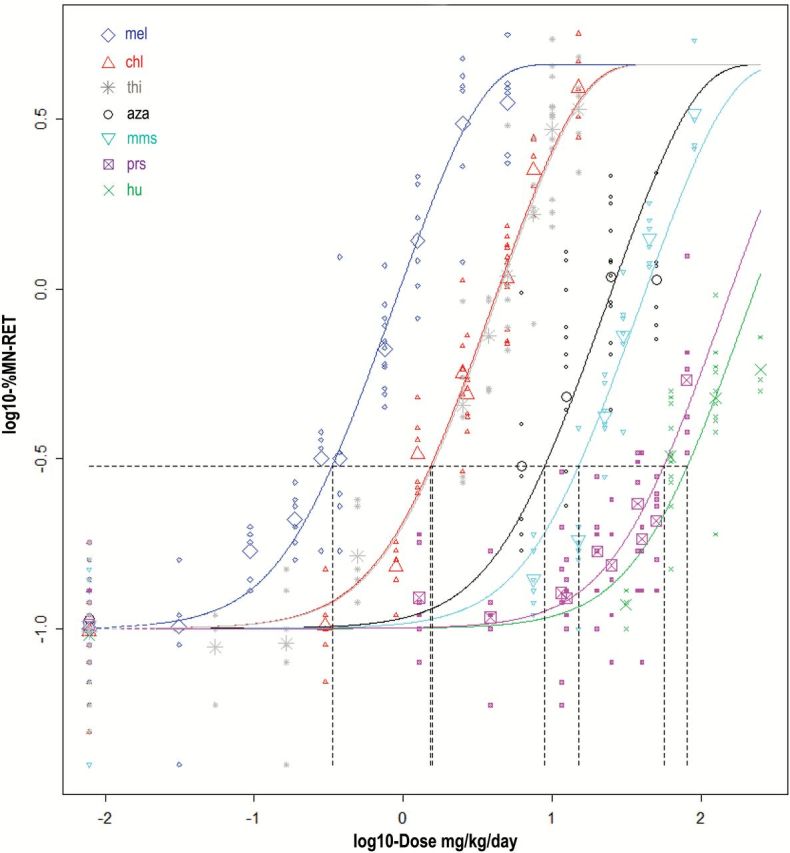
Fitted curves for in vivo MN dose–response data from seven clastogens studied in rats. The horizontal-to-vertical dashed lines represent the BMD concentrations that correspond to a BMR = 200%, that is a 3-fold induction of MN (=distance of 0.48 on log10-scale). For each chemical, the small symbols represent the individual data points and the large symbol represents the geometric mean of these observations.

Table 1.

BMD values for in vivo MN assay across varying BMR (units are mg/kg/day)

	AZA	CHL	HU	MEL	MMS	PRS	THI	Geometric mean
BMR = 0.05
BMD	0.7717	0.1325	7.0082	0.0289	1.3037	4.8628	0.1365
BMDL	0.5636	0.0991	5.3371	0.0218	0.9724	3.7600	0.0994
BMDU	1.0340	0.1725	9.0255	0.0376	1.6952	6.1718	0.1826
BMDU/BMDL	1.83	1.74	1.69	1.73	1.74	1.64	1.84	1.74
BMR = 0.5
BMD	3.5334	0.6066	32.0880	0.1323	5.9693	22.2650	0.6252
BMDL	2.8488	0.5114	27.1340	0.1113	4.9824	18.9060	0.5115
BMDU	4.3516	0.7105	37.8160	0.1562	7.0295	26.1750	0.7538
BMDU/BMDL	1.53	1.39	1.39	1.40	1.41	1.38	1.47	1.43
BMR = 1
BMD	5.6013	0.9616	50.8680	0.2098	9.4629	35.2960	0.9911
BMDL	4.6174	0.8374	44.0240	0.1812	8.1262	30.5020	0.8366
BMDU	6.7700	1.0947	58.8130	0.2416	10.8770	40.9870	1.1621
BMDU/BMDL	1.47	1.31	1.34	1.33	1.34	1.34	1.39	1.36
BMR = 2
BMD	8.9140	1.5303	80.9520	0.3338	15.0590	56.1700	1.5772
BMDL	7.4696	1.3704	71.1550	0.2946	13.2360	48.9930	1.3682
BMDU	10.6250	1.6998	92.4370	0.3773	16.9930	64.9410	1.8042
BMDU/BMDL	1.42	1.24	1.30	1.28	1.28	1.33	1.32	1.31
BMR = 4
BMD	14.3010	2.4551	129.8800	0.5356	24.1610	90.1180	2.5304
BMDL	12.0990	2.2438	114.8300	0.4789	21.5650	78.5950	2.2427
BMDU	16.9120	2.6800	147.7100	0.5987	27.0010	104.6100	2.8385
BMDU/BMDL	1.40	1.19	1.29	1.25	1.25	1.33	1.27	1.28

In vitro micronucleus

All of the chemicals studied showed dose-related elevations of MN indicative of chromosomal damage in vitro. Figure 2 shows the dose–response plot with the BMDs for each chemical, again corresponding to BMR = 200% (3-fold induction); the plots for other effect sizes are in supplementary Figure S4, available at Mutagenesis Online. As opposed to the in vivo MN data above, the background responses were found to differ significantly among chemicals, but otherwise the model found to adequately describe the combined datasets was the same. Again, the four-parameter exponential model, assumed to have the same shape among chemicals, fits the data appropriately, based on visual inspection of the plots of the individual chemicals (supplementary Figure S3, available at Mutagenesis Online). The entire matrix of BMD data for the in vitro MN studies is shown in Table 2.

Figure 2.

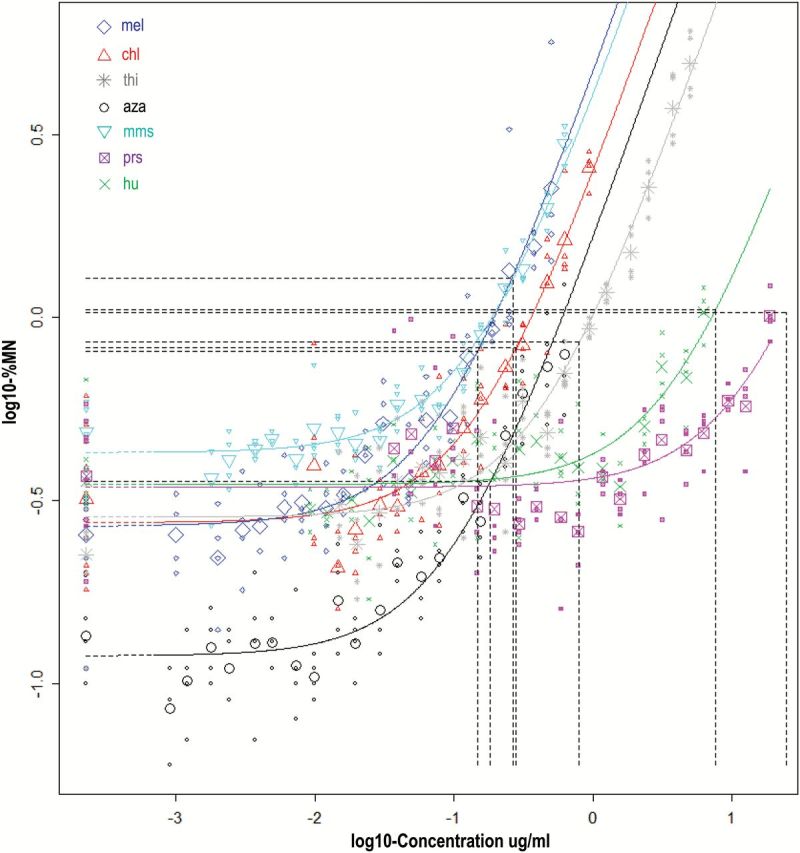
Fitted curves for in vitro MN responses from seven clastogens studied in human TK6 cells. The horizontal-to-vertical dashed lines represent the BMD concentrations that correspond to a BMR = 200%, that is a 3-fold induction of MN (=distance of 0.48 on log10-scale). For each chemical, the small symbols represent the individual data points and the large symbol represents the geometric mean of these observations.

Table 2.

BMD values for in vitro MN assay across varying BMR (units are µg/ml)

	AZA	CHL	HU	MEL	MMS	PRS	THI	Geometric mean
BMR = 0.05
BMD	0.0065	0.0099	0.2706	0.0052	0.0095	0.8737	0.0284
BMDL	0.0047	0.0071	0.2015	0.0038	0.0073	0.6221	0.0199
BMDU	0.0089	0.0140	0.3682	0.0073	0.0127	1.2562	0.0397
BMDU/BMDL	1.88	1.99	1.83	1.94	1.74	2.02	1.99	1.91
BMR = 0.5
BMD	0.0522	0.0798	2.1713	0.0421	0.0764	7.0109	0.2276
BMDL	0.0426	0.0626	1.7343	0.0337	0.0661	5.2717	0.1806
BMDU	0.0635	0.1004	2.7736	0.0520	0.0877	9.7620	0.2821
BMDU/BMDL	1.49	1.60	1.60	1.54	1.33	1.85	1.56	1.56
BMR = 1
BMD	0.0977	0.1493	4.0649	0.0788	0.1431	13.1250	0.4261
BMDL	0.0819	0.1199	3.2729	0.0648	0.1275	9.9183	0.3489
BMDU	0.1163	0.1846	5.1829	0.0953	0.1593	18.2930	0.5134
BMDU/BMDL	1.42	1.54	1.58	1.47	1.25	1.84	1.47	1.50
BMR = 2
BMD	0.1830	0.2796	7.6116	0.1475	0.2679	24.5770	0.7978
BMDL	0.1564	0.2284	6.1307	0.1237	0.2437	18.5530	0.6716
BMDU	0.2142	0.3419	9.7468	0.1758	0.2937	34.4380	0.9389
BMDU/BMDL	1.37	1.50	1.59	1.42	1.20	1.86	1.40	1.46
BMR = 4
BMD	0.3428	0.5238	14.2600	0.2764	0.5018	46.0430	1.4946
BMDL	0.2961	0.4319	11.4010	0.2344	0.4595	34.5140	1.2847
BMDU	0.3984	0.6383	18.4490	0.3271	0.5505	65.1430	1.7303
BMDU/BMDL	1.35	1.48	1.62	1.40	1.20	1.89	1.35	1.45

Cross system correlations

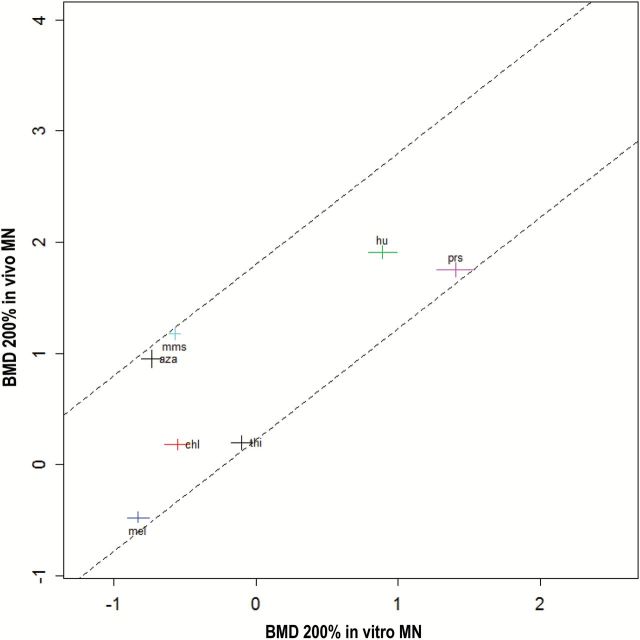
Figure 3 shows the cross system plot comparing in vitro MN BMDs to in vivo MN BMDs, both at BMR = 200% (supplementary Figure S5, available at Mutagenesis Online, for plots with other BMR values). The confidence intervals for each BMD are shown by the horizontal and vertical lines. To quantitatively represent the correlation between the test systems, the diagonal lines in Figure 3 were applied manually to encompass the confidence intervals associated with each of the reported chemicals. These diagonal lines in the double-log plot have unity slope, which translates into a proportional relationship on the original scales. The vertical distance between these two lines may be considered a measure of the correlation between the two systems (see Materials and methods for explanation). Across the different BMR values studied, there was very little difference in this vertical distance: for the BMR values 0.05, 0.5, 1, 2 and 4, the distance was 1.71, 1.61, 1.59, 1.58 and 1.57 units, respectively. The reason for these small differences is that the fitted dose–response curves for the various chemicals are parallel, so that any change in the BMR will not affect the relative positions of the BMDs. In addition, the width of the BMD confidence intervals (=BMDU/BMDL) does not decrease very much when increasing the values of the BMR (see BMDU/BMDL ratios in Tables 1 and 2).

Figure 3.

In vivo MN versus in vitro MN responses for seven clastogens. BMD200 is the BMD corresponding to a BMR = 200%, that is a 3-fold induction of MN. Confidence intervals for each chemical are shown as the horizontal and vertical lines at each data point. The correlation between these two methods is represented by the diagonal lines that encompass the confidence intervals of all chemicals studied.

Discussion

The genotoxicants studied here are well known DNA damaging agents that elicit a specific form of chromosomal damage that can ultimately lead to carcinogenicity. This damage mainly takes the form of strand breakage, some of which will result in DNA double strand breaks and formation of acentric chromatid fragments that can then go on to form MN. Since both the in vitro and in vivo MN assays are sensitive to such chromosomal damage, an examination of the ability of these methods to compare clastogenic compounds in terms of potency is useful for confirming the utility of these assays and supporting their use for direct involvement in human risk assessment.

The in vivo MN data employed for these studies were obtained from work being performed as part of ongoing methodological development studies at Litron that were characterized by extensive dose ranges, adequate number of animals and doses, and typically 20000 reticulocytes scored per sample (7–9). The specific compounds examined here are characterised by varying degrees of clastogenic potency based on the fact that they induce a pre-specified level of chromosomal damage, for example 200% above baseline, at higher or lower concentrations. This can be seen by the distribution of the curves and their associated BMDs along the x-axis in Figure 1 and the data in Table 1, where MEL was the most potent MN-inducer, that is lowest BMD confidence interval, and either HU or PRS (their BMD confidence intervals overlap) the least potent. Figure 4 (lower panel) depicts the confidence intervals of the in vivo MN data for BMR = 200% as a means to visually compare overlap between chemicals and judge potency (supplementary Figure S6, available at Mutagenesis Online). These extensive in vivo studies formed the basis for conducting an analogous set of in vitro MN experiments to determine the responses of the same chemicals in human TK6 cells. Similar to the in vivo data, the dose–response curves for the in vitro MN studies shown in Figure 2 and the confidence interval plot in Figure 4 (upper panel) serve to rank the chemicals from most potent, MEL/AZA, to least, in this case PRS.

Figure 4.

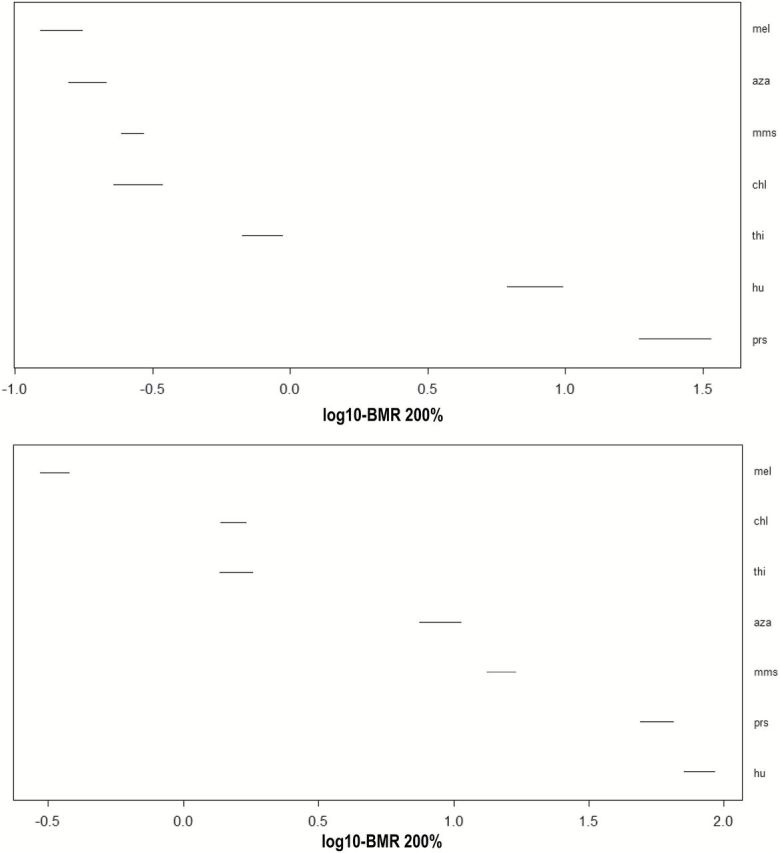
BMD confidence intervals for in vitro (upper panel) or in vivo (lower panel) MN systems corresponding to a BMR = 200%, that is a 3-fold induction of MN.

One observation that can be made from these clastogenicity rankings across the two test systems is the apparent shift in potency of MMS and AZA. Thus for the in vitro studies these compounds appear to be more potent chromosomal damage inducers, that is they have lower BMDs, than for the in vivo system. Likely this is due to the different toxicokinetics that exist between whole animal and cell culture-based systems. Additional experiments to more closely define the mechanism(s) responsible for this are beyond the scope of this publication. Despite the impact that toxicokinetic processes in living animals must have, there was still a clear relationship between these systems as demonstrated in Figure 3.

The methodology for examining the two test systems was based on both the previously mentioned recommendation from the IWGT QWG (2), and on similar investigations reported in the literature. Thus Hernández et al. (19) described a study that matched data from 18 compounds studied in long-term in vivo carcinogenicity studies with information on responses of the same chemicals from in vivo MN, transgenic rodent mutation or in vivo comet studies. Correlations generated from BMDL₁₀ data showed a positive relationship between the potency of the compounds in eliciting elevations in the short-term genetox studies when compared with the potency of the compounds for inducing cancer. This study was later expanded to include data from a total of 48 compounds investigated across both long-term carcinogenicity and in vivo MN study designs (18,20). Again, a clear positive correlation between cancer potency and clastogenic potency was found.

Thus an important outcome of the Hernández et al. studies is that the data support the possibility of using information obtained from a relatively simple short-term assay, for example in vivo MN, to predict carcinogenic potency (18,20). This concept, in combination with other initiatives to reduce or refine the conduct of carcinogenicity testing in product safety programs (21) may ultimately lead to better resource allocation and more effective use of animals to provide quantitative information on cancer risk that can be used for human health-based regulatory decision making, even in the absence of 2-year carcinogenicity study data.

Our investigation showed a similar positive relationship between in vitro and in vivo potency of MN induction (Figure 3), demonstrating that the compounds which were very potent MN inducers in a cell culture model were also very effective at the formation of MN in a whole animal model, and, vice versa, for less potent MN inducers. This finding supports L. G. Soeteman-Hernández, M. D. Fellows, G. E. Johnson, W. Slob (submitted to Tox. Sci.) who also observed a correlation between in vitro and in vivo MN potencies. These observations serve to further strengthen the links that exist between these test systems that are a routine part of genetic toxicology and regulatory review of preclinical safety submission for pharmaceuticals and other consumer or industrial products. Further investigations on the role of metabolism and toxicokinetics might improve the correlation between in vivo and in vitro potencies of MN induction. In addition, more chemicals would need to be included. If the correlation then remains, or even improves by taking toxicokinetics into account, this result may be useful for in vitro to in vivo extrapolation and support the application of alternatives to animal testing for certain safety assessment contexts.

The underlying datasets of the present study were relatively large, with more doses/concentrations than usual. As a result, the BMD confidence intervals were smaller than in the other correlation studies mentioned (18–20). These results are therefore a good starting point for examining the impact of toxicokinetics on the scatter among the chemicals in the correlation plot, as that scatter cannot be explained by imprecise BMD estimates due to limited datasets.

The studies reported here provide support for the earlier finding (6) that dose–response data in general can be adequately described by a four-parameter exponential model. Further, they support the finding in the same study (6) that there is little difference between the dose–response shapes among the chemicals (for the same endpoint in the same test system). As Figures 1 and 2 illustrate, the dose-responses of all seven chemicals are adequately described by dose–response curves having identical shapes. This fact can be used to better estimate the BMDs for each chemical by fitting the model to the seven datasets combined. While the BMDs are allowed to be different in fitting the model, the shape parameters are held constant among chemicals, so that a much larger number of datapoints are available for estimating those shape parameters [c and d, see expression (1) in ref. (6)]. By having more precise estimates for c and d, the BMD confidence intervals will be narrower as well. For an illustration of this phenomenon in a collection of real datasets, see Fig. 11 in reference (6).

Furthermore, this combined approach to dose–response analysis explains why the relative positions of the BMD confidence intervals among chemicals do not change for different values of the BMR, so that the correlation plots are hardly sensitive to the choice of the BMR. The BMD confidence intervals will only increase minimally with decreasing BMR. Apart from this small change in the width of the confidence intervals (=BMDU/DBML), a given BMD confidence interval calculated for a particular BMR can be directly translated into a BMD confidence interval for another BMR [using the estimated parameters c and d in the exponential model; see expression (2) in ref. (6)].

By gaining a better understanding of the relationships between these and other genetic toxicology assays, not only can we expand their contribution to risk assessment, we can more effectively consider alternate study designs that may further maximise the utility of comprehensive datasets that can be readily obtained through the use of efficient, high-throughput methodologies. The continued evolution of genetic toxicology away from simple hazard identification depends on the adoption of quantitative tools found to be effective in other areas of toxicology and developing the knowledge base to implement them effectively.

Funding

This work was supported in part by the National Institute of Environmental Health Sciences (R44ES018017 and R44ES021973).