Feature selection by optimizing a lower bound of conditional mutual information

Abstract

A unified framework is proposed to select features by optimizing computationally feasible approximations of high-dimensional conditional mutual information (CMI) between features and their associated class label under different assumptions. Under this unified framework, state-of-the-art information theory based feature selection algorithms are rederived, and a new algorithm is proposed to select features by optimizing a lower bound of the CMI with a weaker assumption than those adopted by existing methods. The new feature selection method integrates a plug-in component to distinguish redundant features from irrelevant ones for improving the feature selection robustness. Furthermore, a novel metric is proposed to evaluate feature selection methods based on simulated data. The proposed method has been compared with state-of-the-art feature selection methods based on the new evaluation metric and classification performance of classifiers built upon the selected features. The experiment results have demonstrated that the proposed method could achieve promising performance in a variety of feature selection problems.

1. Introduction

Feature selection has been an important component in machine learning, especially in studies with high-dimensional data. Since the high-dimensional data typically contain irrelevant or redundant features, selecting a compact, informative subset of features not only reduces the computational cost for data analysis, but also potentially improves the pattern recognition performance [1,6,24,25]. Feature selection is also able to enhance the interpretability of intrinsic characteristics of the high-dimensional data [5,8,22].

In general, feature selection methods can be categorized into 3 groups: filter methods [4,13,27,31,44], wrapper methods [23,26,35], and embedded methods [7,11,46,49,50]. The filter methods rank features according to their relevancy to the problem under study, gauged by proxy measures that are independent of pattern recognition models to be used in the data analysis. The wrapper methods select features to optimize a pattern recognition model’s performance, and they typically have higher computational cost than the filter methods. The embedded methods typically integrate the feature selection with the pattern recognition model learning, and can achieve good performance with moderate computational cost. Particularly, sparsity regularization based algorithms are representative embedded methods and have attracted much attention in recent years [11,34,37–41,50]. Recent advances in feature selection not only improve pattern recognition performance but also expand applications including multi-label classification, innovation management, and microarray and omics data analysis [1,6,13,19,24,25,29,31,33,52]. In this study, we focus on the filter methods that measure the relevancy of features to a pattern recognition problem under study based on information theoretical criteria.

In the past two decades, many information theoretical criteria have been proposed for feature selection [2,8,47]. Mutual information (MI) based feature selection methods, referred to as Mutual Information Maximization (MIM), have been widely adopted in feature selection studies [8,9,30]. MIM adopts mutual information to measure each feature’s relevancy to the class label, which does not consider redundancy and complementariness among features. An improved method, referred to as Mutual Information Feature Selection (MIFS), is able to reduce the redundancy of the selected features [3], and many variants of MIFS have been developed [28,45,48]. Particularly, Min-Redundancy Max-Relevance (mRMR) selects features with a trade-off between relevancy and redundancy of the selected features [42]. Moreover, several feature selection methods have been proposed to take relevance, redundancy, and joint effects of multiple features together into consideration [14,18,20,32,36,51]. For example, Joint Mutual Information (JMI) has been adopted to measure joint redundant and complementary effect of features in feature selection methods [36,51], and Conditional Mutual Information Maximization (CMIM) utilizes a min-max principle to exploit the joint effects of features in feature selection [14,18]. The feature selection methods based on information theoretical criteria have been successfully applied to many problems. However, most of them are manually-designed heuristics, aiming to simultaneously maximize the relevance of features and minimize redundancy among features [8].

In this study, we first present a theoretical framework for information theory based feature selection using Bayesian error rate and Fano’s Inequality [17,43]. Under this framework, most of the existing information theory based feature selection methods can be interpreted as maximizing a lower-order approximation of conditional mutual information between features to be selected and the class label, given features that have been selected under different assumptions. An improved method is then proposed to select features by Optimizing a Lower Bound of Conditional Mutual Information (OLB-CMI) with a weaker assumption, motivated by the principle of Occam’s Razor that the assumption is weaker, the method would have better generalization performance. The OLB-CMI method also integrates a plug-in component to distinguish redundant features from irrelevant ones, which improves the feature selection robustness when most of the features to be selected are irrelevant. To evaluate the performance of feature selection, a novel metric is proposed to directly measure feature selection precision of feature selection methods based on data with ground truth. This evaluation metric has been adopted to evaluate the proposed feature selection method, 3 information theoretical methods including MIM, JMI and mRMR, 2 classical filter methods including Fisher Score (FS) [4] and ReliefF [27], and 2 sparsity regularization based feature selection methods including Least Absolute Shrinkage and Selection Operator (LASSO) [46] and Discriminative Least Squares Regression for Feature Selection (DLSR-FS) [37,50]. We also evaluated the proposed method based on classification performance of classifiers built on the selected features on 12 publicly available datasets, and compared it with the aforementioned 7 feature selection algorithms.

The remainder of the paper is organized as follows. In Section 2, background knowledge of mutual information is presented; then a unified theoretical framework for information theoretical methods is proposed in Section 3 ; OLB-CMI is presented in Section 4 ; a new metric to gauge the performance of feature selection is proposed in Section 5 ; the experimental results for evaluating feature selection methods is presented in Section 6 ; and finally in Section 7 this paper is concluded with discussions.

2. Background

In this paper, upper case alphabets, such as A, B, and X, denote random variables; lower case alphabets, such as a, b and x, denote samples of random variables denoted by their corresponding upper case alphabets; p (·) denotes a probability distribution function, and p (· | ·) denotes a conditional probability distribution function; H (·) denotes entropy, I (· ; ·) denotes MI between two variables, and I (· ; · | ·) denotes CMI. All the random variables can be multi-dimensional.

Definition 1

For random variables A, B, and C, with domains 𝒜, ℬ and 𝒞, respectively, the conditional mutual information between A and B given C is defined as:

$$I(A;B\mid C)-\sum _{a\in \mathcal{A}}\sum _{b\in \mathcal{B}}\sum _{c\in \mathcal{C}}p(a,b,c)\mathit{log}\frac{p(a,b\mid c)}{p(a\mid b)p(b\mid c)}.$$

When A and B are conditionally independent given C, i.e., p(a, b| c) = p(a | c) p(b| c), or p(b| a, c) = p(b| c), I(A ; B | C) = 0.

Lemma 1

If random variable A is independent of joint random variables (B, C), the conditional mutual information I (A ; B | C) is equal to zero:

$$I(A;B\mid C)=0$$

Proof

Since p(a, b, c) = p(a) p(b, c), Σ_b∈ℬ p(a, b, c) = Σ_b∈ℬ p(a) p(b, c). Therefore, p(a, c) = p(a) p(c). Then, we have p(a | c) = p(a) and $p(a,b\mid c)=\frac{p(a,b,c)}{p(c)}=\frac{p(a)p(b,c)}{p(c)}=p(a)p(b\mid c)=p(a\mid c)p(b\mid c)$.

Lemma 2

If random variable A is a deterministic function of random variable C, the conditional mutual information I (A ; B | C) is equal to zero:

$$I(A;B\mid C)=0.$$

Proof

Since A = f (C), p(b| a, c) = p(b| c). Therefore, we have I(A ; B | C) = 0.

Note that these conclusions are valid when A, B, C are multi-dimensional random variables.

3. An unified framework for information theoretic criteria based feature selection

Given a pattern classification problem with a training dataset {(xⁱ, cⁱ), i = 1, …, N}, where xⁱ is a D-dimensional training data point and cⁱ is its associated class label. xⁱ and cⁱ are considered as independent identically distributed (i.i.d.) samples of their corresponding random variables X = {X_j, j = 1, … D} and C, respectively. Each element X_j of X is referred t o as a feature.

Bayesian error rate of a given classification problem has a lower bound measured by the mutual information between features and the class label, as defined by Fano’s inequality [17,43] :

$$P(\widehat{C}\ne C)=P(E)\ge \frac{H(C)-I(\stackrel{\sim }{\mathit{X}};C)-1}{\mathit{log}(ℂ)},$$ (1)

where Ĉ is the predicted classification label obtained based on given features $\stackrel{\sim }{\mathit{X}},E=\{\begin{array}{lll}1\hfill & if\hfill & \widehat{C}\ne C\hfill \\ 0\hfill & if\hfill & \widehat{C}=C\hfill \end{array}$ is a random variable of Bayesian error, P (E) is the Bayesian error rate, and ℂ is the number of classes.

Fano’s inequality theoretically indicates that if the mutual information between the selected features and class label is larger, the low bound of Bayesian error rate will be smaller. Thus, the feature selection can be directly modeled as an optimization problem to find X_*, a subset of X, so that it’s mutual information with the class label C is maximized.

$${\mathit{X}}_{\mathbf{\ast }}=\underset{{\mathit{X}}_{\mathit{S}}\in \mathit{X}}{\text{argmax}}(I({\mathit{X}}_{\mathit{S}};C)),$$ (2)

where X_S = X_S^d = {X_s(1), X_s(2), …, X_s(d)} is a subset with d features. We denote the set of unselected features by X_S̄ = {X_s̄(1), X_s̄(2), …, X_s̄(D–d)}, denote X_S without X_i by X_S/i (X_i ∈ X_S), and denote an unselected feature by X_k^d or X_k.

Since it is a NP-hard problem to search all possible subsets [44], a suboptimal greedy forward searching strategy is typically adopted to select features. Given an optimal subset of features, X_S^d, that has been selected, then the (d + 1)^th feature, X_*, to be selected should be able to maximize

$$X_{\ast }=\underset{X_k\in {\mathit{X}}_{\overline{\mathit{S}}}}{\text{argmax}}(I({\mathit{X}}_{{\mathit{S}}^d},X_k;C)).$$ (3)

Since I(X_S^d;C) is known, the optimization problem of Eq. (3) is equivalent to maximizing the incremental mutual information:

$$X_{\ast }=\underset{X_k\in {\mathit{X}}_{\overline{\mathit{S}}}}{\text{argmax}}(I({\mathit{X}}_{{\mathit{S}}^d},X_k;C)-I({\mathit{X}}_{{\mathit{S}}^d};C)).$$ (4)

Maximizing the incremental mutual information can be formulated as the maximization of CMI

$$X_{\ast }=\underset{X_k\in {\mathit{X}}_{\overline{\mathit{S}}}}{\text{argmax}}(I(X_k;C\mid {\mathit{X}}_{{\mathit{S}}^d})).$$ (5)

For the forward searching based feature selection, we present another relationship between Bayesian error rate and CMI (or increment mutual information) between the features and class label for forward feature selection formulated in Eq. (4), as stated in Theorem 1.

Theorem 1

With more features being selected, incremental Bayesian error rate is less or equal to zero. If and only if conditional mutual information between the features to be selected and the class label given the selected features is equal to zero, the equality holds.

Proof

Given an arbitrary feature X₁, Bayesian error rate with X₁ can be derived as:

$$P(E_1)=\int P(e_1,{\mathit{x}}_1)d{\mathit{x}}_1=\int P(e_1\mid {\mathit{x}}_1)p({\mathit{x}}_1)d{\mathit{x}}_1,$$ (6)

where P (e₁ | x₁) = min [1 − P (c₁ | x₁), 1 − P (c₂ | x₁), P (c₃ | x₁) …] and [c₁, c₂, c₃, …] is the sample space of the class label C.

Then, adding a feature X₂, Eq. (6) can be reformulated as

$$P(E_1)=\iint P(e_1,{\mathit{x}}_1,{\mathit{x}}_2)d{\mathit{x}}_{1}d{\mathit{x}}_2=\iint P(e_1\mid {\mathit{x}}_1,{\mathit{x}}_2)p({\mathit{x}}_1,{\mathit{x}}_2)d{\mathit{x}}_{1}d{\mathit{x}}_2.$$ (7)

Similarly, Bayesian error rate with X₁ and X₂ is

$$P(E_2)=\iint P(e_2,{\mathit{x}}_1,{\mathit{x}}_2)d{\mathit{x}}_{1}d{\mathit{x}}_2=\iint P(e_2\mid {\mathit{x}}_1,{\mathit{x}}_2)p({\mathit{x}}_1,{\mathit{x}}_2)d{\mathit{x}}_{1}d{\mathit{x}}_2,$$ (8)

where P (e₂ | x₁, x₂) = min [1 − P (c₁ | x₁, x₂), 1 − P (c₂ | x₁, x₂), 1 − P (c₃ | x₁, x₂) …] and [c₁, c₂, c₃, …] is the sample space of the class label C.

Combining Eq. (7) and Eq. (8), we have

$$P(e_2\mid {\mathit{x}}_1,{\mathit{x}}_2)\le P(e_1\mid {\mathit{x}}_1,{\mathit{x}}_2).$$ (9)

Thus, the incremental Bayesian error rate is less than or equal to zero, i.e., P (E₂) – P (E₁) ≤ 0. If and only if p(c | x₁, x₂) = p(c| x₁), the equality holds. Actually, when p(c | x₁, x₂) = p(c| x₁), incremental mutual information or conditional mutual information between X₂ and C given X₁ is also equal to zero: I(X₁, X₂ ;C) – I(X₁, ;C) = I(X₂ ;C| X₁) = 0. Then, we can obtain the conclusion.

Remark 1

Theorem 1 theoretically justifies the intuitive fact that irrelevant features and redundant features are non-informative or useless to lower Bayesian error rate. If a feature to be selected, X_k, is an irrelevant feature, i.e., X_k is jointly independent of the selected features and the class label (X_S^d, C), according to Lemma 1 the conditional mutual information I(X_k ;C| X_S^d) = 0, indicating that the increment Bayesian error is equal to zero. If X_k is redundant, i.e., X_k = f (X_S^d), according to Lemma 2 the conditional mutual information I(X_k ;C | X_S^d) = 0, indicating that the increment Bayesian error is also equal to zero.

Although the forward strategy can address the NP-hard problem, the computational cost of high-dimensional CMI is prohibitive with the increasingly selected features because of curse of dimensionality. In practice, most of the existing information theoretical feature selection methods approximate the CMI with no more than 3 variables, and use heuristics to simultaneously maximize the relevance of features and minimize redundancy among the selected features [8]. In following, we will illustrate that most of the heuristic strategies are essentially low-dimensional approximations of the high-dimensional CMI modeled by Eq. (2) or Eq. (5) with different assumptions. Particularly, we choose 3 representative methods, including MIM, JMI, and mRMR. The MIM method is the basic form of the information theory based feature selection methods, while JMI and mRMR have better performance for feature selection among existing information based methods [8]. According to the principle of Occam’s Razor, the weaker assumptions adopted in a method, the better generalization performance the method will have. Therefore, this framework can enable us to theoretically evaluate and compare these algorithms.

3.1. Mutual Information Maximization (MIM)

MIM selects features based on the mutual information between each feature and the class label without taking joint effects of features into consideration [9,30], i.e.,

$$X_{\ast }=\underset{X_k\in \mathit{X}}{\text{argmax}}(I(X_k;C)),$$ (10)

which can be derived from Eq. (2) based on Assumption 1 and Assumption 2.

Assumption 1

All features are mutually independent, i.e.,

$$p({\mathit{x}}_{\mathit{s}})=\prod _{x_k\in {\mathit{x}}_{\mathit{s}}}p(x_k).$$ (11)

Assumption 2

All features are mutually conditionally independent given the class label, i.e.,

$$p({\mathit{x}}_{\mathit{s}}\mid c)=\prod _{x_k\in {\mathit{x}}_{\mathit{s}}}p(x_k\mid c).$$ (12)

Proposition 1

The optimization problem of MIM and Eq. (2) have the same solution if Assumption 1 and Assumption 2 are satisfied.

Proof. is presented in Appendix. A.

MIM is a simple and intuitive information theory based feature selection method. However, Assumption 1 and 2 are so strong that they cannot be satisfied in most real applications. Therefore, the performance of MIM is often limited.

3.2. Joint Mutual Information (JMI)

JMI was first proposed by Yang and John [51], and was further developed by Meyer et al. [36]. JMI can be modeled as [51] :

$$X_{\ast }=\underset{X_k\in {\mathit{X}}_{\overline{\mathit{S}}}}{\text{argmax}}\left(\sum _{X_i\in {\mathit{X}}_{\mathit{S}}}I(X_i,X_k;C)\right).$$ (13)

This method can be derived from Eq. (5) if Assumptions 3 and 4 are satisfied.

Assumption 3

Any one of the unselected features is conditionally independent of union of the selected features after removing a feature given the removed feature itself, i.e.,

$$p(x_k;{\mathit{x}}_{\mathit{s}/i}\mid x_i)=p(x_k\mid x_i)p({\mathit{x}}_{\mathit{s}/i}\mid x_i).$$ (14)

Assumption 4

Any one of the unselected features is conditionally independent of union of the selected features after removing any feature given the class label and the removed feature itself, i.e.,

$$p(x_k;{\mathit{x}}_{\mathit{s}/i}\mid ,x_i,c)=p(x_k\mid x_i,c)p({\mathit{x}}_{\mathit{s}/i}\mid x_i,c).$$ (15)

Proposition 2

The optimization problem of JMI and Eq. (5) have the same solution if Assumption 3 and Assumption 4 are satisfied.

Proof. is provided in Appendix. B.

Assumption 3 is weaker than Assumption 1. If Assumption 1 is satisfied, X_k is independent of joint random variable (X_S/i, X_i), and the proof of Lemma 1 indicates that p(x_k; x_s/i|x_i) = p(x_k|x_i) p(x_s/i|x_i). Thus, Assumption 3 is satisfied, but not vice versa. Assumption 4 is also weaker than Assumption 2. If Assumption 2 is satisfied, X_k is conditionally independent of X_S and X_i given C, indicating that p(x_k|x_s/i, x_i, c) = p(x_k|c) = p(x_k|x_i, c). Thus, Assumption 4 is satisfied, but not vice versa. Therefore, JMI would have better feature selection performance than MIM.

3.3. Minimum Redundancy and Maximum Relevance (mRMR)

mRMR criterion is a combination of relevance and redundancy terms [15,42]. The feature selection based on mRMR is to find features that have the best trade-off between relevance and redundancy of the selected features, i.e.,

$$X_{\ast }=\underset{X_k\in {\mathit{X}}_{\overline{\mathit{S}}}}{\text{argmax}}\left(I(X_k;C)-\frac{1}{d}\sum _{X_i\in {\mathit{X}}_{\mathit{S}}}I(X_i;X_k)\right),$$ (16)

where d is the cardinality of X_S, I(X_k; C) is the relevance term, and $\frac{1}{d}{\sum }_{X_i\in {\mathit{X}}_{\mathit{S}}}I(X_i;X_k)$ is the redundancy term. mRMR can be derived from Eq. (5) if Assumption 3 and Assumption 5 are satisfied.

Assumption 5

Any one of the unselected features is conditionally independent of union of the selected features given the class label, i.e.,

$$p(x_k;{\mathit{x}}_{\mathit{s}}\mid c)=p(x_k\mid c)p({\mathit{x}}_{\mathit{s}}\mid c).$$ (17)

Proposition 3

The optimization problem of mRMR and Eq. (5) have the same solution if Assumption 3 and Assumption 5 are satisfied.

Proof. is provided in Appendix. C.

Assumption 5 is weaker than Assumption 2. If Assumption 2 is satisfied, X_k is conditionally independent of X_S given C. Thus, Assumption 5 is satisfied, but not vice versa. Therefore, mRMR would have better feature selection performance than MIM.

4. Feature selection by optimizing a lower bound of CMI

Most of the existing information theory based feature selection algorithms adopt feature selection criteria that are low-order approximation of the high-dimensional CMI modeled by Eq. (5) with different assumptions. Motivated by the principle of Occam’s Razor, we propose a novel feature selection algorithm, referred to as optimizing a lower bound of CMI (OLB-CMI), by adopting a relatively weaker assumption. Instead of directly optimizing CMI, we propose to optimize its lower bound, i.e.,

$$X_{\ast }=\underset{X_k\in {\overline{\mathit{X}}}_{\mathit{S}}}{\text{argmax}}\left(\underset{X_i\in {\mathit{X}}_{\mathit{S}}}{\text{max}}I(X_i,C;X_k)-I(X_{i\ast };X_k)\right),$$ (18)

where $X_{i\ast }=\underset{X_i\in X_S}{\mathit{argmax}}(I(X_i,C;X_k))$.

Proposition 4

The optimal value of OLB-CMI is a tight lower bound of the optimal value of Eq. (5) if Assumption 3 is satisfied.

Proof. is provided in Appendix.D.

According to Fano’s Inequality, maximizing original high-dimensional CMI in Eq. (5) is not related to the exact Bayesian error rate, but is associated with the low bound of Bayesian error rate. In fact, suggested by Proposition 4, OLB-CMI also tends to lower Bayesian error rate. Furthermore, OLB-CMI reserves the property of the exact high-dimensional CMI model in Eq. (5), i.e., the objective function value of the optimization model in Eq. (18) will be zero if the feature to be selected, X_k, is conditionally independent of the class label C given the selected feature X_i (p(x_k, c|x_i) = p(x_k|x_i) p(c|x_i)). Therefore, OLB-CMI will not select such features that are fully irrelevant or redundant as suggested by Remark 1. However, this property is not preserved in MIM, JMI and mRMR, and they may select fully irrelevant or redundant features.

The optimization problem of Eq. (18) can be solved by following two steps:

• S1For any X_k, find $X_{ki\ast }=\underset{X_i\in {\mathit{X}}_{\mathit{S}}}{\text{argmax}}(I(X_i,C;X_k))$
• S2 $X_{\ast }=\underset{X_k\in {\overline{\mathit{X}}}_{\mathit{S}}\mathit{and}\frac{I(X_{ki\ast },C;X_k)}{H(X_k)}>\alpha }{\text{argmax}}(I(X_{ki\ast },C;X_k)-I(X_{ki\ast };X_k))$,

where α is a parameter.

In particular, S2 has an optional condition, $\frac{I(X_{ki\ast },C;X_k)}{H(X_k)}>\alpha$, which could be used as a plug-in component for rejecting irrelevant features. In the present study, a feature X_k is deemed as an irrelevant one if $\frac{I(X_{ki\ast },C;X_k)}{H(X_k)}\le \alpha$, where H (X_k) is a normalization term and α (0 ≤α ≤1) is a parameter that can be determined using cross-validation. When α = 0, the plug-in component does not play its role in the feature selection. The reason why we set threshold parameter α is following.

Supposing most informative features have been selected, the remaining features are irrelevant or redundant to the problem under study. It is worth noting that fully irrelevant and redundant features are useless (i.e., adding 0 to the approximation of CMI). If features with small values for the approximation of CMI in Eq. (5) are selected, they provide useful information for the classification. Under this circumstance, one may prefer to select the redundant features rather than select those irrelevant ones if the forward feature selection keeps running because irrelevant features may deteriorate the performance of classification models in practice, especially when the number of data samples is small. However, such an issue has not been taken into consideration in the existing information theory based feature selection methods, and they are not equipped to distinguish irrelevant features from redundant features.

For a given feature X_k, if it is an irrelevant feature that is most likely independent of any of the selected features, X_i, and the class label C, max (I (X_i, C; X_k)) will be small. However, if it is a redundant feature that is somewhat dependent on the selected features, max (I (X_i, C; X_k)) will be relatively large. Thus, the proposed OLB-CMI adopts a parameter α for $\frac{I(X_{ki\ast },C;X_k)}{H(X_k)}$ to distinguish redundant features from irrelevant features.

The implementation of OLB-CMI is summarized in Algorithm 1. To simplify the implementation, we estimate probability distributions of random variables using histogram estimators with bins of fixed width. If the number of bins is B and the number of data points is N, the computational cost of mutual information with three variables are O (N + B³). If the number of total features is D and the number of features to be selected is d, according to Algorithm 1, the time complexity of OLB-CMI is O(dD(N + B³)) and the space complexity of OLB-CMI is O (dD). Therefore, OLB-CMI has a similar computational complexity as JMI and mRMR.

Algorithm 1.

implementation of OLB-CMI.

Input : Full feature set X = {X1, X2, X3, …, XD}, class label C, the number of features to be selected d and threshold α

index set of the selected features: S = {}

index set of the unselected features: S̄ = {1, 2, 3, …, D}

for i = 1 to D do

fea_lab_mi[i] = I(Xi, C)

fea_entropy[i] = H(Xi)

end for

$k^{\ast }=\underset{1\le i\le D}{\text{argmax}}(\text{fea}\_\text{lab}\_\text{mi}[i])$

S[1] = k*

S̄ = S̄/k*

for i = 2 to d do

for k = 1: D − i + 1 do

fea_lab_mi [i −1] [ S̄ [k)] = I(XS[i − 1], C; XS̄[k])

$\mathrm{t}=\underset{1\le m\le i-1}{\text{argmax}}(\text{fea}\_\text{lab}\_\text{mi}[\mathrm{m}][\overline{\mathit{S}}[k]])$

if $\left(\frac{I(X_{\mathit{S}[\mathrm{t}]},C;X_{\overline{\mathit{S}}[k]})}{\text{fea}\_\text{entropy}[\overline{\mathit{S}}[k]]}\ge \alpha \right)$ then

max_fea_lab_cmi[S̄[k]] = I(XS[t], C; XS̄[k]) − I(XS[t]; XS̄[k])

else

max_fea_lab_cmi [S̄[k]] = 0

end if

end for

$k^{\ast }=\underset{1\le k\le D-1}{\text{argmax}}(\text{max}\_\text{fea}\_\text{lab}\_\text{cmi}[\overline{\mathit{S}}[k]])$

S[i] = S̄[k*]

S̄ = S̄/S̄[k*]

end for

output: index set of the selected features S

5. Feature selection precision

A new metric is proposed to directly gauge the precision of feature selection methods based on known information of valid (relevant) and irrelevant/redundant features given a dataset, similar to the area under the receiver operating characteristic curve (ROC) for evaluating the classification performance [16]. For a given feature selection result, we can compute two ratios, one for the number of selected features to the total number of features (SF2TF) and the other for the number of selected valid features to the total number of valid features (SVF2TVF).

As illustrated by Fig. 1, based on the aforementioned two ratios, a curve similar to the ROC curve can be obtained, and the area under the curve ranging from 0.5 to 1, referred to as Feature Selection Precision (FSP), can be used to evaluate the feature selection precision. For a random feature selection algorithm, a curve indicated by B in Fig. 1 will be obtained with FSP = 0.5, while an algorithm better than chance will yield a curve similar to A. A higher FSP indicates a more precise feature selection, since the valid features dominates the selected features, while a lower FSP indicates a worse feature selection performance since more irrelevant features are selected. Rather than resorting to proxy measures, such as classification accuracy, this metric can directly evaluate the performance of feature selection models.

Fig. 1.

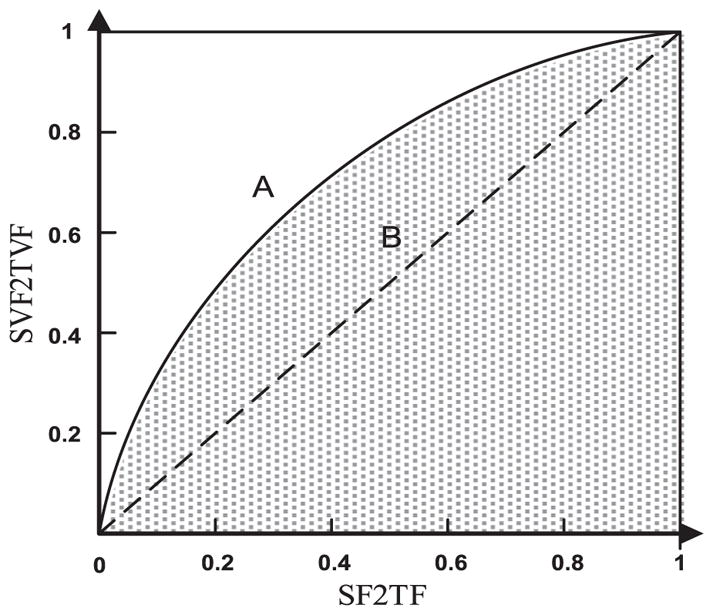
Illustration of Feature Selection Precision (FSP). x axis is selected-features-to-total-features ratio (SF2 TF) and y axis is selected-valid-features-tototal- valid-features ratio (SVF2TVF). The area under the curve is FSP.

6. Experiments

We carried out experiments based on both synthetic data and real-world data to evaluate the performance OLB-CMI and compared it with state-of-the-art information theory based feature selection algorithms, including MIM, JMI and mRMR. We also compared our method with 2 classical filter methods including Fisher Score (FS) [4] and ReliefF [27], and 2 sparsity regularization based feature selection methods including Least Absolute Shrinkage and Selection Operator (LASSO) [46] and Discriminative Least Squares Regression for Feature Selection (DLSR-FS) [37,50].

Based on a simulated dataset, we examined the impact of parameter α in the plug-in component on the performance of OLB-CMI, measured FSP values of different methods. Based on real-world datasets, we compared the classification performance of OLB-CMI with the state-of-the-art feature selection methods.

6.1. Experiments based on a simulated dataset

A synthetic dataset was generated by a similar procedure as used in [21]. Firstly, 30 binary data points with 10-bit were randomly generated a_i = [α_i,1, α_i,2, …, α_i,j, …α_i,10] (1 ≤ i ≤ 30, α_i,j = {−1, 1}) and randomly divided into 2 classes. Based on the 30 data points, n_i = 100 i.i.d. examples for each a_i were generated based on a Gaussian distribution 𝒩 (a_i, I), yielding a data set with n = 3000 examples and d_u = 10 features. Secondly, d_r = 10 redundant features were added to the dataset. They were obtained by point-wise multiplying the useful features by a random n × d_u matrix B with uniformly distributed random numbers between [0.9, 1.1]. Thirdly, elements of d_n = 180 irrelevant features were generated with a Gaussian distribution 𝒩 (0, 1). Fourthly, all the elements of features were corrupted by adding Gaussian noise 𝒩 (0, 0. 2). Finally, 2% of class labels of the data points were randomly exchanged.

Based on the synthetic dataset, we compared classification accuracy of classifiers built on features selected by OLB-CMI with and without the plug-in component. Gaussian-kernel support vector machines (SVMs) were adopted to build classifiers [12]. The dataset was randomly split into training and testing subsets with ratio 6:4, and total 50 random trials were implemented. And an optimal α and hype-parameters of the SVM classifiers were optimized by 10-fold cross validation. The classification results are shown in Fig. 2 and Table 1.

Fig. 2.

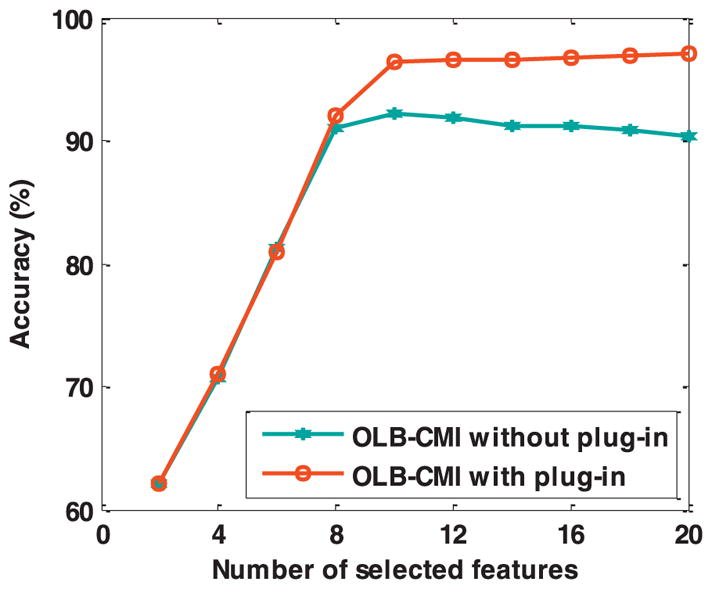
Classification accuracy of SVM classifiers built on features selected by OLB-CMI with and without the plug-in component. The plug-in component’s α was optimized by 10-fold cross validation based on the training samples.

Table 1.

Classification accuracy (%) of SVM classifiers built on the top 20 features selected by OLB-CMI with and without the plug-in component.

Number of Feature	2	4	6	8	10	12	14	16	18	20
OLB-CMI without the plug-in	62.16	70.75	81.19	90.94	92.19	91.82	91.26	91.17	90.84	90.35
OLB-CMI with the plug-in	62.13	70.99	81.00	91.99	96.38	96.60	96.63	96.74	96.89	97.02

As shown in Fig. 1 and Table 1, the features selected by OLB-CMI with and without the plug-in component had similar classification accuracy for the top 8 selected features. However, with more features were selected by OLB-CMI without the plug-in component, their associated classification accuracy decreased consistently, while the features selected by OLB-CMI with the plug-in component could further improve the classification accuracy. These results indicated that an appropriate α in OLB-CMI with the plug-in component could improve the feature selection performance. This is simply because redundant features contain useful information, complementary to the selected features. In contrast, if all the less-informative features are selected without preference, irrelevant features might be selected, resulting in deteriorated classification performance. Therefore, selecting redundant features rather than irrelevant features can help improve the feature selection performance.

Based on the synthetic dataset, we utilized the FSP value to evaluate feature selection performance of different methods under comparison. Specifically, the relevant features were 10 useful features or their duplicates. A relevant feature and its corresponding duplicate were mutual exclusive. If one of them had been selected, the other would not be treated as a relevant feature any more. As shown in Fig. 3 and Table 2, the experimental results indicated that OLB-CMI could select relevant features more precisely, and FSP of OLB-CMI was close to the theoretically optimal value (0.9750), i.e., the top ten features selected by OLB-CMI are all valid features in all 50 trials. The results also demonstrated that JMI, ReliefF, LASSO, and DLSR-FS had better FSP values than others.

Fig. 3.

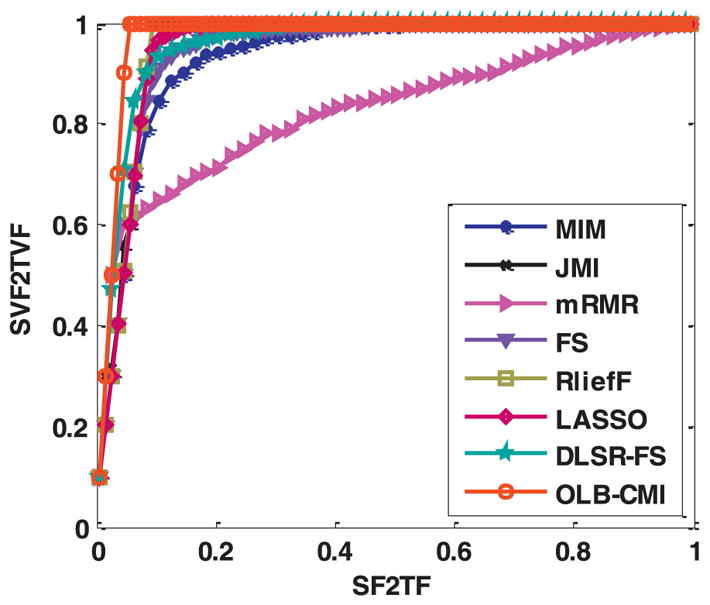
FSP Curves for different feature selection algorithms.

Table 2.

Average FSP for feature selection algorithms.

	MIM	JMI	mRMR	FS	ReliefF	LASSO	DLSR-FS	OLB-CMI
FSP	0.9327	0.9562	0.8279	0.9429	0.9546	0.9518	0.9576	0.9747

6.2. Experiments based on real-world datasets

The feature selection algorithms were also evaluated based on 12 real-world data sets with respect to classification accuracy of classifiers built upon selected features. The 12 datasets are detailed in Table 3.

Table 3.

Dataset information.

Data Sets	#Classes	#Features	#Examples
SEMEION	10	256	1593
ISOLET	26	617	7797
ARCENE	2	10,000	200
GISETTE	2	5000	7000
LUNG	5	3312	203
TOX-171	4	5748	171
WebKB-WT	7	4165	1166
WebKB-WC	7	4189	1210
UMIST	20	2576	575
AR	120	2000	1680
ORL	10	10,304	400
CMU-PIE	64	4096	1636

SEMEION and ISOLET

They were obtained from UCI. ¹ SEMEION contains 1593 handwritten digits images from ~80 persons, stretched in a rectangular box of 16 × 16 with a gray scale of 256. ISOLET is a speech recognition data set with 7797 samples in 26 classes, and each sample has 617 features.

ARCENE and GISETTE

They were obtained from NIPS feature selection challenge.² Both of them are two-class classification datasets with 10,000 and 5000 features, respectively. ARCENE contains data from cancer patients and normal controls, and GISETTE contains 2 handwritten digits: 4 and 9.

WebKB-WT and WebKB-WC³

These datasets comprise about 1200 web pages grouped into 7 classes from computer science departments of two universities: Washington and Wisconsin.

LUNG and TOX-171

These datasets comprise bioinformatics measures. LUNG has 3312 genes with standard deviations larger than 50 expression units [10]. TOX-171 was obtained from feature selection @ ASU,⁴ comprising 171 samples with 5748 features.

UMIST⁵

It includes 575 face images of 56 × 46 from 20 different people, yielding a feature dimension of 2576.

AR⁶

It includes face images of 50 × 40 from 120 different individuals, yielding a feature dimension of 2000. For each individual, 14 images were acquired with different facial expression and illuminations.

ORL⁷

It includes 400 face images of 92 × 112 from 40 different individuals, yielding a feature dimension of 10,304. For each individual, the images were taken by varying lighting, facial expressions and facial details (glasses/no glasses).

CMU_PIE⁸

We selected the frontal pose dataset (09). It contains 64 persons and each person has 24 face images of 64 × 64 taken with different illuminations. The number of features is 4096.

To build classifiers based on selected features, linear-SVM was adopted in the present study [12]. A cross-validation strategy was used to optimize the regularization parameter C for the linear-SVM classification by searching a parameter set [10⁻³, 10⁻², 10 ⁻¹, 1, 10¹, 10², 10³] based on a training dataset for all the feature selection algorithms. For DLSR-FS, we also selected an appropriate λ from the candidate set [10⁻³, 10⁻², 10⁻¹, 1, 10¹, 10², 10³] using cross-validation, resulting in a parameter space { C, λ} with 49 elements. For OLB-CMI, α was also tuned by cross-validation and the candidate set was [0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3], resulting in a parameter space { C, α} with 49 elements.

In the experiments, each dataset was randomly spilt into training and testing subsets. The ratio between the numbers of training and testing samples was 6:4. And a total of 10 trials were run for generating different sets of training and testing samples and the final classification accuracy was the average value of 10 trials. A 3-fold cross-validation was used for datasets with less than 200 training samples, and an 8-fold cross-validation was used for datasets with more than 200 samples.

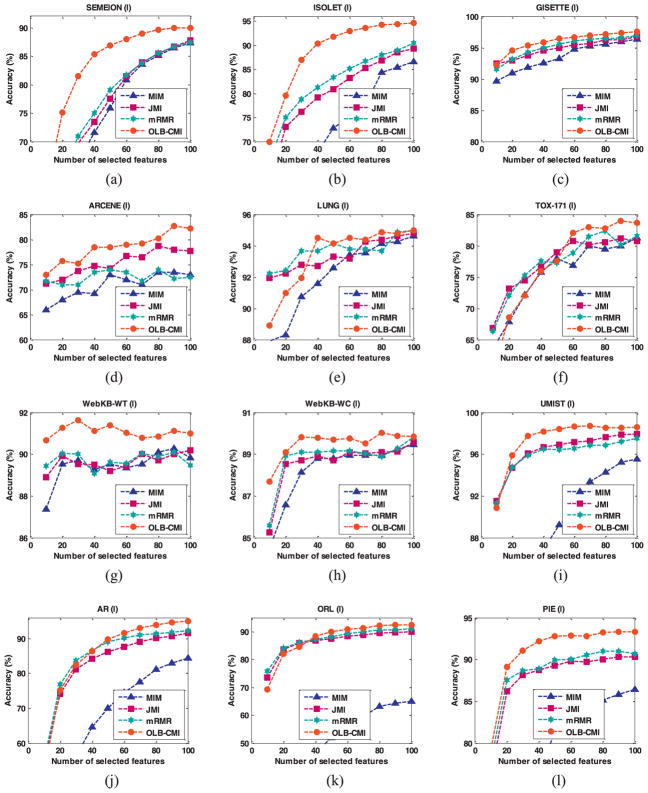
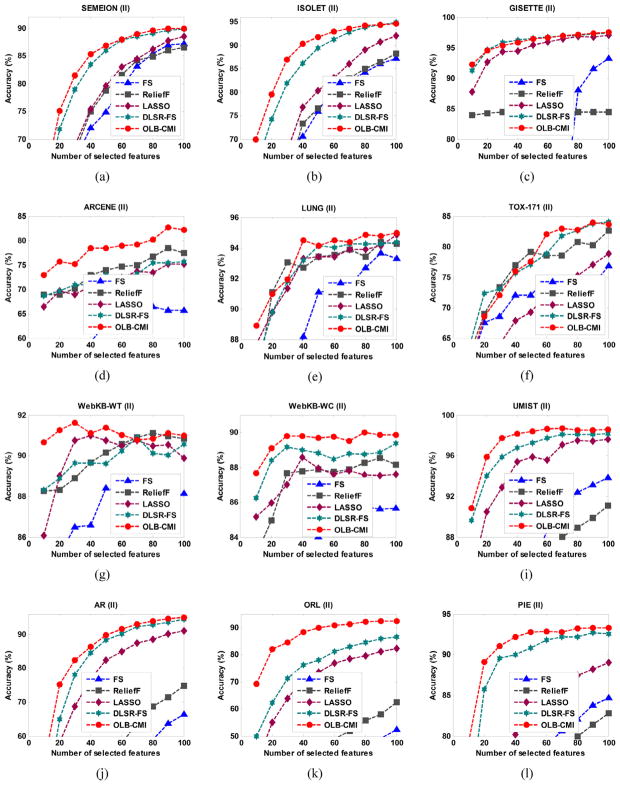
The classification results are shown in 2 different figures by clustering the 8 feature selection methods into 2 groups. Fig. 4 shows comparison results among our method, MIM, JMI, and mRMR, and Fig. 5 shows comparison results among our method, FS, ReliefF, LASSO and DLSR-FS. The average classification accuracy and the standard deviation on the top selected 40 and 80 features for each dataset are summarized in Table 4, Table 5, Table 6 and Table 7, respectively.

Fig. 4.

Average classification accuracy of 10 trials of classifiers built on features selected by different information theory based feature selection methods: MIM, JMI, mRMR, and OLB-CMI. The results shown were on (a) SEMEION, (b) ISOLET, (c) ARCENE, (d) GISETTE, (e) LUNG, (f) TOX-171, (g) WebKB-WT, (h) WebKB-WC, (i) UMIST, (j) AR, (k) ORL, (l) CMU-PIE.

Fig. 5.

Average classification accuracy of 10 trials of classifiers built on features selected by different feature selection methods: FS, ReliefF, LASSO, DLSR-FS and OLB-CMI. The results shown were on (a) SEMEION, (b) ISOLET, (c) ARCENE, (d) GISETTE, (e) LUNG, (f) TOX-171, (g) WebKB-WT, (h) WebKB-WC, (i) UMIST, (j) AR, (k) ORL, (l) CMU-PIE.

Table 4.

Mean and standard deviation of the classification rates (%) of classifiers built on the top 40 features selected by OLBCMI, MIM, JMI and mRMR.

	MIM	JMI	mRMR	OLB-CMI
SEMEION	71.60 ± 1.35	73.50 ± 1.42	75.02 ± 1.11	85.39 ± 1.42
ISOLET	67.99 ± 1.42	79.20 ± 0.66	81.28 ± 1.04	90.31 ± 1.21
ARCENE	69.13 ± 5.47	74.75 ± 4.96	73.38 ± 4.25	78.50 ± 3.25
GISETTE	92.60 ± 0.37	94.58 ± 0.35	95.22 ± 2.18	95.85 ± 3.47
LUNG	91.59 ± 1.39	92.68 ± 1.09	93.66 ± 1.95	94.51 ± 1.57
TOX-171	75.80 ± 6.31	76.67 ± 5.84	77.54 ± 5.91	75.94 ± 5.11
WebKB-WT	89.27 ± 1.48	89.49 ± 1.57	89.08 ± 1.22	91.11 ± 1.17
WebKB-WC	88.78 ± 0.71	88.90 ± 0.85	89.11 ± 0.82	89.79 ± 0.90
UMIST	86.78 ± 4.16	96.65 ± 1.56	96.48 ± 1.39	98.17 ± 0.93
AR	64.60 ± 3.22	84.20 ± 2.27	86.50 ± 2.15	86.44 ± 1.84
ORL	46.75 ± 11.77	86.75 ± 2.51	87.13 ± 2.93	88.44 ± 2.81
CMU-PIE	76.35 ± 2.92	88.71 ± 1.68	88.87 ± 1.32	92.18 ± 0.91

Table 5.

Mean and standard deviation of the classification rates (%) of classifiers built on the top 80 features selected by OLBCMI, MIM, JMI and mRMR.

	MIM	JMI	mRMR	OLB-CMI
SEMEION	85.08 ± 1.04	85.50 ± 1.14	85.60 ± 1.01	89.59 ± 1.07
ISOLET	84.36 ± 0.78	86.88 ± 0.53	88.02 ± 0.70	94.23 ± 0.37
ARCENE	73.38 ± 4.97	78.63 ± 3.08	73.88 ± 4.95	80.25 ± 4.28
GISETTE	95.52 ± 0.64	96.20 ± 0.52	96.50 ± 0.35	97.14 ± 0.45
LUNG	94.15 ± 1.62	94.39 ± 1.24	93.66 ± 1.79	94.88 ± 2.03
TOX-171	79.42 ± 5.01	80.58 ± 6.80	82.32 ± 4.92	82.75 ± 4.82
WebKB-WT	90.11 ± 0.93	89.72 ± 1.22	89.89 ± 1.23	90.86 ± 0.78
WebKB-WC	88.95 ± 1.28	89.09 ± 1.28	88.88 ± 1.34	90.02 ± 0.83
UMIST	94.30 ± 1.56	97.61 ± 0.90	96.87 ± 1.53	98.52 ± 1.09
AR	81.06 ± 1.80	90.19 ± 1.69	91.37 ± 1.83	93.97 ± 1.82
ORL	63.25 ± 10.08	89.50 ± 2.34	90.69 ± 2.08	92.19 ± 2.74
CMU-PIE	85.11 ± 1.86	90.00 ± 1.20	90.95 ± 1.02	93.25 ± 0.62

Table 6.

Mean and standard deviation of the classification rates (%) of classifiers built on the top 40 features selected by OLB-CMI, FS, ReliefF, LASSO and DLSR-FS.

	FS	ReliefF	LASSO	DLSR-FS	OLB-CMI
SEMEION	71.99 ± 1.28	75.05 ± 1.89	75.50 ± 2.86	83.43 ± 1.53	85.39 ± 1.42
ISOLET	70.57 ± 0.86	73.30 ± 0.94	76.81 ± 1.33	86.20 ± 0.88	90.31 ± 1.21
ARCENE	59.25 ± 3.70	72.88 ± 5.03	70.63 ± 4.00	71.00 ± 4.10	78.50 ± 3.25
GISETTE	54.24 ± 2.03	84.41 ± 2.83	94.49 ± 0.59	96.30 ± 0.54	95.85 ± 3.47
LUNG	88.17 ± 2.12	92.68 ± 2.50	93.29 ± 2.63	93.17 ± 1.98	94.51 ± 2.36
TOX-171	72.03 ± 5.90	76.96 ± 7.87	67.83 ± 5.29	75.65 ± 1.30	75.94 ± 5.11
WebKB-WT	86.60 ± 3.54	89.68 ± 1.81	90.99 ± 1.28	89.64 ± 2.80	91.11 ± 1.17
WebKB-WC	79.26 ± 1.11	87.77 ± 1.44	88.57 ± 1.44	88.99 ± 1.49	89.79 ± 0.90
UMIST	81.61 ± 6.79	83.91 ± 2.38	95.39 ± 1.50	96.78 ± 1.17	98.17 ± 0.93
AR	41.49 ± 7.95	46.24 ± 5.15	76.88 ± 3.31	84.66 ± 1.93	86.44 ± 1.84
ORL	35.69 ± 6.75	42.00 ± 10.42	71.06 ± 5.56	76.25 ± 4.70	88.44 ± 2.81
CMU-PIE	71.87 ± 5.26	71.58 ± 2.71	80.17 ± 2.21	90.05 ± 1.07	92.18 ± 0.91

Table 7.

Mean and standard deviation of the classification rates (%) of classifiers built on the top 80 features selected by OLB-CMI, FS, ReliefF, LASSO and DLSR-FS.

	FS	ReliefF	LASSO	DLSR-FS	OLB-CMI
SEMEION	85.45 ± 1.11	84.86 ± 0.98	86.27 ± 1.38	89.11 ± 1.26	89.59 ± 1.07
ISOLET	84.18 ± 0.66	84.95 ± 0.74	89.10 ± 1.14	93.85 ± 0.35	94.23 ± 0.37
ARCENE	66.38 ± 2.98	76.75 ± 3.63	73.50 ± 4.06	75.50 ± 5.33	80.25 ± 4.28
GISETTE	93.27 ± 2.88	84.44 ± 1.18	94.90 ± 0.40	97.44 ± 0.68	97.14 ± 0.45
LUNG	92.68 ± 1.81	93.41 ± 1.83	93.90 ± 2.78	94.27 ± 1.64	94.88 ± 2.03
TOX-171	74.49 ± 3.56	80.72 ± 6.54	75.22 ± 6.68	82.61 ± 4.24	82.75 ± 4.82
WebKB-WT	87.84 ± 1.72	91.11 ± 1.08	90.49 ± 1.47	90.13 ± 1.11	90.86 ± 0.78
WebKB-WC	85.74 ± 1.38	88.26 ± 1.45	87.58 ± 1.91	88.76 ± 1.77	90.02 ± 0.83
UMIST	92.39 ± 2.83	88.91 ± 2.80	97.48 ± 1.53	98.13 ± 1.25	98.52 ± 1.09
AR	59.08 ± 8.23	68.68 ± 3.71	88.60 ± 1.99	92.89 ± 0.93	93.97 ± 1.82
ORL	48.31 ± 9.96	55.75 ± 10.19	79.50 ± 3.80	84.63 ± 2.81	92.19 ± 2.74
CMU-PIE	82.04 ± 2.62	79.98 ± 1.48	87.45 ± 1.47	92.18 ± 0.93	93.25 ± 0.62

As shown in Fig. 4, OLB-CMI achieved overall better classification accuracy on almost all the datasets with different numbers of the selected features, except for LUNG and TOX-171 that have relatively smaller number of data samples. For the classifiers built upon the top 40 and 80 selected features, as shown in Table 4 and Table 5, the performance of our method was overall better than other mutual information based methods. Particularly, on SEMION, ISOLET, GISETTE, ARCENE and CMU-PIE, OLB-CMI achieved much better performance than alternative methods.

As shown in Fig. 5, OLB-CMI had better performance than FS and ReliefF with a large margin. Our method had slightly lower accuracy than ReliefF on WebKB-WT. The results shown in Table 6 and Table 7 demonstrated that the classification accuracy of our method was better than FS and ReliefF on most of the datasets. The results shown in Fig. 5 as well as in Tables 6 and 7 also demonstrated that OLB-CMI had better performance than LASSO and DLSR-FS on most datasets with different numbers of the selected features. However, DLSR-FS had better performance than our method on GISETTE. Overall, our method achieved competitive classification accuracy.

In summary, on the 12 datasets, these classification results clearly demonstrated that OLB-CMI had an overall better performance than other 7 feature selection methods, including 3 mutual information based feature selection methods, 2 filter methods, and 2 sparsity regularization based feature selection methods.

In addition, as shown in Fig. 4, Table 4 and Table 5, OLB-CMI had overall better performance than JMI and mRMR that performed better than MIM. The performance ranking of these methods was consistent with the order of strength of the assumptions adopted in these methods. Interestingly, JMI and mRMR were built on assumptions with similar strength, and they had similar performance too. These results also provided evidence to support the principle of Occam’s Razor that the weaker assumptions adopted in a method, the better performance the method will have.

6.3. Running time comparison on real-world datasets

Since LASSO was implemented in C, and other algorithms were implemented in Matlab. Therefore we did not compare LASSO with other methods with respect to their computational costs. In the experiments, the stop conditions of all the feature selection algorithms were following. MIM, JMI, mRMR, and OLB-CMI (α = 0) run until top 100 features were selected; FS and ReliefF run until all features were ranked; DLSR-FS run until the change of its objective function value was less than 10⁻⁴ between 2 successive iteration steps or the iterative counter was more than 1000 with the regularized parameter μ = 1. We run all the methods on a desktop PC with an Intel i7-3770 3.4 GHz CPU and 8 G RAM.

Running time taken by different methods on the 12 widely-used datasets is summarized in Table 8. As shown in Table 8, MIM had the lowest computational cost among all the methods under comparison, FS and MIM had similar computational costs, and ReliefF had moderate computational cost. However, OLB-CMI was computationally expensive compared with other mutual information based feature selection methods. It is worth noting that the time taken by DLSR-FS fluctuated dramatically on different datasets. Since DLSR-FS needs to solve a least-square minimization problem whose computational complexity is O (N²D) at each iteration step, DLSR-FS is more suitable for datasets with a small number of samples.

Table 8.

Running time(unit: second) taken by different Algorithms.

	MIM	JMI	mRMR	FS	ReliefF	DLSR-FS	OLB-CMI
SEMEION	0.04	4.75	3.21	0.14	3.65	22.63	6.87
ISOLET	0.53	67.87	46.51	1.01	320.12	2954.07	106.49
ARCENE	0.68	102.83	85.80	0.67	4.16	0.89	193.85
GISETTE	3.91	480.50	381.91	1.13	621.04	2169.17	894.09
LUGN	0.24	37.85	28.11	1.06	1.66	0.27	65.16
TOX-171	0.42	58.65	47.05	1.36	1.93	0.82	106.97
WebKB-WT	0.52	78.07	56.99	1.50	33.88	4.03	142.58
WebKB-WC	0.65	80.58	56.36	1.43	35.76	5.57	147.75
UMIST	0.23	61.95	26.89	2.98	6.35	0.70	63.57
AR	0.34	199.08	32.25	13.26	47.70	3.82	85.94
ORL	0.99	386.22	100.80	24.31	18.78	1.91	256.51
CMU-PIE	0.63	269.37	64.56	16.04	80.14	20.40	176.96

7. Discussion and conclusions

Information theory based feature selection methods have achieved promising performance for high-dimensional classification problems for its computational efficiency. However, the mechanism behind their success is not well understood. In the present study, a new relationship between Bayesian error rate and the mutual information between features and their class label is discovered, and a unified framework is proposed to bring together information theory based feature selection methods. Under this unified framework, several successful algorithms, including MIM, JMI and mRMR, can be derived as special cases that optimize computationally feasible approximations of high-dimensional conditional mutual information between selected features and their associated label under different assumptions.

A new feature selected method, referred to as OLB-CMI, was developed within the unified framework based on a relatively weaker assumption to estimate conditional mutual information. OLB-CMI could integrate a plug-in component to distinguish redundant from irrelevant features, which makes the feature selection more robust. A new metric, Feature Selection Precision, was developed to directly access the precision of feature selection. The evaluation result demonstrated that OLB-CMI performed better than alternative feature selection methods with respect to Feature Selection Precision. Moreover, OLB-CMI achieved overall better classification performance than alterative information theory based feature selection algorithms on 12 benchmark datasets. Additionally, OLB-CMI achieved similar classification performance as LASSO and DLSR.

Our method could be further improved by developing a method to adaptively set threshold parameter α in the plug-in component that has to be tuned empirically in the present study.

Appendix

A. Proof of Proposition 1

Proof

If Assumption 1 and Assumption 2 are satisfied, we have

$$\begin{gathered} I({\mathit{X}}_{\mathit{S}};C)=\int p({\mathit{x}}_{\mathit{s}},c)\text{log}\frac{p({\mathit{x}}_{\mathit{s}},c)}{p({\mathit{x}}_{\mathit{s}})p(c)}\mathrm{d}{\mathit{x}}_{\mathit{s}}dc \\ =\int p({\mathit{x}}_{\mathit{s}},c)\text{log}\frac{{\prod }_{x_k\in {\mathit{x}}_{\mathit{s}}}p(x_k\mid c)}{{\prod }_{x_k\in {\mathit{x}}_{\mathit{s}}}p(x_k)}\mathrm{d}{\mathit{x}}_{\mathit{s}}dc \\ =\int p({\mathit{x}}_{\mathit{s}},c)\sum log\frac{p(x_k\mid c)}{p(x_k)}\mathrm{d}{\mathit{x}}_{\mathit{s}}dc \\ =\int p({\mathit{x}}_{\mathit{s}},c)\sum log\frac{p(x_k,c)}{p(x_k)p(c)}\mathrm{d}{\mathit{x}}_{\mathit{s}}dc \\ =\sum I(X_k;C). \end{gathered}$$ (A.1)

So, MI between the selected features and their label is equal to the sum of MI between each individual feature and the class label. Therefore, selecting features according to their ranks of individual MI is equivalent to maximizing MI between the selected features and the class label.

B. Proof of Proposition 2

Proof

The optimization problem of maximization of CMI Eq. (5) can be equivalently formulated as

$$X_{\ast }=\underset{X_k\in {\mathit{X}}_{\overline{\mathit{S}}}}{\text{argmax}}(I(X_k;c)+I({\mathit{X}}_{{\mathit{S}}^d};X_k\mid C)-I({\mathit{X}}_{{\mathit{S}}^d};X_k)).$$ (A.2)

For any feature X_i in the selected feature set X_S, we have

$$I({\mathit{X}}_{\mathit{S}};X_k)-I(X_i;X_k)=I({\mathit{X}}_{\mathit{S}/i};X_k\mid X_i)\ge 0.$$ (A.3)

If Assumption 3 is satisfied, the equality will hold, i.e.,

$$I\left({\mathit{X}}_{\mathit{S}/i};X_k\mid X_i\right)=0.$$ (A.4)

Then, we obtain

$$I(X_i;X_k)=I({\mathit{X}}_{\mathit{S}};X_k).$$ (A.5)

And, it indicates

$$\frac{1}{d}\sum _{X_i\in {\mathit{X}}_{\mathit{S}}}I(X_i;X_k)=I({\mathit{X}}_{\mathit{S}};X_k).$$ (A.6)

Meanwhile, if Assumption 4 is satisfied, we have

$$I({\mathit{X}}_{\mathit{S}};X_k\mid C)-I(X_i,X_k\mid C)=I(X_i,X_k\mid {\mathit{X}}_{\mathit{S}/i},C)=0.$$ (A.7)

JMI is also equivalent to

$$X_{\ast }=\underset{X_k\in {\mathit{X}}_{\overline{\mathit{S}}}}{\text{argmax}}\left(I(X_k;C)+\frac{1}{d}\sum _{X_i\in {\mathit{X}}_{\mathit{S}}}I(X_i,X_k\mid C)-\frac{1}{d}\sum _{X_i\in {\mathit{X}}_{\mathit{S}}}I(X_i;X_k)\right).$$ (A.8)

Therefore, if Assumption 3 and Assumption 4 are satisfied, JMI is equivalent to Eq. (A.2) and Eq. (5).

C. Proof of Proposition 3

Proof

According to the proof of Proposition 2, if Assumption 3 is satisfied, we have

$$\frac{1}{d}\sum _{X_i\in {\mathit{X}}_{\mathit{S}}}I(X_i;X_k)=I({\mathit{X}}_{\mathit{S}};X_k).$$ (A.9)

If Assumption 5 is satisfied, then

$$I({\mathit{X}}_{\mathit{S}};X_k\mid C)=0.$$ (A.10)

Recalling mRMR:

$$X_{\ast }=\underset{X_k\in {\mathit{X}}_{\overline{S}}}{\text{argmax}}\left(I(X_k;C)-\frac{1}{d}\sum _{X_i\in {\mathit{X}}_{\mathit{S}}}I(X_i;X_k)\right).$$ (A.11)

Therefore, if Assumption 3 and Assumption 5 are satisfied, mRMR is equivalent to Eq. (A.2) and Eq. (5).

D. Proof of Proposition 4

Proof

The optimization problem of Eq. (5) is equivalent to

$$X_{\ast }=\underset{X_k\in {\overline{\mathit{X}}}_{\mathit{S}}}{\text{argmax}}(I({\mathit{X}}_{{\mathit{S}}^d},C;X_k)-I({\mathit{X}}_{{\mathit{S}}^d};X_k)).$$ (A.12)

If Assumption 3 is satisfied, for any of the selected features X_i and any of the unselected features X_k, we have

$$I({\mathit{X}}_{\mathit{S}};X_k)-I(X_i;X_k)=I({\mathit{X}}_{\mathit{S}/i};X_k\mid X_i)=0.$$ (A.13)

Therefore

$$I({\mathit{X}}_{\mathit{S}};X_k)=I(X_i;X_k).$$ (A.14)

Since any conditional mutual information is greater or equal to zero,

$$I({\mathit{X}}_{\mathit{S}},C;X_k)-I(X_i,C;X_k)=I({\mathit{X}}_{\mathit{S}/i};X_k\mid X_i,C)\ge 0.$$ (A.15)

Thus,

$$I(X_i,C;X_k)\le I({\mathit{X}}_{\mathit{S}},C;X_k).$$ (A.16)

Combining Eq. (A.14) and Eq. (A.16), we have

$$I(X_i,C;X_k)-I(X_i;X_k)\le I({\mathit{X}}_{\mathit{S}},C;X_k)-I({\mathit{X}}_{\mathit{S}};X_k).$$ (A.17)

Therefore, $\underset{X_i\in {\mathit{X}}_{\mathit{S}}}{max}I(X_i,C;X_k)-I(X_{i\ast };X_k)$ is a tight lower bound of I (X_k; C|X_S^d).